具有维护活动及公共工期的加工时间依赖资源的单机排序问题
隋 楠,罗成新
(沈阳师范大学 数学与系统科学学院,沈阳 110034)
具有维护活动及公共工期的加工时间依赖资源的单机排序问题
隋 楠,罗成新
(沈阳师范大学 数学与系统科学学院,沈阳 110034)
研究在工件的提前惩罚、延误惩罚等总费用受限的前提下,最小化资源费用的单机排序问题。所有工件具有一个公共工期,工件的加工时间是关于位置与资源的具有退化效应的凸函数。在加工过程中,存在一次维护活动。考虑维护活动对依赖于资源的加工时间的影响,确定最优资源分配、最优公共工期、最优维护位置及维护持续时间,并给出一个求得最小资源费用的多项式时间最优算法。
排序;维护活动;工期;资源分配;退化效应
排序问题是一类重要的组合最优化问题,多年来人们一直在运筹学、计算机科学、管理科学等领域进行着该问题的研究。在经典排序模型中,工件的加工时间是一个独立的且与加工位置和资源无关的常数,但在实际问题中,工件的加工时间可能会在机器的维护作用下相应缩短,或者通过适当地分配给工件一定的资源,使其加工效率提高,加工时间缩短。
近20年,由于现代运营管理等产业的引进,具有公共工期的排序问题陆续进入人们的视野。如果一个工件在它的工期之前完成加工,那么它需要承担一部分的提前惩罚费用,相应的,如果一个工件在它的工期之后完成加工,那么它需要承担一部分的延误惩罚费用。文献[6]首先研究了带有公共工期的排序问题,目标是最小化提前惩罚、延误惩罚和工期的总费用。自此之后,在不同环境下的带有公共工期的排序问题被陆续研究着。
文献[4]首先研究了带有退化效应的排序问题。由于实际生产的需要,维护问题越来越受重视。为了更好地提高机器的运行效率,需要对机器进行维护,使机器恢复到初始状态或者提高机器的生产效率,文献[13]研究了具有固定维护时间的单机排序问题,给出了多项式算法。在研究具有维护活动的排序问题中,维护活动持续的时间都是固定的常数,但在实际生产过程中,维护活动持续的时间受到多种因素影响,通常假定为关于维护活动开始时间的线性函数。文献[2]和[5]研究了具有公共工期和维护活动的单机排序问题。
经典排序模型中,任务的加工时间通常都是固定的常数,然而考虑到学习效应、退化效应、资源分配等情况,任务的加工时间不再是固定不变的。文献[7]和[8]研究了不同环境下的具有维护活动的单机排序问题。由于实际生产活动的需要,带有资源分配的问题逐渐引起关注,文献[3]、[10]和[11]研究了关于资源分配的单机排序问题。
在大多排序模型中,往往以最小化所需费用为首要目标。但实际生产过程中,有时即便使得总费用最小,也不能满足生产者对费用的预估最小值。因此生产者常常会事先给定预算以限制总费用。文献[11]研究了多种工期下资源受限的单机排序问题,并给出了在总费用受限的前提下资源总数的最优算法。因此,本文在文献[11]的基础上,研究了带有公共工期和维护活动的总费用受限的单机排序问题,工件的加工时间是关于位置与资源的具有退化效应的凸函数,并给出了最优算法,该算法通过求解指派问题在O(n4)时间内求得最优资源分配、最优公共工期、最优维护位置及维护持续时间及最小资源费用。
1 问题(1)描述
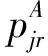
(1)在维修活动之后,机器恢复到初始状态,退化影响也重新计算;
(2)机器维修的持续时间是关于开始时间的线性函数,表示为f(t)=x+yt,其中x>0,y≥0为常数,分别为基本维护时间和维护退化因子,t为维修开始时间;
(3)i为维修活动前的最后一个工件,即维修活动后的第一个工件表示为i+1,其中i∈{1,2,…,n}。
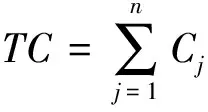
其中α>0、β>0、γ>0、θ≥0、δ≥0为给定常数,vj(>0)为资源分配的单位费用。用三参数表示法[9]如式(1)所示。
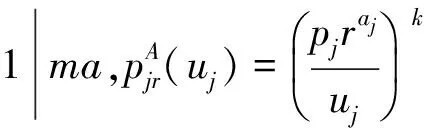
(1)
其中Q>max{nx(γ+max{α,δ}),(β+δ)nx}为已知常数。
2 问题的最优解
2.1 重要结论
引理1 存在最优排序,任务开始加工时间为0,且两个相邻工件之间无空闲时间。
证明 详细证明见参考文献[6]。
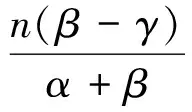
证明 详细证明与参考文献[2]中证明类似。证毕。


2.2 最优算法
若维修活动在工期前,即当1≤i≤m时:
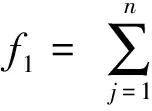
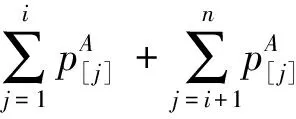
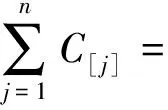
从而

(2)
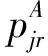
(3)
j=1,2,…,n
(4)
其中
(5)
(6)
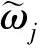
对于任意给定排序,拉格朗日函数如式(7)所示。
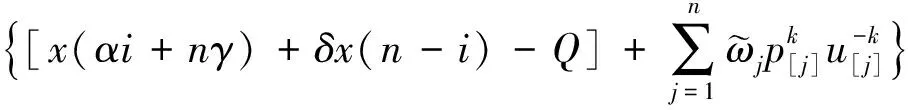
(7)
其中λ为拉格朗日乘数。对(7)式中的变量分别求偏导,如式(8)和式(9)所示。

(8)
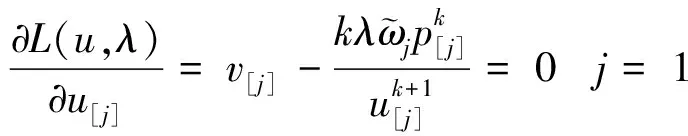
(9)
由式(8)和式(9)可得
(10)
(11)
由式(10)和式(11)可得式(4),证毕。

(12)

为了求出式(12)的最小值,考虑指派问题如下:
则问题转化为如下指派问题:
(13)
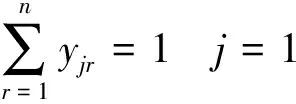
(14)
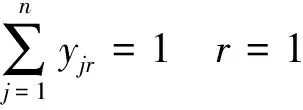
(15)
yjr=1或0 j,r=1,2,…,n
(16)

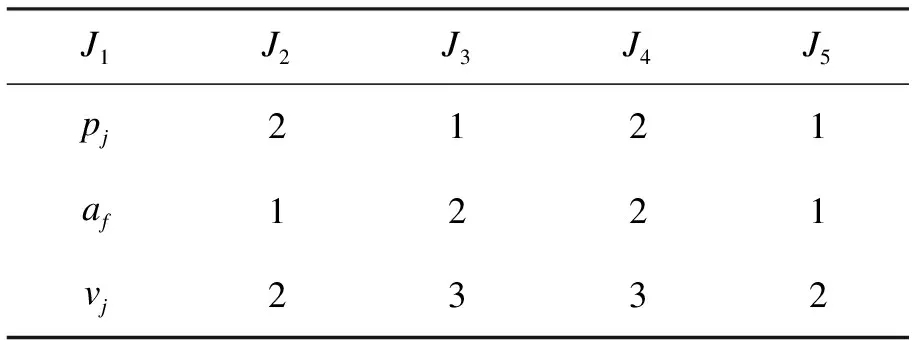
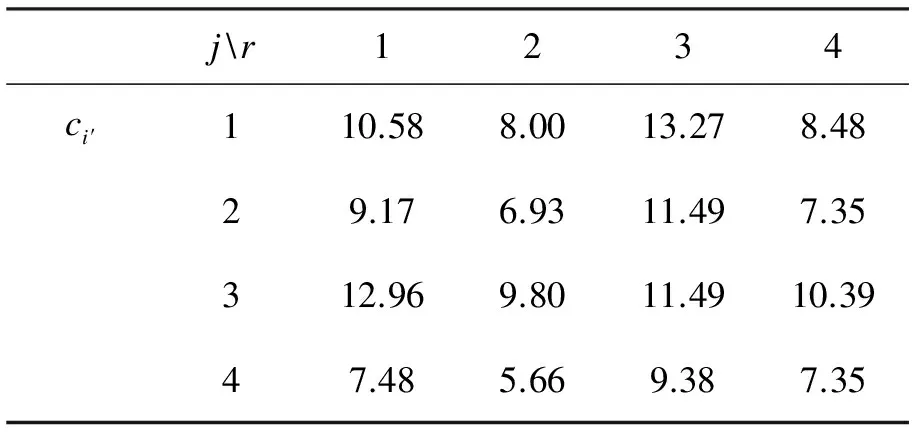
若维修活动在工期后,即当m 此时,可以得到约束条件如下: (17) j=1,2,…,n (18) 其中 (19) 对于任意给定排序,拉格朗日函数如式(20)所示。 (20) 其中λ为拉格朗日乘数。对式(20)中的变量分别求偏导,得到 (21) (22) 由式(21)和式(22)可得 (23) (24) 由式(23)和式(24)可得式(18),证毕。 Z(π,d,u*) (25) 为了求出式(25)的最小值,考虑指派问题如下: 则问题转化为如下指派问题: (26) (27) (28) yjr=1或0 j,r=1,2,…,n (29) 证明 每个指派问题可以在O(n3)时间内求得最优解,而维修的位置可取1,2,…,n,共n种情况,结论得证。 表1 例1的数据 表2 例1中ci′值 本文研究了具有维护活动及公共工期,且加工时间依赖于资源的单机排序问题。加工时间是关于资源的凸函数,维护活动有且仅有一次,在部分总费用受限的前提下,给出了一个最优算法求解最优资源费用、最优资源分配及最优工期。 [1]CHENG T C E.Optimal single machine sequencing and assignment of common due-date[J].Computers and Industrial Engineering,1992,22:115-120. [2]YANG S J,HSU C J,YANG D L.Single-machine scheduling with due-date assignment and aging effect under a deteriorating maintenance activity consideration[J].International Journal of Information and Management Sciences,2010,21:177-195. [3]LU Y Y,LI G,WU B P.JI.Optimal due-date assignment problem with learning effect and resource-dependent processing times[J].Optimization Letters 2014,8(1):113-127. [4]LEE W C.A note on deteriorating jobs and learning in single machine scheduling problems[J].Int J Business Econ,2004,3(1):83-89. [5]MOSHEIOV G,ORON D.Due-date assignment and maintenance activity scheduling problem[J].Mathematical and Computer Modeling,2006,44(11-12):1053-1057. [6]PANWALKAR S S,SMITH M L,SEIDMANN A.Common due date assignment to minimize total penalty for the one machine scheduling problem[J].Operations Research,1982,30(2):391-399. [7]YAO M J,HUANG J Y.A global-optimization algorithm for solving the maintenance scheduling problem for a family of machines[J].International Journal of Information and Management Sciences,2007,18(4):365-386. [8]MOSHEIOV G,SARIG A.Scheduling a maintenance activity to minimize total weighted completion time[J].Computer and Mathematics with Application,2009,57:619-623. [9]GRAHAM R L,LAWLER E L,LENSTRA J K,et al.Optimization and approximation in deterministic sequencing and scheduling[J].A survey,Annals of Discrete Mathematics,1979,5(1):287-326. [10]WANG X Y,WANG J J.Single-machine due-date assignment problem with deteriorating jobs and resource-dependent processing times[J].International Journal of Advanced Manufacturing Technology,2013,67(1):255-260. [11]WANG J B,WANG J J.Research on scheduling with job-dependent learning effect and convex resource-dependent processing times[J].International Journal of Production Research,2015,53(19):1-11. [12]MOSHEIOV G,SIDNEY J B.Scheduling a deteriorating maintenance activity on a single machine[J].Journal of the Operational Research Society,2010,61(5):882-887. [13]MPSJEOPV G,SARIG A.Scheduling a maintenance activity and due-window assignment on a single Machine[J].Computers&Operations Research,2009,36(9):2541-2545. [14]WAN G.Single machine common due window scheduling with controllable job processing times[J].Lecture Notes in Computer Science,2007,4616:279-290. [15]王吉波,郭苗苗,刘桓,等.具有依赖开工时间恶化工件的流水作业排序问题研究综述[J].沈阳航空航天大学学报 2016,33(3):1-10. [16]王吉波,刘璐,许扬涛,等.具有恶化工件的不同工期指派问题研究[J].沈 阳航空航天大学学报,2013,30(5):83-87. [17]王吉波,汪佳,牛玉萍.具有学习效应 的单机可控加工时间排序问题研究[J].沈阳航空航天大学学报,2014,31(5):82-86. (责任编辑:刘划 英文审校:刘勇进) Single machine scheduling with job-dependent and maintenance activities and processing time dependent on resources with due-date SUI Nan,LUO Cheng-xin (School of Mathematics and Systems Science,Shenyang Normal University,Shenyang 110034,China) In this paper,we study the single machine scheduling problem of minimizing resource costs under the conditions that the earliness,tardiness and other penalties are limited.All the jobs have a common due-date,and the actual processing times are defined by a convex function of their normal processing times,positions and the effect index of deteriorating and resources.There is a maintenance activity in the processing.Considering the effect on the processing time of resource from maintenance,we give the optimal resource allocation,the optimal due-date,the optimal place for maintenance and the lasting time of maintenance.An optimal polynomial time algorithm for the minimum resource cost is given. scheduling;maintenance activities;due-date;resource allocation;deteriorating effect 2016-10-28 隋 楠(1992-),女,辽宁铁岭人,硕士研究生,主要研究方向:组合最优化与随机运筹学,E-mail:nannan879@126.com。 2095-1248(2016)06-0090-07 O223 A 10.3969/j.issn.2095-1248.2016.06.015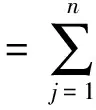
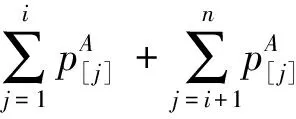
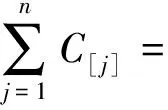
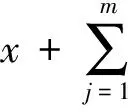
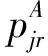
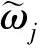
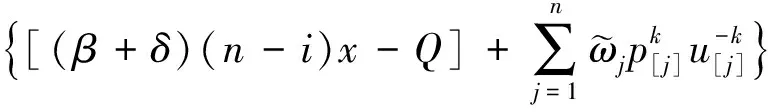

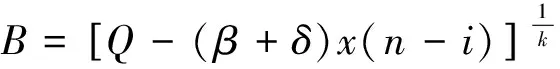
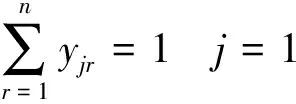
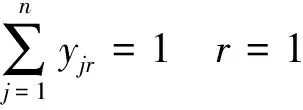

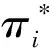

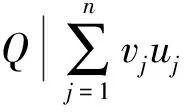

3 结论

