尺度依赖的Reddy型碳纳米管功能梯度板的自由振动模型
贺 丹,门 亮
(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)
尺度依赖的Reddy型碳纳米管功能梯度板的自由振动模型
贺 丹,门 亮
(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)
基于一种新的修正偶应力理论建立了微观尺度下碳纳米管增强型复合材料功能梯度板的自由振动模型。基于三阶剪切理论和哈密顿原理推演了该板模型的运动微分方程及边界条件,并以四边简支方板为例给出了板自由振动基频的解析解。研究了碳纳米管分布类型、碳纳米管体积分数、板尺寸等参数对板自由振动基频的影响。算例结果表明:模型能够有效地捕捉到尺度效应,且板的尺寸越小尺度效应越明显;碳纳米管的分布形式和碳纳米管体积分数对板基有显著影响。
修正偶应力理论;碳纳米管;功能梯度材料;自由振动;尺度效应
诸多试验[1-3]证实,金属材料、复合材料以及高分子有机材料在微观尺度下表现出比宏观尺度更高的刚度,即尺度效应。传统的连续介质力学无法解释尺度效应,因此人们建立了广义连续介质力学理论,其中主要包括应变梯度理论[4]和偶应力理论[5]。广义连续介质力学理论在本构关系中引入若干个尺度参数用于解释尺度效应,因此能够适用于微观尺度下对材料力学行为的预测,同时也能适用于宏观尺度下对材料性能的描述。
材料尺度参数是材料本身固有的常数,其数值需要依赖于试验进行测定。值得注意的是,对于同一种材料在应变梯度理论和偶应力理论下其尺度参数是不同的[6]。确定材料尺度参数相当困难,很多学者在探索含有较少尺度参数的理论上投入了很多时间和精力,并取得了很多成果。相对于应变梯度理论,Yang等[7]人提出的修正偶应力理论中只含一个尺度参数,非常便于工程应用,基于该理论人们建立了一系列的考虑尺度效应的板、梁模型[8-11],但是,修正偶应力理论只适用于各向同性材料。近年来,陈万吉等[12]提出了一种新的修正偶应力理论,该理论将使微尺度各向同性材料的研究推广到各向异性材料。
碳纳米管具有优异的力学性能,是作为复合材料增强相的优质选择。通过变化碳纳米管分布形式,能够形成具有良好力学性能的碳纳米管增强型复合功能梯度材料(FG-CNTRC)。随着微/纳米机电技术的发展,FG-CNTRC已经作为制造微、纳米级别的传感器、制动器以及显微镜等[13-15]的材料被广泛应用。对于微观尺度下的FG-CNTRC板,通过实验确定它的力学性质非常困难,近年来,通过数值分析模拟的方法[16-19]研究FG-CNTRC板的力学性能引起了越来越多学者的关注。
K.M.Liew等[20]人基于有限元法研究了宏观尺度下FG-CNTRC板弯曲及自由振动。Rokni H[21]和Shahriari B[22]等人基于应变梯度理论分别研究了微观尺度下FG-CNTRC梁和板的自由振动的尺度效应。但是,目前为止,在偶应力理论体系下,对属于各向性异性材料性质的微观尺度下FG-CNTRC板的研究极少。
基于新修正偶应力理论建立了FG-CNTRC板自由振动模型。基于哈密顿原理推导了运动微分方程,并以四边简支方板为例探讨了板尺寸、碳纳米管分布类型和体积分数等参数对FG-CNTRC板自振基频的影响。算例结果表明,本文建立的模型能够解释微观尺度下FG-CNTRC板的尺度效应问题。
1 新修正偶应力理论
新修正偶应力理论由陈万吉等[12]人首次提出。应变εij和曲率χij分别定义如式(1)所示。
(1)
本构关系定义如式(2)所示。
(2)
其中:δij是克罗内克符号,λ和G为Lame常数,u和ω分别为平动位移和转动位移,li是材料尺度参数,εij、σij、χij和mij分别为应变、应力、曲率和偶应力。
2 新修正偶应力理论下FG-CNTRC板模型
2.1 位移方程
采用三阶剪切理论,FG-CNTRC板位移方程[23]如式(3)所示。
(3)

转动位移如式(4)所示。
ωi=1/2eijkuk,j
(4)
由式(3)和(4)得到FG-CNTRC板转动位移方程如式(5)所示。
(5)
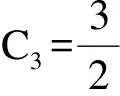
2.2 FG-CNTRC板的应变分量和曲率分量
将式(5)代入式(1)中得到应变分量如式(6)所示。
(6)
将式(5)代入式(1)中得到曲率分量如式(7)所示。
(7)
其中:
2.3 FG-CNTRC板的本构关系
本构关系如式(8)所示。
σ=Qε
(8)
式中σ和ε分别为应力张量和应变张量,如式(9)所示。

(9)

其中:Q11=E11/(1-υ12υ21),Q12=υ21E11/(1-υ12υ21),Q22=E22(1-υ12υ21),Q33=G12,Q44=G13,Q55=G23,Q66=G13,Q77=G23,G12=G13=G23。lb和lm分别为碳纳米管和基体材料的尺度参数。E11和E22为FG-CNTRC板弹性模量,G12、G13、G23为板剪切模量,υ12和υ21为泊松比,由式(10)得到[20]。
(10)

2.4 FG-CNTRC板分布类型
FG-CNTRC板有4种类型[20]:UDCNTRC、FG-VCNTRC、FG-XCNTRC和FG-OCNTRC,如图1所示。

图1 碳纳米管在基体中的分布
碳纳米管沿厚度方向体积分数表达式如式(11)所示。
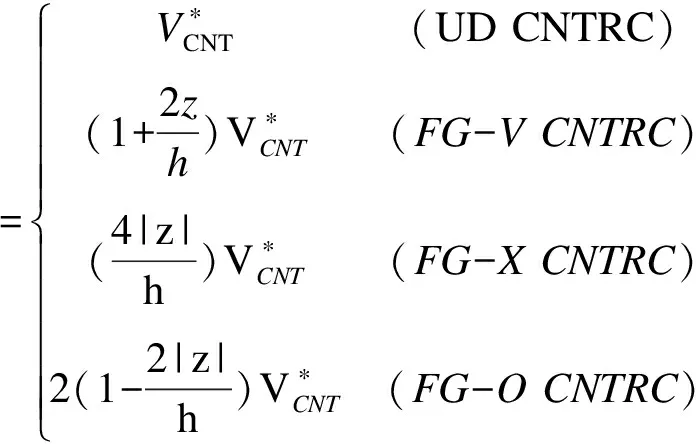
(11)
3 FG-CNTRC板哈密顿原理
哈密顿原理如式(12)所示。

(12)
式中U为应变势能,W为外力做功,T为动能,t1、t2为时间,分别如式(13)-(15)所示。
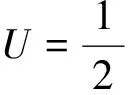
(13)

(14)

(15)
ρ为板的密度如式(16)所示。
ρ=VCNTρCNT+Vmρm
(16)
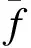
由以上关系可得到FG-CNTRC板的运动微分方程如式(17)所示。
(17)
以及边界条件如式(18)所示。
(18)
其中:
{NxNyNxyNxzNyzMxMyMxyYxYyYxyYyx}T=


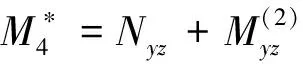
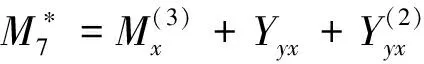

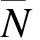
4 FG-CNTRC板的算例分析
本节对四边简支的方板进行自由振动分析。事实上,碳纳米管的尺度参数要远远大于基体的尺度参数lm,为便于工程应用,可近似认为lm=0。
对四边简支的FG-CNTRC板边界条件如式(19)所示。
(19)
满足全部边界条件的位移函数如式(20)所示。
(20)
其中,α=π/a,β=π/b。u00、v00、ψx0、ψy0、w0为待定系数,ω为待求频率。 令全部外界载荷为零,将式(20)代入(17)得到
([K]-ω2[M]){U}=0
(21)
其中:{U}={u00v00ψx0ψy0w0}T,[K]和[M]分别为刚度矩阵和质量矩阵。对式(21)求广义特征值便可得到板自由振动频率。
给定FG-CNTRC板材料常数及碳纳米管的效率参数如表1和表2[20]所示。
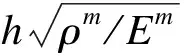
图2~图5分别给出4种分布类型下,碳纳米管体积分数取0.11、0.14和0.17时,本文模型和经典理论下FG-CNTRC板的无量纲自振频率。4个图中present为本文模型的结果,classical为经典理论结果。横坐标为板厚与尺度参数的比值,由于尺度参数固定,比值越大说明板的尺寸越大,纵坐标为无量纲频率。由图2~图5可知,采用本文模型所预测的板自由振动频率总是大于经典理论预测的结果,且板的几何尺寸越小,2种理论之间的差别就越明显,而当板的尺寸足够大时,2种理论的结果趋于一致,说明本文模型能够有效地描述尺度效应带给结构的刚度增强现象;进一步研究发现,碳纳米管的体积分数的变化对板自振频率有显著影响,体积分数越高,板自由振动频率越大。这是由于碳纳米管的弹性模量远远大于基体材料的弹性模量,故而碳纳米管能够增加结构的刚度,且体积分数越高,对结构刚度增强越明显;另外,对比图2~图5可知,碳纳米管的分布形式对板的自振频率有直接影响。在本文给定的几种分布类型中FG-X分布板自由振动基频最大,这是因为FG-X型分布方式在板的上下表面碳纳米管的密度较大,使碳纳米管对结构的刚度起主要作用,从而使板的刚度大于其他几种分布类型。这与实际工程上工字型梁具有较大的刚度的现象相一致。
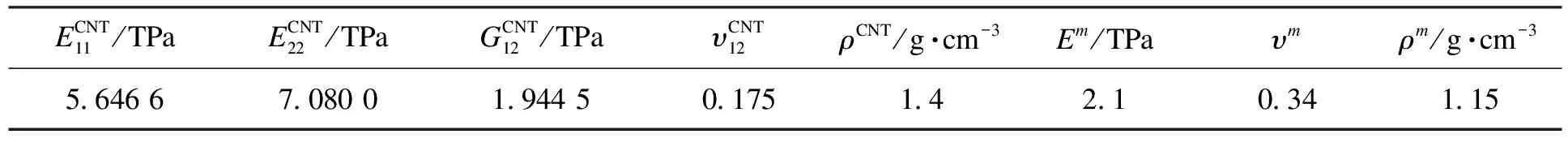
表1 FG-CNTRC板的材料常数

表2 碳纳米管的效率参数

图2 UD型分布无量纲频率

图3 FG-V型分布无量纲频率

图4 FG-X型分布无量纲频率
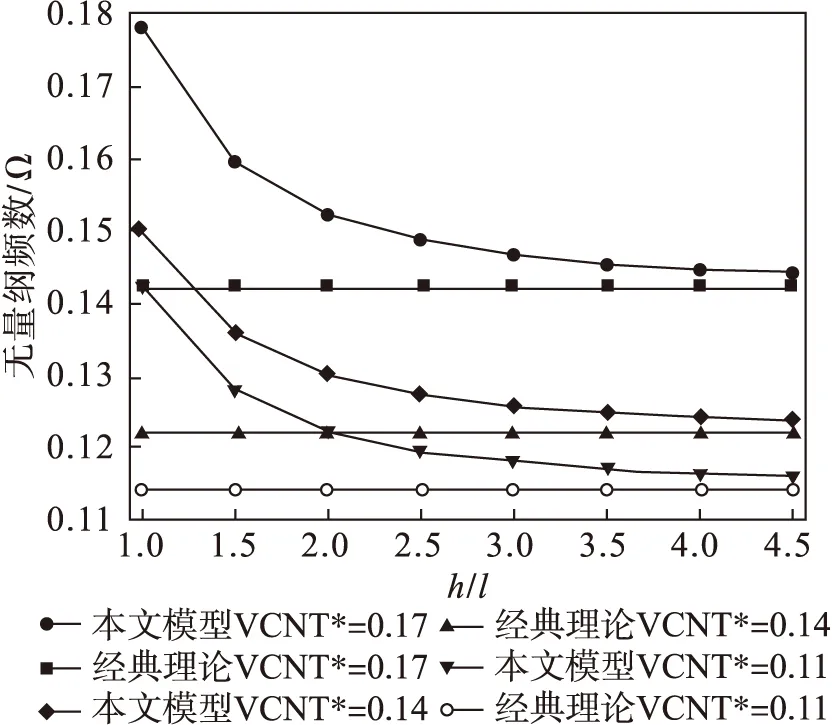
图5 FG-O型分布无量纲频率
5 结论
本文首次将各向异性的新修正偶应力理论应用到考虑横向三阶剪切变形的FG-CNTRC板模型中,建立了微观尺度下各向异性FG-CNTRC板的本构方程,基于哈密顿原理推导了板的运动微分方程及边界条件,并以四边简支方板为例给出了不同碳纳米管分布类型、碳纳米管体积分数、板尺寸等参数下板自振频率的解析解。算例结果表明:本文模型能够有效地捕捉到微观尺度下板的尺度效应,且板的尺寸越小,尺度效应越明显;碳纳米管体积分数的增加能够提高结构的刚度,从而使板自振频率增大;碳纳米管分布形式对板的刚度有直接影响。在本文研究的4种分布类型FG-CNTRC板中,FG-X型分布刚度最大,其次为UD型分布,FG-O型分布刚度最小。
[1]STOLKEN J S,EVANS A G.A microbend test method for measuring the plasticity length scale[J].Acta Materialia,1998,46(14):5109-5115.
[2]ZHAO M,SLAUGHER W S,LI M,et al.Material-length-scale-controlled nanoindentation size effects due to strain-gradient plasticity[J].Acta Materialia,2003,51(15):4461-4469.
[3]FLECK N A,MULLER G M,ASHBY M F,et al.Strain gradient plasticity:theory and experiment[J].Acta Metallurgica Et Materialia,1994,42(2):475-487.
[4]FLECKl N A,HUTCHINSON J W.Strain gradient plasticity[J].Advances in Applied Mechanics,1997,33(12):295-361.
[5]TOUPIN R A.Theories of elasticity with couplestress[J].Archive for Rational Mechanics & Analysis,1963,17(2):85-112.
[6]BIN J,WANJI C.On the nonlocal theory of microstructures and it′s implementation of finite element methods[J].Recent Patents on Engineering,2010,4(8):63-72.
[7]YANG F,CHONG A C M,LAM D C C,et al.Couple stress based strain gradient theory for elasticity[J].International Journal of Solids & Structures,2002,39(10):2731-2743.
[8]MA H M,GAO X L,REDDY J N.A non-classical mindlin plate model based on a modified couple stress theory[J].Acta Mechanica,2011,220(1):217-235.
[9]MA H M,GAO X L,REDDY J N.A nonclassical reddy-levinson beam model based on a modified couple stress theory[J].International Journal for Multiscale Computational Engineering,2010,8(6):167-180.
[10]PARK S K,GAO X L.BernoulliEuler beam model based on a modified couple stress theory[J].Journal of Micromechanics & Microengineering,2006,114(11):332-341.
[11]YIN L,QIAN Q,WANG L,et al.Vibration analysis of microscale plates based on modified couple stress theory [J].Acta Mechanica Solida Sinica,2010,23(5):386-393.
[12]CHEN W,LI L,XU M.A modified couple stress model for bending analysis of composite laminated beams with first order shear deformation [J].Composite Structures,2011,93(11):2723-2732.
[13]WANG W L,HU S J.Modal response and frequency shift of the cantilever in a noncontact atomic force microscope[J].Applied Physics Letters,2005,87(18):183506.
[14]RAHAEIFARD M,KAHROBAIYAN M H,AHMADIAN M T.Sensitivity analysis of atomic force microscope cantilever made of functionally graded materials[C].ASME 2009.International Design Engineering Technical Conferences and Computers and Information in Engineering Conference,2009,94(4):145-156.
[15]LI C,THOSTRNSON E T,CHOU T W.Sensors and actuators based on carbon nanotubes and their composites:A review[J].Composites Science & Technology,2008,68(6):1227-1249.
[16]YAS M H,SAMADI N.Free vibrations and buckling analysis of carbon nanotube-reinforced composite timoshenko beams on elastic foundation[J].International Journal of Pressure Vessels & Piping,2012,98(10):119-128.
[17]LEI Z X,LIEW K M,YU J L.Large deflection analysis of functionally graded carbon nanotube-reinforced composite plates by the element-free kp-Ritz method[J].Computer Methods in Applied Mechanics & Engineering,2013,256(2):189-199.
[18]SHEN H S.Nonlinear bending of functionally graded carbon nanotube-reinforced composite plates in thermal environments[J].Composite Structures,2009,91(1):9-19.
[19]SHAHRBABAKI E A,ALIBEIGLOO A.Three-dimensional free vibration of carbon nanotube-reinforced composite plates with various boundary conditions using ritz method[J].Composite Structures,2014,111(11):362-370.
[20]ZHU P,LEI Z X,LIEW K M.Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory[J].Composite Structures,2012,94(4):1450-1460.
[21]ROKN H,MILANI A S,SEETHALER R J.Size-dependent vibration behavior of functionally graded CNT-Reinforced polymer microcantilevers:modeling and optimization[J].European Journal of Mechanics-A/Solids,2015,49(6):26-34.
[22]SHAHRIARI B,RAVARI M R K,ZEIGHAMPOUR H.Vibration analysis of functionally graded carbon nanotube-reinforced composite nanoplates using mindlin’s strain gradient theory[J].Composite Structures,2015,134:1036-1043.
[23]REDDY J N.Mechanics of laminated composite plates and shells:theory and analysis[M].Boca Raton,FL CRC Press,2004,37(5):25-33.
[24]KE L L,WANG Y S.Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory[J].Composite Structures,2011,93(2):342-350.
(责任编辑:刘划 英文审校:赵欢)
A size-dependent free vibration model of carbon nanotubes functionally graded Reddy plates
HE Dan,MEN Liang
(Key Laboratory of Liaoning Province for Composite Structural Analysis of Aerocraft and Simulation,Shenyang Aerospace University,Shenyang 110136,China)
A free vibration model of anisotropic functionally graded carbon nanotube reinforced composite plate was established based on the new modified couple stress theory.The motion differential equations and boundary conditions were derived based on the third-order shear deformation theory and Hamiton principle.A simply supported plate was taken to be an illustrative example and analytical solution.The effects of distributions,volume fraction of the carbon nanotubes and size of the plate on fundamental frequencies of free vibration were investigated.Numerical results show that the present model can effectively capture the scale effect.The smaller the geometrical size,the more obvious is the scale effect.The distributions and volume fraction of carbon naotubes have remarkable effects on the fundamental frequencies.
modified couple stress theory;carbon nanotubes;functionally graded materials;free vibration;scale effect
2016-10-28
国家自然科学基金(项目编号:11572204)
贺 丹(1979-),男,辽宁沈阳人,副教授,博士,主要研究方向:微细观复合材料力学、结构优化,E-mail:Danhe@sau.edu.cn。
2095-1248(2016)06-0008-07
O343.8
A
10.3969/j.issn.2095-1248.2016.06.002
航空宇航工程

