基于多路合成的π/4 QPSK的设计与实现

刘志鹏，孙延坤，刘轶铭，王兆伟

(中国电子科学研究院，北京 100041)



基础理论

基于多路合成的π/4 QPSK的设计与实现

刘志鹏，孙延坤，刘轶铭，王兆伟

(中国电子科学研究院，北京 100041)

研究了π/4 QPSK的调制解调.为了达到DAC的采样率，采用了多路合成得到π/4 QPSK.给出了基于查表的平方根升余弦成形滤波器的设计方法；对比了直接采用平方根升余弦成形滤波器得到的π/4 QPSK的频谱和基于查表的平方根升余弦成形滤波器得到的π/4 QPSK的频谱，分析得到直接采用平方根升余弦成形滤波器得到的π/4 QPSK的频谱会产生不需要的频谱分量.在多路合成时，需要采用基于查表的平方根升余弦成形滤波器的设计方法.分析了中频差分解调方法，得到理论误码率曲线和仿真结果基本一致。

π/4 QPSK；升余弦滤波器；多路合成

0 引 言

QPSK能够达到与BPSK相同的误码率，但是传输了2倍的信息。QPSK不仅利用了幅度信息还利用了相位信息，而BPSK只利用了幅度信息，故QPSK的误码率与BPSK相当，但是信息速率却比BPSK高的原因[1-2]。π/4 QPSK相对于普通的QPSK而言，能够有效减少相位突变量，功率谱的旁瓣相对更低。以往的文献[3]中多数是给出了单路的π/4 QPSK的实现方法，但是随着随着技术的发展，DAC的采样频率越来越高，而FPGA芯片的时钟速度却没有达到DAC的采样频率。为了克服这一问题，在进行π/4 QPSK设计时一般采用多路合成的方式来进行。例如，DAC的采样频率为800 MHz，显然目前的FPGA芯片无法达到这么高的速率，故一般分成四路合成，每一路为200 MHz，然后在送给DAC之前，将一、三路合并为一路，二、四合并为一路，并采用双边沿(DDR)的方式，达到800 MHz的采样频率。本文将给出基于多路合成的π/4 QPSK设计方法。

为了使π/4 QPSK带外的辐射电平能够达到要求，需要对功率谱的旁瓣进行抑制。一般采用升余弦滤波器进行抑制。由于为了达到DAC较高的采样频率，对信息进行升余弦滤波器时，同样需要多路合成的问题。本文给出了基于查表的平方根升余弦成形滤波器的设计方法。

最后本文给出了π/4 QPSK中频差分解调方法，并对误码率进行了仿真。

1 π/4 QPSK数学原理

1.1 π/4 QPSK基本原理

π/4 QPSK是的一种基于差分编码的QPSK信号。如果不考虑噪声的影响，π/4 QPSK信号的数学表达式为[4-5]

sk(t)=cos(2·π·fc·t+φk)=

cos(φk)·cos(2·π·fc·t)-sin(φk)·

cos(2·π·fc·t)=

cos(φk-1+Δφk)·cos(2·π·fc·t)-

sin(φk-1+Δφk)·cos(2·π·fc·t)

(1)

其中k·T≤t<(k+1)·T，fc为载波，Δφk为当前码元信号的相位φk与上一码元信号的相位φk-1之差。

定义

xk=cos(φk-1+Δφk)，yk=sin(φk-1+Δφk)

(2)

根据式(1)可以得到π/4 QPSK调制的基本框图如图1所示。

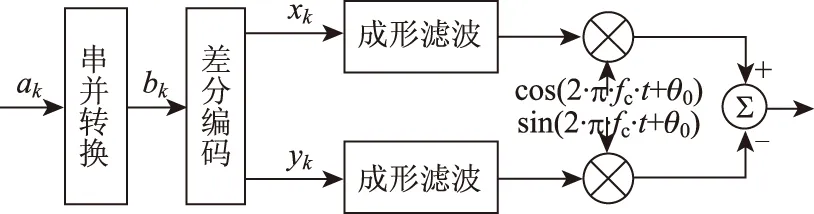
图1 π/4 QPSK调制示意图

码元ak为经过串并转换后得到码元bk，再经过差分编码得到xk和yk，具体的取值如表1所示。

xk和yk分别经过成形滤波后用MATLAB得到的结果如图2和图3所示。

经过中频调制后，I路和Q路相加后得到的结果如图4所示。

表1 码元、相位值与和对应表

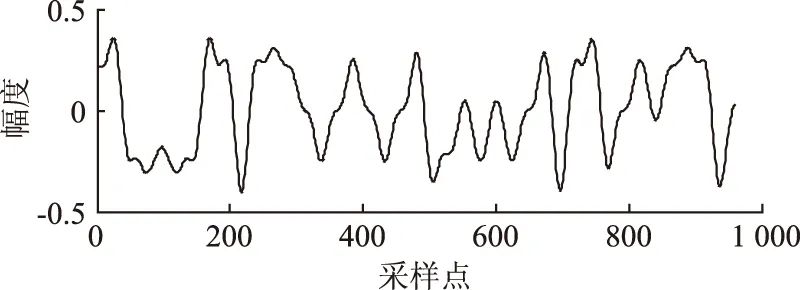
图2 xk经过成形滤波后得到的结果

图3 yk经过成形滤波后得到的结果

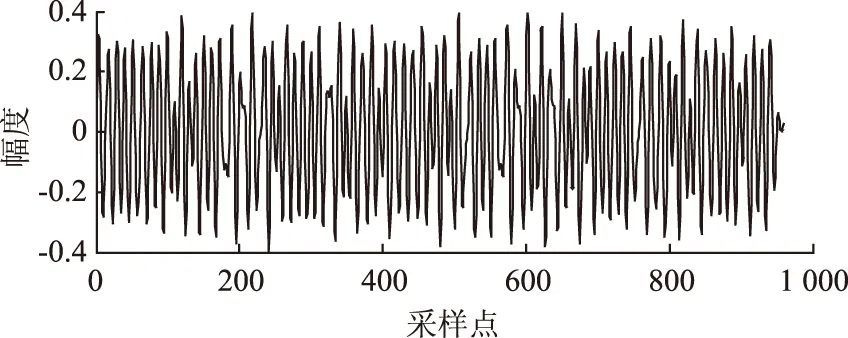
图4 π/4 QPSK调制后的结果

1.2 多路合成

如果采用多路合成时，式的形式还需要进行进一步改变。

sik(t)=xk·cos(2·π·fc·t+θi)-

yk·sin(2·π·fc·t+θi)

(3)

其中

(4)

如果DAC的采样频率为fDAC=800 MHz，采用n=4路来实现，则fs=200 MHz。

类似于单路π/4 QPSK调制过程，图5给出了四路合成的π/4 QPSK实现示意图。输入信号先经过串并转换，分成I、Q两路，I、Q两路经过差分编码得到xk和yk，xk和yk经过成形滤波后进行中频调制，得到四路π/4 QPSK。一三两路合并和二四两路合并后，送给DAC，得到模拟的π/4 QPSK信号。各个步骤中的仿真结果非常类似于1.1节给出的结果(这里不再赘述)，区别在于成形滤波器的设计，关于四路成形滤波器的设计将在第2节给出。

图5 四路合成π/4 QPSK示意图

2 多路合成的成形滤波器设计

2.1 成形滤波器基本原理

设计使用成形滤波器的原因主要是减少带外辐射的功率和减少码间串扰。成形滤波器有很多种如升余弦滤波器、高斯滤波器、TFM(Tame Frequency Modulation)[6-7]采用的滤波器等。GMSK和TFM中所采用的成形滤波器主要目的是为了带外辐射的功率，而码间串扰的抑制效果不明显。升余弦滤波器是利用奈奎斯特定理设计的，其主要目的是为了抑制码间串扰，同时能够达到较少带外辐射的功率的效果，因而被广泛采用。本文设计的π/4 QPSK采用的成形滤波器为升余弦滤波器的平方根形式，升余弦滤波器的频域表达式为

(5)

其中α为滚降因子。

(6)

2.2 基于查表的成形滤波器设计

根据图5所示，在对差分编码后的信号xk和yk进行成形滤波时，很难采用滤波器直接实现。假如DAC的采样频率为800 MHz，采用四路合成实现一个带宽为20 MHz的π/4 QPSK信号，则一个码元周期内采样10个点。如果对每一路采用采样倍数为10的成形滤波器进行滤波，最后四路合成得到的信号频谱如图6所示。显然出现了不期望的频谱分量，这些不期望的频谱分量会对其他频率上的信号产生影响。产生这些不期望的频谱分量的原因是本身信号是一个采样率为800 MHz的信号，每一码元应该采样40个点，在进行成形滤波时，应该采用采样倍数为40的成形滤波，而在操作过程中却使用了采样倍数为10的成形滤波器，所以造成了在其他频率分量上的频谱。如果直接利用800 MHz信号去进行采样，滤波器的采样倍数为40，这样会呈现出如图7的频谱，该频谱是我们所期望的。但是在FPGA实现时，800 MHz的采样速率很难实现，故利用采样倍数为40的滤波器是不可能直接实现的。

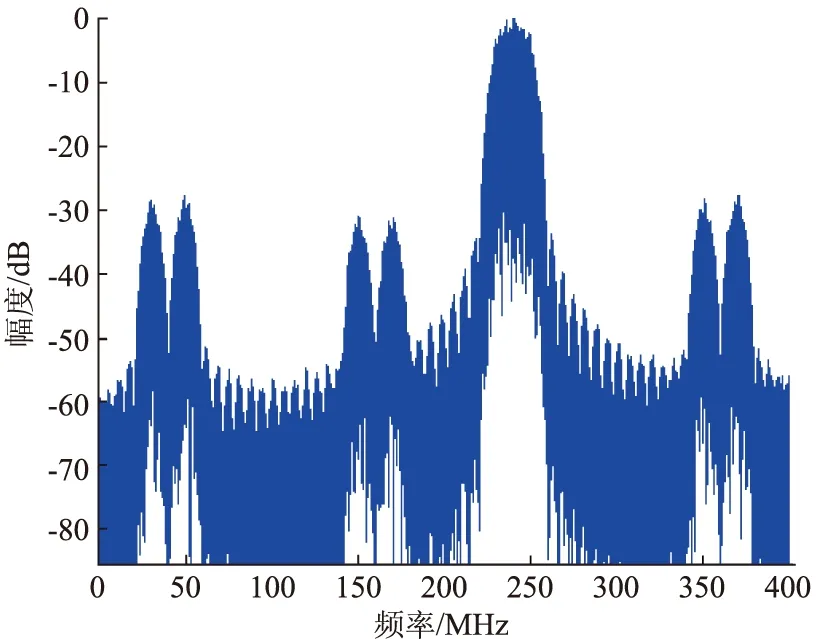
图6 利用采样倍数为10的成形滤波器四路合成信号的频谱

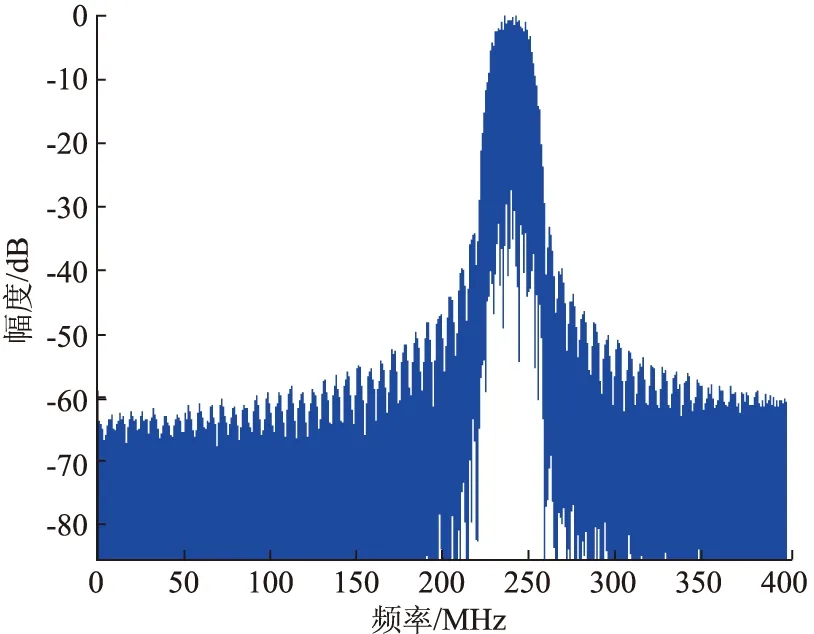
图7 利用采样倍数为40的成形滤波器单路路合成信号的频谱

解决方法是通过查表实现，也即首先求得所有输入的信号的可能性，然后对所有可能的输入信号进行采样倍数为40的成形滤波，求得每一种可能输入信号的滤波结果，建立一张滤波结果表。在进行信号调制时，根据输入的信号，求得滤波结果地址，然后查表即可得的滤波结果。

为了建立一张成形滤波后的表，需要计算输入信号的所有可能性。理论上的输入信号的可能性为无穷多，实际处理时我们不可能穷举。这里需要考察输入的信号或(和本质上是一样的，下面只考虑)对滤波结果产生影响的个数。

根据第1节的原理，我们知道有5种取值。假设我们认为输入的的滤波结果受到其后的5个码元的影响即xk+1、xk+2、xk+3、xk+4、xk+5(这里我们称[xkxk+1xk+2xk+3xk+4xk+5]为对滤波结果有影响的码元个数为6个)，也就是求出[xkxk+1xk+2xk+3xk+4xk+5]所有可能性，然后对每一种可能性进行滤波，根据要求的采用点数求得滤波结果，存储在5^6*(采样点数)大小的表内。在实际进行查表操作时，要根据输入的信号求得滤波结果存储的地址，那么为了求得这样一个地址，需要对xk的每一个取值进行编码，而根据第一节可以知道xk只有五种取值，也就是说xk是一个五进制数，对其编码后的结果如表2所示。

表2 相位值与编码结果对应表

如果有影响的码元个数为6个，则可以根据下面的公式可以求得滤波结果：

addr=addrxk·3125+addrxk+1·625+addrxk+2·

125+addrxk+3·25+addrxk+4·5+addrxk+5

(7)

同理如果有影响的码元个数为5个，则根据下面的公式可以求得滤波结果

addr=addrxk·625+addrxk+1·125+addrxk+2·

25+addrxk+3·5+addrxk+4

(8)

需要注意的是利用公式(7)和公式(8)求得到滤波结果是的滤波结果。

根据这一思想，我们对20个码元数据进行直接用滤波器实现的π/4 QPSK信号和通过查表滤波实现π/4 QPSK信号对比的结果如图8所示。其中成形滤波器的设计参数为：滚降因子α=0.8，响应码元个数为1.5，采样倍数为10。

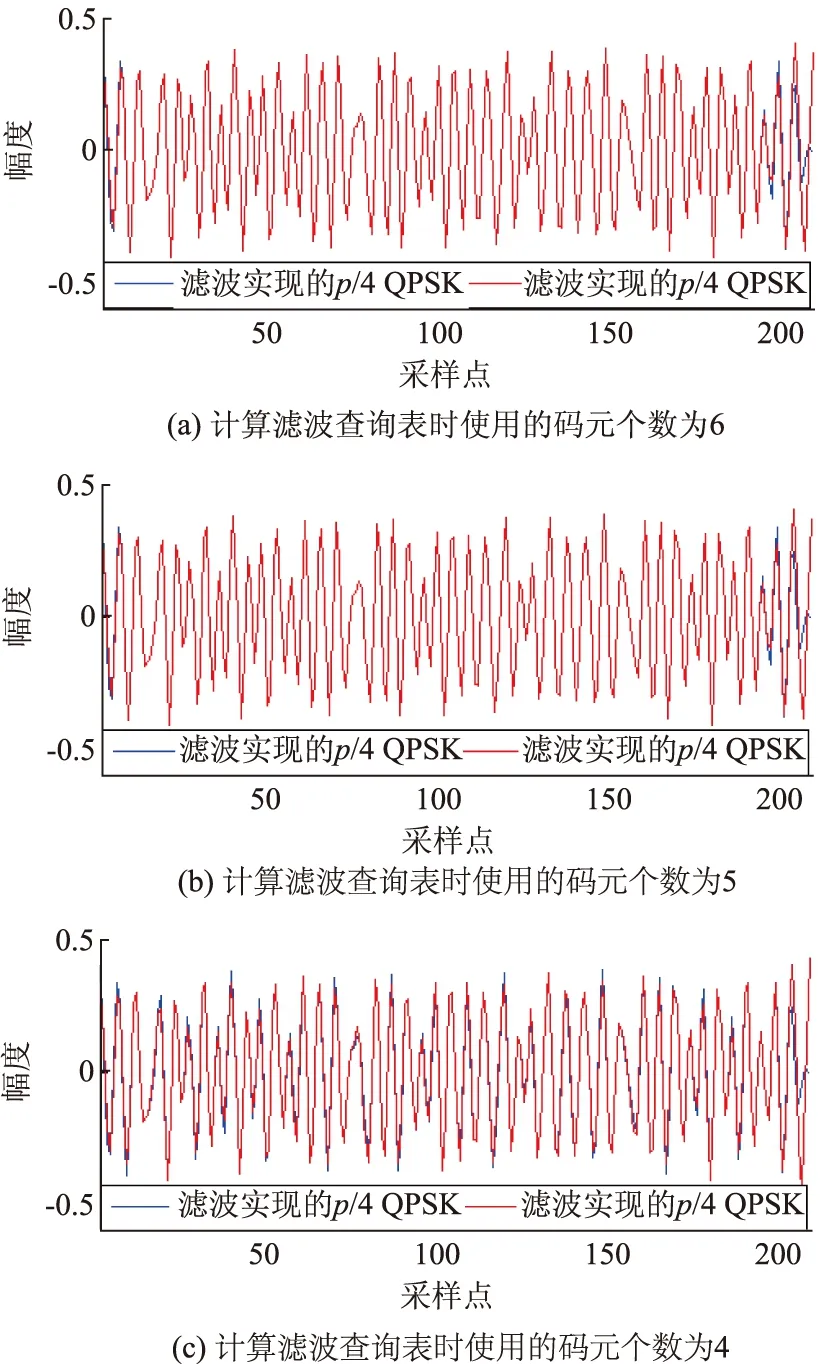
图8 滤波器实现的π/4 QPSK信号和查表实现的π/4 QPSK信号对比结果

图8(a)和图8(b)中开头和结尾契合度不好的原因是因为对于查表而言，需要通过输入的多个码元来求得滤波结果地址，然后通过查表得到滤波结果，在求第一或者最后几个码元的滤波结果时，根据公式(8)求得的结果是xk+2的滤波结果，如果要求得x0的结果，则根据公式(8)可以知道

addr=addrx-2·625+addrx-1·125+

addrx0·25+addrx1·5+addrx2

(9)

由于x0是第一个码元，x-1和x-2是不存在的，在实际的操作中认为addrx-2和addrx-1为0，所以导致开始的第一个和第二个码元的查表滤波的结果与直接用滤波器得到的结果不一致。

同理，一共有N个码元时，若要求xN的结果，则应根据公式(8)，可以得到

addr=addrxN-2·625+addrxN-1·125+addrxN·

25+addrxN+1·5+addrxN+2

(10)

由于xN已经是最后一个码元，xN+1和xN+1是不存在的，在实际的操作中认为addrxN+1和addrxN+2为0，所以导致最后几个码元的滤波结果不一致。

图8-(c)整体契合度不如图8-(a)和图8-(b)的效果好，这样会带来的效果是旁瓣比较高，如图9所示。而图8-(b)中通过查表实现的π/4 QPSK信号的频谱结果如图10所示，显然效果与图7的频谱结果基本一致。

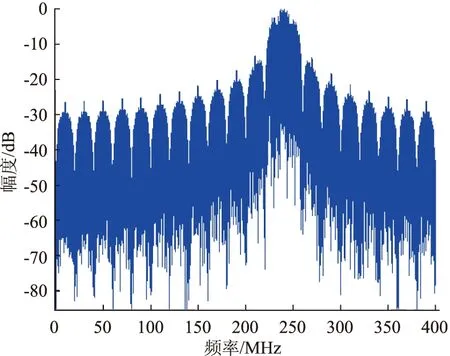
图9 图8-(c)的查表实现的π/4 QPSK信号的频谱

图10 图8-(b)的查表实现的π/4 QPSK信号的频谱

图11仿真了图8-(a)和图8-(b)中基于查表实现的π/4 QPSK二者之差的结果，这说明采用[xkxk+1xk+2xk+3xk+4]已经完全足够，没有必要再增加相互之间影响的码元个数。

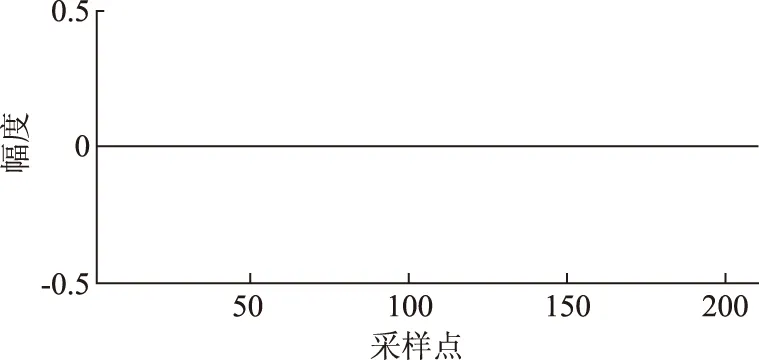
图11 图8-(a)和图8-(b)中基于查表实现的π/4 QPSK二者之差.

图12 响应码元个数为2，滤波查询表计算的码元个数为5的对比结果

图13 响应码元个数为2.5，滤波查询表计算的码元个数为6的对比结果

图14 响应码元个数为3，滤波查询表计算的码元个数为7的对比结果

3 解 调

解调方式一般有相干解调和非相干解调，而相干解调需要严格的载波同步。本文在进行解调时采用的是非相干解调中的中频差分解调方式(如图15)，这种解调方式可以直接求得解调结果，不需要再次进行差分解码。

图15 π/4 QPSK信号的中频差分解调示意图

基本的解调原理如下：

同样不考虑噪声，接收信号为

r(t)=A·cos(2·π·fc·t+φk+θ)

(11)

其中k·T≤t≤(k+1)·T,θ为固定的初始相位。

延迟T的信号为

r1(t)=r(t-T)=A·cos(2·π·fc·(t-T)+φk-1+θ)

(12)

由于fc·T一般为偶数，故

r1(t)=A·cos(2·π·fc·t+φk-1+θ)

(13)

希尔伯特变换后的信号为

r2(t)=A·sin(2·π·fc·t+φk+θ)

(14)

I通道乘法器的输出为

rI(t)=r1(t)·r(t) =

A2·cos(2·π·fc·t+φk+θ)·

cos(2·π·fc·t+φk-1+θ) =

cos(φk-φk-1)]

(15)

低通滤波后

(16)

Q通道乘法器的输出为

rQ(t)=r1(t)·r2(t) =

A2·sin(2·π·fc·t+φk+θ)·

cos(2·π·fc·t+φk-1+θ) =

sin(φk-φk-1)]

(17)

低通滤波后

(18)

对式(16)和式(18)进行抽样判决，即可得到 和 的值，再进行并串转换，得到码元信息。

非相干解调的理论误码率为

(19)

调制时采用了平方根升余弦滤波器，因此在图15 的低通滤波器应该采用平方根升余弦滤波器以使得信噪比最大化。调制时为了达到DAC的采样频率采用四路合成，解调时只需要一路进行解调即可。这里的平方根升余弦滤波器可以直接采用滤波器实现，采用的参数与调制时采用的参数一致，只是在采样倍数只使用一路的采样倍数即可，得到的误码率曲线为图16。仿真结果与理论结果一致。

图16 误码率仿真结果

4 结 语

本文详细设计分析了π/4 QPSK在调制时多路合成的原理。分析了基于查表的平方根升余弦滤波器和直接采用滤波器实现的平方根升余弦滤波器。并给出了设计基于查表的平方根升余弦滤波器的基本思想。分析了π/4 QPSK中频差分解调原理，对比了理论误码率曲线和仿真结果。

[1] 杨学志. 通信之道：从微积分到5G[M]. 北京：电子工业出版社， 2016.

[2] John G.Proakis著，张力军，张宗橙，郑宝玉等译. 数字通信[M]. 北京：电子工业出版社. 2003.

[3] 樊昌信，张莆翊，徐炳祥等. 通信原理(第五版)[M]. 北京：国防工业出版社，2001.

[4] Fuqin Xiong. Digital Modulation Techniques[M]. Artech House,INC, 2006.

[5] 杜勇. 数字调制解调技术的MATLAB与FPGA实现[M]. 北京：电子工业出版社，2014.

[6] De Jager F., and C. B. Dekker. Tamed Frequency Modulation, a Novel Method to Achieve Spectrum Economy in Digital Transmission [J]. IEEE Trans. on Comm., vol. 26, no. 5, May 1978, pp.534-542.

[7] 杜勇，路建功，李元洲. 数字滤波器的MATLAB与FPGA实现. 北京：电子工业出版社，2012.

刘志鹏(1987—)，山东人，工程师，主要研究方向为信道编解码、调制解调等；

E-mail：zhipengliu@live.cn

孙延坤(1988—)，山东人，主要研究方向为调制解调软硬件实现；

刘轶铭(1988—)，北京人，工程师，主要研究方向为高动态无线自组织网；

王兆伟(1982—)，天津人，高级工程师，主要研究方向为通信信号处理。

Design and Realization of Multi-channels π/4 QPSK

LIU Zhi-peng, SUN Yan-kun, LIU Yi-ming, WANG Zhao-wei

(China Academy of Electronics and Information Technology, Beijing 100041)

The modulation and demodulation of π/4 QPSK is studied. To achieve sampling rate of DAC, π/4 QPSK is realized by multi-channels. The design method of a square-root raised cosine filter based on query table is given. The spectrum of π/4 QPSK is realized by the square-root raised cosine filter, which is in comparison with the spectrum based on query table. The conclusion is that the needless spectrum is generated when the π/4 QPSK is realized by the square-root raised cosine filter based on filter. Multi-channels π/4 QPSK could be realized by the square-root raised cosine filter within query table. IF band differential detection method is analyzed, and the bit error rate is simulated. Simulation result is same as the theoretic result.

π/4 QPSK; raised cosine filter; multi-channels

10.3969/j.issn.1673-5692.2016.06.015

2016-07-01

2016-09-13

国家自然科学基金青年科学基金项目(61501415)

：A

1673-5692(2016)06-642-07