“锐角三角函数”中考新题型

□刘顿

“锐角三角函数”中考新题型

□刘顿

提到“锐角三角函数”，你就会想到中考，想到中考就自然会去看看又有哪些创新型试题，为方便你的寻求，现归纳几类，供参考！

一、渗透型

例1（2016·临沂）当α、β为任意角时，sin（α＋β）与sin（α－β）的值可以用下面的公式求得：sin（α＋β）＝sinα·cosβ+cosα·sinβ；sin（α－β）＝sinα·cosβ－cosα·sinβ.例如sin90°＝sin（60°＋30°）＝sin60°· cos30°＋cos60°·sin30°＝类似的，可以求得sin15°的值是.

分析：把15°化为60°－45°，则可利用sin（α－β）＝sinα·cosβcosα·sinβ和特殊角的三角函数值计算出sin15°的值.

解：sin15°＝sin（60°－45°）

＝sin60°·cos45°－cos60°·sin45°

点评：求解时要熟记特殊角的三角函数值，一是按值的变化规律去记，正弦逐渐增大，余弦逐渐减小，正切逐渐增大；二是按特殊直角三角形中各边特殊值规律去记.

二、阅读型

例2（2016·咸宁）阅读理解：我们知道，四边形具有不稳定性，容易变形，如图1，一个矩形发生变形后成为一个平行四边形，设这个平行四边形相邻两个内角中较小的一个内角为α，我们把的值叫做这个平行四边形的变形度.

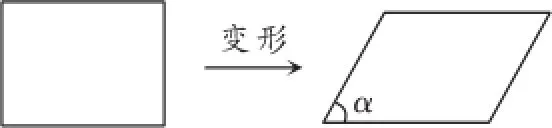
图1

（1）若矩形发生变形后的平行四边形有一个内角是120度，则这个平行四边形的变形度是.

（2）猜想证明：设矩形的面积为S1，其变形后的平行四边形面积为S2，试猜想S1、S2、之间的数量关系，并说明理由.

拓展探究：（3）如图2，在矩形ABCD中，E是AD边上的一点，且AB2＝AE·AD，这个矩形发生变形后为平行四边形A1B1C1D1，E1为E的对应点，连接B1E1，B1D1，若矩形ABCD的面积为，平行四边形A1B1C1D1的面积为试求∠A1E1B1＋∠A1D1B1的度数.

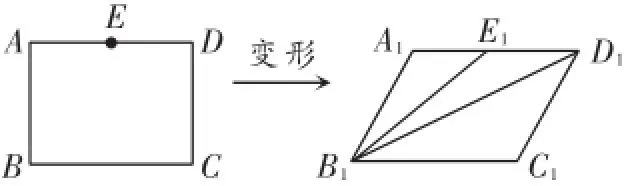
图2

分析：（1）根据平行四边形的性质得到α＝60°，根据三角函数的定义即可得到结论.

（2）若设如图1中矩形的长和宽分别为a、b，变形后的平行四边形的高为h，根据平行四边形和矩形的面积公式即可得到结论.

（3）由已知条件得到△B1A1E1∽△D1A1B1，由相似三角形的性质得到∠A1B1E1＝∠A1D1B1，根据平行线的性质得到∠A1E1B1＝∠C1B1E1，求得∠A1E1B1＋∠A1D1B1＝∠C1B1E1＋∠A1B1E1＝∠A1B1C1，证得∠A1B1C1＝30°，于是得到结论.

解：（1）∵平行四边形有一个内角是120度，∴α＝60°，

理由：如图1，设矩形的长和宽分别为a、b，变形后的平行四边形的高为h，

∴S1＝ab，S2＝ah

（3）∵AB2＝AE·AD，

而A1B1＝AB，A1E1＝AE，

A1D1＝AD，

∴A1B12＝A1E1·A1D1，

∵∠B1A1E1＝∠D1A1B1，

∴△B1A1E1∽△D1A1B1，

∴∠A1B1E1＝∠A1D1B1，

∵A1D1∥B1C1，

∴∠A1E1B1＝∠C1B1E1，

∴∠A1E1B1+∠A1D1B1

＝∠C1B1E1+∠A1B1E1＝∠A1B1C1.由（2）中的结论

∴sin∠A1B1C1

∴∠A1B1C1＝30°，

因此∠A1E1B1＋∠A1D1B1＝30°.

点评：本题通过阅读探究，考查了平行四边形的性质、矩形的性质、三角函数的定义，相似三角形的判定和性质，正确理解题意是解题的关键.

三、应用型

例3（2016·扬州）如图3，△ABC和△DEF中，AB＝AC，DE＝DF，∠A＝∠D.

图3

（2）由（1）中的结论可知，等腰三角形ABC中，当顶角∠A的大小确定时，它的对边（即底边BC）与邻边（即腰AB或AC）的比值也就确定，我们把这个比值记作T（A），即T（A）＝

①理解巩固：T（90°）＝，T（120°）＝，若α是等腰三角形的顶角，则T（α）的取值范围是；

②学以致用：如图4，圆锥的母线长为9，底面直径PQ＝8，一只蚂蚁从点P沿着圆锥的侧面爬行到点Q，求蚂蚁爬行的最短路径长（精确到0.1）.

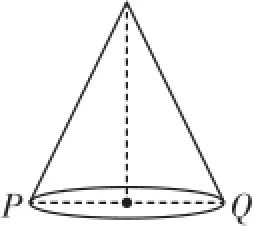
图4

（参考数据：T（160°）≈1.97，T（80°）≈1.29，T（40°）≈0.68）

分析：（1）证明△ABC∽△DEF，根据相似三角形的性质解答即可.

（2）①根据等腰直角三角形的性质和等腰三角形的性质进行计算即可；②根据圆锥的侧面展开图的知识和扇形的弧长公式计算，得到扇形的圆心角，根据T（A）的定义解答即可.

解：（1）∵AB＝AC，DE＝DF，

又∵∠A＝∠D，

∴△ABC∽△DEF，

图5

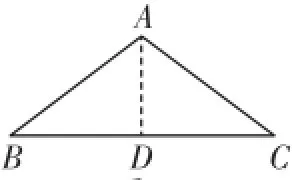
图6

如图6，∠A＝120°，AB＝AC，

作AD⊥BC于D，则∠B＝30°，

∵AB－AC＜BC＜AB＋AC，

∴0＜T（α）＜2.

②圆锥的侧面展开图如图7所示.

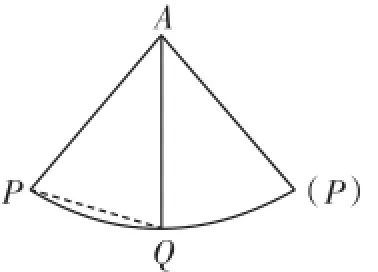
图7

∵圆锥的底面直径PQ＝8，

∴圆锥的底面周长为8π，即侧面展开图扇形的弧长为8π.

设扇形的圆心角为n°，

∵T（80°）≈1.29，

∴蚂蚁爬行的最短路径长为PQ＝1.29×9≈11.6.

点评：本题通过模仿锐角三角函数的定义，考查的是相似三角形的判定和性质、等腰三角形的性质以及T（A）的定义，正确理解T（A）的定义、掌握相似三角形的判定定理和性质定理是解题的关键.