复杂决策规则下MIRT的分类准确性和分类一致性*

汪文义 宋丽红 丁树良

(1江西师范大学计算机信息工程学院; 2江西师范大学初等教育学院, 南昌 330022)

1 引言

标准参照测验(CRT)关注学生具体知识或技能的掌握情况及达到的水平。CRT有助于发挥考试的诊断功能和促进学生发展, 从而对教育评价产生了深刻影响(戴海琦, 2010)。CRT的广泛应用或需求,很好地体现了其在教育评价中的重要性：教育部基础教育质量监测(NAEQ)中心开发的监测工具采用了CRT; 美国的“力争上游”教改计划中强调采用新型标准和评价, 促使学生在大学或工作岗位上取得成功, 在全球范围内具备更好的人才竞争力; 美国前教育部长阿恩·邓肯(Arne Duncan)曾表示“一旦建立和采用新标准, 就需要创建新测试, 测量学生是否满足这些标准” (Duncan, 2009)。CRT已经广泛应用于水平和资格考试等, 如国际学生评估项目(PISA)、国际阅读素养进步研究项目(PIRLS)、国际数学和科学成就趋势研究(TIMSS)、美国教育进步评价(NAEP)、美国研究生入学考试(GRE)、美国大学水平考试(CLEP)和NAEQ等(甘良梅, 余嘉元,2006; 辛涛, 李勉, 任晓琼, 2015)。

CRT一般将被试分为“掌握、未掌握”或“初级、中级、高级”等表现水平, 测量结果直接决定学习进程、被试选拔和教学质量评价等。而测量往往存在测量误差, 如何根据标准和综合各种测验分数对被试表现水平给出可靠而有效地评价, 以及如何量化评价分类结果的一致性和准确性, 成为研究者关注的重点(Douglas & Mislevy, 2010; 陈平, 李珍, 辛涛,高慧健, 2011)。

分类一致性是指两次平行测验中被试观察分类相同的概率, 主要反映测验信度; 分类准确性是指被试观察与真实分类相同的概率, 主要反映测验效度(Lee, Brennan, & Wan, 2009; 陈平等, 2011)。分类一致性和准确性指标的发展趋势为：从平行测验过渡到单个测验指标估计; 从经典测验理论(CTT)过渡到项目反应理论(IRT)下指标估计。本文关注IRT下单个测验指标估计, 这是该领域的研究热点之一(Guo, 2006; Lathrop & Cheng, 2013; Lee, 2010;Rudner, 2005; Wyse & Hao, 2012)。指标主要分为两类：一类是以Lee方法为代表的基于观察分数(测验总分)的决策指标; 另一类是以Rudner方法为代表的基于能力分数的决策指标(Lathrop & Cheng,2013; Rudner, 2005)。Guo方法作为Rudner方法的改良, 不像Rudner方法需要借助正态性假设(Guo,2006; Wyse & Hao, 2012), 因此本研究中暂不考虑Rudner方法。

这些研究仅从模拟或实证角度比较Lee和Guo指标表现, 本研究尝试从理论上寻求两类指标之间的内在关系。相关研究主要集中于单维IRT (UIRT)下指标估计, 而随着测量学研究的深入, 众多研究表明, 许多教育或心理测验, 如NAEP, PISA, TIMSS,NAEQ和西方五因素人格问卷(如NEO-PI-R), 都是多维测验(Debeer, Buchholz, Hartig, & Janssen, 2014;Makransky, Mortensen, & Glas, 2013; Rijmen, Jeon,von Davier, & Rabe-Hesketh, 2014; Yao & Boughton,2007; Zhang, 2012)。用于多维测验分析的多维IRT(MIRT)涌现了许多研究成果, 涉及模型、估计、等值、自适应测验和应用等方面(Cai, 2010; Reckase,2009; Wang, 2015; 刘红云, 骆方, 王玥, 张玉,2012; 杜文久, 肖涵敏, 2012; 康春花, 辛涛, 2010;毛秀珍, 辛涛, 2015; 涂冬波, 蔡艳, 戴海琦, 丁树良,2011; 许志勇, 丁树良, 钟君, 2013; 詹沛达, 王文中,王立君, 李晓敏, 2014)。

伴随着MIRT的发展, 近年来有研究将Lee方法推广用于估计多维测验的分类一致性和准确性,如Grima和Yao (2011)、Yao (2016)将Lee方法从UIRT推广到MIRT, 并指出使用UIRT分析多维数据会导致指标估计有偏; LaFond (2014)将Lee方法应用于双因子模型和题组模型。这两项研究均是基于Lee方法计算观察分数的分类一致性和准确性。而最近有研究表明, 在两或三参数逻辑斯蒂克模型和等级反应模型下, 基于能力分数的决策指标要优于基于观察分数的决策指标(Lathrop & Cheng,2013)。因此, 如何计算各内容、技能或能力分数上的分类一致性和准确性, 能否将基于能力分数的Guo方法推广到MIRT, UIRT下得出的结论在MIRT下是否仍成立, Guo与Lee方法在什么条件下等价,Guo或Lee方法是否具有独特的优势？这些是本文要探讨的主要问题。

对学生有重要影响(如影响受教育机会)的决策,教育与心理测量标准要求不能仅基于单个测验分数(Henderson-Montero, Julian, & Yen, 2003), 而要求使用多重测量结果做决策, 以提高测量信度、效度、公平性等(Chester, 2003; McBee, Peters, &Waterman, 2014)。在“中小学教育修正法”和“不让一个孩子掉队”法案推动下, 一般采用合成分数合成多重测量结果。合成方法常采用联合、补偿、联合−补偿混合和验证规则, 并应用于英语水平考试、通识教育发展考试和学业水平评价等(Abedi, 2004;Carroll & Bailey, 2015; Chester, 2003; Henderson-Montero et al., 2003)。以上关于决策规则的研究基本是集中于CTT。虽然MIRT非常适合分析多重测量结果, 如能反馈学生各方面内容、技能和能力的诊断信息(Chang, 2012; 康春花, 辛涛, 2010), 但是至今尚没有研究在MIRT框架下比较各种决策规则下的分类一致性和准确性。

基于以上文献回顾和分析, 提出如下实验假设：基于能力分数的Guo指标比基于观察分数的Lee指标更为灵活, 可方便计算各能力维度、联合和补偿等复杂规则下指标; 在计算多重积分方面具有独特优势的蒙特卡罗方法, 可较好地估计Guo和Lee指标。

2 多维等级反应模型和Lee方法

2.1 多维等级反应模型

给定观察数据y、项目参数α和β, 可基于极大似然法或其他方法(Wang, 2015)估计被试能力。能力为θ的似然函数为：

其中示性函数定义如下：

2.2 多维模型下Lee方法

2.2.1 基于Lee方法的分类一致性指标

该式表示总分为

x

的各个得分向量y的联合概率之和。根据

X

的条件分布和划界分数, 可计算能力为θ的被试位于或被分到第

h

类的概率：

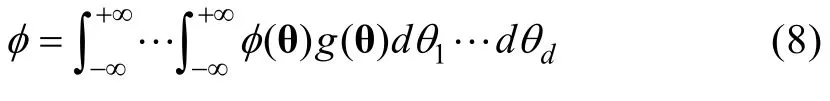
2.2.2 基于Lee方法的分类准确性指标

先计算能力的期望总分或真分数：

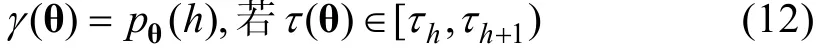
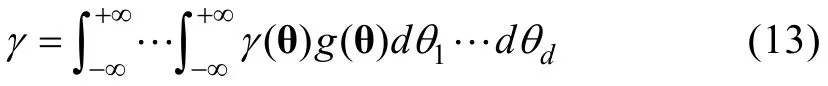
3 决策规则和新指标

3.1 决策规则

决策规则直接影响测验分类结果的信度和效度, 决策规则可分为联合、补偿及混合型等(Douglas& Mislevy, 2010)。如研究生入学考试要求考生在单科分数和总分均达到分数线, 这属于一种混合型规则。下面介绍三种多维潜在能力下的决策规则, 决策区域示意图见图1。

(1)基于各个能力分数的决策规则, 第

k

维能力上决策区域为：

(2)基于合成能力分数的决策规则, 决策区域为：

(3)基于各个能力和合成分数的决策规则, 决策区域为：

图1 三种决策规则对应的决策区域示意图(H=3, d=2)

3.2 基于Guo方法的分类一致性和准确性指标

根据Guo方法思想, 给定被试观察数据y、项目参数α和β, 可基于似然函数计算被试

i

分到第

h

类的期望概率为：

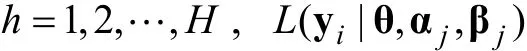
3.3 Guo方法和Lee方法下分类准确性指标的关系

4 模拟研究

4.1 研究目的

通过模拟研究探讨基于Guo方法估计的分类一致性和准确性是否可以准确地评价测验的模拟分类一致性和准确性。模拟分类一致性, 又称为重测一致性, 是通过模拟同一批被试在同一份测验上的独立作答两次, 然后计算两次测验上估计能力所在相同类的比率; 模拟分类准确性, 是指所有被试中模拟能力与估计能力属于同一类的比率。

4.2 研究设计

借鉴多维模型下模拟研究的实验设计(Wang,2015; Yao & Boughton, 2007), 为了评价测验长度、维度、相关和样本量的影响。采用四因素完全随机设计, 由于单维测验不能考虑能力间相关, 共28种实验条件。表1给出了固定样本量(1000和3000)水平下其他因素的条件组合。

表1 固定样本量水平下三个因素的实验条件

4.3 数据模拟

模拟研究中使用了R软件和Matlab R2015a软件, 其中MGRM的参数估计算法采用的是MH-RM算法(Cai, 2010)。因为有研究显示个体方法与分布方法结果类似(Lee, 2010), 因此本文中Lee方法指标均是基于个体方法计算, 即公式(8)和(13)采用样本中个体指标的平均, 即使用估计能力代替能力,并对所有被试指标求均值代替加权积分。因为随着测验项目数和等级数较多, 可能的项目反应模式数量非常大, 公式(6)采用蒙特卡罗方法模拟作答反应进行近似计算。采用马尔柯夫蒙特卡罗方法之Metropolis-Hastings构造独立链抽样并近似计算公式(17)的多重积分。

4.4 决策规则

将被试分为三类, 采用三种决策规则：(1)基于测验原始总分的决策规则, 划界分数设置为满分的50%和80%。当测验长度为15且所有项目的最高等级分为2时, 测验满分为30, 划界分数为15和24分; (2)基于各维度能力分数的决策规则, 各划界分数采用各能力维度下子测验满分的50%和80%。如四维模型下测验长度为30的测验, 每个能力维度上有10个项目(含测量两个维度的项目), 划界分数为10和16分; (3)基于合成能力分数的决策规则。公式(15)和(16)中能力权重设为维度的倒数, 而划界分数设为0和0.75。在前两种决策规则下, 可计算Lee和Guo方法指标。而在第三种决策规则下,由于不能建立能力子空间与总分子区间的一一对应关系, 只计算Guo方法指标。

表2 两维模型下的项目参数(Cai, 2010)

5 实验结果

5.1 总分决策规则下的指标误差评价

在总分决策规则下, 本部分主要给出指标误差的结果。指标误差来源主要有项目参数估计误差和蒙特卡罗方法近似计算误差。这是因为：在真实测验情景下, 并没有真实项目参数, 而只能基于参数估计软件估计项目参数, 再进行指标计算, 这个过程当中就存在项目参数的估计误差; 已知真实或估计的项目参数, 在指标计算过程中, 为避免维数灾难问题或样本空间特别大问题, 需要采用蒙特卡罗方法计算多重积分或获得估计能力条件下总分的经验分布, 此时, 蒙特卡罗方法中样本的抽样数量将影响近似计算精度。下面主要考虑真实或估计项目参数和三种抽样数量(1000,3000,9000)对指标误差的影响。

使用偏差(

bias

)、绝对偏差(

abs

)和误差均方根(

RMSE

)来反映真值与估计值差异大小。给定模拟项目参数, 由极大似然法估计被试能力, 然后分别计算估计能力、观测总分与模拟能力所在类相同的比率, 分别得到Guo或Lee方法的模拟分类准确性(Lathrop & Cheng, 2013)：

由模拟或估计的项目参数使用极大似然法估计被试能力, 再使用公式(13)和(19)估计分类准确性。

表3给出了在真实或估计项目参数、三种抽样数量条件下两类分类准确性指标的误差。结果显示：(1)对于分类准确性指标精度, 真实项目参数下精度好于估计项目参数下精度; (2)基于Lee方法的分类准确性指标精度已经基本上不受抽样数量影响, 这是因为总分随机变量的样本空间可数而能力空间不可数; (3)基于Guo方法的分类准确性指标精度随着抽样数量增加而提高。当抽样数量从1000增加到3000时,

RMSE

减少0.0035或0.001, 而当抽样数量增加到9000时, 估计精度增幅非常小; (4)精度并不完全随抽样数量增加而提高, 可能由于取样随机性引起。基于以上结果, 下面只对估计项目参数和抽样数量为3000的结果进行分析。

5.2 总分决策规则下的指标估计

表4给出真实项目参数下分类准确性指标的模拟值、估计项目参数下的分类准确性指标估计值及其对应的Kappa (两维模型和四维模型结果类似,为节省篇幅, 故两维模型结果未列出)。结果显示：(1)两类方法估计的分类准确性指标返真性好, 均可以准确地估计模拟分类准确性; (2)单维、两维和四维模型下, 分类准确性随着测验长度增加而严格递增; (3)单维模型下, 分类准确性并没有随样本量增加而提高, 存在一定的差异, 可能主要由于得分矩阵的随机性引起。另外, 样本量1000已经基本达到了单维模型下准确估计项目参数的要求, 并且分类准确性指标对项目参数估计误差不是太敏感(见表3); (4)两维模型和四维模型下, 分类准确性多数随样本量增加而有所提高。直观上, 维数越大需要估计的项目参数数量更多, 对样本量有更高要求;(5)两类方法的分类准确性均随着能力间相关增加而严格递增, 并且四维模型与两维模型的结果类似;(6)单维模型和两维模型下, Guo方法下的模拟或估计的分类准确性指标均稍高于Lee方法相应指标(但是两者相当接近, 与理论结果相符), 两种方法得到的估计值对应的Kappa有类似的趋势。而在四维模型下, 结果有所不同, 仅在相关为0.8时, Guo方法下分类准确性指标估计值的Kappa较明显高于Lee方法的Kappa; (7)相同条件下, 两类指标值差异相当小。表5给出了分类一致性, 结果类似于分类准确性, 在此不详细说明。

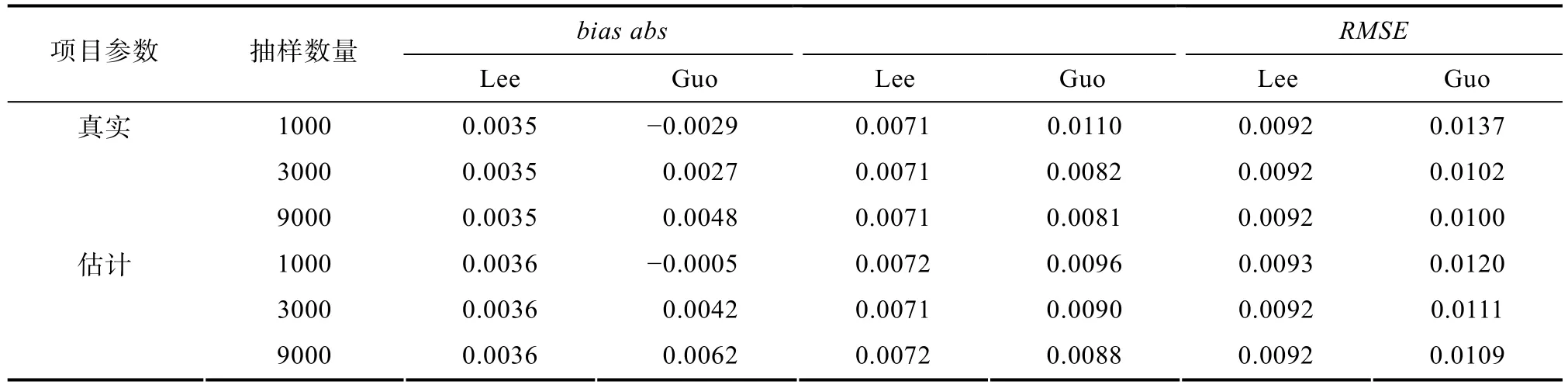
表3 模拟研究所有条件下两类分类准确性指标的三类误差指标的平均值

5.3 各能力维度决策规则下的指标估计

单维模型的维数为1, 能力维度决策规则与总分决策规则相同, 对应的指标估计相同, 结果不重复列出。由于设计的测验考虑了各能力维度上的项目数平衡, 各能力维度上的分类准确性十分接近,下面仅考虑第一个能力维度下指标的结果(其他结果未列出)。表6仅给出四维模型的真实项目参数下分类准确性指标的模拟值、估计项目参数下的分类准确性指标估计值及其对应的Kappa。

表6结果显示：(1)两类方法估计的分类准确性指标返真性好, Guo方法返真性稍好; (2)分类准确性随着测验长度增加而提高; (3)分类准确性并不随着样本量增加而提高, 可能由于相应子测验长度较短和得分阵中随机性导致; (4)分类准确性随着能力间相关增加而提高; (5)平均而言, Lee方法比Guo方法的分类准确性高; (6)相同条件下, 各能力维度决策规则比总分决策规则所得到的分类准确性要小, 这意味着, 在实际应用中报告各能力维度分数或内容领域分数时, 需要考虑其分类准确性是否达到指定的精度。该决策规则下的分类一致性指标与总分决策规则的分类一致性指标变化趋势相似, 只是值要小一些, 故结果省略。

表4 总分决策规则下分类准确性指标及估计值对应的Kappa (抽样数量为3000)

表5 总分决策规则下分类一致性指标及估计值对应的Kappa (抽样数量为3000)

表6 第一个能力维度决策规则下分类准确性指标及估计值对应的Kappa (抽样数量为3000)

5.4 合成能力决策规则下的指标估计

表7给出真实项目参数下分类一致性和准确性指标模拟值、估计项目参数下分类一致性和准确性指标估计值及其对应的Kappa (两维模型结果未列出)。结果显示：(1)两维模型和四维模型下, 推广的Guo方法能很好地估计合成能力规则下的分类一致性和准确性; (2)在单维模型下, 由于并没有其他能力维度参与合成, 其实就只有单个能力参与决策,但是基于能力量尺划界分数与总分决策规则的划界分数稍微有所差异。划界分数为满分50%基本上对应能力划界分数0, 而若总分服从正态分布, 可计算划界分数为满分80%对应的Z分数约为0.84,这与能力划界分数0.75稍有差异。划界分数对应的能力值也可以通过已知总分量尺上的划界分数, 由真分数计算公式迭代估计出对应的能力值(可参见戴海琦, 2010)。因此, 单维模型下的分类一致性和准确性指标与表4和表5中结果稍有差异。

表7 合成能力决策规则下分类一致性和准确性指标(抽样数量为3000)

6 讨论

6.1 新方法提出的背景和意义

CRT一般将被试分成少数几个表现水平, 从而可以较短测验长度获得较高的测量精度, 特别适合于大尺度教育评估等, 并且CRT有利于提高教学(戴海琦, 2010; Chang, 2012)。许多大尺度评估具有多维性, 为了更好地利用维度间的相关信息, MIRT成为分析这类测验的重要选择。信度和效度是评价测量工具质量的重要指标, 因此, 非常有必要开发分类信度和效度的评价指标。本研究正是在这样的背景之下, 探讨MIRT下CRT的分类一致性和准确性指标。

本研究在MIRT下推广分类一致性和准确性指标, 采用蒙特卡罗方法计算多重积分值, 实现复杂决策规则下指标计算, 并从数学上证明分类准确性两类估计量在总分决策规则和均匀先验下依概率收敛于同一真值。综合考虑测验长度、维度、相关、样本量和决策规则等对指标估计的影响, 研究表明,新指标及其估计方法表现不错, 可以在复杂决策规则下评价CRT分类信度和效度。如果划界分数直接定义在能力分数量尺之上, 相比Lee方法, Guo方法更适合于各个能力维度、联合和补偿等复杂规则下指标估计。

6.2 分类一致性和准确性的用处

分类一致性和准确性的估计方法的实际用处到底是什么、是否有替代方法、这些方法如何应用于真实测验情景和是否已经有应用的例子、以及在什么情景下需要使用新方法？这些问题十分重要,直接决定这类方法或新方法的推广性。为了清晰地阐明分类一致性和准确性或新方法的用处, 下面对这些问题分别进行说明。

第一, 新方法可用于估计单个测验的分类一致性和准确性, 无需进行重测、能力模拟和估计。一方面, 尽管测验的分类一致性可以通过重测得到,但是由于重测条件十分苛刻而要获得重测数据不太可能(Lee, 2010), 因此, 实际应用中较难直接通过重测获得分类一致性。另一方面, 由于在实际应用中真实能力并不知道, 估计分类准确性的模拟方法需要模拟并估计能力。即先根据估计能力和项目参数, 模拟作答数据再估计能力并比较两者分类相同的比率, 即模拟的分类准确性。由于估计能力并非被试的真实能力, 该模拟方法仍有不足之处。以上两方面的考虑, 正是众多研究者提出了其他方法估计单个测验的分类一致性和准确性的初衷。

第二, 条件标准误指标并不能直接反映测验的分类准确性。尽管CRT分类误差还可通过其他指标来衡量, 如条件标准误等指标(戴海琦, 2010)。由于条件标准误只能反映能力估计与“真值”之间的一种差异, 并不能直接以“百分比”的形式反映测验上所有被试的分类准确率。不过, 在UIRT和误差分布为正态分布条件下, 有研究者发现能力估计的标准误与分类准确性指标存在着一种较为复杂的非线性转换关系(Cheng, Liu, & Behrens, 2015)。理论上这种关系应该可以推广到MIRT, 但仍需要进行相关研究。

第三, 新方法或指标并不仅仅能用于模拟研究,更为重要是可以应用于实证研究。首先, 在真实测验情景下, 由于被试真实能力未知, 无法得到分类准确性真值, 本文开展的模拟研究只是为了验证新指标的表现。一般来讲, 模拟研究的逻辑是, 如果模拟条件下结果不好, 那么在错综复杂的真实情况下结果一般更加差, 即模拟研究至少可以起到淘汰作用。结合本文来说, 如果在相当理想的模拟条件下, 新指标不能很好地估计真实的分类一致性和准确性, 那么在更加复杂的实际情况中, 新指标就不可用。其次, 从文中叙述的方法和条件来看, 新方法或指标完全可用于真实测验情景。本文叙述的复杂决策规则下MIRT的分类一致性和准确性估计方法, 只要将相关算法嵌入到相应的MIRT参数估计程序中, 基于测验作答数据、参数估计结果和决策规则, 就可估计真实测验的分类一致性和准确性。相关研究显示, 有些分类一致性和准确性估计方法已应用于真实测验, 如在UIRT或其他模型下,Lathrop和Cheng (2014)在其文中的引言中提到(pp.318−319), 前人提出的分类一致性和准确性估计方法, 包括本文中用到的Lee方法, 已用于评价许多实际测验的分类结果质量, 并且已经开发可供用户使用的专门商业或免费软件。

第四, 新方法或指标可用于复杂决策规则下多维测验的领域分数报告质量评价。领域分数主要反映学生在一组代表某个内容和技能的试题(领域)上的表现, 这比量表分或测验总分更直接, 更能被大众理解和接受(辛涛, 谢敏, 2010)。基于IRT的领域分数更具有优势。根据题目与潜在维度之间的关系,多维模型或测验主要分为两类：“题目间多维”和“题目内多维”, 其中题目间多维测验的各个题目仅能测量多个潜在维度中一个; 而题目内多维测验允许每个题目考察多个潜在维度(Adams, Wilson, &Wang, 1997)。题目间多维测验的领域分数报告研究较多(Yao, 2016; Yao & Boughton, 2007), 而题目内多维测验仅有报告能力领域分数(Yao, 2010)。在复杂决策规则下, 新指标可用于评估这两类测验的分类准确率和一致性, 从而丰富分数报告内容。

6.3 研究不足和有待进一步探讨的问题

基于Guo方法的新指标可根据不同决策规则计算分类一致性和准确性, 不需要复杂的计算程序。Guo方法不像Rudner指标(Rudner, 2005; Wyse& Hao, 2012)需要借助正态性假设(Guo, 2006), 可适合于非正态性数据, 同时可避免分数分布正态性转换可能带来分类结果的不同(Douglas & Mislevy,2010)。但是本研究并没有模拟非正态分布能力, 以检验Guo指标对于非正态数据的稳健性。能力分布为非正态分布条件下, 指标表现如何？有待研究。

尽管Guo方法并不需要能力误差具有正态性假设, 但是需要利用IRT下的似然函数, 因此Guo方法的表现依赖于模型－资料拟合情况。如果模型－资料拟合不好, 对Guo方法的影响如何？是否有更好的替代方法？最近有研究基于非参数统计中假设更弱的密度估计方法用于估计总分的平滑分布, 并用于估计分类一致性和准确性(Lathrop &Cheng, 2014)。非参数方法, 能否用于多维情形下各种决策规则下的分类一致性和准确性估计, 仍有待考虑。

MIRT下, 如何基于Rudner方法(Rudner, 2005;Wyse & Hao, 2012)估计分类一致性和准确性？值得研究。Rudner指标需要借助能力估计的误差矩阵或信息矩阵来计算, 能力的信息矩阵的不同估计方法也将影响指标的结果。信息矩阵哪一种估计方法更有利于估计分类一致性和准确性, 仍值得研究。如果在测验长度较长时, 极大似然法估计的能力误差渐近服从多元正态分布。而多元正态分布随机向量落在任意区域的概率的计算相对容易, 或可为分类一致性和准确性的计算带来一定的方便。

本研究采用了内容平衡技术生成多维测验, 因此采用了相同权重得到合成分数, 并计算其分类一致性和准确性。若以合成能力分数信息量最大的方式求取权重(Yao, 2010), 这样合成能力分数的分类一致性和准确性如何值得探讨。基于各内容领域的观察分数的如何合成, 及其分类一致性和准确性评价也值得考虑。在特定应用领域, 使用哪种决策规则, 需要综合考虑决策目的、信度、效度、公平性和风险等因素。另外, 有待开展新指标在真实的CRT或计算机分类测验中的应用。

7 结论

本研究探讨了MGRM下的分类一致性和准确性指标, 并采用蒙特卡罗方法模拟样本进行指标估计。研究表明：

(1)基于Guo方法(Guo, 2006; Wyse & Hao,2012)提出的多维模型下的分类一致性和准确性指标, 可准确地评价多维CRT的分类信度和效度;

(2)相比Lee方法, Guo方法更加灵活, 适用于多种决策规则指标估计, 不仅可用于观察总分、各个内容或技能分数指标估计, 还适宜于合成分数等复杂决策规则下分类一致性和准确性指标估计;

(3)多维模型下基于能力分数的Guo方法比基于观察总分的Lee方法得到的分类一致性略高, 分类准确性在能力间相关较大时更高。因此, 如果IRT拟合测验数据, 更适合基于能力做决策。单维等级反应模型下的基于能力分数的决策更准确,Lathrop和Cheng (2013)在比较Lee方法和Rudner方法, 也有相同的发现。

(4)在总分决策规则和无信息先验分布下(即先验分布为均匀分布), 从数学上证明了两种方法下分类准确性指标估计量依概率收敛于同一真值。

Abedi, J. (2004). The No Child Left Behind Act and English language learners: Assessment and accountability issues.

Educational Researcher, 33

(1), 4–14.Adams, R. J., Wilson, M., & Wang, W. C. (1997). The multidimensional random coefficients multinomial logit model.

Applied Psychological Measurement, 21

(1), 1–23.Cai, L. (2010). High-dimensional exploratory item factor analysis by a Metropolis–Hastings Robbins–Monro algorithm.

Psychometrika, 75

(1), 33–57.Carroll, P. E., & Bailey, A. L. (2016). Do decision rules matter?A descriptive study of English language proficiency assessment classifications for English-language learners and native English speakers in fifth grade.

Language Testing, 33

(1), 23–52.Chang, H. H. (2012). Making computerized adaptive testing diagnostic tools for schools. In R. W. Lissitz & H. Jiao(Eds.),

Computers an d their impact on st ate as sessment:Recent history and predictions for the future

(pp. 195–226.).Charlotte, NC: Information Age.Chen, P., Li, Z., Xin, T., & Gao, H. J. (2011). A review of decision consistency indices of criteria-reference test.

Psychological Development and Education, 27

(2), 210–215.[陈平, 李珍, 辛涛, 高慧健. (2011). 标准参照测验决策一致性指标研究的总结与展望.

心理发展与教育, 27

(2),210–215.]Cheng, Y., Liu, C., & Behrens, J. (2015). Standard error of ability estimates and the classification accuracy and consistency of binary decisions.

Psychometrika, 8 0

(3),645–664.Chester, M. D. (2003). Multiple measures and high-stakes decisions: A framework for combining measures.

Educational Measurement: Issues and Practice, 22

(2), 32–41.Dai, H. Q. (2010).

Psychometrics

. Beijing, China: Higher Education Press.[戴海琦. (2010).

心理测量学

. 北京: 高等教育出版社.]Du, W. J., & Xiao, H. M. (2012). Multidimensional grade response model.

Acta Psychologica Sinica, 44

(10), 1402–1407.[杜文久, 肖涵敏. (2012). 多维项目反应理论等级反应模型.

心理学报, 44

(10), 1402–1407.]Debeer, D., Buchholz, J., Hartig, J., & Janssen, R. (2014).Student, school, and country differences in sustained test-taking effort in the 2009 PISA reading assessment.

Journal of Ed ucational and Be havioral Statistics, 39

(6),502–523.Douglas, K. M., & Mislevy, R. J. (2010). Estimating classification accuracy for complex decision rules based on multiple scores.

Journal o f E ducational an d B ehavioral Statistics, 35

(3), 280–306.

Duncan, A. (2009, June 14). Address by the secretary of education at the 2009 governors education symposium:States will lead the way towards reform. Washington, DC:U.S. Department of Education. Retrieved May 10, 2016,from http://www2.ed.gov/news/speeches/2009/06/06142009.pdf

Gan, L. M., & Yu, J. Y. (2006). The study of criterion referenced test's score system.

Psychological Exploration,26

(3), 79–83.[甘良梅, 余嘉元. (2006). 标准参照测验分数体系的探讨研究.

心理学探新, 26

(3), 79–83.]Grima, A., & Yao, L. H. (2011).

Classification consistency and accuracy fo r test of mix ed item ty pes: U nidimensional versus multidimensional IRT procedures

. Paper presented at the annual meeting of National Council on Measurement in Education, New Orleans, LA.Guo, F. M. (2006). Expected classification accuracy using the latent distribution.

Practical A ssessment, Res earch &Evaluation, 11

(6), 1–6.Henderson-Montero, D., Julian, M. W., & Yen, W. M. (2003).Multiple measures: alternative design and analysis models.

Educational Measurement: Is sues a nd Pr actice, 22

(2),7–12.Kang, C. H., & Xin, T. (2010). New development in test theory:Multidimensional item response theory.

Advances i n Psychological Science, 18

(3), 530–536[康春花, 辛涛. (2010). 测验理论的新发展: 多维项目反应理论.

心理科学进展, 18

(3), 530–536.]Kroehne, U., Goldhammer, F., & Partchev, I. (2014).Constrained multidimensional adaptive testing without intermixing items from different dimensions.

Psychological Test and Assessment Modeling, 56

(4), 348–367.LaFond, L. J. (2014).

Decision co nsistency and ac curacy indices for the bifactor and testlet response theory models

(Unpublished doctorial dissertation). University of Iowa.Lathrop, Q. N., & Cheng, Y. (2013). Two approaches to estimation of classification accuracy rate under item response theory.

Applied Ps ychological M easurement,37

(3), 226–241.Lathrop, Q. N., & Cheng, Y. (2014). A nonparametric approach to estimate classification accuracy and consistency.

Journal of Educational Measurement, 51

(3), 318–334.Lee, W. C. (2010). Classification consistency and accuracy for complex assessments using item response theory.

Journal of Educational Measurement, 47

(1), 1–17.Lee, W. C., Brennan, R. L., & Wan, L. (2009). Classification consistency and accuracy for complex assessments under the compound multinomial model.

Applied Psy chological Measurement, 33

(5), 374–390.Liu, H. Y., Luo, F., Wang, Y., & Zhang, Y. (2012). Item parameter estimation for multidimensional measurement:Comparisons of SEM and MIRT based methods.

Acta Psychologica Sinica, 44

(1), 121–132.[刘红云, 骆方, 王玥, 张玉. (2012). 多维测验项目参数的估计: 基于SEM与MIRT方法的比较.

心理学报, 44

(11),121–132.]Makransky, G., Mortensen, E. L., & Glas, C. A. W. (2013).Improving personality facet scores with multidimensional computer adaptive testing: An illustration with the Neo Pi-R.

Assessment, 20

(1), 3–13.Mao, X. Z., & Xin, T. (2015). Multidimensional computerized adaptive testing: Model, techniques and methods.

Advances in Psychological Science, 23

(5), 907–918.[毛秀珍, 辛涛. (2015). 多维计算机化自适应测验: 模型、技术和方法.

心理科学进展, 23

(5), 907–918.]McBee, M. T., Peters, S. J., & Waterman, C. (2014).Combining scores in multiple-criteria assessment systems:The impact of combination rule.

Gifted Ch ild Q uarterly,58

(1), 69–89.Reckase, M. D. (2009).

Multidimensional item response theory

.New York: Springer.Rijmen, F., Jeon, M., von Davier, M., & Rabe-Hesketh, S.(2014). A third-order item response theory model for modeling the effects of domains and subdomains in large-scale educational assessment surveys.

Journal o f Educational and Behavioral Statistics, 39

(4), 235–256.Rudner, L. M. (2005). Expected classification accuracy.

Practical Assessment, Research & Evaluation, 10

(13), 1–4.Tu, D. B., Cai, Y., Dai, H. Q., & Ding, S. L. (2011).Parameters estimation of MIRT model and its application in psychological tests.

Acta Ps ychologica Si nica, 43

(11),1329–1340.[涂冬波, 蔡艳, 戴海琦, 丁树良. (2011). 多维项目反应理论:参数估计及其在心理测验中的应用.

心理学报, 43

(11),1329–1340.]Wang, C. (2015). On latent trait estimation in multidimensional compensatory item response models.

Psychometrika, 80

(2),428–449.Wyse, A. E., & Hao, S. Q. (2012). An evaluation of item response theory classification accuracy and consistency indices.

Applied Psychological Measurement, 36

(7), 602–624.Xin, T., Li, M., & Ren, X. Q. (2015).

Reporting and using the results of national assessment of education quality

. Beijing,China: Beijing Normal University Publishing Group.[辛涛, 李勉, 任晓琼. (2015).

基础教育质量监测报告撰写与结果应用

. 北京: 北京师范大学出版集团.]Xin, T., & Xie, M. (2010). Group-level domain score and its estimation methods.

Psychological D evelopment and Education, 26

(4), 416–422.[辛涛, 谢敏. (2010). 群体水平领域分数及其估计方法.

心理发展与教育, 26

(4), 416–422.]Xu, Z. Y., Ding, S. L., & Zhong, J. (2013). The analysis and application of MIRT in mathematics paper in college entrance examination.

Psychological Ex ploration, 33

(5),438–443.[许志勇, 丁树良, 钟君. (2013). 高考数学试卷多维项目反应理论的分析及应用.

心理学探新, 33

(5), 438– 443.]Xu, W. N., Wang, P. X., Han, P., Yan, T. L., & Zhang, S. Y.(2011). Application of Kappa coefficient to accuracy assessments of drought forecasting model: A case study of guanzhong plain.

Journal of Natural Disasters, 20

(6), 81–86.[许文宁, 王鹏新, 韩萍, 严泰来, 张树誉. (2011). Kappa系数在干旱预测模型精度评价中的应用——以关中平原的干旱预测为例.

自然灾害学报, 20

(6), 81–86.]Yao, L. H. (2010). Reporting valid and reliable overall scores and domain scores.

Journal of Educational Measurement,47

(3), 339–360.Yao, L. H. (2012). Multidimensional CAT item selection methods for domain scores and composite scores: Theory and applications.

Psychometrika, 77

(3), 495–523.

Yao, L. H. (2016). The BMIRT toolkit. Retrieved August 8,2016, from http://www.bmirt.com/media/f5abb5352d553d5fffff807cffff d524.pdf

Yao, L. H., & Boughton, K. A. (2007). A multidimensional item response modeling approach for improving subscale proficiency estimation and classification.

Applied Psychological Measurement, 31

(2), 83–105.Zhan, P. D., Wang, W. C., Wang, L. J., & Li, X. M. (2014).The multidimensional testlet-effect Rasch model.

Acta Psychologica Sinica, 46

(8), 1208–1222.[詹沛达, 王文中, 王立君, 李晓敏. (2014). 多维题组效应Rasch模型.

心理学报, 46

(8), 1208–1222.]Zhang, J. M. (2012). Calibration of response data using MIRT models with simple and mixed structures.

Applied Psychological Measurement, 36

(5), 375–398.