一种磁悬浮离心式心脏泵刚度与阻尼特性分析

李　波，孙传余，文艺成，丁鸿昌

(山东科技大学机械电子工程学院，山东 青岛 266590)

Study on Stiffness and Damping of a Centrifugal Maglev Blood Pump

LI Bo，SUN Chuanyu，WEN Yicheng，DING Hongchang

(College of Mechanical and Electronic Engineering，Shandong University of Science and Technology，Qingdao 266590，China)



一种磁悬浮离心式心脏泵刚度与阻尼特性分析

李波，孙传余，文艺成，丁鸿昌

(山东科技大学机械电子工程学院，山东 青岛 266590)

Study on Stiffness and Damping of a Centrifugal Maglev Blood Pump

LI Bo，SUN Chuanyu，WEN Yicheng，DING Hongchang

(College of Mechanical and Electronic Engineering，Shandong University of Science and Technology，Qingdao 266590，China)

摘要：针对一种磁悬浮离心式心脏泵系统的动态特性，需要分析其刚度与阻尼。为此，分析了径向永磁轴承和开关磁阻电机的径向力学特性，得到磁悬浮转子径向运动方程和控制系统框图；并结合PD控制器，推导出系统径向刚度与阻尼数学表达式，最后通过实例仿真，得到径向刚度与阻尼特性曲线。研究表明，比例和滤波环节对系统动刚度、阻尼比和固有频率均有显著影响，且在低频段，微分系数与阻尼比近似成正比关系。上述研究为磁悬浮离心式心脏泵控制系统的设计和磁悬浮转子径向位移控制提供理论指导。

关键词：磁悬浮心脏泵；径向永磁轴承；开关磁阻电机；刚度；阻尼

0引言

近年来，随着心脏病发病患者人数不断增加，磁悬浮心脏泵作为部分或全部替代人体心脏的医学装置，显得越来越重要。

第1代人工心脏泵模拟心脏的收缩与舒张过程，通过容积周期性变化，实现血液驱动，该心脏泵结构复杂、体积大且使用寿命短；第2代人工心脏利用机械轴承支承转子叶轮，该心脏泵机械摩擦严重，易引发溶血、血拴等问题，制约人工心脏泵在人体内的长期使用；第3代人工心脏泵采用非接触磁悬浮技术，通过转子叶轮的无接触高速旋转，驱动血液流动。磁悬浮心脏泵因其结构简单、体积小、无摩擦损耗已成为磁悬浮领域的热点问题。系统稳定性是磁悬浮心脏泵的重要技术指标，直接影响着心脏泵的整体性能，而系统稳定性与控制系统的刚度和阻尼有着重要联系。因此，研究心脏泵的控制系统的刚度与阻尼特性具有重要意义。

1磁悬浮离心式心脏泵原理

磁悬浮离心式心脏泵结构如图1所示，转子叶轮与定子绕组构成双定子单转子双绕组开关磁阻电机，其中转子叶轮在导通磁路的同时，驱动液体流动。转子叶轮两端设有径向永磁轴承，提供径向和轴向永磁偏置。定子绕组包括主绕组和悬浮力绕组，前者提供转动扭矩，后者提供径向二自由度电磁力。在开关磁阻电机驱动下，液体由入口流入，出口流出。

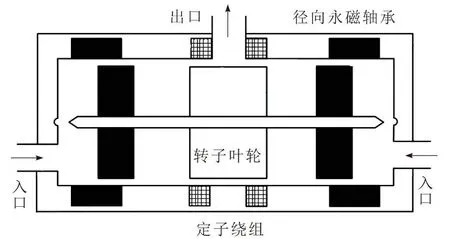
图1　磁悬浮心脏泵结构

2径向永磁轴承与开关磁阻电机力学特性

2.1　径向永磁轴承力学特性

心脏泵的径向永磁轴承由2部分组成，分别是左径向永磁轴承和右径向永磁轴承。如图2所示，忽略磁悬浮转子重力影响，分析径向永磁轴承在径向α方向、径向β方向和轴向z方向的永磁力与偏移量的关系，图中仅绘制左径向永磁轴承部分。

图2　径向永磁轴承力学分析

由于磁悬浮转子的位置偏移为微小量，认为在运动过程中径向永磁轴承的轴向刚度Kpz、径向刚度Kpr保持不变，即径向永磁轴承α向力、β向力和z向力仅与相应方向的偏移量Δα、Δβ、Δz相关。即有：

(1)

Fpα、Fpβ、Fpz分别为径向永磁轴承α向力、β向力和z向力；Δα、Δβ、Δz分别为α、β、z方向位置偏移量。

2.2　开关磁阻电机力学特性

磁悬浮心脏泵开关磁阻电机[4-5]为双定子单转子双绕组结构，其每一绕组均包括主绕组和悬浮力绕组。

已知单定子单转子双绕组磁阻电机数学模型为：

(2)

Feα和Feβ分别为α向和β向电磁力；im为主绕组控制电流；isa1和isa2分别为α和β方向悬浮力绕组控制电流；Kf(θ)为悬浮力系数，与旋转位置角θ相关。

则本磁悬浮心脏泵中双定子单转子双绕组开关磁阻电机数学模型为：

(3)

3刚度与阻尼特性分析

3.1　磁悬浮PID控制系统

磁悬浮转子径向位置，由径向永磁轴承和开关磁阻电机共同控制，联立式(1)和(3)，得磁悬浮转子α方向和β方向力学特性为：

(4)

Fα、Fβ为转子所受α、β方向合力。

根据式(4)建立磁悬浮转子径向二自由度运动学方程为：

(5)

根据径向二自由度运动方程，以α方向为例，绘制系统控制框图，如图3所示。

图3　转子α向控制框图

基于控制框图，磁悬浮转子α向偏移量Δα与干扰力Fdα的s域闭环传递函数为：

(6)

Gc(s)为α向PID控制器传递函数；Ks为α向位置偏移传感器增益；Ka为功率放大器增益。

同理，可绘制磁悬浮转子β向控制框图并得到闭环传递函数。

3.2　刚度与阻尼特性

根据磁悬浮心脏泵PID控制系统及闭环传递函数，可得磁悬浮心脏泵系统α向刚度Kα和阻尼dα为：

(7)

ω为磁悬浮转子振动频率；Re[Gc(s)]与Im[Gc(s)]分别为α向控制器传递函数的实数部分和虚数部分。

即磁悬浮心脏泵系统α向刚度Kα和阻尼dα与PID控制器传递函数Gc(s)相关。对于闭环控制系统，比例和微分环节必不可少，为了消除噪声等对微分环节的干扰，常在微分器中引入滤波环节。即对于含有滤波环节的PD控制器，有如下传递函数：

(8)

cp为比例系数；cd为微分系数；τd为滤波环节时间常数，为满足滤波环节滤波特性，需τd≥1/(2πf0)，其中f0为干扰信号频率。

将式(8)带入式(7)中，并将s域转换到频域(即s=jw)，得：

(9)

系统刚度Kα对系统稳定性有着直接影响。刚度太小，抗干扰能力差，稳定性不足；刚度太大，对冲击干扰反应剧烈，导致磁悬浮转子振动。对于永磁被动调节，外界干扰力较小时，至少要求Kα≥5 G/r0，其中G为转子重力，r0为径向气隙。

由式(9)知：磁悬浮转子α向刚度Kα和阻尼dα，均与PD控制器参数和磁悬浮转子振动频率相关，且Kα还与径向永磁轴承径向刚度Kpr相关；径向刚度Kpr增加了系统的正刚度，提高系统抗干扰能力，与永磁偏置混合磁轴承的永磁部分增加系统负刚度有较大不同。

为更好反映系统稳定性能，引入参数为：

(10)

m为磁悬浮心脏泵转子质量；Kdy为系统动刚度，反映力与位置偏移量的动态特性；ε为阻尼比，一般取0.5<ε<1，为使得系统稳定时间最短，常令ε=0.707；ωn为系统固有频率，为避免共振发生，常令ωn≥1.1ω0，其中ω0为心脏泵转子振动频率。

4仿真分析

磁悬浮心脏泵实验，系统基准参数选择：m=100 g，Cp=1.1，τd=0.1 ms，Cd=0.002，KsKaKi=70 000 N/m，Kpr=10 000 N/m。仿真曲线如图4、图5和图6所示，曲线参数未做具体说明时，均采用基准参数。

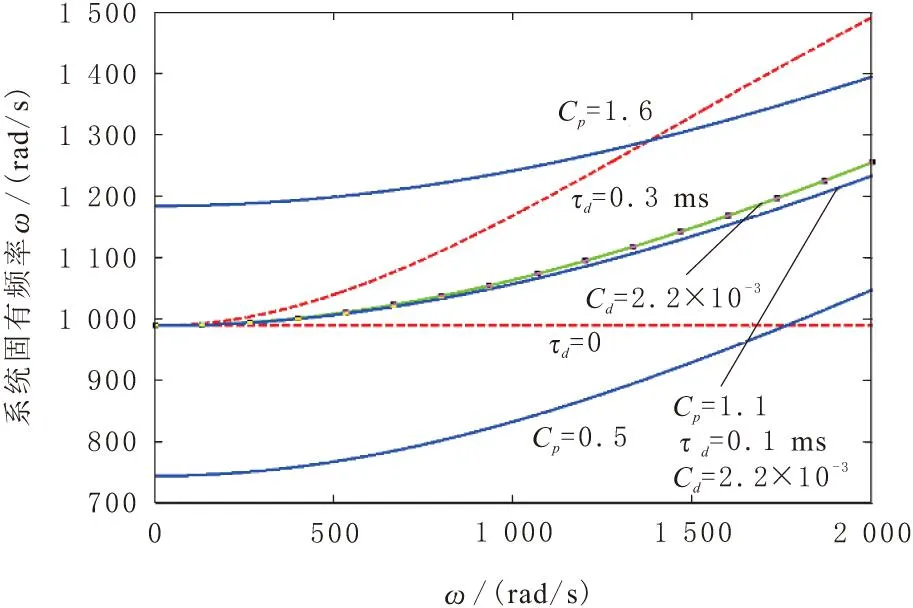
图4　系统固有频率特性曲线

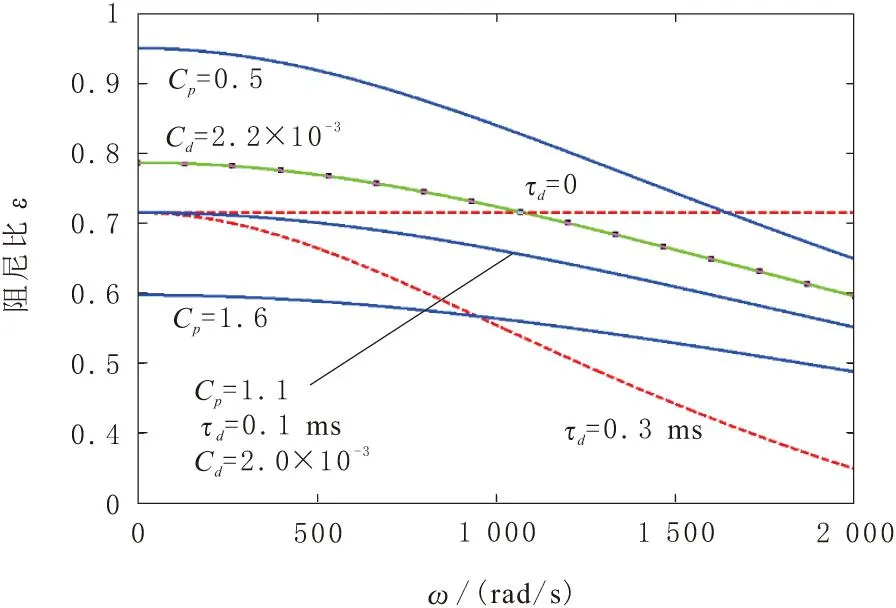
图5　系统阻尼比特性曲线

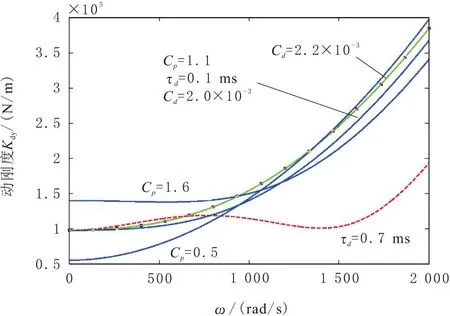
图6　系统动刚度特性曲线

由仿真曲线知，在低频段，随比例系数的增大，动刚度和系统固有频率明显增加，阻尼比明显减小，而刚度值的增加，使得系统功耗增加。当比例系数过大和过小时，动刚度稳定性不足。

不同微分系数下，动刚度和系统固有频率在ω=0时，保持恒定。在低频段，随微分系数的增大，阻尼比近似成正比例增加，动刚度和系统固有频率无显著变化。基于上述特性，适当调整微分系数，可在动刚度和系统固有频率基本不变前提下，调节阻尼比，缩短系统稳定时间，提高系统稳定性。

不同时间常数下，动刚度、阻尼比和系统固有频率在ω=0时，保持恒定，且当时间常数为0时，阻尼比和系统固有频率不随频率值变化。在低频段，随着频率的增加，时间常数越大系统固有频率越大，阻尼比越小。当时间常数过大时，动刚度在系统固有频率处减小，系统稳定性降低，且时间常数的设定应满足滤波环节截止频率的要求。

5结束语

通过对该磁悬浮离心式心脏泵系统刚度与阻尼特性的分析，得出如下结论：

a.径向永磁轴承抑制磁悬浮心脏泵转子径向偏移，增加系统正刚度，能有效提高系统抗干扰能力并降低电磁消耗。

b.在低频段，系统动刚度、阻尼比和固有频率与比例系数显著相关，微分系数近似与系统阻尼比成正比。时间常数增加，阻尼比和固有频率随频率变化稳定性降低。

c.磁悬浮心脏泵转子振动频率为0时，系统动刚度和固有频率与微分系数和时间常数无关，阻尼比与时间常数无关。时间常数为0时，系统阻尼比和固有频率随频率变化，保持恒定。

参考文献：

[1]雷永峰，汪希平. 磁悬浮技术在人工心脏泵中的应用研究. 微特电机，2007(12):4-7.

[2]卢长明. 主动磁悬浮转子刚度、阻尼分析与研究. 武汉:武汉理工大学，2008.

[3]李宏伟，范友鹏，张云鹏，等.轴流式人工心脏泵混合磁悬浮系统的耦合特性. 电机与控制学报，2014，18(5):105-111.

[4]孙玉坤，吴建兵，项倩雯. 基于有限元法的磁悬浮开关磁阻电机数学模型. 中国电机工程学报，2007，27(12):33-40.

[5]曹鑫. 12/8极无轴承开关磁阻电机的研究. 南京:南京航空航天大学，2010.

[6]关勇. 轴流式磁悬浮人工心脏泵磁悬浮系统研究.济南:山东大学，2011.

Abstract:The stiffness and damping of the dynamic characteristics of a centrifugal maglev blood pump, needs to be analyzed. To this end, the equation of radial motion and block diagram of control system about the maglev rotor are provided, according to the study on mechanical characteristics of radial permanent magnetic bearings and switched reluctance motors. And the mathematical expressions of radial stiffness and damping about the maglev system are deduced by combining block diagram of control system and PD controller. Finally, through the simulation example, the characteristic curves of radial stiffness and damping are presented. Studies have shown that dynamic-stiffness coefficients, damping ratio and natural frequency are obviously affected by the link of proportion and filter and derivative coefficient is approximately proportional to damping ratio on low-frequency stage. The study provides theoretical guidance for designing the control system of the centrifugal maglev blood pump and radial displacement control of maglev rotor.

Key words:maglev blood pump；radial permanent magnetic bearings；switched reluctance motors；stiffness；damping

作者简介：李波(1991-)，男，山东济宁人，硕士研究生，研究方向为磁悬浮技术和仪器仪表；孙传余(1982-)，男，山东日照人，讲师，研究方向为仪器仪表。

基金项目：山东省优秀中青年科学家科研奖励基金项目(BS2013NJ015)；黄岛区科技项目(2014-1-39)

收稿日期：2015-09-24

文章编号：1001-2257(2015)12-0027-04

文献标志码:A

中图分类号:TH133.3；R318.11