基于FXLMS算法的主动噪声控制降噪效果研究

王士浩，王生栋，查富生，王鹏飞，李满天

(哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江，哈尔滨 150001)

Noise Attenuation Research of Active Noise Control Based on FXLMS Algorithm

WANG Shihao，WANG Shengdong，ZHA Fusheng，WANG Pengfei，LI Mantian

(State Key Laboratory of Robotic and System ，Harbin Institute of Technology ，Harbin 150001 ，China)



基于FXLMS算法的主动噪声控制降噪效果研究

王士浩，王生栋，查富生，王鹏飞，李满天

(哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江，哈尔滨 150001)

Noise Attenuation Research of Active Noise Control Based on FXLMS Algorithm

WANG Shihao，WANG Shengdong，ZHA Fusheng，WANG Pengfei，LI Mantian

(State Key Laboratory of Robotic and System ，Harbin Institute of Technology ，Harbin 150001 ，China)

摘要：分析了基于FXLMS算法的离线辨识与在线辨识主动噪声控制系统，通过Matlat对系统模型进行建模与仿真，着重比较在线辨识与离线辨识系统模型在稳定性和收敛性等方面的差异，及影响FXLMS算法性能的因素。

关键词：离线辨识；在线辨识；主动噪声控制；FXLMS算法

0引言

在20世纪80年代初，随着数字信号处理理论和技术的逐步成熟，基于自适应滤波器理论的有源噪声控制技术开始起步并迅速发展。Morgan、Widrow及Burgess[1-2]提出了获得广泛应用的滤波-X最小均方FXLMS(filtered-x least mean square)算法。1981年，Burgess率先采用于自适应控制算法对管道噪声的有源控制进行了计算机仿真研究，主动噪声控制的研究证实进入了蓬勃发展的时期。主动噪声控制的对象是发动机排气管道噪声，主要是低于3 000 Hz的低频噪声。查阅文献得知，基于FXLMS算法的ANC系统对低频噪声具有较好的降噪效果。因此，通过Matlat对以FXLMS算法为核心的ANC系统进行仿真分析，了解该算法的优缺点及参数的变化对系统性能的影响。最终确定排气管道主动噪声控制的算法结构及其参数。

1FXLMS算法的辨识模型与仿真

1.1　基于FXLMS算法的次路径辨识模型

在经典的主动噪声控制算法中，需要预先辨识次路径的模型，对次路径特性的估计方法分为2大类，离线辨识和在线辨识。离线辨识，也称离线估计或离线建模，是在控制系统工作之前事先进行次级通道特性估计，具体讲就是单独给次级通道一个激励信号，根据输入输出信号来对其传递特性进行估计。

离线辨识FXLMS算法模型如图1所示。图中S(z)是次级声学路径传递函数模型，Sh(z)是采用离线方式辨识出来的针对S(z)的估计值。

图1　离线辨识的FXLMS算法框图

图2　在线辨识的FXLMS算法框图

从图1和图2可见，在线辨识模型比离线辨识模型多出了用于激励次级路径的白噪声信号，如图2中虚线框所示。这部分就是用于在线获得次路径传递函数的估计值。通过比较可知，在线辨识复杂度明显高于离线辨识，这必将对系统稳定性和收敛性等产生影响，下一节通过仿真来分析。

1.2　基于FXLMS算法的主动降噪控制仿真

参考文献由于声学上的主次路径传递函数是未知的，根据相关来模拟它们的传递函数，设定主次路径传递函数分别为：

P(z)= 0.001+0.005z-1-0.005z-2+0.75z-3+

为了模拟发动机排气管道所具有的低频特性，设置噪声信号由频率分别为50 Hz和100 Hz，幅值均为2的正弦波与最大值为0.2的随机噪声叠加而成。FXLMS算法的滤波器阶数N=32，步长μ=0.001，采样时间为0.000 1 s。

设置总仿真时间为1 s内，在图3所示的仿真结果中，虚线表示采集到的噪声信号yp(k)，点划线表示控制器所产生的反噪声信号ys(k)，实线所代表的残余噪声信号e(k)。在0.16s左右系统实现收敛，也就是系统已经稳定了，没有发散现象产生；稳定后的残差值在0.25左右。

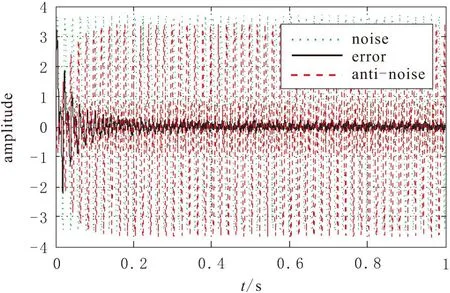
图3　离线辨识的仿真结果

为了能从功率的角度对降噪效果进行评估，采用Spectrum Analyzer对输入的噪声信号和输出的残差信号进行了频谱分析，分析结果如图4所示。从图中可见，残差信号的功率总体上低于输入的噪声信号，而且在频率为50 Hz和100 Hz时，降噪量约为30 dB，降幅最大，说明FXLMS算法对周期性噪声的降噪效果好于随机噪声。

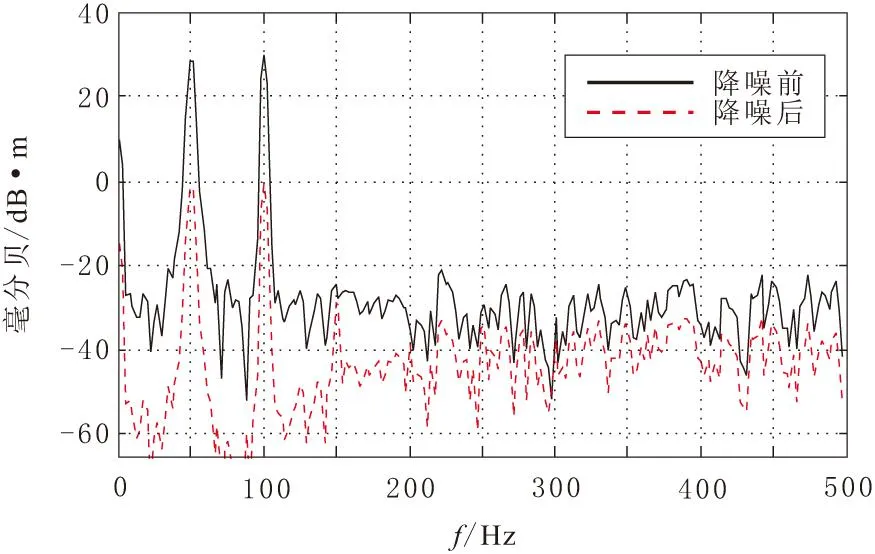
图4　离线辨识的频谱谱分析

根据图2所示的次路径在线辨识的FXLMS算法，在Simulink搭建仿真模型，该模型的构建包含2个核心部分，LMS算法的次路径估计模块和在线辨识的FXLMS算法模块。该模型与理想辨识模型的不同在于通过LMS算法对次路径估计，由于估计误差的存在，系统性能不如理想辨识。这里主次路径传递函数与理想辨识时采用相同值，不同的是这里加入了方差为0.001的高斯噪声对次路径辨识系统充分激励。

在线辨识的仿真结果如图5所示，从图中可以看出，在0.2 s前有2个较大的波动，说明这时次路径的辨识系数误差较大，系统通过权值迭代过程正逐步趋向收敛；在0.2 s之后，系统迅速稳定，残差值在0.9左右。

图5　基于FXLMS算法在线辨识的仿真结果

Spectrum Analyzer对输入噪声信号和输出的残差信号的频谱分析如图6所示。对于50 Hz和100 Hz的正弦波信号降噪量约为13 dB，说明控制算法能够起到较好的降噪效果，但是对于其他频率成分没有明显的效果。

图6　控制前后的频谱分析

从离线辨识与在线辨识模型的主动噪声控制系统对周期性信号和随机噪声叠加信号的降噪效果，可以看出离线的降噪效果明显优于在线辨识，可见正确的模型辨识对系统降噪性能的重要性。由于发动机排气管道模型近似为一个时不变系统。因此，最终确定采用离线辨识的ANC系统来作为实验的依据。此外，系统参数如滤波器阶数、步长也都仿真结果起到很大的作用。

2考虑声反馈的FXLMS算法仿真分析

2.1　声反馈FXLMS算法设计

在前馈ANC系统中，由于声音传播的非单向性，次级声源发出的声音会反馈到参考输入传声器处，导致参考信号失真。通常，这种现象称为次级声反馈(acoustic feedback)。次级声反馈可能导致系统不稳定，在有些情况下需要对其进行补偿。

考虑次级声反馈的前馈ANC系统如图7所示，图中F(z)为次级声反馈路径，引入次级声反馈后，参考传声器测得的信号不再是x(n)，而是叠加了次级反馈声的xc(n)。

图7　考虑次级声反馈的前馈ANC系统

对于次级声反馈的影响，我们可以在算法上予以补偿，由此所形成的算法称为声反馈FXLMS的FBFXLMS(acoustic feedback fXLMS)算法。图8给出了该算法框图。

图8　FBFXLMS算法框图

2.2　考虑声反馈的FXLMS算法ANC系统

根据图8所构建的当次路径估计为离线辨识时的FBFXLMS算法仿真结果如图9和图10所示。设置滤波器的阶数为32，步长为0.001，仿真时间1 s。图2～3为输入噪声信号和输出残差信号的比较图，实线所表示的误差信号在0.2 s左右收敛到稳定值。图10表示的是噪声信号和残差信号的功率谱分析。从图中可以看出针对50 Hz和100 Hz的正弦波噪声大约降低了25 dB，对周期性噪声信号降噪效果明显，而对其它频率成分降噪效果一般。

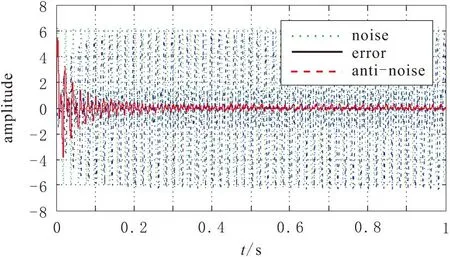
图9　输入噪声信号和输出残差信号的比较

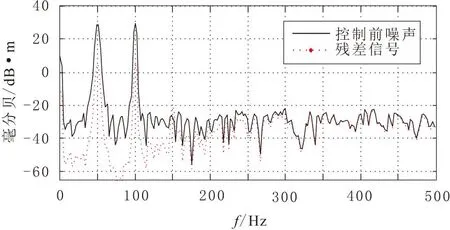
图10　噪声信号和残差信号的功率谱分析

为了能够对FBFXLMS算法中的次路径和次级声反馈路径的模型进行在线辨识，设计了如图11所示的在线辨识FBFXLMS算法。该算法的核心是将次路径和声反馈路径的在线辨识同时融合到系统中，这必将增加系统的复杂度，控制系统的稳定性更易受到影响，但是更加趋近于真实情况。参数设置：2个路径估计模块的LMS算法的步长均为0.001，滤波器阶数为16；FXLMS算法的步长为0.000 1，滤波器阶数为80，仿真步长为0.000 1 s，仿真时间为2 s；输入噪声信号是50 Hz、100 Hz正弦波(幅值均为2)和最大值为0.2的随机噪声的叠加。

图11　在线辨识FBFXLMS算法

对FBFXLMS算法在线辨识的仿真结果进行分析，可以看出，对50 Hz信号的降噪效果较好，降噪量约为8 dB；而对100 Hz周期信号的降噪效果一般，有3 dB左右的降低。从仿真结果可见，添加入声反馈路径和次级路径的估计后，由于收敛速度和计算复杂度等因素的影响。因此，降噪效果远不如理想情况的FBFXLMS算法仿真结果。

3FXLMS算法的性能分析

本节主要分析影响FXLMS算法性能的因素。主要包括自适应滤波器的阶数(滤波器抽头数)和迭代步长μ。此外，ANC系统的结构也对算法的收敛速度和稳定有较大影响。FXLMS算法性能分析时，设定的输入噪声信号为50 Hz、100 Hz正弦波和随机噪声的叠加，幅值分别为1和0.2；仿真步长为0.000 1 s。

当自适应滤波器的阶数设置为N= 32，迭代步长分别取μ= 0.01；μ= 0.001；μ= 0.000 1；μ= 0.000 01时得到仿真过程曲线，误差信号达到稳定状态的时间分别为0.02 s、0.13 s、0.65 s和6.2 s。可见当阶数不变时，随着迭代步长的增加，收敛速度逐渐变慢，且迭代过程的残差逐渐变大。

当迭代步长取μ= 0.001时，自适应滤波器的阶数分别设置为N= 16；N= 64；N= 128；N=256时得到仿真过程曲线。当N取不同值时仿真过程曲线变化不大，选择具有代表性的N=64时的时序图，如图12所示。图中实线所代表的误差信号达到稳定状态的时间都大约在0.1 s左右，说明滤波器阶数不同时系统都能收敛，且收敛速度基本相同。可见当迭代步长不变时，随着滤波器阶数的增加，对收敛速度影响不大，迭代过程的残差有减小的趋势。

图12　μ = 0.001，N=64时仿真图

当迭代步长为 0.01，阶数由 64 增大为128时，发现残差信号发散，系统无法收敛，表明了迭代步长较大时，FXLMS 算法中滤波器阶数对系统的稳定性影响较大；当迭代步长为0.000 1和0.000 01时，收敛速度基本不受滤波器阶数的影响，收敛速度相差不大，且迭代速度较慢。因此，为了实现自适应收敛过程，必须满足FXLMS算法中对步长取值范围的限制条件。

4结束语

首先通过分析得出目前应用最多且性能较好的前馈控制系统是基于FXLMS算法进行的；其次，从理论推导再到仿真分析，总结出离线辨识较在线辨识的FXLMS算法在主动噪声控制系统中具有更好的稳定性和收敛性，降噪效果更好；然后，又对基于FXLMS算法的考虑声反馈估计模型进行了建模与仿真分析，取得了较好的主动降噪效果；最后，对影响FXLMS算法性能的因素进行了分析，得出合适的滤波器阶数和迭代步长是决定主动降噪效果优劣的重要参数，而且这对实验验证等过程具有重要的指导意义。

[1]Morgan D R.An analysis of multiple correlation cancellation loops with a filter in the auxiliary path.Acoustics，Speech and Signal Processing，IEEE Transactions on，1980，28(4)：454-467.

[2]Burgess J C.Active adaptive sound control in a duct：A computer simulation.The Journal of the Acoustical Society of America，1981，70(3)：715-726.

[3]Widrow B，Bilello M.Adaptive inverse control//Proceedings of the IEEE International Symposium ，1993：1-6.

[4]丁庆中.基于次级通道在线辨识的齿轮传动系统振动主动控制研究.重庆：重庆大学，2013.

Abstract：In this paper, the off-line and online identification active noise control systems based on FXLMS algorithm are analyzed; then through MATLAT, modeling and simulation analysis on the system model are conducted; with the focus of research on analyzing the difference of the stability and convergence of the online and offline system models and the factors that impact on the performance of stability and convergence for FXLMS algorithm.

Key words：off-line identification；on-line identification；active noise control；FXLMS algorithm

作者简介：王士浩 (1989 - )，男，满族，河北承德人，硕士研究生，研究方向为机器人技术与系统；王生栋(1989-)，男，山东泰安人，硕士研究生，研究方向为机器人技术与系统；查富生 (1974 - ) ，男，黑龙江哈尔滨人，博士研究生导师，副教授，研究方向为神经网络算法；王鹏飞(1976- ) ，男，黑龙江哈尔滨人，博士研究生导师，副教授，研究方向为微小型机器人；李满天(1974- )，男，黑龙江哈尔滨人，博士研究生导师，教授，研究方向为仿生机器人。

收稿日期：2015-07-01

文章编号：1001-2257(2015)12-0023-04

文献标识码：A

中图分类号：TP242