最大Lyapunov指数在确定混沌系统混沌参数域中的应用

杨琪斌，王　基

(海军工程大学动力工程学院，湖北 武汉 430033)

Application of the Largest Lyapunov Exponent for Confirming Parameter Domain of Chaos System

YANG Qibin，WANG Ji

(College of Power Engineering，Naval University of Engineering，Wuhan 430033，China)



最大Lyapunov指数在确定混沌系统混沌参数域中的应用

杨琪斌，王基

(海军工程大学动力工程学院，湖北 武汉 430033)

Application of the Largest Lyapunov Exponent for Confirming Parameter Domain of Chaos System

YANG Qibin，WANG Ji

(College of Power Engineering，Naval University of Engineering，Wuhan 430033，China)

摘要：非线性振动系统具有与传统线性振动系统不同的某些特点和性能，并且当参数处于一定范围内时，系统将呈现混沌状态。最大Lyapunov指数是判断非线性振动系统是否为混沌的一个重要判据。提出了利用最大Lyapunov指数来确定Duffing系统的混沌参数区间的可行性，并利用参数的分岔图进行验证。

关键词：Duffing系统；Lyapunov指数；参数

0引言

混沌现象是一种确定性的非线性运动。在工程中对混沌现象的利用称之为混沌控制。混沌控制的前提是混沌识别。通过混沌识别确定系统进入混沌状态的参数域是一个非常重要的研究方向，非线性系统的混沌参数域与激励幅值、激励频率等因素密切相关。目前，利用系统运动的相图、功率谱和Poincare映射这三种工具来进行混沌判别应用比较广泛[1-4]。一个系统的最大Lyapunov指数大于零时，系统处于混沌状态。近些年来，Lyapunov的计算方法得到快速发展，1993年，Rosenstein等人基于轨道跟踪法思想，提出了计算最大Lyapunov指数的小数据量法。杨爱波等人使用了基于空间分块的k邻域搜索法。这些算法的出现使得利用Lyapunov指数来进行混沌识别，以确定系统进入混沌状态的参数域成为可能。

1模型的建立

强Duffing模型是一种非常常见和具有代表性的非线性模型，如硬弹簧、钢板弹簧、空气弹簧等，都可以用强Duffing模型来描述其动力特性，在工程中应用非常广泛。因此，强Duffing模型系统混沌特性的参数研究对于混沌控制及其在工程中的应用指导都具有重要意义。

Duffing模型关于参数域的研究主要集中在单参数研究，所谓的单参数研究就是考虑系统运动特性的变化时只改变一个参数变量，而其他参数固定不变。这样可以直观的观察到系统特性随单一参数变化的规律。

非线性振动系统如图1所示，该系统的运动微分方程为：

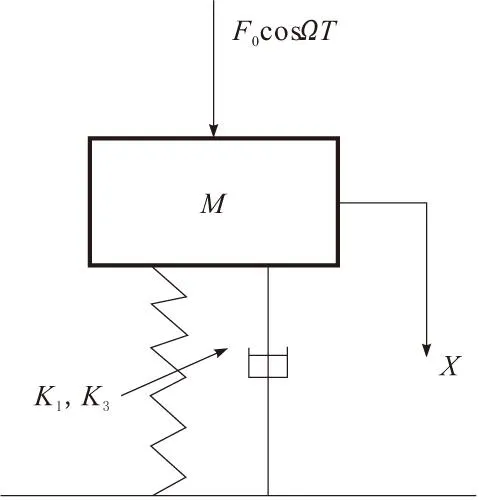
图1　非线性振动系统

(1)

K1X+K3X3为非线性弹性恢复力；K3为负时，系统呈现软特性；K3为正时，系统呈现硬特性。

对方程(1)进行无量纲化处理，得

(2)

(3)

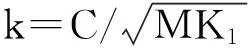
2仿真实验

Duffing系统在没有受外界激励扰动时，处于自激励振荡状态，经过一段时间后趋于稳定状态。要想使系统进入混沌状态，需要对Duffing系统施加外激励。以下仿真研究Duffing系统的不同参数处在哪个区间的时候，系统将处于混沌状态。

2.1　阻尼因子

仿真参数：外激励幅值f=43.00 N；激励频率ω=1.600 rad/s。

系统输出随阻尼因子k变化的分岔图如图2所示，由图可知：k在区间(0.090 0-0.2000)中系统处于混沌状态；k在区间(0.210 0-0.510 0)中系统处于周期三运动；k在区间(0.510 0-1.000 0)中系统处于周期一运动。

最大Lyapunov指数随阻尼因子k变化的关系图如图3所示，由图可知：k在区间(0.900 0-0.200 0)中最大LE大于0，系统处于混沌状态，与分岔图所得结果相同。

图2　输出随阻尼因子k变化的全局分岔图

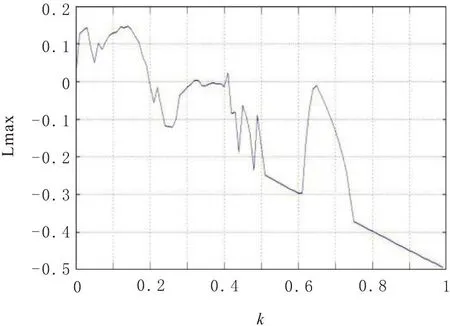
图3　最大LE与阻尼因子的关系

2.2　激励幅值

仿真参数：阻尼因子k=0.100 0；激励频率ω=1.600 rad/s。

输出随激励幅值f变化的分岔图如图4所示，由图可得：f在区间(1.000-23.00)，(56.00-100.0)中系统处于周期一运动；f在区间(23.00-28.00)中系统处于周期二运动；f在区间(28.00-43.00)中系统处于周期三运动；f在区间(43.00-56.00)中系统处于混沌状态。

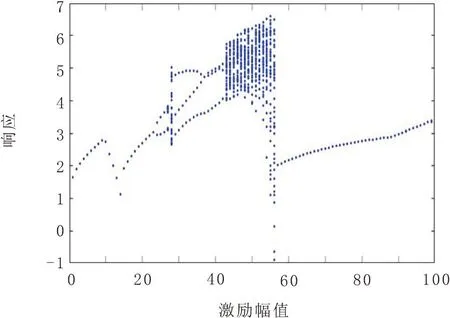
图4　输出随激励幅值f变化的全局分岔图

最大Lyapunov指数随激励幅值f变化的关系如图5所示，由图可得：f在区间(43.00-56.00)中最大LE大于0，系统处于混沌状态。与分岔图所得结果一致。

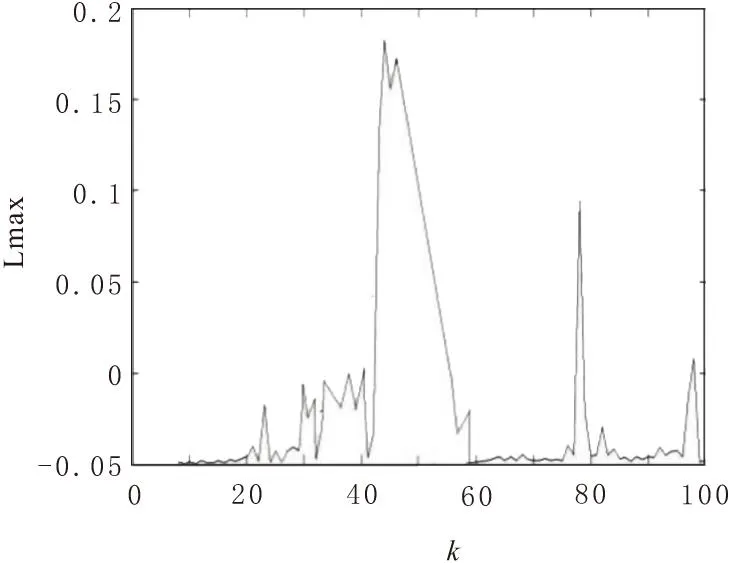
图5　最大LE与激励幅值f的关系

2.3　激励频率

仿真参数：阻尼因子k=0.1000；激励幅值f=43.00N。

输出随激励频率ω变化的全局分岔图如图6所示，由图可得，ω在区间(1.550~1.750)中系统处于混沌状态；在区间(2.000~3.000)中系统处于周期一运动。

图6　输出随激励频率ω变化的全局分岔图

最大Lyapunov指数随激励频率ω变化的关系如图7所示，由图可得，ω在区间(1.550~1.750)中，最大LE大于0，系统处于混沌状态。与分岔图所得结果一致。

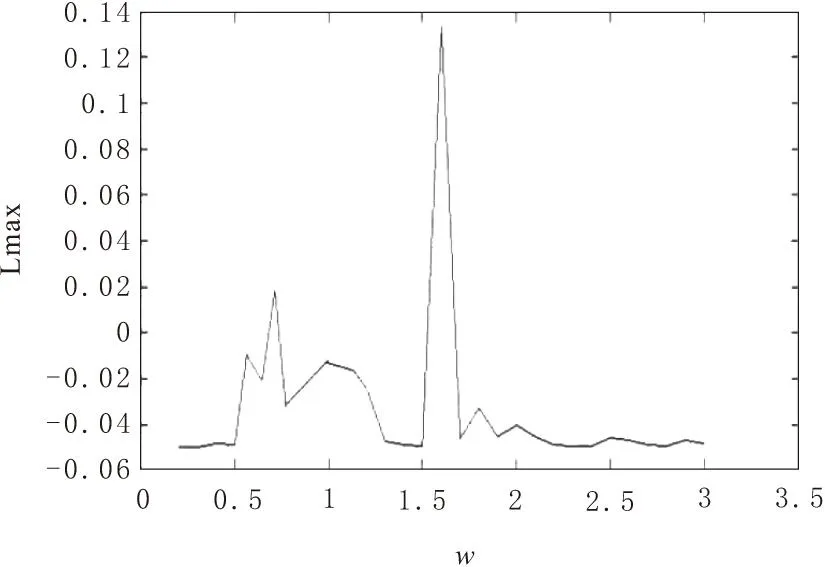
图7　最大LE与激励幅值f的关系

3结束语

在工程中利用混沌现象，需要得到系统进入混沌状态的参数域。近些年来，Lyapunov指数算法得到迅速发展。算法速度和精度的提高，以便利用Lyapunov指数来进行混沌识别，以确定系统进入混沌状态的参数域更加准确，结果更加可信。通过计算硬弹簧Duffing系统的最大Lyapunov指数，得出了系统随着不同参数变化的混沌区间，与利用参数的分岔图得到的混沌系统的混沌参数域一致。证明了利用最大Lyapunov指数确定混沌系统的混沌参数区间是可行的，为利用Lyapunov指数确定任何混沌系统的混沌参数区间提供了一个正确的仿真研究实例。为混沌理论的应用研究提供了一种可靠的数据分析方法，对于混沌控制及其在工程中的应用都具有指导意义。

参考文献：

[1]何四祥．混沌运动在一类非线性结构振动中的数值模拟研究．结构工程师，2007，23 (1) ：43-44．

[2]李卫东，王秀岩．Duffing，模型的仿真分析及混沌控制．大连交通大学学报，2009，30(5)：67-69．

[3]勇俊，郭丽华，吴兴波，等．Matlab在研究非线性混沌中的应用．吉林化工学院学报，2003，20(2)：41-43．

[4]黄胜伟．工程结构混沌振动、混沌最优化算法及其应用．南京：河海大学，2002．

[5]Gencay，Dechert．An algorithm for the n-dimensional unknown dynamical system．Physica D，1992，59：142-157．

[6]Senstein M T R，Collins J J，Deluca C J.A practical method for calculating largest Lyapunov exponents from small data sets.Physica D，1993(65)：117-134.

[7]杨爱波，王基，刘树勇，等.基于空间栅格法的最大Lyapunov指数算法研究.电子学报，2012，40(9)：1871-1875.

[8]汪新明．橡胶隔震支座的非线性建模及参数识别研究．南京：南京航空航天大学，2008.

Abstract：Nonlinear vibration systems have some characteristics and properties different from traditional linear vibration systems. When the parameter is in some ranges, the system is in a chaotic state. The largest Lyapunov exponent is an essential criterion to judge whether the system is in chaos state or not. The feasibility of using the Largest Lyapunov exponent to confirm the parameter domain is presented in this paper, and it is verified by the bifurcation diagram of system.

Key words：duffing system；lyapunov exponent；parameter

作者简介：杨琪斌(1991-)，男，河北石家庄人，硕士研究生，研究方向为机械动力学和非线性振动。王基(1964-)，男，湖北武汉人，副教授，硕士研究生导师，研究方向为机械动力学和非线性振动。

基金项目：国家自然科学基金(5157090314)；海洋工程国家重点实验室(上海交通大学)开放课题(1009)

收稿日期：2015-09-14

文章编号：1001-2257(2015)12-0003-03

文献标识码：A

中图分类号：O322