多分辨分析和K均值聚类改进FCM图像分割

郭海涛1,2,赵红叶3,徐　雷3，侯一民3，焦圣喜3

(1.内蒙古大学电子信息工程学院,内蒙古 呼和浩特 010021;2.东北电力大学电气工程学院,

吉林 吉林 132012;3.东北电力大学自动化工程学院,吉林 吉林 132012)



多分辨分析和K均值聚类改进FCM图像分割

郭海涛1,2,赵红叶3,徐雷3，侯一民3，焦圣喜3

(1.内蒙古大学电子信息工程学院,内蒙古 呼和浩特 010021;2.东北电力大学电气工程学院,

吉林 吉林 132012;3.东北电力大学自动化工程学院,吉林 吉林 132012)

摘要：模糊 C 均值(Fuzzy C-Means,FCM)聚类广泛应用于图像分割,但FCM聚类中随机确定初始聚类中心容易导致图像的错误分割.为了避免这个缺点,提出一种用于图像分割的FCM聚类初始聚类中心的选取方法.该方法利用图像灰度-邻域均值二维直方图的峰值的个数确定图像聚类数目，然后对图像的低频子带图像利用K均值聚类得到FCM聚类初始聚类中心.实测图像的分割实验表明该方法具可行性.

关键词：二维直方图;多分辨分析;K均值聚类;FCM聚类;图像分割

模糊C均值(Fuzzy C-Means，FCM)聚类[1]因具有无需训练样本、无监督性、能够实现多区域分割等特点,被广泛应用于图像分割领域[2-7].FCM聚类中初始聚类中心是随机选取的.随机选取初始聚类中心有时会导致错误的聚类,因而导致错误的图像分割.笔者提出一种用于图像分割的FCM聚类初始聚类中心的选取方法.该方法的步骤是:(ⅰ)利用图像的灰度-邻域均值二维直方图(简称二维直方图)[3]的峰值的个数确定图像聚类的数目(分割的区域数目);(ⅱ)对图像进行小波多分辨分析得到低频子带图像;(ⅲ)对低频子带图像利用K均值聚类(用步骤(ⅰ)中得到的聚类数目)得到FCM聚类的初始聚类中心.

利用上述初始聚类中心选取方法获得图像的FCM聚类初始聚类中心后,再利用FCM聚类(用步骤(ⅰ)中得到的聚类数目)重新对原图像聚类得到分割后的图像.下文阐述FCM聚类初始聚类中心的选取方法和完整的FCM聚类分割过程,并以实际的声呐图像为例给出文中方法的实验结果,同时将文中方法与其他常用方法的实验结果进行对比.

1图像FCM聚类初始聚类中心选取方法

利用图像二维直方图[3]的峰值的个数确定图像聚类数目，然后对图像的低频子带图像利用K均值聚类得到FCM聚类初始聚类中心.下面介绍用于获得聚类数目的二维直方图和用于获得低频子带图像的小波多分辨分析[8].关于K均值聚类可参考相关的文献.

1.1 二维直方图

以每个像素周围的8个像素作为一个邻域,计算其邻域灰度均值.设原始图像有L个灰度等级,nij为图像中灰度值为i而邻域灰度均值为j的像素点数,M，N分别为图像的行数和列数,则pij(i,j=1,2,…,L)就是该图像的灰度-邻域均值二维直方图[3]：

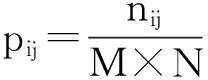
二维直方图由于同时考虑了像素灰度值和像素邻域灰度均值,因此它比灰度直方图的抗干扰性强.在二维直方图中目标和背景更容易区分[3].

1.2 图像的小波多分辨分析

对二维图像信号f(x,y)进行小波变换后,可以将信号分解为1个低频子带和3个高频子带,其中低频子带包含了图像的概貌，3个高频子带包含了图像在水平方向、垂直方向和对角方向上的细节[8].在变换的每一层次,图像都被分解为4个1/4大小的图像,它们都是由原图像与一个小波基的内积后,再经过在行和列方向进行2倍的间隔抽样而生成的.图像尺寸变为上一层的1/4[9].若要对二维图像信号f(x,y)进行2层小波分解,则可以在完成1层分解后,在低频子带上进行小波变换,得到2层分解.

2基于FCM聚类的图像分割

2.1 FCM聚类算法

FCM聚类算法如下[1,10]：

设数据集X={x1,x2,…,xN}为待分类对象,c(c>1)为分类数目,vi为第i(i=1,2,…,c)类类心,uij为第j(j=1,2,…,N)个对象属于第i类的隶属度.定义FCM聚类的目标函数为[1,10]

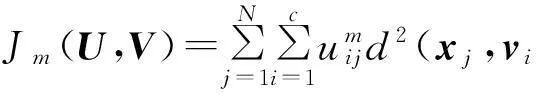
目标函数Jm(U,V)的约束条件为

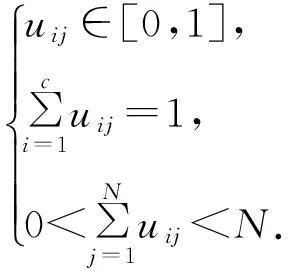
(1)

其中:d2(xj,vi)为xj与vi之间的欧氏距离;m为模糊加权指数,m>1;V为聚类中心集,V={v1,v2,…,vc};U为模糊矩阵,U=(uij)c×N.

利用拉格朗日乘数法则,可以求得在(1)式的约束下使目标函数Jm(U,V)取极小值的必要条件为[1,10]

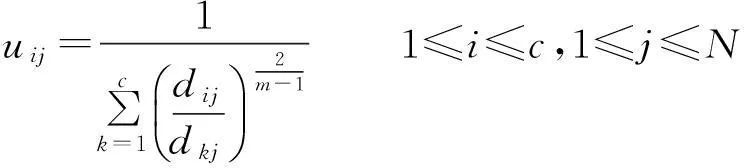
(2)

(3)

目标函数Jm(U,V)的极小值，是根据二维直方图确定的聚类数目c和K均值聚类确定的初始聚类中心通过(2)和(3)式的迭代完成的.迭代时可以事先指定模糊矩阵U的一个范数或最大迭代次数作为迭代终止条件.具体迭代步骤见参考文献[1,10].

2.2 FCM聚类图像分割的步骤

利用FCM聚类分割图像时,初始聚类中心利用K均值聚类确定,聚类数目利用图像二维直方图[3]的峰值的个数确定(即与确定初始聚类中心的K均值聚类的聚类数目一致).FCM聚类图像分割步骤如下:

(ⅰ)计算滤波后图像的二维直方图；

(ⅱ)对二维直方图进行3×3均值滤波；

(ⅲ)由均值滤波后的二维直方图峰值的个数确定图像K均值聚类和FCM聚类的聚类数目；

(ⅳ)对滤波后的图像进行小波多分辨分析,得到低频子带图像；

(ⅴ)利用K均值聚类得到低频子带图像的聚类中心，将其作为FCM聚类的初始聚类中心；

(ⅵ)设定模糊加权指数m；

(ⅶ)根据(2)式计算初始隶属度uij；

(ⅷ)设定迭代运算中止的最大迭代次数；

(ⅸ)按2.1节和参考文献[1,10]中的方法进行迭代运算(即聚类)；

(ⅹ)去除聚类后图像中的除孤立区和孔得到分割后的图像.

3实例分析

图1来源于文献[11],是一幅海底目标的合成孔径声呐图像,图像尺寸为152120.图1大部分为海底混响区,该部分构成图像的背景.图1中较突出的部分为目标区.目标区中较亮的部分是目标亮区，与之相邻(右侧)的较暗区域是目标暗区.图2和3分别为中值滤波(3×3)和均值滤波(3×3)后的图像.图4为图3的二维直方图,图4经过均值滤波(3×3)后得到图5.比较图4和图5可以看出，利用图5确定图像聚类数目可以避免虚假峰值的干扰.

根据图5可知,聚类数目为3.对图3利用db1小波进行2层小波分解,得到图6.对于图6,利用K均值聚类得到FCM聚类的初始聚类中心;取m=2[10],最大迭代次数为100.聚类后得到图7(未去除孤立区和孔,下文同).作为与文中方法的比较,这里给出最为常用的多阈值Otsu法[12]的阈值化结果(图8)，阈值为50和200.

从图7和图8可以看出,双阈值Otsu法分割出的目标亮区比实际情况偏小,文中算法分割出的目标亮区和目标暗区的大小、形状更接近实际情况,分割结果更准确.

图1　原始图像　　　　　　　　图2　图1中值滤波后　　　　　　图3　图2均值滤波后

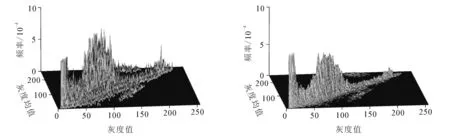
图4　图3的二维直方图　　　　　　　　　　　　　　　　　图5　图4均值滤波后

图6　图3的2层小波分解　　　　　　图7　文中方法聚类　　　　　　　　图8　双阈值Otsu法

4结语

针对图像FCM聚类时随机确定初始聚类中心容易导致图像错误分割的问题,提出一种用于图像分割的FCM聚类初始聚类中心的选取方法,并进而形成一种图像FCM聚类分割的改进方法.以某海底目标的合成孔径声呐图像为例,给出了详尽的分割过程.实测图像的分割实验表明文中方法具有可行性.该方法适用于目标亮区、目标暗区、海底混响区的面积相差不是很悬殊的情况.另外,该方法也存在一些需要进一步改进的地方,比如:利用二维直方图确定聚类数目存在一定的误差,有时会导致错误的结果;用于确定FCM聚类初始聚类中心的K均值聚类有时会陷入局部最小,这有可能使得其确定的FCM聚类初始聚类中心不是最合适的.

参考文献：

[1] BEZDEK J C,EHRLICH R,FULL W.FCM:The Fuzzy C-Means Clustering Algorithm[J].Computers & Geosciences,1984,10(2):191-203.

[2] 郭海涛,刘丽媛,赵亚鑫,等.基于MAR与FCM聚类的声呐图像分割[J].仪器仪表学报,2013,34(10):2 322-2 327.

[3] 刘健庄.基于二维直方图的图象模糊聚类分割方法[J].电子学报,1992,20(9):40-46.

[4] THAMARAICHELVI B,YAMUNA G,VANITHA U.An Improved Method of Image Segmentation Using Fuzzy C-Means[C].Proceedings of 2012 IEEE International Conference on Advances in Engineering,Science and Management,Tamil Nadu.New York:IEEE,2012:669-672.

[5] QIU Cunyong,XIAO Jian,YU Long,et al.A Modified Interval Type-2 Fuzzy C-Means Algorithm with Application in MR Image Segmentation[J].Pattern Recognition Letters,2013,34(12):1 329-1 338.

[6] FENG Jie,JIAO L C,ZHANG Xiangrong,et al.Robust Non-Local Fuzzy C-Means Algorithm with Edge Preservation for SAR Image Segmentation[J].Signal Processing,2013,93(2):487-499.

[7] 崔兆华,张萍,李洪军,等.融合结构特征的增强型FCM图像分割算法[J].东北大学学报:自然科学版,2013,34(7):922-926.

[8] 杨佐龙,王新超,贾明.基于小波域双阈值分割的SAR图像预处理方法[J].船舶电子对抗,2013,36(1):62-65.

[9] 袁蔚林,马燕,刘圣伟,等.基于小波变换及Matlab的遥感图像压缩效果分析[J].地理信息世界,2013,20(3):39-44.

[10] 郭桂蓉.模糊模式识别[M].长沙:国防科技大学出版社,1992:173-180.

[11] GROEN J,HANSEN R E,CALLOW H J,et al.Shadow Enhancement in Synthetic Aperture Sonar Using Fixed Focusing[J].IEEE Journal of Oceanic Engineering,2009,34(3):269-284.

[12] 苟中魁,张少军,李忠富,等.一种Otsu阈值法的推广——Otsu双阈值法[J].机械,2004,31(7):12-14.

(责任编辑向阳洁)

Improved FCM Image Segmentation Based on Multi-Resolution

Analysis and K-Means Clustering

GUO Haitao1,2,ZHAO Hongye3,XU Lei3,HOU Yimin3,JIAO Shengxi3

(1.College of Electronic Information Engineering,Inner Mongolia University,Hohhot 010021,China;2.College of

Electrical Engineering,Northeast Dianli University,Jilin 132012,Jilin China;3.College of

Automation Engineering,Northeast Dianli University,Jilin 132012,Jilin China)

Abstract:The fuzzy C-Means (FCM) clustering is widely used in image segmentation,but the random determination of initial clustering centers of the FCM clustering is likely to generate incorrect segmentation of an image.To avoid the such deficiency,a method of choosing initial clustering centers in the FCM clustering for image segmentation is proposed.The method determines the number for the image clustering by means of the number of the peaks in the two-dimensional histogram of an image comprised of gray values of pixels and mean values of their neighborhoods.Then the K-means clustering is used to obtain the initial clustering centers of the FCM clustering for the low-frequency subband image of the original image.The image segmentation experiments show that the proposed method is feasible.

Key words:two-dimensional histogram;multi-resolution analysis;K-means clustering;FCM clustering;image segmentation

作者简介：郭海涛(1965—)，男，黑龙江安达人，内蒙古大学电子信息工程学院教授，博士，主要从事图像处理、模式识别等研究.

基金项目：国家自然科学基金资助项目(41076060)；吉林省自然科学基金资助项目(20130101056JC)；内蒙古自然科学基金资助项目(2014MS0601)；内蒙古大学高层次人才引进科研项目(135123)

收稿日期：2014-09-05

中图分类号：TP391.4

文献标志码：A

DOI:10.3969/j.issn.1007-2985.2015.02.007

文章编号：1007-2985(2015)02-0029-04