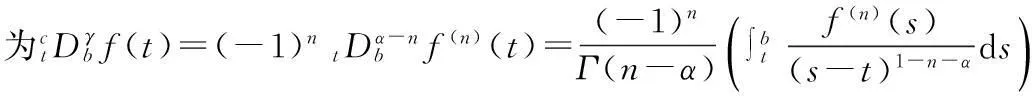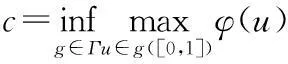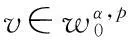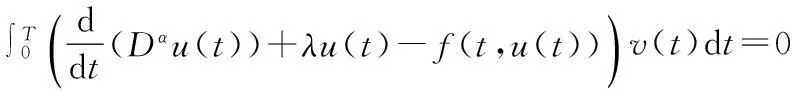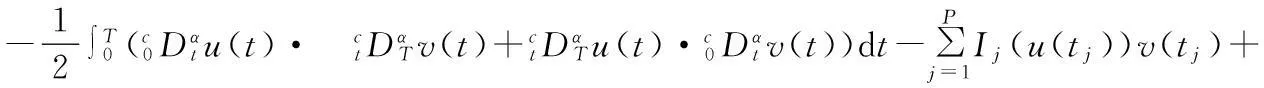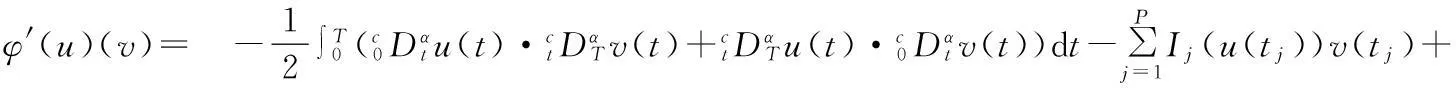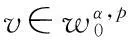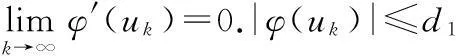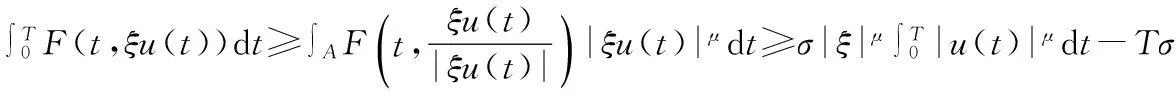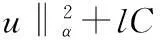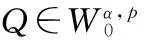分数阶脉冲微分方程边值问题解的存在性
黄 羿,陈国平
(吉首大学数学与统计学院,湖南 吉首 416000)
分数阶脉冲微分方程边值问题解的存在性

黄羿,陈国平
(吉首大学数学与统计学院,湖南 吉首 416000)
摘要:运用临界点理论中的山路引理,研究一类具有狄利克雷边值问题的分数阶脉冲微分方程解的存在性,证明了解的存在性结果.
关键词:脉冲;分数阶;微分方程;狄利克雷边值条件;临界点理论
作为整数阶微分方程的推广,分数阶微分方程用来描述复杂物理和动力学问题时,可以更加准确地描述非线性非保守的动力学行为.同时,分数阶微积分的全局相关性可以更优美地刻画现实世界中的现象和规律[1-4].因而,近几十年来,分数阶微积分被广泛地应用于生物、物理、电子、工程及控制论等领域[5-9].目前,关于分数阶微分方程的研究包括解的存在性和唯一性、解的稳定性、边值问题等解的动力学性质[10-14],主要研究方法包括不动点定理、拓扑度理论(延拓定理和重合度理论)、比较方法(上下解方法和单调迭代方法)和临界点理论[5,11,15-21].脉冲微分方程能够充分考虑到瞬时突变现象对状态的影响,更深刻、精确地反映事物的变化规律,具有很强的现实意义[22-23],在医学、生物、控制论及航天运动模型中广泛存在[24-27].
2012年,文献[16]首先使用临界点理论研究分数阶微分方程解的存在性,事实证明这种方法对于解决带左右分数阶导数算子的物理模型非常有效.据了解,运用临界点理论解决分数阶脉冲微分方程边值问题解的存在性的文献鲜少出现.笔者尝试使用临界点理论中的一般山路引理,研究下列分数阶脉冲微分方程方程边值问题解的存在性:

(1)

1预备知识
定义1[1]设函数f∈ACn([a,b],RN),当n-1≤α 函数的α阶Riemann-Liouville右导数为 定义2[1]设函数f∈ACn([a,b],RN),当n-1≤α 为了使用方便,引入分数阶导数的几点性质,其中f(t)和g(t)为函数,α和μ为常数[2]. 性质1Dαμ(f(t)+g(t))=Dαμf(t)+Dαμg(t). 定义3[5]设E是一个实Banach空间,F是E上具有连续Frechet微分的泛函,即F∈C1(E,R).如果对于∀{un}⊂E,{F(un)}有界且F′(un)→0(n→∞),蕴含{un}在E中存在收敛的子序列,那么称泛函F在E上满足Palais-Smale条件(简称为PS条件). 定义范数 (2) (3) 联立(2),(3)式,得 (4) 其中 (5) 则泛函φ可导.由性质1和性质2知 (6) 从而函数u是分数阶脉冲边值问题(1)的一个弱解. 2主要结果及证明 定理2假设以下条件成立: (H1)F∈C([0,T]×RN,R),存在μ∈[0,1/2),M>0,使得对∀x∈RN,当|x|≥M,M>0,t∈[0,T]时,有0 (H2)[23]f是次线性的,即存在常数a>0,b>0和γ∈[0,1),使得对∀(t,x)∈[0,T]×R有|f(t,x)|≤a+b|x|r. (H3)[23]脉冲函数次线性增长,即存在常数aj>0,bj>0和γj∈[0,1),使得对∀x∈R,有|Ij(x)|≤aj+bj|x|γj(j=1,2,…,p). 当α∈(1/2,1]时,分数阶脉冲边值问题(1)至少有1个解. 首先引入几个重要的引理: 引理4[28]假设条件(H1)成立,对∀t∈[0,T],下列结论成立: 然后考虑α∈(1/2,1]时,分数阶脉冲边值问题(1)解的存在性. 第1步:验证φ(uk)满足(PS)条件. 从而知φ(uk)满足(PS)条件. 第2步:用临界点理论证明脉冲边值问题(1)的弱解存在. 由引理4知, 参考文献: [1]KILBASAA,RIVASTAVAM,TRUJILLOJJ.TheoryandApplicationsofFractionalDifferentialEquations[M].Amsterdam:ElsevierScienceLtd.,2006. [2]IGORPODLUBNY.FractionalDifferentialEquations[M].NewYork:AcademicPress,1999. [3] 周燕.分数阶Pfaff-Birkhoff变分问题及其对称性[D].苏州:苏州科技学院,2013. [4] 王小东.Riemann-Liouvlle分数阶微积分及其性质证明[D].太原:太原理工大学,2008. [5]RABINOWITZPH.MinimaxMethodsinCriticalPointTheorywithApplicationtoDifferentialEquations[M].American:AmericanMathematicalSociety,1986. [6]MAGINRL.FractionalCalculusinBioengineering[M].Redding,CT:BegellHouseInc.,2006. [7]VASILLYETARASOV.分数维动力学:分数阶积分在粒子,场及介质动力学中的应用[M].北京:高等教育出版社,2010. [8] 孙文,孙宏广,李西成.力学与工程问题的分数阶导数建模[M].北京:科学出版社,2010. [9] 汪纪峰.分数阶系统控制性能分析[M].北京:电子工业出版社,2010. [10]RAVIPAGARWAL,BASHIRAHMAD.ExistenceTheoryforAnti-PeriodicBoundaryValueProblemsofFractionalDifferentialEquationsandInclusions[J].ComputersandMathematicswithApplications,2011,62(3):1 200-1 214. [12]GUOTianliang,JIANGWei.ImpulsiveProblemsforFractionalDifferentialEquationswithBoundaryValueConditions[J].ComputersandMathematicswithApplications,2012,64(10):3 281-3 291. [13]CHENYi,TANGXianhua.SolvabilityofSequentialFractionalOrderMulti-PointBoundaryValueProblemsatResonance[J].AppliedMathematicsandComputation,2012,218(14):7 638-7 648. [14]MUJEEBURREHMAN,PAULWELOE.ExistenceandUniquenessofSolutionsforImpulsiveFractionalDifferentialEquations[J].AppliedMathematicsandComputation,2013,224(1):422-431. [15]LIJianli,LUOZhiguo,YANGXuxin,etal.MaximumPrinciplesforthePeriodicBoundaryValueProblemforImpulsiveIntegro-DifferentialEquations[J].NonlinearAnalysis,2010,72(9/10):3 837-3 841. [16]JIAOFeng,ZHOUYong.ExistenceofSolutionsforaClassofFractionalBoundaryValueProblemsviaCriticalPointTheory[J].ComputersandMathematicswithApplications,2011,62(3):1 181-1 199. [17]JIAOFeng,ZHOUYong.ExistenceResultsforFractionalBoundaryValueProblemviaCriticalPointTheory[J].InternationalJournalBifurcationandChaos,2012,22(4):1 250 086-1 250 103. [18]SUNHongrui,ZHANGQuanguo.ExistenceofSolutionsforaFractionalBoundaryValueProblemviatheMountainPassMethodandanIterativeTechnique[J].ComputersandMathematicswithApplications,2012,64(10):3 436-3 443. [19]CHENFulai.CoincidenceDegreeandFractionalBoundaryValueProblemswithImpulses[J].ComputersandMathematicswithApplications,2012,64(10):3 444-3 455. [20]HUChaozhu,LIUBin,XIESongfa.MonotoneIterativeSolutionsforNonlinearBoundaryValueProblemsofFractionalDifferentialEquationwithDeviatingArguments[J].AppliedMathematicsandComputation,2013,222(1):72-81. [21]JIAMei,LIUXiping.MultiplicityofSolutionsforIntegralBoundaryValueProblemsofFractionalDifferentialEquationswithUpperandLowerSolutions[J].AppliedMathematicsandComputation,2014,232(1):313-323. [22]JUANJNIETO,DONALO’REGAN.VariationalApproachtoImpulsiveDifferentialEquations[J].NonlinearAnalysis:RealWorldApplications,2009,10(2):680-690. [23] 白亮.基于临界点理论的脉冲边值问题解答存在性及多解性[D].长沙:中南大学,2012. [24]AKHMETOVMU,ZAFERA.ControllabilityoftheVallee-PoussinProblemforImpulsiveDifferentialSystems[J].JournalofOptimizationTheoryandApplication,1999,10(2):263-276. [25]PEIYongzhen,LIChangguo,WANGChunhua.ComplexDynamicsofOne-PreyMulti-PredatorSystemwithDefensiveAbilityofPreyandImpulsiveBiologicalControlonPredators[J].AdvancesinComplexSystems,2005,8(4):483-495. [26]PRADOAFBA.Bi-ImpulsiveControltoBuildaSatelliteConstellation[J].NonlinearDyn.Syst.Theory,2005,5:169-175. [27]DAIBinxiang,SUHua,HUDianwang.PeriodieSolutionofaDelayedRatio-DependentPredator-PreyModelwithMonotonieFunctionalResponseandImpulse[J].NonlinearAnalysisTMA,2009,70(1):126-134. [28]ZHANGZiheng,YUANRong.AnApplicationofVariationalMethodstoDirichletBoundaryValueProblemwithImpulses[J].NonlinearAnalysis:RealWorldApplications,2010,11:155-162. (责任编辑向阳洁) Existence of Solutions for Boundary Value Problems of Impulsive Fractional Differential Equations via Critical Point Theory HUANG Yi,CHEN Guoping (College of Mathematics and Statistics,Jishou University,Jishou 416000,Hunan China) Abstract:In this paper,we investigate existence results of Dirichlet boundary problems for a class of impulsive fractional differential equations.The arguments are based upon the mountain pass theorem of critical point theory. Key words:impulsive;fractional;differential equations;Dirichlet boundary conditions;critical point theory 作者简介:黄羿(1982—),女,湖南岳阳人,吉首大学数学与统计学院讲师,硕士生,主要从事微分方程与动力系统研究;陈国平(1964—),男,湖南邵阳人,吉首大学数学与统计学院教授,博士,主要从事微分方程与动力系统研究. 基金项目:湖南省教育厅科学研究项目(14C0940) 收稿日期:2014-10-18 中图分类号:O175.8 文献标志码:A DOI:10.3969/j.issn.1007-2985.2015.02.003 文章编号:1007-2985(2015)02-0011-05