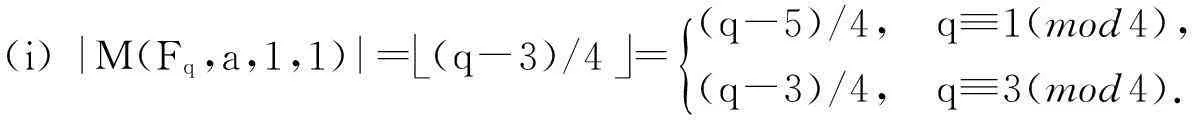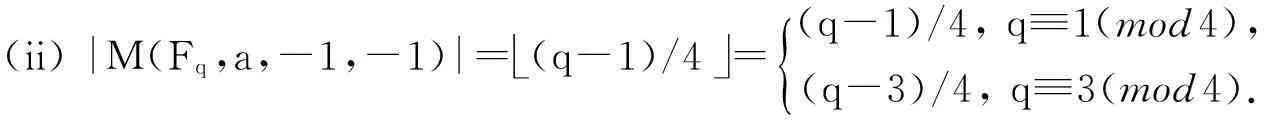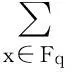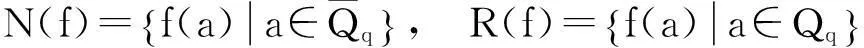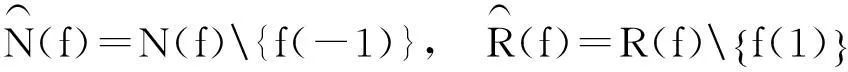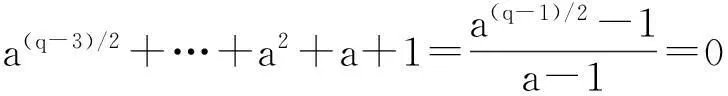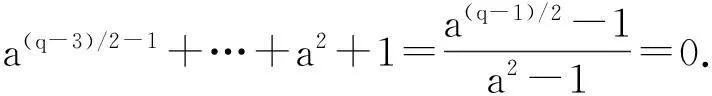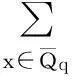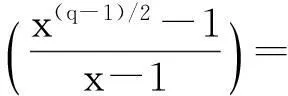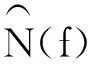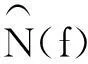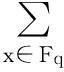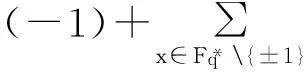有限域上的二次特征与多项式的值集

昝海侠，　曹　炜

(宁波大学数学系，宁波315211)



有限域上的二次特征与多项式的值集

昝海侠，曹炜

(宁波大学数学系，宁波315211)

[摘要]利用有限域Fq上的二次特征，研究了几类特殊多项式在q≡±1(mod4)时的值集.

[关键词]二次剩余； 二次特征； 多项式的值集

1引言

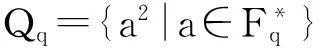
二次非剩余集合为

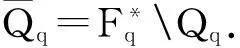
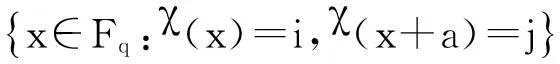
设多项式f(x)∈Fq[x]，则f(x)诱导出一个Fq→Fq的映射：xf(x). 像f(Fq)又称为f(x)的值集；当f(Fq)=Fq时，f(x)叫做置换多项式. 值集是有限域的重要研究对象. 本文将利用Fq上的二次特征，结合孙智宏、郭嵩等人的结果，研究几类特殊多项式的值集.

2引理

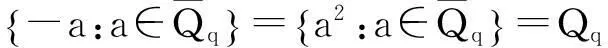
文献[2]给出了M(Fq,a,i,j) 的构造.

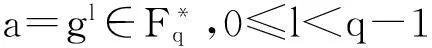
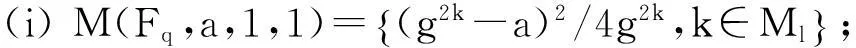
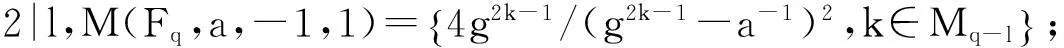
其中

Ms=i:s/2+1≤i≤(2s+q-3)/4{},0≤s<(q-1)/2,MS-(q-1)/2,(q-1)/2≤s

需要指出的是，文献[2]中关于M(Fq,a,-1,1)和M(Fq,a,1,-1)的讨论并不完整，因为它不仅与l的奇偶性有关，还与q≡±1(mod4)有关. 但本文更关心的是M(Fq,a,i,j)的大小，由上述引理及文献[2]中的方法，可以得到以下结论:

引理2.3当a=±1时，有

(i)|M(Fq,a,1,1)|=(q-3)/4=(q-5)/4,q≡1(mod4),(q-3)/4,q≡3(mod4).{

(ii)|M(Fq,a,-1,-1)|=(q-1)/4=(q-1)/4,q≡1(mod4),(q-3)/4,q≡3(mod4).{

引理2.4当a=±1,q≡1(mod4)时，有

|M(Fq,a,-1,1)|=|M(Fq,a,1,-1)|=(q-1)/4.

引理2.5当q≡3(mod4)时，有

|M(Fq,-1,-1,1)|=|M(Fq,1,1,-1)|=(q+1)/4,

|M(Fq,-1,1,-1)|=|M(Fq,1,-1,1)|=(q-3)/4.

2主要结论及其证明

对任意的f(x)∈Fq[x]，定义

特别地，当q≡3(mod4)时，定义

定理3.1(i)a∈Qq⟺a为x(q-3)/2+…+x2+x+1的根，或a=1.

(ii) 若q≡1(mod4)，则a∈Qq⟺a为x(q-3)/2-1+…+x2+1的根，或a=±1．

定理3.2设f(x)=x(q-3)/2+…+x2+x+1，则

(i) 当q≡1(mod4)时，N(f)中二次剩余和二次非剩余的个数相等.

(ii) 当q≡3(mod4)时，N(f)中二次剩余和二次非剩余的个数相差1；具体地

因此只须考察集合M(Fq,-1,-1,-1)和M(Fq,-1,-1,1)的大小.

(i) 当q≡1(mod4)时，由引理2.3和引理2.4知

|M(Fq,-1,-1,-1)|=|M(Fq,-1,-1,1)|=(q-1)/4.

因此N(f)中二次剩余和二次非剩余的个数相等.

(ii) 当q≡3(mod4)时，由引理2.3和引理2.5知

|M(Fq,-1,-1,-1)|=(q-3)/4,|M(Fq,-1,-1,1)|=(q+1)/4,

推论3.3设f(x)=1-x+x2-x3+…+(-x)(q-3)/2，则

(i) 当q≡1(mod4)时，N(f)中二次剩余和二次非剩余的个数相等.

|M(Fq,-1,1,-1)|=|M(Fq,-1,1,1)|=(q-3)/4.

[参考文献]

[1]Sun Z H. Consecutive Numbers with the Same Legendre Symbol [J]. Proc. Amer. Math. Soc. 2002, 130: 2503-2507.

[2]Guo Song. A note on quaduatic character over fininte fields [J]. Nanjing Univ. J. Math. Biquarterly. 2006, 23(1): 114-120.

Quadratic Characters and Value Sets of Polynomials over Finite Fields

ZANHai-xia，CAOwei

(Department of Mathematics，Ningbo University，Ningbo ,Zhejiang 315211,China)

Abstract:Utilizing the quadratic character over the finite field Fq， we study the value sets of polynomials for q≡±1(mod4) respectively.

Key words:quadratic character； quadratic residue； value set of polynomial

[中图分类号]O156.1

[文献标识码]A

[文章编号]1672-1454(2015)05-0020-03

[基金项目]宁波市自然科学基金(2014A610017)

[收稿日期]2015-06-09