一类NLSE方程的精确行波解*



一类NLSE方程的精确行波解*

高芳，马锐，熊梅

(云南财经大学 统计与数学学院，昆明 云南 650021)

摘要：通过行波变换将一类非线性薛定谔方程及其推广形式转化为常微分方程动力系统，求出其奇点，并讨论其类型；计算出系统的哈密尔顿量，并运用Maple软件，画出了系统的奇点和相图；求出动力系统的解，并回代求出非线性偏微分方程及其推广形式的精确行波解.

关键词：非线性薛定谔方程;推广形式;动力系统;哈密尔顿量;行波解

1非线性薛定谔方程

非线性薛定谔方程(Nonlinear Schrödinger Equation,NLSE)或方程组在数学和物理学研究中具有广泛的应用[1-2].近年来，因其在海洋研究中的地位而变得十分有意义，人们对如下的非线性薛定谔方程[3]讨论较多：

(1)

其中x是传播距离，t是转化变量.应用行波法，Akhmediev N等[4]求解出方程的怪波解.本文运用动力系统行波法[5-8]及Maple软件求解该非线性薛定谔方程及其推广形式的精确行波解.

1.1非线性薛定谔方程的行波变换

为了找出此非线性薛定谔方程(NLSE)的解，设[6]

φ(x,t)=eiη·u(ξ)

其中，ξ=x-ct,η=px+qt.为了简便起见，将u(ξ)简写为u.

由假设，可以推出

将上式代入(1)式后，分离实部和虚部，分别令实部和虚部为零，可得系统

由系统的第一个式子，可知

uξ=0或1-qc=0

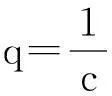
1.2动力系统

由上述系统的第二个方程，移项得

这是一个微分动力系统，将动力系统中的两个式子相除，并变量分离后积分得到

c1是积分常数，通常令c1=0,可得

(2)

由(2)式，得到一个哈密尔顿量

(3)

1.3奇点类型

在奇点A(0,0)时，有λ2-a=0.

(ii)当a<0,b<0时，λ1,2为两虚根，此时A(0,0)为中心(如图2所示).

图1　a>0,b<0时奇点的情况　　　　　　　　　　　 　 图2　a<0,b<0时奇点的情况

1.4结果分析

(1)当a<0,b<0时，A(0,0)为中心，由(3)式可以得到

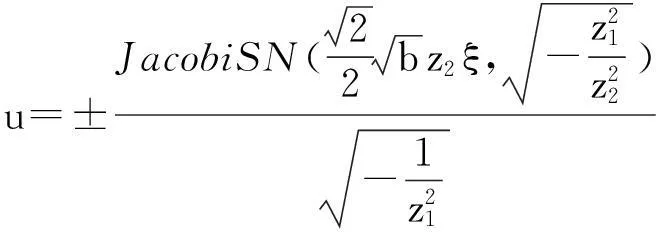
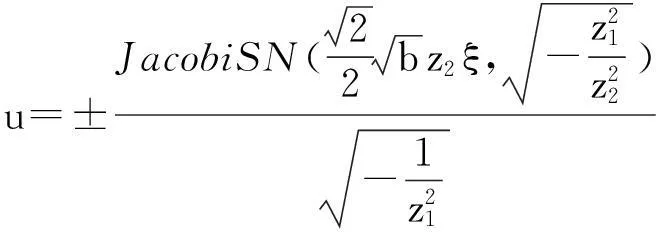
1.5结论

根据以上分析，得到了方程的精确行波解：

(1)当a<0,b<0时

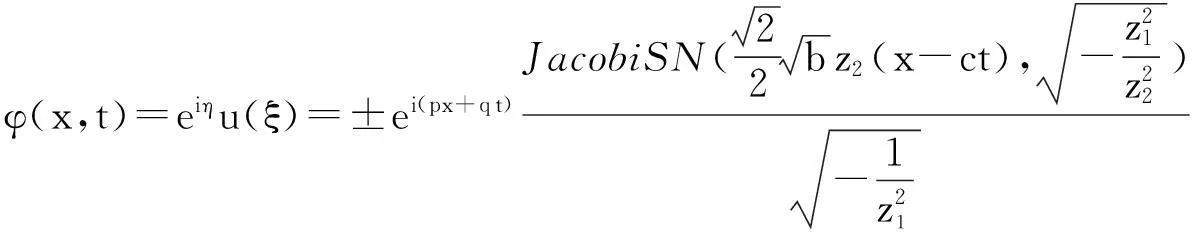
(2)当a>0，b<0时

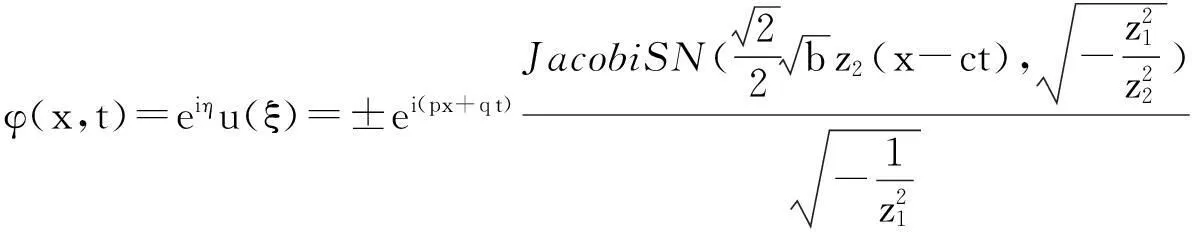
2非线性薛定谔方程的推广形式

近年来，随着对非线性薛定谔方程的研究越来越多，它的推广也变得十分有意义.非线性薛定谔方程的推广形式如下

(4)

2.1非线性薛定谔方程推广形式的行波变换

同样，为了找出此非线性薛定谔方程推广形式的解，设

ψ(x,t)=eiη·u(ξ)

其中，ξ=x-ct，η=px+qt.将u(ξ)简写为u.

根据假设，可以推出

将上式代入(4)式后，两边同时消去eiη，分离实部和虚部后，分别令实部和虚部为零，就得到一个系统

由系统的第一个式子，有uξ=0或1-qc=0.

情况一，当uξ=0成立，解出u=C,其中C是一个常数.

2.2动力系统

由上述系统的第二个方程，得

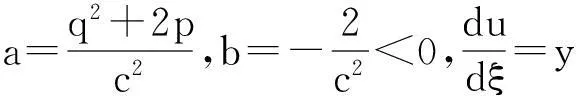
将此动力系统中的两个式子相除，变量分离后积分得到

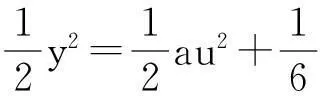
其中，c1是积分常数，通常令c1=0,可得

(5)

由(5)式，得到一个哈密尔顿量

(6)

2.3奇点类型

在奇点A(0,0)时，有λ2-a=0.

(ii)当a<0，b<0时，λ1,2为两虚根，此时A(0,0)为中心(如图4所示).

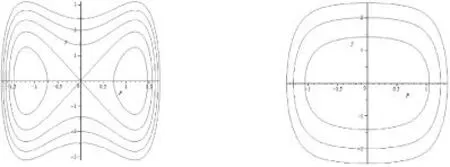
图3　a>0,b<0时奇点的情况　 　　　　　　　　　 图4　a<0，b<0时奇点的情况

Fig.3The situation of singular point when a>0andb<0Fig.4The situation of singular point when a<0andb<0

2.4结果分析

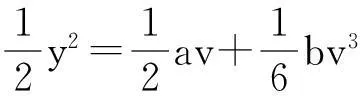
2.5结论

根据以上分析，得到了方程的精确行波解：

(1)当a<0，b<0时

(2)当a>0，b<0时

至此，运用动力系统行波法简单快速求解出了非线性薛定谔方程及其推广形式的精确解，并利用Maple软件画出两个方程解的三维图.与其他方法相比，动力系统行波法求解非线性薛定谔方程方法简单，计算也可以借助Maple软件，而且得到的解更加简洁明了.唯一不足的是，动力系统行波法并不适用于所有的非线性薛定谔方程，必须通过行波法化为哈密尔顿系，否则无法求解.如果对于一些阶数比较高的非线性偏微分方程，因难以求出其奇点，积分问题也难解决.

参考文献:

[1]冯延福，杨慧.一类光学中的非线性Schrödinger方程整体解的存在性[J].云南师范大学学报：自然科学版，2012，32(4)：32-36.

[2]赵强，程秀华，霍叶珂.非线性耦合薛定谔方程组的整体吸引子[J].云南民族大学学报：自然科学版，2014，23(3)：186-189.

[3]ZAKHAROV V E,SHABAT A B.Exact theory of two-dimensional self-focusing and one dimensional sel-modulation of waves in nonlinear medium[J].Sov.Phys.JETP,1972,34:62.

[4]AKHMEDIEV N,SOTO-CRESPO J M,ANKIEWICZ A.Extreme waves that appear from nowhere:On the nature of rogue waves[J].Physics Letters A,2009,373(25):2137-2145.

[5]LI JIBIN.Solitary and periodic traveling wave solutions in Klein-Gordon-Schrödinger equations[J].云南大学学报：自然科学版，2003，25(3)：176-180.

[6]LI JIBIN.Exact explicit traveling wave solutions for (n+1)-dimensional Klein-Gordon-Zakharov equations[J].Chaos,Solitons and Fractals,2007,34(3):867-871.

[7]ZHANG KELEI,TANG SHENGQIANG,WANG ZHAOJUAN.Bifurcation of traveling wave solutions for the generalized Camassa-Holm-KP equations[J].Commun Nonlinear Sci Numer Simulat,2010,15(3):564-572.

[8]GENG YIXIANG,LI JIBIN.Exact solutions to nonlinearly dispersive Schrödinger equation[J].Applied Mathematics and Computation,2008,195:420-439.

Exact Travelling Wave Solutions of the Focusing

Nonlinear Schrödinger Equation

GAO Fang, Ma Rui, XIONG Mei

(College of Statistics and Mathematics,Yunnan University of Finance and Economics,Kunming 650021,China)

Abstract:To solve the nonlinear Schrödinger equation,the former had constructed the rogue wave solutions,but they did not give the exact travelling wave solution of it.In this paper,we chance from the focusing nonlinear Schrödinger equation and its promotion form to dynamical systems by reduce traveling wave system,and discuss the types of the singular points of system after we get the singular points;Then,we divide the system and obtain a Hamilton system.With the help of Maple software,it shows the singular points in the phase portraits clearly;Finally,we take the solutions of dynamical systems back to the focusing nonlinear Schrödinger equation and its promotion form.There are two forms exact traveling wave solutions of NLSE and its promotion form,and it describes the solutions with three-dimensional graph visually.

Keywords:Dynamical systems; Promotion form; Hamiltonian; Singular points; Phase portraits; Traveling wave solutions

中图分类号：O24

文献标志码：A

文章编号：1007-9793(2015)06-0039-06

通信作者：马锐(1963-)，女，云南昆明人，教授，主要从事应用数学方面研究.

作者简介：高芳(1988-)，女，福建平潭人，硕士研究生，主要从事计算数学方面研究.E-mail:386470769@qq.com.

基金项目：云南省教育厅高等学校教学改革研究计划资助项目(2012019).

收稿日期：*2015-09-23