鞍点问题的SSOR半迭代求解方法*
鞍点问题的SSOR半迭代求解方法*
王慧勤,雷刚
(宝鸡文理学院 数学与信息科学学院,陕西 宝鸡 721013)
摘要:针对鞍点问题的特点和SSOR迭代方法的运算优势,给出一种SSOR类型的半迭代求解方法,运用矩阵代数理论分析该迭代方法的收敛性,得到不依赖于矩阵对称正定的收敛条件.最后列举矩阵对称正定及非对称正定条件下的两个数值例子,检验该方法的可行性.
关键词:鞍点问题;迭代法;收敛性
鞍点问题是一种系数矩阵对角块中含有奇异矩阵且对称不定的稀疏线性系统.经常出现在二次优化、电磁学、图像处理、最小二乘问题以及线性弹性力学等科学计算问题中,它们的数值求解最后都归结为对线性系统的求解,这些求解占据了计算量的80%以上,已经成为科学计算中的瓶颈.近年来,不确定的Uzawa方法、预处理的HSS交替方法、SOR-LIKE方法、预处理的Krylov子空间方法等[1-3]已成为求解这类问题的常用迭代方法.
与其他迭代法相比,SSOR半迭代法具有明显的优点.首先,在一些特殊问题中构造的其他迭代法不收敛,但是仍然可以构造出收敛的SSOR半迭代法[4];其次,常见的SOR迭代法、AOR迭代法对参数的选取一般是比较敏感的,而SSOR半迭代法对参数的选择并不敏感[5];第三,SSOR半迭代法能充分利用内外存交换时所得到的信息,减少内外存的交换次数,提高计算效率[6].因此,科学合理的SSOR半迭代方法能够快速求解鞍点问题.
1引言
鞍点问题通常具有如下的形式
(1)
其中矩阵A∈Rm×m是对称正定矩阵,矩阵B∈Rm×n(m≥n)为列满秩矩阵,向量x、f∈Rm,向量y、g∈Rn,向量BT是B的转置矩阵,x、y是未知向量,f、g是已知向量.在实际问题中通常m>>n,此时鞍点问题的解是唯一的[7].
一般地,令
(2)
那么鞍点问题就转化为Wz=b.
通常的做法[1-2]是将W分解为W=D-L-U,其中
引入参数ω,将鞍点问题的系数矩阵分解为如下两种形式
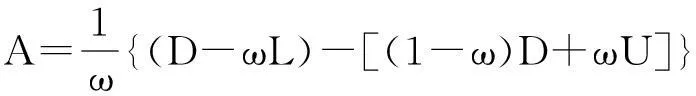
那么建立的SSOR形式的半迭代方法为
(3)
即为
此时生成的SSOR迭代矩阵为
T=(D-ωU)-1[(1-ω)D+ωL](D-ωL)-1[(1-ω)D+ωU]
其中
X11=(1-ω)2I-ω2(1-ω)A-1BQ-1BT-ω2(1-ω)2A-1BQ-1BT
X12=-ω(1-ω)A-1B+ω3A-1BQ-1BTA-1B+ω3(1-ω)A-1BQ-1BTA-1B-ω(1-ω)A-1B
X21=ω+ω(1-ω)Q-1BT
H=[(1-ω)D+ωL](D-ωL)-1ωb+ω(D-ωU)-1b
那么可得半迭代形式下的SSOR迭代算法如下:
设A∈Rm×m是对称正定矩阵,B∈Rm×n(m≥n)为列满秩矩阵,Q∈Rn×n是对称正定矩阵.设定精度ε>0,参数0<ω<2,给定初始向量(x(0),y(0)),k=0,1,2,…,n,….
第二步:计算x(k+1)和y(k+1)
第三步:判断误差,如果

2迭代法的收敛性
引理1[1]设方程组Ax=b,且A为对称正定矩阵,则当0<ω<2时,SOR迭代法和SSOR迭代法是收敛的.
在运用迭代方法求解方程组的过程中,判别迭代法能否收敛的关键条件就是看迭代矩阵的谱半径能否小于1,而矩阵的谱半径又是通过矩阵的特征值来得到的.

引理3如果令μ为矩阵Q-1BTBQ-1的一个特征值,那么当常数λ满足如下等式
[ω(1-ω)+λω]2μ=[(1-ω)2-λ](λ-1)[(1-ω)-ωμ]
时,可以得到常数λ为迭代矩阵T的一个非零的特征值.

(4)
整理可得

由于矩阵A和Q都是对称正定矩阵,并且非奇异,结合(5)可知
[(1-ω)2-λ]A2x=[ω(1-ω)+λω]ABy
求出x的表示式后代入(6)有
[ω(1-ω)+λω]2BTBy=[(1-ω)2-λ](λ-1)[(1-ω)Q2-ωBTB]y
(7)
再利用B∈Rm×n为列满秩矩阵,Q∈Rn×n是对称可逆正定矩阵,令μ为矩阵Q-1BTBQ-1的一个特征值,那么就有
[ω(1-ω)+λ ω]2μ=[(1-ω)2-λ](λ-1)[(1-ω)-ωμ]
(8)
定理1设鞍点问题的系数矩阵中A∈Rm×m是对称正定矩阵,B∈Rm×n(m≥n)为列满秩矩阵,Q∈Rn×n是对称可逆正定矩阵,

(2)当ω=1时,λ=1是矩阵T的一个特征值,对应的特征向量是(1,0,0,…,0)T,SSOR半迭代法不收敛.
证明由引理3可以看出迭代矩阵T的特征值λ满足如下关系
[ω(1-ω)+λω]2μ=[(1-ω)2-λ](λ-1)[(1-ω)-ωμ]
整理可得
λ2[(1-ω)+(ω2-ω)μ]+λ{{2ω2(1-ω)-[ω(1-ω)2+1]}μ
-(1-ω)3-(1-ω)}+(1-ω)3=0
当[(1-ω)+(ω2-ω)μ]≠0时,可得
(1)当0<ω<1时,上述不等式可以转化为
进一步可知
分析上述不等式有
-3ω3+3ω2-ω<0和-3ω3+5ω2-3ω<0

后两个不等式的解为
结合0<ω<1可得到结论.
(2)当ω=1时,由(4)式可得
从上可得,当λ=1时,x=0,此时,λ=1为T的一个特征值,对应的特征向量是(1,0,0,…,0)T.
从式(7)可以看出,SSOR半迭代法的收敛性不依赖于鞍点问题中系数矩阵A的选择,收敛性要求的特征值μ的选取只与系数矩阵中的B和任意选取的矩阵Q有关,这是SSOR半迭代法求解鞍点问题的一个优点.它同时也可以解决鞍点问题中当矩阵A不是对称正定情况下的类鞍点问题.
3数值例子
在数值算例中,由于计算机技术的快速发展,更多配置高、运算速度快的计算机层出不穷,但是为了方便比较,依然将计算机条件设置为较陈旧的T1600,1.66GHz CPU,2.56G RAM Memory,与以往的设置条件完全相同[8-9],选取求解常见的Stokes方程

通常在数值求解过程中首先运用有限元方法进行离散化处理,就可以得到和(1)式相同的方程,这类方程都具有一个重要的特点,那就是系数矩阵的对称性和高度稀疏性,不失一般性假设矩阵A和B分别如下
为了方便计算,向量f和向量g取初始零向量,给定初始向量(x(0),y(0))为单位向量,把预处理需要的矩阵设置为Q=-BTB,那么残量记为

表1 对称正定矩阵下的SSOR半迭代方法的运算结果
从上述的运算结果可以看出,在相同的运算精度的要求下,不同的m和n 取值时,运算所需要的迭代次数和占用CPU的时间不同.与其他已有的迭代方法相比优势也不明显,但是这种半迭代方法能够求解当矩阵A为非对称正定矩阵的情形,像在一些偏微分方程的数值求解过程中[10],系数矩阵只具有高度的系数性,可能并不具备对称性时,这种方法依然可以求解.为同上例比较,取矩阵A和B分别如下
其他向量不变,精度要求也不变,运算结果如下表2.

表2 非对称正定矩阵下的SSOR半迭代方法的运算结果
4总结
依据SSOR迭代方法的特点,把对鞍点问题的求解和SSOR迭代方法结合起来,给出半迭代形式的鞍点问题的求解方法,和其他已有鞍点问题的求解方法相比,在数值运算上看不具有优势,但是它能解决在数值运算中出现的矩阵为非对称时的鞍点问题求解.
参考文献:
[1]潘春平.鞍点问题的预处理HSS-SOR二级分裂迭代方法[J].高校应用数学学报,2009,30(6):905-908.
[2]GUO PENG,LI CUI-XIA,WU SHI-LIANG.A modified SOR-like method for the augmented systems[J].Journal of Computational and Applied Mathematics,2014 (274):58-69.
[3]姜晓林,吕全义,谢公南.一种求解鞍点问题的预处理并行算法[J].应用数学和力学,2014,35(9):1011-1019.
[4]胡家赣.线性代数方程组的迭代解法[M].北京:科学出版社,1991.
[5]邵新慧.大型线性方程组的迭代解法[D].沈阳:东北大学,2006.
[6]韦志辉,周荣富.SSOR数值方法的稳定性[J].东南大学学报:自然科学版,1990,20(3):108-113.
[7]黄卓红.PDE离散方程组和鞍点问题的预处理方法[D].成都:成都电子科技大学,2010.
[8]朱雪芳.求解鞍点问题的一类广义SSOR预条件子[J].数值计算与计算机应用,2014,35(2):117-124.
[9]沈海龙,邵新慧,张铁,等.求解鞍点问题的修正SOR-LIKE方法[J].东北大学学报:自然科学版,2009,30(6):905-908.
[10]张秀梅,王川龙.解鞍点问题的等价模型及其求解[J].工程数学学报,2014,31(1):75-84.
The SSOR Semi-iterative Method for Solving the Saddle Point Problem
WANG Hui-qin, LEI Gang
(College of Mathematics and Information Science,Baoji University of Arts and Sciences,Baoji 721013,China)
Abstract:On the base of the feature of saddle point problems and the operational advantages of the SSOR iterative method,this study make a kind of the SSOR semi-iterative method for solving the saddle point problems.Then analyze convergence of this iterative method using matrix algebra theory,and obtain a convergence condition in non-symmetric positive definite.At last two numerical examples were given for testing application of the method.
Keywords:The saddle point problem; Iteration method; Convergence
中图分类号:O241
文献标志码:A
文章编号:1007-9793(2015)06-0028-06
通信作者:雷刚.
作者简介:王慧勤(1979-),女,陕西榆林人,硕士,讲师,主要从事矩阵计算与数学教育方面研究.
收稿日期:*2015-06-12基金项目:国家自然科学基金资助项目(11371031);陕西省教育厅科学研究计划资助项目(14JK1052);宝鸡文理学院科研基金重点资助项目(ZK15008).

