基于RKDG方法的船体板架爆炸冲击响应数值模拟

于福临， 郭　君， 姚熊亮， 任少飞

(哈尔滨工程大学 船舶工程学院,哈尔滨　150001)



基于RKDG方法的船体板架爆炸冲击响应数值模拟

于福临， 郭君， 姚熊亮， 任少飞

(哈尔滨工程大学 船舶工程学院,哈尔滨150001)

RKDG方法(简称间断伽辽金方法)由Reed等[1]提出，在很长一段时间内仅用于线性方程的求解。Cockburn等[2]结合显式Runge-Kutta方法，利用间断伽辽金法求解了双曲型守恒律方程，间断伽辽金法作为一种新型的计算流体方法开始迅速发展。间断伽辽金方法是介于有限元法和有限体积法之间的一种CFD算法[3]，具备两者的优点。一方面，间断伽辽金法本质上是一种高精度的微分方程空间离散方法，在离散过程中使用弱形式积分，具有有限维解，在单元内使用多项式逼近物理量的真实值，通过简单的增加多项式次数，即可直接提高单元阶数，构造高阶格式，也与有限元方法相似。此外，相比其它可用于流场间断捕捉的空间离散方法，如WENO[4]格式，ENO[5]格式等，间断伽辽金方法不需要大规模的模板，紧凑型极好，求解过程中仅需要当前单元及其直接相邻的单元即可。另一方面，间断伽辽金方法引入数值通量的概念，在单元与单元间计入流场间断，使其可用于冲击波等强间断现象的捕捉，同时还具备多种非线性的限制器，在保证其精度的前提下，抑制非物理振荡，这与有限体积法相似。间断伽辽金法本身就具有高分辨率捕捉的特性，能有效处理水下爆炸中出现的压力、密度、速度等物理量的间断。

本文编制RKDG方法Fortran计算程序，对空中爆炸流场物理特性进行数值模拟，求解冲击波载荷特性，并结合大型非线性有限元软件LS-DYNA，模拟船体加筋板架结构的爆炸冲击响应特征。

1基本方程

1.1流体力学方程组

假设爆轰产物及周围空气为无粘可压缩流，则流体力学方程可用下式表示[4]：

Ut+·F(U)=0

(1)

二维无粘可压缩流的欧拉流体力学方程组如下式所示：

(2)

其中：ρ为流体密度，p为压力，u,v,w为速度，E为单位体积总能量。

1.2Level Set方程

Level Set方程如下：

(3)

(4)

为方便求解将符号函数S(Φ0)光滑化为[6]：

(5)

2RKDG方法

2.1空间离散

由于爆轰流体运动速度相当快，所以可被视为无粘可压缩流。一维无粘可压缩流的DG方法空间离散如图1所示[7]，欧拉方程如下式所示：

U(x,t)t+F(U(x,t))x=0

(6)

将计算区域Ω划分为N个单元，每个单元长度为dxi=dxi+1/2-dxi-1/2。

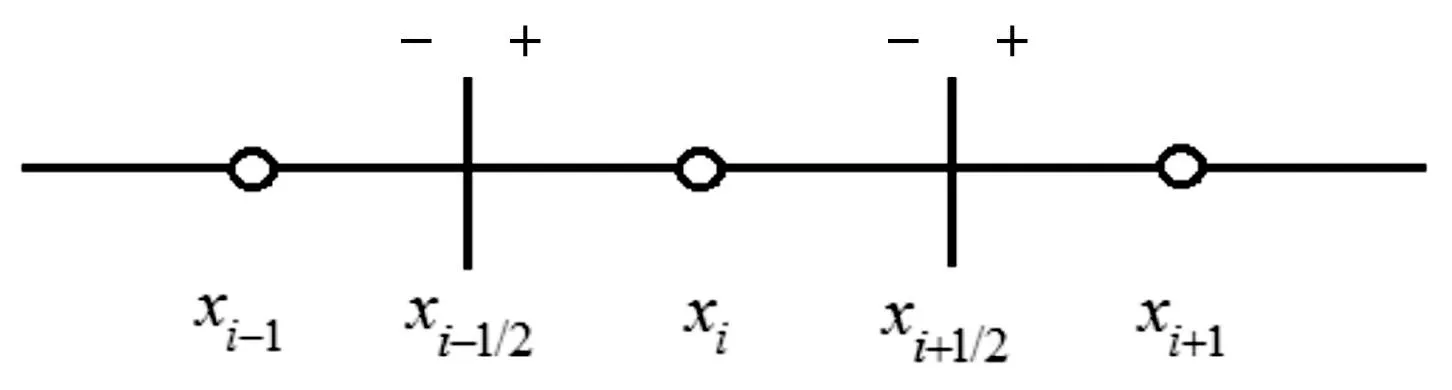
图1　一维DG方法空间离散Fig.1 Discontinuous Galerkin method in 1D spatial discretization

在式(6)两侧同时乘以试探函数w(x)，积分得[8]

(7)

式(7)分部积分得[8]：

(8)

其中：

F(U(xi-1/2,t)t)w(xi-1/2)

(9)

由于边界内侧流体的流通量不连续，可将F(U(xi±1/2,t))进行如下处理[9]：

其中：

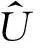
(10)

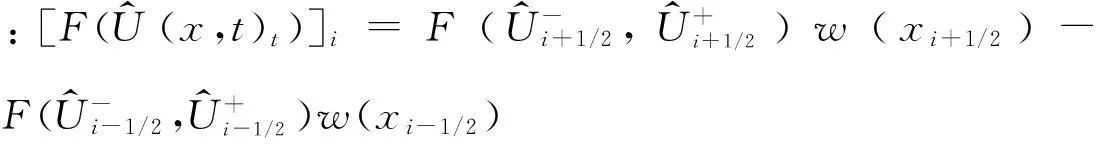
因此式(10)可改写为

(11)

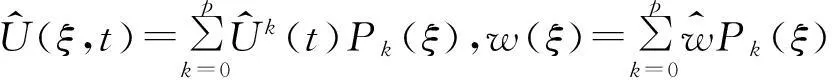
U(t)+Ux(t)P1ξ+Uxx(t)(ξ2-1/3)

(13)

将式(13)代入式(12)中得

(14)

其中:k=0,1,…,p，p为勒让德函数最高阶数，ML求解如下：

(15)

ML=diag[m00m11m22]=

Δxdiag[11/34/45]

(16)

对于多维流体力学方程组采用同样方法，可以得到下式[8]。

(17)

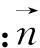
2.2时间离散

采用TVD Runge-Kutta方法对流体力学方程组进行时间离散。设tn时刻流场物理特性为U(0)，则tn+1时刻流场物理特性可由式(18)进行求解[11]：

U(1)=U(0)+ΔtR(U(0))

(18)

其中:R(Uk)可由下式求解[12]:

[Pk(1)F(Uk(1,t))i-

Pk(-1)F(Uk(-1,t))i]}

(19)

Pk为勒让德多项式。

3空中爆炸流场数值模拟

3.1自由场空中爆炸流场载荷数值模拟

采用RKDG方法编制计算程序，模拟自由场空中爆炸流场，并与Henrych经验公式进行对比[13]。表1和图2分别为不同爆距条件下冲击波超压峰值计算值与经验值对比结果。

图2　冲击波超压计算值与经验值对比图Fig.2 The comparison of the peak overpressure of blast wave

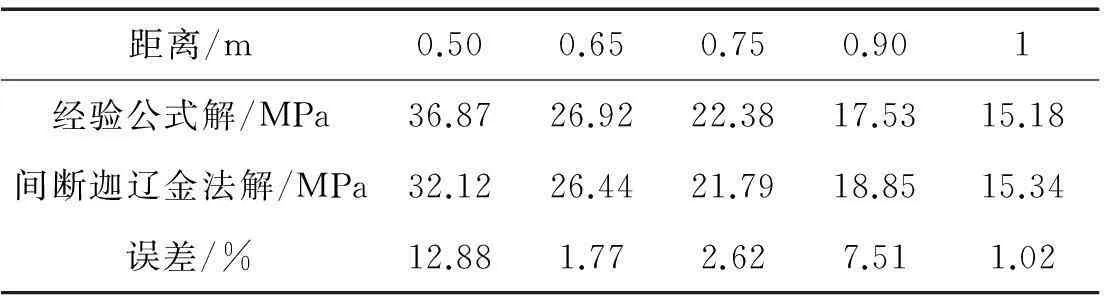
距离/m0.500.650.750.901经验公式解/MPa36.8726.9222.3817.5315.18间断迦辽金法解/MPa32.1226.4421.7918.8515.34误差/%12.881.772.627.511.02

从表1及图2可以看出，RKDG方法计算得到的冲击波超压峰值与经验公式吻合很好，最小误差仅为1.02%，最大误差不超过13%，说明本文提出的RKDG计算程序能够有效模拟空中爆炸冲击波载荷特性。

3.2具有强间断性的空中爆炸流场物理特性

药包为球形TNT装药，空气与爆轰产物采用理想气体状态方程，r=1.4。上下边界设置为固壁边界，左右边界条件设置为流体流出。由RKDG方法计算得到不同时刻整个区域流场的密度、压力分布。

空中爆炸流场密度计算结果如图3所示。

表2　计算工况

图3　不同时刻流场密度分布Fig.3 The density distribution of flow field simulation

空中爆炸流场压力计算结果如图4所示。

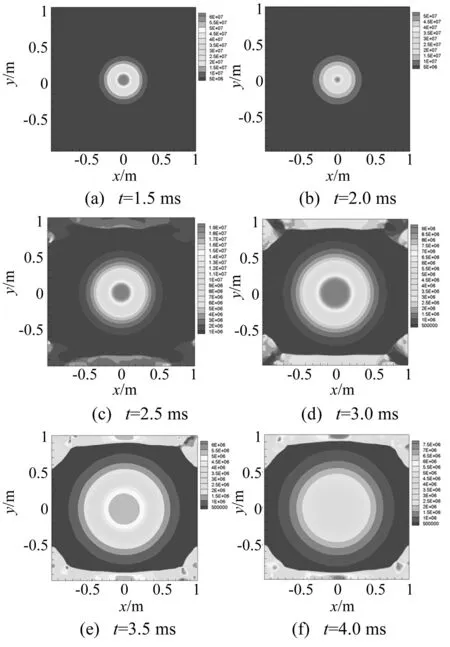
图4　不同时刻流场压力分布Fig.4 The pressure distribution of flow field simulation

由图3可以看出，流场密度随着时间的推移迅速衰减，密度由圆心向四周逐渐减小，当冲击波到达刚性壁面时，壁面密度增大，且边界中心密度大于两侧密度。

由图4可以看出，与密度变化规律相似，冲击波超压随着时间推移迅速衰减，冲击波传播至上下固壁边界时，压力迅速上升，在边界中心形成局部高压，甚至在t=4.0 ms时高于爆心压力。

4空中爆炸船体板架结构响应特性

4.1计算结构模型

图5为船体板架结构有限元计算模型，板架四周刚性固定。

图5　船体板架结构有限元模型示意图Fig.5 The FEM of hull grillage

4.2计算工况和考核点

爆炸流场初始条件如图6所示，上边界为船体加筋板架结构。应用RKDG方法计算整个流场载荷，并与LS-DYNA软件结合，计算船体板架响应特性。

设板架中心的坐标为O(0 m,0 m)，选取四个考核点，坐标依次为A(2.0 m,0 m)、B(1.5 m,0 m)、C(1.0 m,0 m)、D(0.5 m,0 m)。

4.3船体板架毁伤变形

RKDG程序计算时间t=3.0 ms，计算得到冲击波载荷作用大小和范围，结合LS-DYNA软件，计算船体板架结构变形，结果如图7所示。

图6　流场初始条件Fig.6 The initial condition ofair explosion

图7　船体板架毁伤变形Fig.7 The damage deformation of hull grillage

冲击波传播首先达到板架中心，如强间断性空中爆炸冲击波载荷模拟中展示的规律，板架中心处的冲击波压力最大，沿中心向四周压力不断衰减，从图8可以看出，板架中心变形最大，沿板架中心向四周变形逐渐减小，这与冲击波超压分布特性一致，板架结构呈现局部隆起的碟形变形区，且中心处位移最大。这与陈长海、Langdon等[14-15]试验变形结果是一致的。

图8　陈长海、Langdon G S等给出的试验结果[14-15]Fig.8 The test results provided by CHEN Changhai and Langdon G S

时刻/ms1.52.02.5位移/m0.0870.1370.184

4.4船体板架冲击响应

图9为t=0.05 ms时船体板架结构应力响应云图，可以看出，冲击波作用于板架后，T型材区域应力响应明显大于板格应力响应，且在交叉梁处产生了应力集中，应力沿中心向四周逐渐减小。此时最大应力值为5.1×108Pa，在空中爆炸载荷作用下板架沿着T型材出现塑性变形。这与London等[14]观察到的试验结果是一致的。

图10、图11为不同考核点的位移和速度响应曲线。

从图10及表4可以看出，冲击波传播过程中，位移、速度响应随时间逐渐增大，位移及速度响应大小沿板格中心向外逐渐减小，离爆心最近的D点位移、速度响应最大，而A点最小，即板架结构响应与距离爆心距离呈反比。

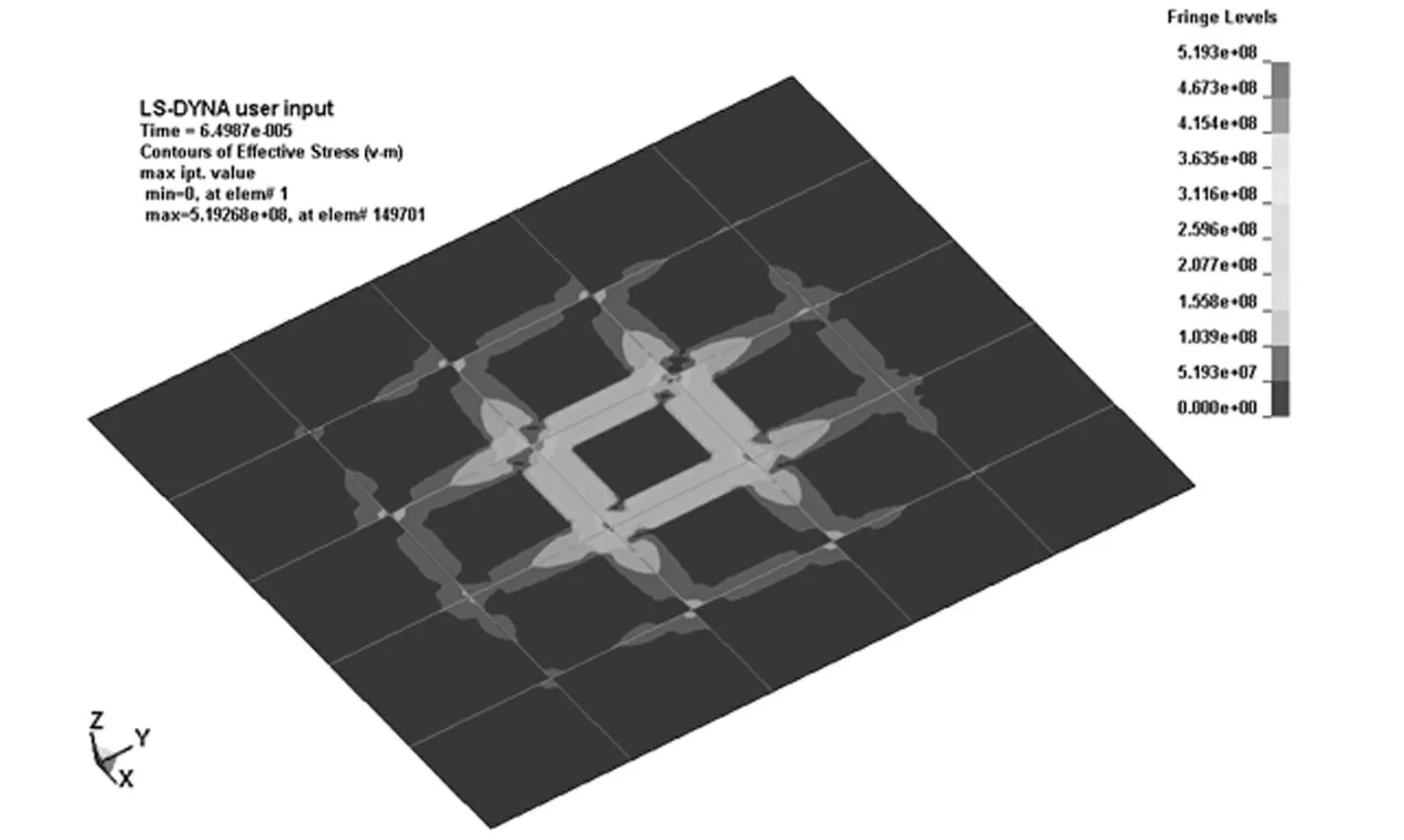
图9　船体加筋板架结构应力响应云图Fig.9 The stress nephogram of hull grillage under far field air explosion

考核点ABCD位移值/cm0.0280.0310.1490.163速度/(m·s-1)16.520.449.8107.6

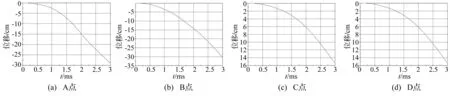
图10　位移响应时历曲线Fig.10 The displacement response time history curve of the inspection point

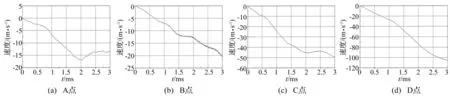
图11　速度响应时历曲线Fig.11 The velocity response time history curve of the inspection point

5结论

本文将RKDG方法应用于空中爆炸流场物理特性求解中，模拟了自由场空中爆炸载荷以及具有强间断性的空中爆炸冲击波流场，给出了流场载荷特性。结合有限元方法，对爆炸载荷作用下典型船体板架结构的响应就行了分析，结论如下：

(1) RKDG方法计算得到的空中爆炸冲击波载荷计算结果与经验公式吻合较好，不同爆距下的超压峰值最小误差为1.02%，最大误差不超过13%，可以有效模拟空中爆炸冲击波载荷特性。

(2) 模拟具有强间断性的空中爆炸流场载荷特性时发现，流场密度随着时间的推移迅速衰减，以爆心为圆心的圆形区域内密度始终最大；而冲击波超压也随着时间推移迅速衰减，冲击波传播至上下固壁边界时，压力迅速上升，在边界中心形成局部高压，甚至在t=4.0 ms时边界中心冲击波超压高于爆心压力。

(3) 分析船体板架结构在空中爆炸载荷作用下的响应特征时，发现板架结构呈现局部隆起的碟形变形，且中心处位移最大，在空中爆炸载荷作用下板架沿着T型材出现塑性变形，与试验结果一致，并发现板架结构响应与距离爆心距离呈反比。

参 考 文 献

[1]Reed W H, Hill T R. Triangular mesh methods for the neutron transport equation [J]. Los Alamos Report LA-UR-73-479, 1973.

[2]Cockburn B, Shu C W. TVB Runge-Kutta local projection discontinuous galerkin finite element method for conservation laws II: General framework[J]. Mathematics of Computation, 1989, 52(186): 411-435.

[3]Jeong W, Seong J. Comparison of effects on technical variances of computational fluid dynamics (CFD) software based on finite element and finite volume methods[J]. International Journal of Mechanical Sciences, 2014, 78: 19-26.

[4]Zhu J, Liu T, Qiu J, et al. RKDG methods with WENO limiters for unsteady cavitating flow[J]. Computers & Fluids, 2012, 57: 52-65.

[5]Susanto A, Ivan L, De Sterck H, et al. High-order central ENO finite-volume scheme for ideal MHD[J]. Journal of Computational Physics, 2013, 250: 141-164.

[6]Osher S, Fedkiw R P. Level set methods: an overview and some recent results[J]. Journal of Computational Physics, 2001, 169(2): 463-502.

[7]Cheng Y, Gamba I M, Majorana A, et al. Discontinuous galerkin solver for Boltzmann-poisson transients[J]. Journal of Computational Electronics, 2008, 7(3): 119-123.

[8]Billet G, Ryan J, Borrel M. A Runge Kutta Discontinuous Galerkin approach to solve reactive flows on conforming hybrid grids: the parabolic and source operators[J]. Computers & Fluids, 2014, 95: 98-115.

[9]Wang Z J. High-order computational fluid dynamics tools for aircraft design[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2014, 372(2022): 20130318..

[10] Du J, Shu C W, Zhang M. A simple weighted essentially non-oscillatory limiter for the correction procedure via reconstruction (CPR) framework[J]. Applied Numerical Mathematics, 2014,279:1-26.

[11] Bo W, Grove J W. A volume of fluid method based ghost fluid method for compressible multi-fluid flows[J]. Computers & Fluids, 2014, 90: 113-122.

[12] Pesch L, van der Vegt J J W. A discontinuous Galerkin finite element discretization of the Euler equations for compressible and incompressible fluids [J].Journal of Computational Physics, 2008, 227: 5426-5446.

[13] Henrych J, Major R. The dynamics of explosion and its use[M]. Amsterdam: Elsevier, 1979.

[14] 陈长海,朱锡,侯海量,等.近距空爆载荷作用下固支方板的变形及破坏模式[J]. 爆炸与冲击, 2008, 32(4): 368-375.

CHEN Chang-hai, ZHU Xi, HOU Hai-liang, et al. Deformation and failure modes of clamped squared plates under close-range air blast loads[J]. Explosion and Shock Waves, 2008, 32(4): 368-375.

第一作者 于福临 男，博士生，1988年生

摘要：基于欧拉流体力学方程组，对方程组分别进行间断迦辽金法空间离散和龙格库塔法时间离散，采用RKDG方法建立数值模型，模拟自由场空中爆炸冲击波载荷特性，并与经验公式对比，对RKDG计算程序进行验证。针对强间断性的空中爆炸冲击波与周围低压空气耦合特性问题，给出了流场密度和压力分布规律。最后编制计算程序，结合大型非线性有限元软件LS-DYNA，模拟板架结构在空中爆炸载荷作用下的变形和响应特征，计算发现：板架沿着T型材出现塑性变形，板格呈现局部隆起的碟形变形区，响应与距离爆心距离成反比。

关键词：间断伽辽金;空中爆炸;耦合特性;数值模拟

Numerical simulation of hull grillage responses under blast loading based on RKDG method

YUFu-lin,GUOJun,YAOXiong-liang,RENShao-fei(College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract:In order to simulate the characteristics of far field air explosion shock load, the discretized Euler equations were solved with RKDG method. The numerical model was established and the far field air explosion shock wave load characteristics were simulated. The results were compared with those of the empirical formula. The density and pressure distribution of high pressure shock wave with strong discontinuity were simulated with a Fortran program. Using LS-DYNA, the impulse responses of hull plates under shock load were simulated. The results indicated that the plastic deformation shape profiles appear along the stiffener direction, and the plate grillages reveal local dishing deformation, and the responses are inversely proportional to the distance from the explosion center.

Key words:discontinuous Galerkin method; air explosion; coupling characteristics; numerical simulation

中图分类号:TH212；TH213.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.13.011

通信作者郭君 男，博士，副教授，1981年生

收稿日期：2014-09-23修改稿收到日期：2015-01-20

基金项目：国家自然科学基金资助项目(51109042)；中国博士后科学基金资助项目(2012M520707)；黑龙江省自然科学基金资助项目(E201124)；黑龙江省博士后资助项目(LBH-Z12064)