弹带挤进过程身管内壁损伤的数值模拟研究

刘广生， 孙河洋， 周　伟

(1.陆军军官学院，合肥　230031 ；2. 军械工程学院，石家庄　050003；3.北京军代局，北京　100042)



弹带挤进过程身管内壁损伤的数值模拟研究

刘广生1,2， 孙河洋2， 周伟3

(1.陆军军官学院，合肥230031 ；2. 军械工程学院，石家庄050003；3.北京军代局，北京100042)

火炮发射过程中，火炮身管内膛材料的损伤、失效及安全性问题一直是学术界和工程界关注的热点和难点[1]。发射过程中身管材料的力学性能主要受两个因素的影响：即挤进过程中弹带与身管内壁的冲击摩擦作用；高温、高压火药燃气对身管内壁的冲刷作用。其中，在弹带与身管内膛的强烈冲击摩擦作用下，位于接触面的某些区域会受到强烈的拉伸作用，如果这种拉伸变形超过材料的拉伸极限，材料就会产生损伤，甚至进一步演化为宏观的裂纹。因为该类问题的研究具有本构关系复杂、计算量特别大等特点，因此国内外对火炮发射过程中内膛损伤进行相关研究的文献几乎没有。

细观损伤力学模型能够从细观层面很好地描述材料宏观的力学性能由于内部损伤累积而逐渐劣化的过程，其中具有代表性的为Gurson模型和GTN模型[2-4]。GTN模型在很多领域得到了广泛的应用，但该模型三个参数的确定存在着很大的争议。Su等[5]分析含有均匀分布空穴的理想刚塑性及考虑应变硬化的理想模型，提出了相应的损伤失稳准则，得到了适合于韧性断裂的计算胞体模型，并通过von Mises准则及相应的失稳准则建立了HLC模型；McVeigh等[6]在Su工作的基础上，将Drucker-Prager准则融入到HLC模型中，得到了适合于描述挤进过程中受压应力状态为主的情况下空穴演化的模型。某型火炮在小规模的实弹射击后发现身管内膛出现横向裂纹，对火炮使用的安全性产生一定的影响。本文在孙河洋等[7-8]提出的弹带挤进模型基础上，采用HLC细观损伤模型对身管内壁进行本构建模，借助显式非线性有限元算法对某型火炮5次发射过程中身管内壁的损伤情况进行了仿真，研究了多发发射情况下弹带挤进过程对身管内壁损伤的影响，从力学角度描述某型火炮身管内壁横向裂纹形成过程。

1有限元模型

以某型火炮的身管、弹丸以及弹带为研究对象，运用有限元前处理软件建立了8节点六面体的有限元实体单元模型，如图1和图2所示。

图1　坡膛有限元模型Fig.1 Finite element model of bore

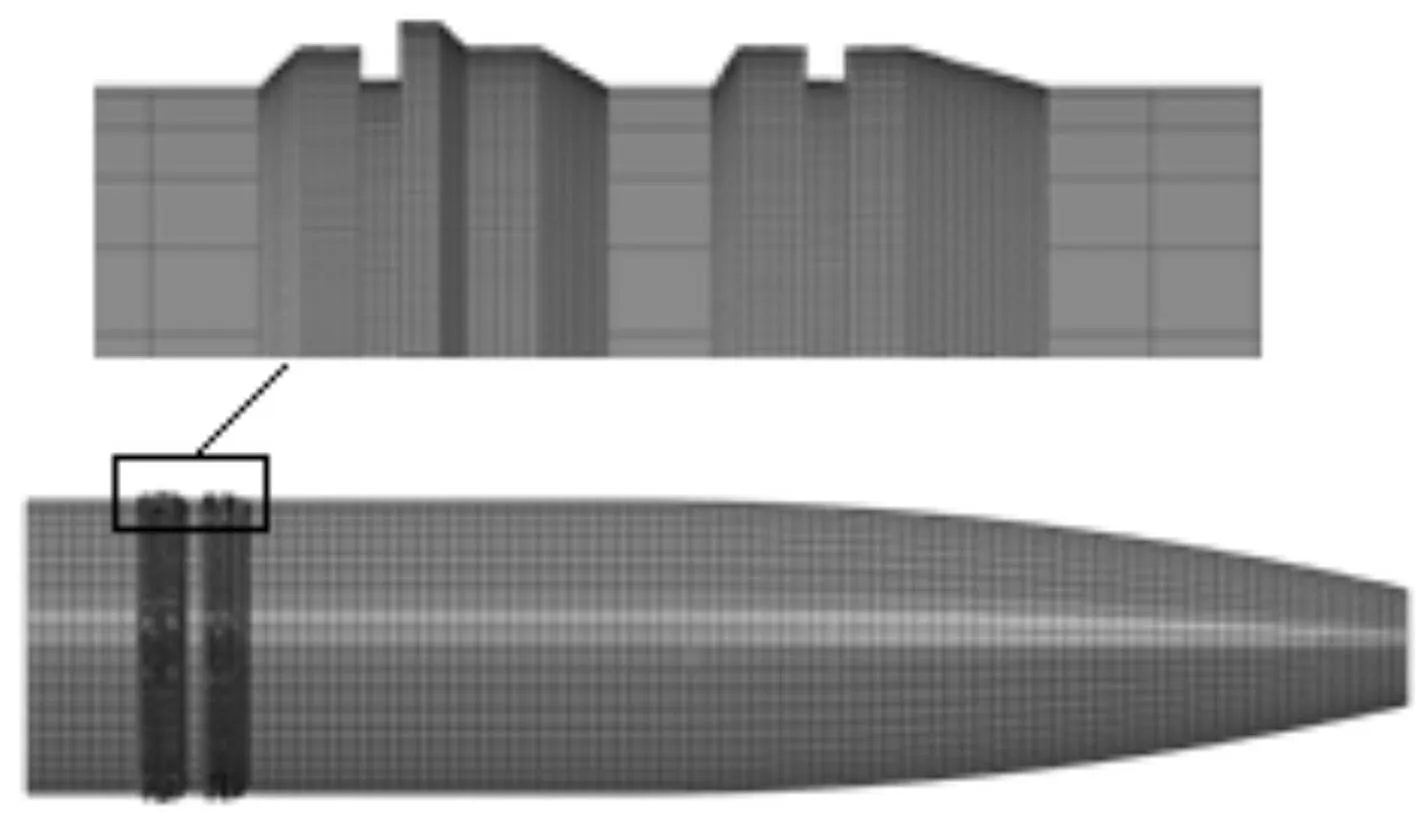
图2　弹带局部放大有限元模型Fig.2 Finite element of band

2本构模型

2.1HLC损伤模型

HLC损伤模型表示如下[6]：

(1)

其中:m20为材料的临界失稳描述，其表达式为

(2)

m1=3k

(3)

对于压力敏感的多孔材料(porous material)多采用Drucker-Prager准则。Cahal McVeigh等在Su工作的基础上，将Drucker-Prager准则引入HLC模型。其中

(4)

可以得到

(5)

其中:α是与空穴体积分数f及应力三轴度σm/σeq无关的模型参数，对于金属α一般取一个微小量，此处取α=0.05[6]。

2.2状态变量的演化[9-10]

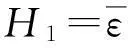
(6)

(7)

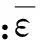
损伤(空穴)的演化包括两个方面：即由原有空穴的增长及新空穴形核引起的损伤的变化。

Δf=Δfgrowth+Δfnucleation

(8)

由于假设基体材料是不可压缩的，因此空穴的增长只与宏观塑性应变的静水分量有关，即

Δfgrowth=(1-f)Δεpl:Ⅰ=

(9)

其中：εpl为宏观塑性应变张量；Ⅰ是二阶单位张量。

本文采用塑性应变控制的形核准则[11]。新孔洞形核造成的孔洞体积分数变化率可由下式表示：

(10)

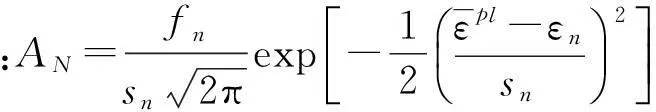
式中：AN为孔洞形核系数；fn为可形核粒子的体积分数大小；εn为孔洞形核时的平均应变；sn为形核应变的标准差。

因此，空穴体积分数总的增量可以描述为

(11)

3本构方程的数值实现方法

本文采用隐式的径向返回应力更新算法[12-13]，通过有限元软件AbaqusExplicit模块的材料子程序接口Vumat[15]，将HLC细观损伤本构模型引入到显式有限元求解计算中。所谓的径向返回应力更新算法包含了弹性预测步和塑性修正步两个部分[9,12]。

3.1率形式本构方程的数值积分[9, 14]

(12)

由等效应力引起的等效塑性应变率定义为

(13)

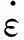
(14)

其中试探弹性应力定义为：

(15)

径向返回应力可以写为两部分：体积增量及偏增量，

(16)

其中:

(17)

为了计算式(17)中的σm,σeq，需要求解Dm,Deq，即对Dm,Deq的相容方程和屈服函数联合进行求解，其方程表述如下

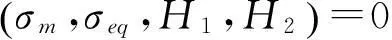
(18)

将式(18)写为适合牛顿迭代求解的形式

(19)

(20)

将两个状态变量对时间微分：

(21)

(22)

两个状态变量对时间的积分可以写为：

Hi,n+1=Hi,n+Δthi,i=1,2

(23)

3.2数值积分实现流程

在本构方程的积分过程中，应力及状态变量需要在每个应变增量步结束时被计算。其具体的实现过程为[17]：

(1) 给定t时刻的初始条件：

(24)

(2) 假定当前时间步的应变增量无塑性出现，计算试探应力：

(25)

这里C为四阶弹性模量。

(3) 计算屈服函数，判断塑性是否产生：

(26)

(4) 塑性修正

用Newton-Raphson方法迭代求解非线性方程组式(19)，进而得到时间步结束时的应力。其流程为：

(a) 将迭代因子设置为k=0

(b) 初始化。假如t=0，则

(27)

否则，采用先前时间步结束步的值。

(d) 更新变量

i=1,2

(28)

σn+1=σe-Δt(KDmI+2GDeqn)

(29)

否则不收敛，k=k+1，转到(c)重新开始计算，反复迭代至收敛为止。

(5) 返回(1)，开始下一时间步长的计算，直到模拟时间结束。

4数值模拟结果及分析

在数值计算过程中，为捕捉到身管内壁单元的损伤失效过程，对身管内壁处的主要接触区域进行网格细化，即和弹带发生接触区域的网格尺寸细化为0.15 mm×0.15 m×0.2 mm。由于网格数量巨大，本文仅对身管内壁的损伤情况进行了5次挤进的数值模拟，每次挤进模拟的物理时间为0.5 ms。为方便模拟结果后处理，取一条膛线，沿其损伤失效处将膛线切开进行后处理结果显示，如图3所示。

图3　裂纹萌生及扩展Fig.3 Crack initialization and growth

图3为进行多发发射模拟得到的火炮身管内壁裂纹萌生的云纹图，图3(a)中显示的即为模拟中裂纹萌生的地方，其位于阳线起点附近，在进行第4次发射模拟时产生。将身管膛线从裂纹处沿身管径向切开，可以看出裂纹萌生于身管的浅表层，类似冲击作用下材料内部孔洞的形成。经过第5次发射初始裂纹开始扩展，如图3 (b)所示。从图中“裂纹扩展”的标识处可以看到损伤的累积仅局限于身管内壁的浅表层，没有向身管外壁进行径向的累积，而主要是自初始裂纹沿身管的周向进行累积，因此裂纹的扩展是沿身管的周向进行的，即形成所谓的“横向”裂纹，这一点在实弹射击实验中得到了验证：该炮经过大约1500发实弹射击后该横向裂纹未沿径向扩展，且逐渐被弹带挤过时磨平。

图4、图5分别为身管模型上所选的6个单元高斯积分点处的基体等效塑性应变曲线图(失效单元的等效塑性应变、屈服应力及损伤值原则上不能减小，图中出现下降趋势的原因是这些单元在第四次计算时失效被删除，第五次计算的结果不存在)。六个单元选取的标准为五次发射模拟时身管模型上损伤最大的单元及发生失效的单元，其单元编号分别为828、41 852、42 380、38 642、42 422及42 436，其中后三个单元为发生失效的单元。从图4可以看出所选单元均发生了较大的塑性形变，其中未失效单元的变形趋势为随着挤进次数的增加其塑性变形越来越小，以单元828和42 380最为明显，这两个单元在前两次挤进时塑性变形较大，后两次挤进时几乎塑性应变没有增加，这体现了身管材料在挤进过程中的硬化现象。

图4 基体材料等效塑性应变Fig.4Effectiveplasticstrainofmatriax图5 基体材料屈服应力Fig.5Yieldstressofmatriax图6 基于HLC模型的损伤值Fig.6DamagevaluebasedonHLCmodel

在整个的挤进过程中有两个因素始终影响着材料单元的性能：材料的硬化及失稳现象。从图5可以看出，与失效单元相比较，未失效单元的基体材料屈服应力在前两次挤进过程中上升的很快，其硬化现象很明显，在后续的挤进过程中硬化现象对材料的影响占主导因素，因此材料在后继的挤进过程中不易屈服，塑性应变相应的较小，因此不易产生损伤。相反，失效单元的塑性形变的趋势是随着挤进次数的增加而呈递增的趋势。塑性应变的增加导致了损伤的累积，因而易产生失效现象。

图6为所选单元的在5次发射模拟中的累积损伤值，即空穴体积分数的值。在数值计算当中材料失稳的临界点为空穴体积分数等于0.15时，从图中可以看出单元42 422及42 436在第三次挤入模拟结束时损伤值已超过失稳临界值，达到了材料的失稳阶段，在第四次挤进模拟时其损伤值迅速上升，直至达到失效阈值直接发生失效被删除。但从总体来看，不论是失效单元或是未失效的单元，其损伤累积的趋势是在材料的临界失稳点之前材料的损伤是随着挤进次数的增加而逐渐减小的，此时材料的硬化占主导因素；在临界失稳点之后，材料的损伤占主导因素，材料损伤累积很快，以致产生最终的失效。

通过5次发射挤进过程的数值模拟可以发现，身管材料的硬化现象和失稳现象始终影响着身管内壁材料的力学性能，致使身管内壁产生的塑性形变不均匀，从而导致裂纹的萌生及扩展。

5结论

本文基于HLC模型对多发发射工况下的身管材料损伤失效问题进行了相关数值模拟研究。数值模拟结果显示身管在4次发射之后产生了位于身管内表面浅表层的细微裂纹，经过第5次挤入模拟后发现该裂纹沿身管周向进行扩展，而未沿径向扩展，即形成了所谓横向发展的裂纹；随着挤入次数的增多，身管最大损伤值的增幅呈下降趋势。靶场实弹射击发现该裂纹未向径向扩展，经过1 500多发射击后裂纹被磨平。因此可以认为数值模拟结果与靶场实验相吻合。本文的数值模拟对火炮身管的安全性设计提供了方向，但是对身管有限元计算结果的应用还需要通过更进一步的相关实验来验证。由于目前实验条件及测试手段的限制，弹带在高温、高压及瞬态的环境下冲击身管内壁的实验研究和验证工作仍有一定难度。

参 考 文 献

[1]张喜发, 卢兴华. 火炮烧蚀内弹道学[M]. 北京：国防工业出版社，2001.

[2]Gurson A L. Continuum theory of ductile rupture by void nucleation and growth: part I—Yield criteria and flow rules for porous ductile media [J]. Journal of Engineering Materials and Technology—Transactions of the ASME, 1977, 99: 2-15.

[3]Tvergaard V. Influence of voids on shear band instabilities under plane strain conditions[J]. International Journal of Fracture, 1981, 17(4):398-407.

[4]Needleman A, Tvergaard V. An analysis of ductile rupture in notched bars[J]. Journal of the Mechanics and Physics of Solids, 1984, 32:461-490.

[5]Hao S, Liu W K, Chang C T. Computer implementation of damage models by finite element and meshfree methods[J]. Comput. Methods Appl. Mech. Engrg, 2000, 187:401-440.

[6]Mcveigh C, Liu W K. Prediction of central bursting during axisymmetric cold extrusion of a metal alloy containing particles[J]. International Journal of Solids and Structures, 2006, 43(10):3087-3105.

[7]孙河洋, 马吉胜, 李伟,等. 坡膛结构变化对弹带挤进过程影响的研究[J]. 振动与冲击, 2011, 30(3)：30-33.

SUN He-yang, MA Ji-sheng, LI Wei, et al.Influence of different bore structures on engraving process on projectile[J]. Journal of Vibration and Shock, 2011, 30(3): 30-33.

[8]孙河洋, 马吉胜, 李伟,等. 坡膛结构变化对火炮内弹道性能影响的研究[J]. 兵工学报, 2012, 33(6):669-675.

SUN He-yang, MA Ji-sheng, LI Wei, et al.Study on influence of bore structure on gun’s interior ballistic performances[J]. Acta Armamentarii,2012, 33(6): 669-675.

[9]Simonsen B C, Li S. Mesh-free simulation of ductile fracture[J]. Int. J. Numer. Meth. Engng, 2004, 60:1425-1450.

[10] Liang X. Constitutive modeling of void shearing effect in ductile fracture of porous materials[J]. Engineering Fracture Mechanics, 2008, 75:3343-3366.

[11] Chu C C, Needleman A. Void nucleation effects in biaxially stretched sheets [J]. Journal of Engineering Materials and Technology-Transactions of the ASME, 1980, 102: 249-256.

[12] Aravas N. On the numerical integration of a class of pressure-dependent plasticity models [J]. International Journal for Numerical Methods in Engineering, 1987, 24: 1395-1416.

[13] Hibbitt, Karlsson, Sorensen. ABAQUS user’s manual version6.6 [M]. Michigan: Hibbitt, Karlsson & Sorensen Inc, 2006.

[14] Vadillo G, Zaera R, Fernández-Sáez J. Consistent integration of the constitutive equations of gurson materials under adiabatic conditions[J]. Comput. Methods Appl. Mech. Engrg, 2008, 197:1280-1295.

[15] Chen Z Y, Dong X H. The GTN damage model based on Hill’48 anisotropic yield criterion and its application in sheet metal forming[J]. Computational Materials Science, 2009, 44:1013-1021.

第一作者 刘广生 男，博士生，讲师，1971年12月生

摘要：针对火炮发射过程中内膛的损伤、裂纹萌生和扩展问题，基于HLC细观损伤本构模型建立了相应的损伤力学有限元数值计算方法，将完全隐式应力更新算法与显式有限元计算相结合，通过用户自定义材料子程序VUMAT将损伤模型嵌入到有限元软件ABAQUS/EXPLICIT模块中。对某型火炮多发射击工况下内膛损伤破坏过程进行了数值模拟计算，分析了弹带挤进内膛过程中身管内壁材料性能随射弹发数变化的规律，并与实验进行了对比。结果表明：HLC细观损伤模型可以有效揭示身管内膛复杂的损伤行为并预测破裂缺陷，为火炮身管安全性设计提供有益的参考。

关键词：细观损伤本构；冲击；身管；VUMAT

Numerical simulation for gun barrel bore damage during shells with into bore

LIUGuang-sheng1,2,SUNHe-yang2,ZHOUWei3(1. Army Officer Academy, Hefei 230031, China; 2. Ordnance Engineering College, Shijiazhuang 050003, China；3. Beijing Military Representative Bureau of General Armament Department, Beijing 100042, China)

Abstract:A damage mechanics finite element numerical computation method was established based on HLC microscopic damage model to solve problems of gun barrel bore damage, crack initialization and growth during gun firing. With this method, the completely implicit stress renewing algorithm was combined with the explicit finite element computation, the damage model was embedded into the finite element software ABAQUS/EXPLICIT module with a VUMAT subroutine. The damage and failure process of the barrel bore of a certain type of gun was simulated numerically during multiple rounds of firings. The law of the barrel bore material performance changing with the number of firing rounds was analyzed during shells with into bore and the simulated results were compared with the experimental ones. The results showed that HLC microscopic damage model can reveal the complicate damage behavior of the barrel bore and predict its cracking defects. The results provided a reference for safety design of gun barrels.

Key words:microscopic damage constitution; impact; nonlinearity; VUMAT

中图分类号:TP391.9

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.13.014

通信作者孙河洋 男，博士，讲师，1984年10月生

收稿日期：2014-04-15修改稿收到日期：2014-07-16