基于分区交错算法的高层建筑风振数值模拟平台及实例

郑德乾，顾 明，张爱社

(1.河南工业大学 土木建筑学院，郑州 450001;2.同济大学 土木工程防灾国家重点实验室，上海 200092;3.山东建筑大学 土木工程学院，济南 250101)

随着建筑高度的增加，以及轻质、高强材料在土木工程领域的应用，结构的风敏感性逐渐增强。在风荷载的作用下，高层建筑结构会发生弯曲或扭转变形;在结构变形的同时，其周围流场也会因为结构外形的改变而变化，风与结构的相互作用问题不是风的流动问题和结构运动问题的简单迭加，二者之间存在着相互耦合的气动弹性现象。以往对于风与结构相互作用问题的研究多采用风洞试验方法［1－3］，随着计算机技术的发展，数值模拟方法逐渐应用于风与结构的相互作用问题求解中［4－11］。

本文讨论的风与结构的相互作用问题，其耦合作用仅发生结构表面上，由两相耦合面上的动力学平衡及运动学协调条件来引入方程上的耦合［4］。直接求解的强耦合法和基于分区交错算法的弱耦合法［4］是数值求解此类流固耦合 (Fluid Structure Interaction，FSI)问题的较常用方法。直接求解的强耦合法将流体域、结构域和耦合作用构造在同一个控制方程中，在同一时间步内同时求解所有变量［4］，这种方法概念清晰，但其分析求解不便于采用现有成熟程序及专业软件。基于分区交错算法的弱耦合法，在每一个时间步内分别依次对CFD(Computational Fluid Dynamics)方程和CSD(Computational Structural Dynamics)方程求解，通过中介交换固体域和流体域的计算结果数据，从而实现耦合求解［4］。在基于分区交错算法的弱耦合法中，CFD和CSD求解过程相互独立，便于采用各领域现有程序及软件实现耦合系统的模块化求解，并且数值模拟结果精度也相对较高，是目前使用相对较广泛的流固耦合问题求解方法［5－11］。

FSI计算中CFD流体域及其边界条件会随时间发生变化，一般可采用达朗贝尔原理［10］或 ALE方法(Arbitrary Lagrangian-Eulerian Method)［11］等手段修改流体域Navier-Stokes(N-S)方程，实现气动弹性问题的求解计算。ALE方法能够较好地解决流体网格的欧拉描述与结构网格的拉格朗日描述的不一致问题，且在考虑网格移动速度的同时能够对运动耦合界面准确描述，已被广泛应用于求解工程领域 FSI问题［5－9］。

本文基于ALE方法和弱耦合分区交错算法，通过对商业流体软件Fluent和结构计算软件Ansys的二次开发，搭建了一个较通用的气动弹性问题数值模拟计算平台。采用该平台，对一宽高比为1∶6的方形截面高层建筑风振气弹响应进行了数值模拟，通过与气弹模型风洞试验及文献模拟结果的对比，以及基于有、无考虑气动弹性时结构位移响应比较的气动阻尼影响分析，验证了本文方法的有效性。

1 数值模拟方法

1.1 控制方程

FSI问题求解中涉及的控制方程主要有CFD流体控制方程、CSD结构运动方程，以及CFDCSD耦合界面相容条件。基于ALE［11］描述的CFD流体域N-S控制方程为:

式中:ρ为流体密度，ν为运动粘性系数，u为流体速度矢量，ug为网格运动速度。在任一运动边界控制体积V上，式(1)的积分形式可写为:

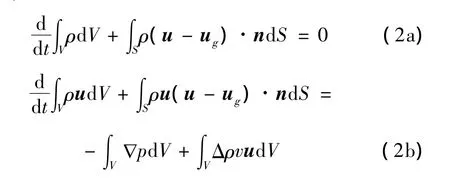
式中:S表示控制体积V的边界，(u－ug)为非定常条件下的对流速度，n为界面法向量。为保证守恒，每个控制体V上应满足网格守恒律:

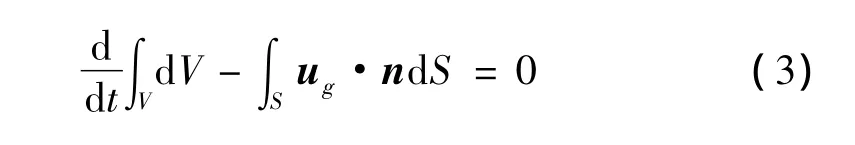
将式(3)对网格速度ug的积分项以通过控制体各面的质量通量(即由控制体各面的运动产生的网格通量)来代替，则式(2)包含网格速度的对流项可被离散为［6，8］:

式中:Φ为广义标量，对于连续方程，Φ=1;对于动量方程，Φ ={u，v，w};c={w，e，s，n，b，t}。经过以上变换，式(2)的求解将基于相对通量(即通过控制体的由流体运动造成的通量减去网格通量)［6，8］，这样即可在网格运动速度ug为未知情况下进行方程(2)的求解。

数值求解FSI问题时，由于CFD和CSD对计算网格要求的不同，导致耦合界面上的网格不匹配［4］，为保证流体－结构耦合系统的一致性，耦合界面的数据传递需要满足力学平衡条件和运动学连续的相容条件，即［6－7］

式(6)为耦合界面力的平衡条件，其中σS是结构应力张量，σF是流体粘性应力张量，p是流体压力。式(7)为耦合界面的位移相容条件，其中uS和 uF分别指耦合界面上结构位移矢量和流体域的位移矢量。

1.2 数值模拟方法

基于弱耦合分区交错算法，本文搭建的高层建筑风振数值模拟平台由四部分组成，分别为:CFD计算模块、CSD计算模块、网格更新模块和数据传递模块。图1a为计算平台构成及各模块的软件实现方法。

(1)CFD计算:基于ALE法［11］的流体控制方程的求解采用有限体积法。基于商业流体软件Fluent，采用Scheme语言编程实现流体计算的参数化、程序化执行。为获得结构表面的平均和脉动风荷载，流体计算采用基于空间平均的大涡模拟 (Large Eddy Simulation，LES)方法。采用动态亚格子模型求解亚格子应力项。LES入流脉动的合成采用文献［12］方法。由于LES方法计算量相对较大，为提高CFD计算效率，流体计算采用并行算法。针对Fluent流体并行计算中流体网格分块和并行计算各进程的特点［13］，采用UDF编程实现流体并行计算时结构表面风荷载的准确提取。本文FSI计算时间步长与CSD计算一致，而CFD大涡模拟时间步长相对较小，为避免时间步长不匹配，CFD计算中采用子迭代技术。

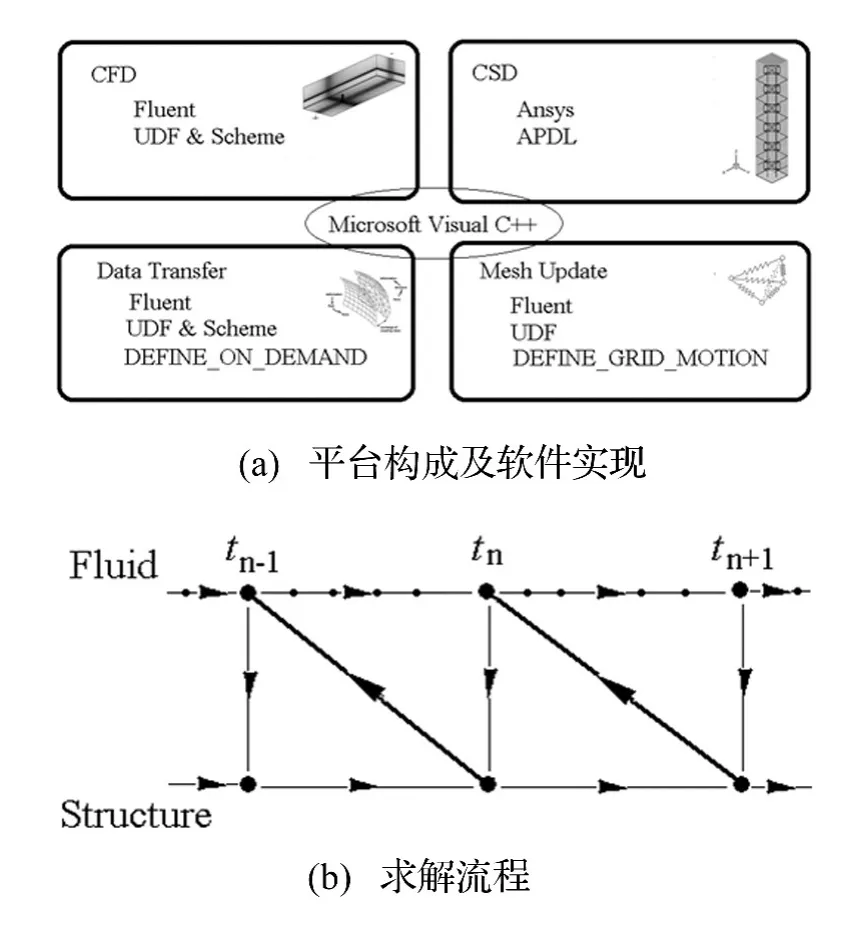
图1 气动弹性数值模拟平台构成、软件实现以及求解流程示意图Fig.1 Sketches of composition and solution procedure of present numerical simulation platform

(2)CSD计算:结构运动方程的求解采用Newmark法［14］。基于结构有限元计算软件 Ansys，通过APDL(Ansys Parametric Design Language)语言实现结构计算的参数化编程。FSI计算的每个时间步，执行CSD计算的Ansys均需要退出，为此采用Ansys重启计算技术来满足结构瞬态响应计算需要。

(3)数据传递:在流固耦合界面上，因CFD和CSD计算对网格密度的要求不同，存在非匹配网格的搜索配对和相应的数据传递问题。本文采用分区搜索算法进行耦合界面网格配对，即对CFD计算中定义的结构各表面分别进行搜索配对，以提高网格匹配效率。基于守恒插值法［7］，采用有限元形函数插值实现流固耦合界面上数据传递，来确保CFD网格传递给CSD网格的荷载平衡，以及CSD网格传递给CFD网格的位移相容。通过UDF编程实现耦合界面非匹配网格的分区搜索配对及数据传递。

(4)网格更新:基于Fluent动网格技术［13］，通过UDF的DEFINE_GRID_MOTION宏编程实现耦合界面的运动变形，采用弹簧光滑法进行流体网格更新。

(5)主进程:基于分区交错算法，采用VC++编制主进程实现上述四个模块之间的调用(图1(a))，本文FSI数值模拟平台求解流程如图1(b)所示。

需要指出的是，当采用本文FSI平台计算时，若每个FSI时间步均不进行CFD模块流场网格的更新，还可实现不考虑气动弹性的结构风致振动数值模拟。

2 算例分析

2.1 计算对象及参数

文献［1］采用一通用超高层建筑结构的多自由度结构模型［2］(如图2所示)，进行了B类1/500缩尺比风场的气弹模型风洞试验，模型的宽度和高度分别为0.1 m 和0.6 m，模型总质量 1.64 kg，实测一阶阻尼比0.0075，实测前二阶基频均为 20.5 Hz。文献［8］基于RANS(Reynolds Averaged Navier-Stockes)方法求解流场，对该模型进行了气弹数值模拟计算。

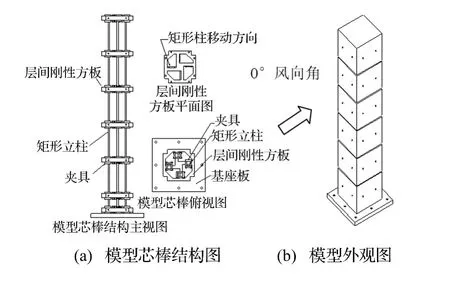
图2 高层建筑结构多自由度气动弹性模型风洞试验结构模型［2］Fig.2 Multi-degree-of-freedom aeroelastic tall building model［2］

采用文献［1］相关参数，基于搭建的FSI数值模拟平台，本文进行了图2所示结构模型0°风向角 (来流垂直于结构迎风面)情况的气弹响应数值模拟。CFD计算采用与风洞试验相同的缩尺比，网格划分如图3(a)所示，图中 B=D=0.1 m，H=0.6 m，网格总数896000，近壁面最小网格尺度为1/2000D，对应壁面y+≤5。CSD建模中分别采用梁单元和壳单元模拟结构的刚度分布和外形，在Ansys中建立了结构的有限元模型，如图3(c)所示。CSD模型两个主轴方向的基频均为20 Hz，非常接近试验模型相应值。耦合界面上的CFDCSD网格分别如图3(b)和图3(c)所示，共计6800个CFD面网格和2500个CSD面网格。

本文FSI计算中，先进行结构静止不动时的CFD大涡模拟计算，待流场充分发展后，释放结构运动，接着进行FSI数值模拟计算。表1为本文FSI计算工况，表中折减风速U*=UH/(f1D)，其中UH为模型高度H处来流平均风速，f1为结构一阶频率。FSI计算中不改变来流风速，通过改变结构固有频率实现不同折减风速变化。表1中所有FSI计算工况的结构质量均为1.64 kg，与文献［1］风洞试验和文献［8］气弹数值模拟保持一致。为分析气动阻尼对结构风振响应的影响，本文还进行了不考虑气动弹性时结构风振响应数值模拟。

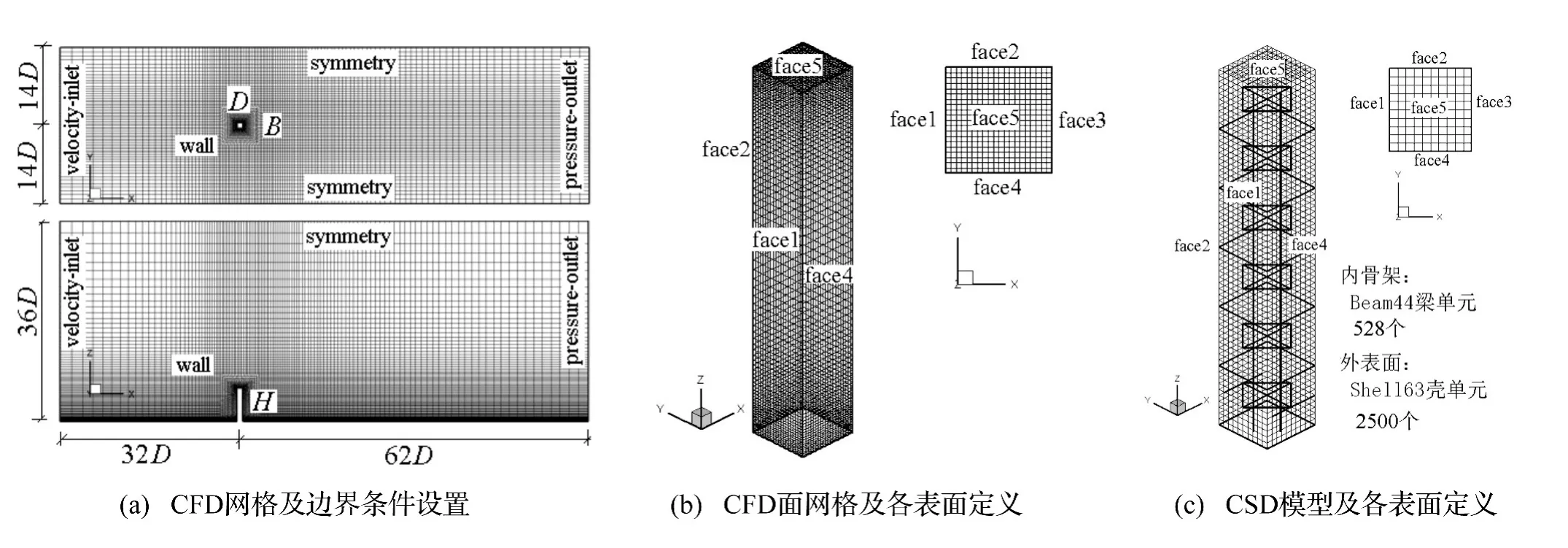
图3 CFD、CSD模型及网格示意图Fig.3 CFD meshes ＆ boundary conditions，and sketches of CSD model

表1 高层建筑风振响应数值模拟工况Tab.1 Case details for study on wind-structure interaction of a tall building

2.2 气弹数值模拟结果比较分析

FSI计算所得高层建筑模型顶部节点位移响应根方差与文献［1］气弹模型风洞试验和文献［8］数值模拟结果的比较如图4所示。由图可见:① 本文数值模拟所得结构的顺风向响应与模型风洞试验结果总体上吻合较好，只是数值模拟结果数值偏小;② 对于结构的橫风向响应，本文气弹数值模拟结果与风洞试验结果也具有较好的一致性，并且精度明显高于基于RANS的气弹数值模拟结果。

2.3 有、无考虑气动弹性数值模拟结果比较分析

数值模拟所得有、无考虑气动弹性时，不同折减风速下结构顶部节点位移响应时程的比较如图5所示，图6为位移响应根方差随折减风速的变化比较。由图可见:① 折减风速较小时，有、无考虑气动弹性时结构顺风向位移响应振幅及根方差比较接近，不考虑气动弹性结果稍大;随着折减风速U*的增加，结构顺风向位移响应振幅均有所增大，不考虑气动弹性情况的振幅增大相对显著，由图6(a)可明显看出两种情况下位移响应根方差数值上的差异随U*的增加逐渐增大。② 折减风速U*＜12.0时，有、无考虑气动弹性时结构横风向位移响应的比较结果与顺风向类似;但折减风速增大至U*=12.0，横风向涡激共振发生时，结构横风向气弹位移响应振幅及其根方差值明显大于不考虑气动弹性结果，此时气动阻尼对结构风振响应的影响不可忽略。

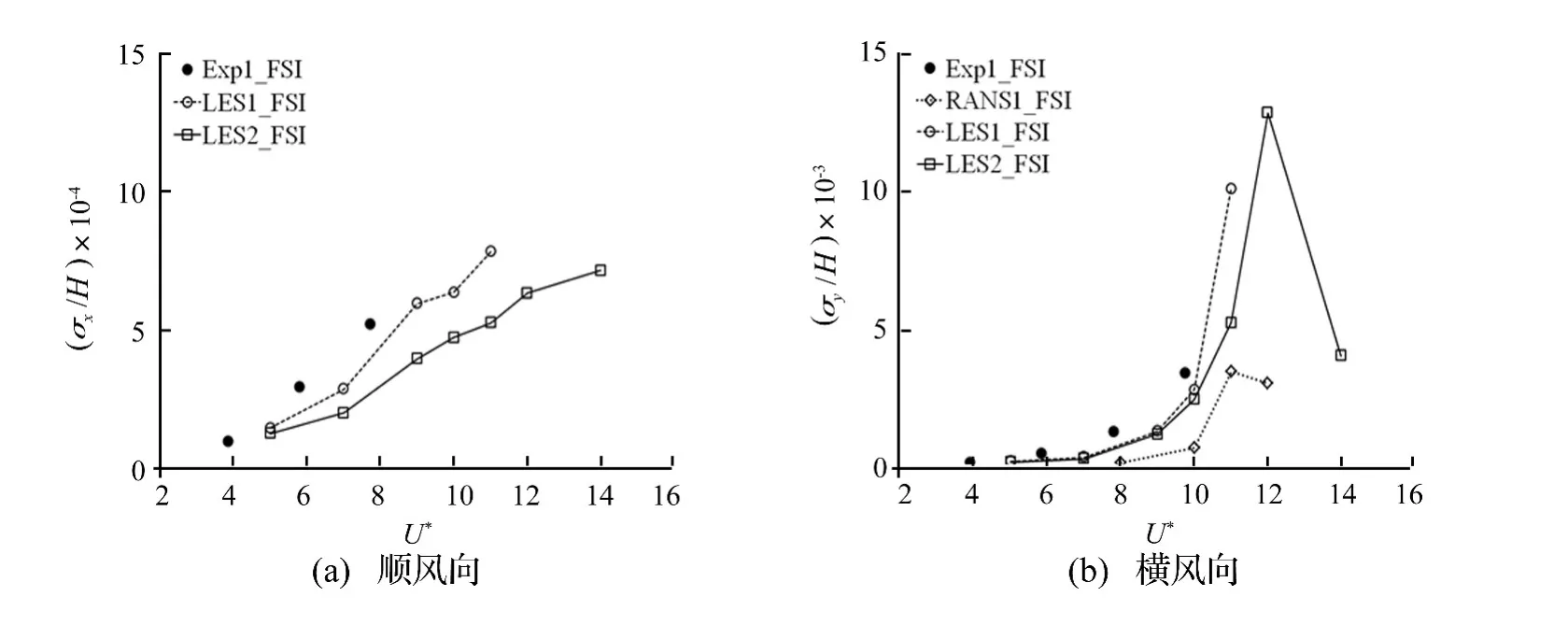
图4 模型顶部节点气弹位移响应根方差的比较Fig.4 Comparison results of r.m.s values of aeroelastic displacement responses of points at the top of the building model

图5 有、无考虑气动弹性时模型顶部节点位移响应时程数值模拟结果比较Fig.5 Comparisons of time histories of displacement responses of points at the top of the building model between present simulation results with and without considering FSI

图6 有、无考虑气动弹性时模型顶部节点位移响应根方差数值模拟结果比较Fig.6 Comparisons of displacement responses of points at the top of the building model between present simulation results with and without considering FSI

由以上分析结果可推断:本文计算折减风速范围内，顺风向气动阻尼均为正值;而横风向气动阻尼则随着折减风速的增加，由正值逐渐变为负值。这与文献［15－16］的试验研究结果基本一致。

3 结论

基于弱耦合分区交错算法，通过对商业流体软件Fluent和结构计算软件Ansys进行二次开发，搭建了风与结构相互作用气动弹性问题数值模拟计算平台。采用本文方法，对三维方形截面高层建筑风振响应进行了数值模拟分析。结果表明，基于本文方法的气弹数值模拟结果与试验结果基本一致，并且精度上高于已有文献数值模拟结果;有、无考虑气动弹性时结构风振响应数值模拟结果的比较表明，折减风速较小时，气动阻尼的存在有利于减弱结构的顺、横风向风振响应;但当折减风速增大至出现横风向涡激共振现象时，气动阻尼的存在明显增强了结构的横风向振动。本文方法可以较精确地数值求解高层建筑结构的风振气弹响应问题。

［1］黄鹏.高层建筑风致干扰效应研究［D］.上海:同济大学，2001.

［2］全涌，顾明.超高层建筑通用气动弹性模型设计［J］.同济大学学报，2001，29(1):122－126.QUAN Yong，GU Ming.Design of super-high rise buildings’global aeroelastic model［J］.Journal of Tongji University，2001，29(1):122－126.

［3］章李刚，楼文娟.复杂外形超高层建筑结构三维风致响应分析［J］.振动与冲击，2013，32(24):38 －43.ZHANG Li-gang，LOU Wen-juan.Three dimensional windinduced responses of super-tall buildings with irregular geometric shapes［J］.Journal of Vibration and Shock，2013，32(24):38－43.

［4］钱若军，董石麟，袁行飞.流固耦合理论研究进展［J］.空间结构，2008，14(1):3－15.QIAN Ruo-jun，DONG Shi-lin，YUAN Xing-fei.Advances in research on fluid-structure interaction theory［J］.Spatial Structures，2008，14(1):3－15.

［5］Braun A L，Awruch A M.Aerodynamic and aeroelastic analyses on the CAARC standard tall building model using numerical simulation［J］.Computers ＆ Structures，2009，87(9－10):564－581.

［6］Glück M.Computation of wind-induced vibrations of flexible shells and membranous structures［J］.Journal of Fluids and Structures，2003，17(5):739 －765.

［7］Farhat C，LeTallec M L P.Load and motion transfer algorithms for fluid/structure interaction problems with nonmatching discrete interfaces:Momentum and energy conservation，optimal discretization and application to aeroelasticity［J］.Comput.Methods Appl.Mech.Engrg.，1998，157:95 －114.

［8］方平治.典型建筑结构气动弹性问题的数值模拟研究［D］.上海:同济大学，2007.

［9］Michalski A，Kermel P D，Haug E，et al.Validation of the computational fluid-structure interaction simulation at realscale tests of a flexible 29m umbrella in natural wind flow［J］. Journal of Wind Engineering and Industrial Aerodynamics，2011，99(4):400 －413.

［10］Tutar M，Holdo A E.Large eddy simulation of a smooth circular cylinder oscillating normal to a uniform flow ［J］.Journal of Fluids Engineering，2000，122:694－702.

［11］Hirt C W，Amsden A A，Cook J L.An arbitrary Lagrangian-Eulerian computing method for all flow speeds［J］.Journal of Computational Physics，1997，135:203－216.

［12］Zheng D Q，Zhang A S，Gu M.Improvement of inflow boundary condition in Large Eddy Simulation of flow around a tall building［J］.Engineering Applications of Computational Fluid Mechanics，2012，6(4):646－660.

［13］Fluent.Inc.Fluent 6 Documentation，2005.

［14］Bathe K J.Finite element procedures［D］.Prentice-Hall，Englewood Cliffs，1996.

［15］Gu M，Quan Y.Across-wind loads of typical tall buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，2004，92(13):1147 －1165.

［16］Quan Y，Gu M，Tamura Y.Experimental evaluation of aerodynamic damping of square super high-rise buildings［J］.Wind and Structures，2005，8(5):309 －324.