宽带直扩信号的随机解调压缩采样方法*



宽带直扩信号的随机解调压缩采样方法*

程艳合**,杨文革,韩丙寅

(解放军装备学院 光电装备系,北京 101416)

摘要：为了有效解决扩频测控通信系统宽带化带来的高速采样压力和高数据率问题,提出了基于压缩感知的直扩信号随机解调压缩采样方法。通过对模拟信号压缩采样原理进行研究,深入分析和推导随机解调采样原理及其数学模型,提出了基于压缩感知的直扩信号采集系统构架,并对压缩比取值影响因素进行了分析；给出了随机解调压缩采样系统硬件实现方案,并对其可行性进行了分析；最后对所提出的直扩信号压缩采样方法的性能进行了仿真分析。仿真结果表明,压缩采样系统可以实现直扩信号的压缩采样处理,并能够高精度重构原信号,但重构信号的解调门限会随压缩比增大而相应提高,这是采样率降低所需付出的代价。压缩采样为宽带直扩测控通信系统提供了一种高效的模数转换和同步解调处理思路。

关键词：扩频测控通信；宽带直扩信号；压缩感知；压缩采样；随机解调

1引言

在航天测控通信领域,为了应对日益激烈的空间信息对抗形势,并获得更高测距精度,扩频体制系统的扩频带宽进一步增大,给接收机前端A/D变换提出了很高要求,致使接收机按照Nyqiust采样定律进行采样变得非常困难。另一方面,即使测控系统能够以Nyqiust速率进行采样,带宽增加意味着数据率提高,系统将面临高数据率问题,给后续传输、记录存储和同步解调处理带来沉重负担[1]。因此,有必要研究一种能够降低采样速率的方法。

压缩感知(Compressive Sensing,CS)理论作为一种新型的信息获取理论,一经提出就成为了数学及工程应用领域研究热点,目前已取得很多研究成果,特别是针对Nyquist采样数据的后续数字信号处理,已进行了很多比较成功的应用尝试[2]。然而,CS理论的主要创新是可将模拟信号直接转换到信息域,在降低采样频率的同时实现信息的有效采集,压缩采样就是这种创新优势的集中体现[3]。压缩采样是压缩感知应用领域由数字向模拟的扩展,与传统Nyquist采样或带通采样相比,压缩采样方法可以直接把模拟信号投影到变换域,有效降低信号采样频率,充分体现了压缩感知理论优势,为缓解扩频信号高速采样、高速数据传输存储提供了一个崭新的思路。

近来,针对扩频信号的压缩感知研究越来越受关注。文献[4]通过构造稀疏基字典对直扩测控通信信号进行稀疏性分析,初步探讨了该类型信号压缩感知相关问题。文献[5]针对扩频通信信号,提出了一种基于压缩感知的信号采集和恢复方法,并仿真验证了其可行性,但未考虑模拟信号压缩采样及其实现问题。目前,国内外关于模拟信号压缩采样研究对象主要集中在频域稀疏的单子带、多子带连续波信号[6]以及脉冲雷达信号[7]等相关领域,针对直扩信号压缩采样的系统性研究未见报道。

压缩感知理论框架主要包括稀疏基字典、测量矩阵、重构算法三部分内容[2],其中文献[4]已经构造了直扩信号稀疏基字典,信号重构算法可以采用常见的正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[8]。本文主要针对模拟直扩信号压缩采样问题展开全面研究：首先给出基于CS的直扩信号采集系统结构,对模拟信号压缩采样基本原理进行研究,分析和推导随机解调采样原理及其数学模型,并研究压缩比取值的影响因素；然后提出随机解调采样系统硬件实现方案,并对其可行性进行分析；最后仿真分析基于随机解调压缩采样的直扩信号接收系统性能。

2基于压缩采样信号接收系统框架

基于CS理论框架,首先给出基于压缩采样的直扩信号接收系统结构框架,如图1所示。

图1　基于压缩采样的直扩信号接收系统

本系统主要包括模拟信号压缩采样和压缩域信号处理两部分。其中,压缩采样模块主要进行接收信号压缩采样处理,实现直扩信号模数转换,最终获得压缩状态数字信号,这也正是本文的研究重点。

3直扩信号压缩采样模型研究

3.1模拟信号压缩采样原理

从数学角度出发,离散信号压缩感知的线性测量过程y=Φx实际上就是测量矩阵Φ行向量分别与离散信号x[n]做内积运算,如图2(a)所示。以此类推,对于模拟信号x(t)压缩采样,需要将离散域压缩感知扩展至连续域,寻求能够在硬件平台上实现的压缩感知,在模拟域同时实现信号采样和压缩处理,如图2(b)所示。具体而言,需要将测量矩阵Φ扩展为连续形式,可以通过连续内积实现上述转变,而且内积处理可以由积分器来实现。目前,模拟域压缩感知已经有了初步研究,其中随机调制压缩采样由于其硬件实现简单、效果较佳得到了广泛关注[9]。

(a)离散信号压缩降维

(b)模拟信号压缩采样

3.2随机解调压缩采样理论分析

3.2.1随机解调采样基本原理

随机解调采样主要由伪随机码生成器、乘法器、积分器与低速ADC四部分组成,包括随机解调、积分和低速采样三个处理过程,如图3所示[9]。

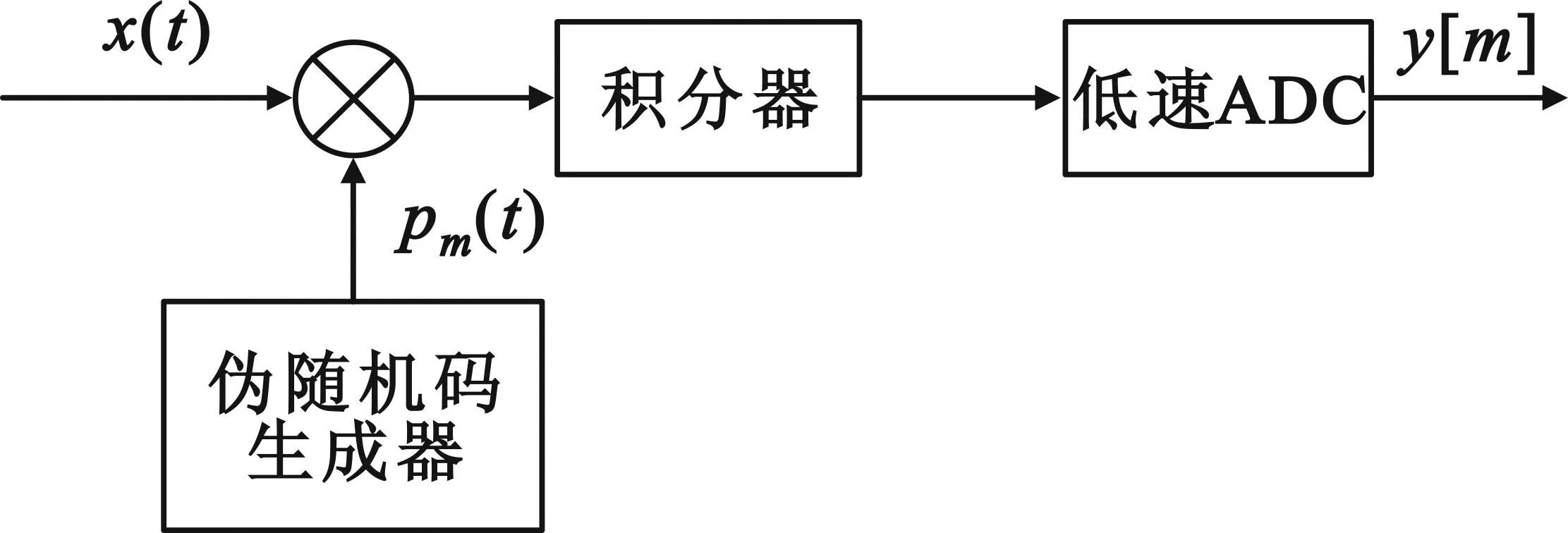
图3　随机解调采样结构框图

(1)

输入模拟信号在随机解调处理之后,其信息已经遍布整个频带,可以对结果进行低通滤波来获取信号信息,此处由积分器来等效代替低通滤波器,但需要保证积分时间与后续低速采样时间间隔相同,其输出可表示为

(2)

式中,Ts表示积分时间,τ是积分变量。

针对积分器输出结果,直接采用传统ADC进行低速的均匀采样,最终获得输入信号的压缩采样值,这些采样值无损地涵盖了输入信号的全部信息,其数学表达式为

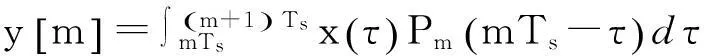
(3)

3.2.2随机解调采样数学模型

在数学上,压缩采样系统可以等效为一个测量矩阵,可以把输入信号x(t)的Nyquist采样值x[n]映射为离散测量序列y[m],如图4所示。测量矩阵对于压缩采样信号重构或压缩域直接信息提取等后续的相关处理而言必不可少,因此本节对随机解调采样所对应的测量矩阵进行推导。

图4　压缩采样等效原理

假设所有数据处理都是在有限长窗口N内进行,则有输入信号Nyquist采样值是长度为N的一维向量,相应的压缩测量值为长度为M(≤N)的一维向量。图5给出了随机解调压缩采样的等效离散数学模型。

图5　随机调制采样离散数学模型

则式(3)可转变为

(4)

y=HDx。

(5)

式中,x是以Nyquist频率离散化的输入信号；y是压缩采样输出信号；D∈RN×N是用于随机解调的伪随机码Pm[·]所对应的矩阵,具体为

(6)

H∈RM×N是积分清零器对应的累加降采样矩阵,具体形式如下:

(7)

综上分析可得,随机调制采样系统对应测量矩阵Φ=HD,大小为M×N,并且N=M×L,其中L表示Nyquist采样率与压缩采样率之比,称为压缩比。

3.2.3等效测量矩阵RIP特性分析

在压缩感知理论框架中,测量矩阵和稀疏基字典的乘积(即感知矩阵)要满足受限等距(RestrictedIsometryProperty,RIP)条件,但要证明感知矩阵是否满足等距受限特性,过程非常复杂,为此Bareaniuk提出了一个等价条件：测量矩阵和稀疏基字典不相关[2]。本节通过相关性分析来检验该压缩采样等效测量矩阵的RIP特性。首先给出测量矩阵Φ和稀疏变换基Ψ之间的相关系数定义:

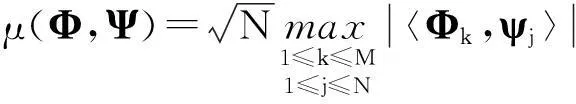
(8)

图6给出了等效测量矩阵与稀疏字典相关系数的变化规律,在实验中直接序列扩频(DirectSequenceSpreadSpectrum,DSSS)信号稀疏基字典采用延时-多普勒字典,基字典维数N=5600,压缩比L变化范围为[1,800],每种压缩比仿真次数为100。

图6　相关系数变化规律

3.3压缩比取值范围分析

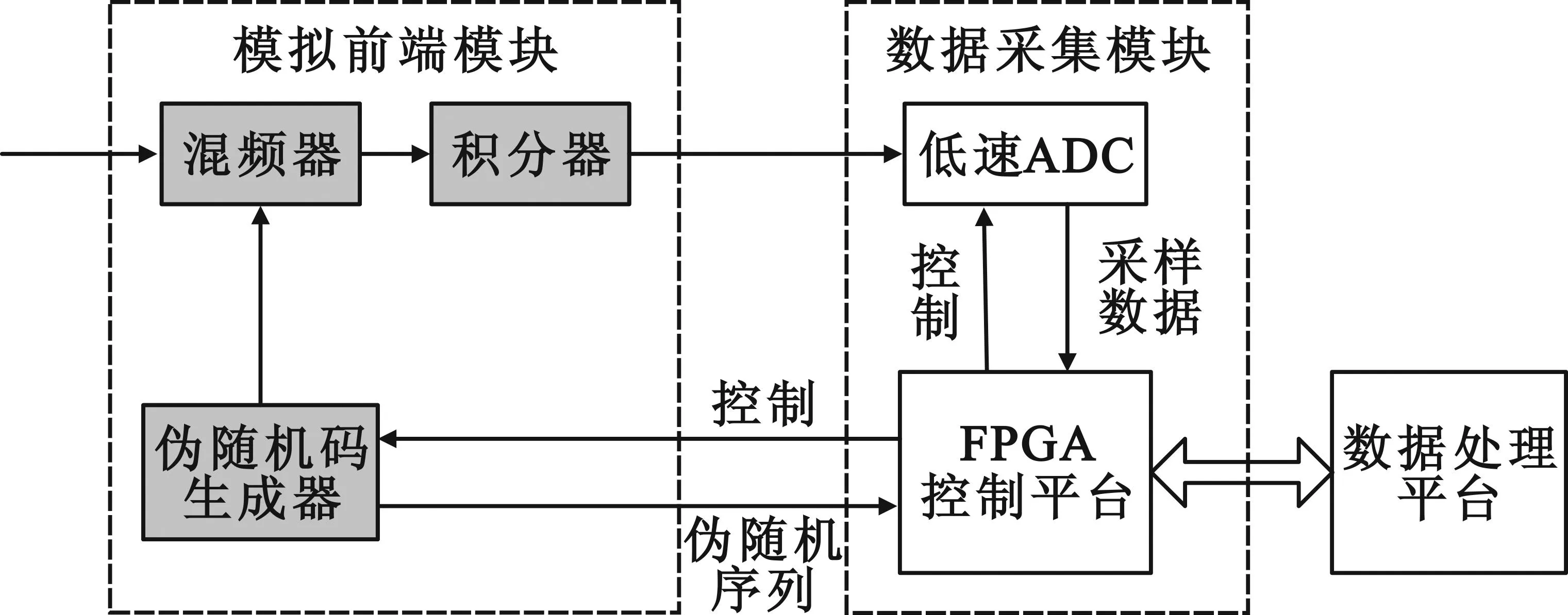
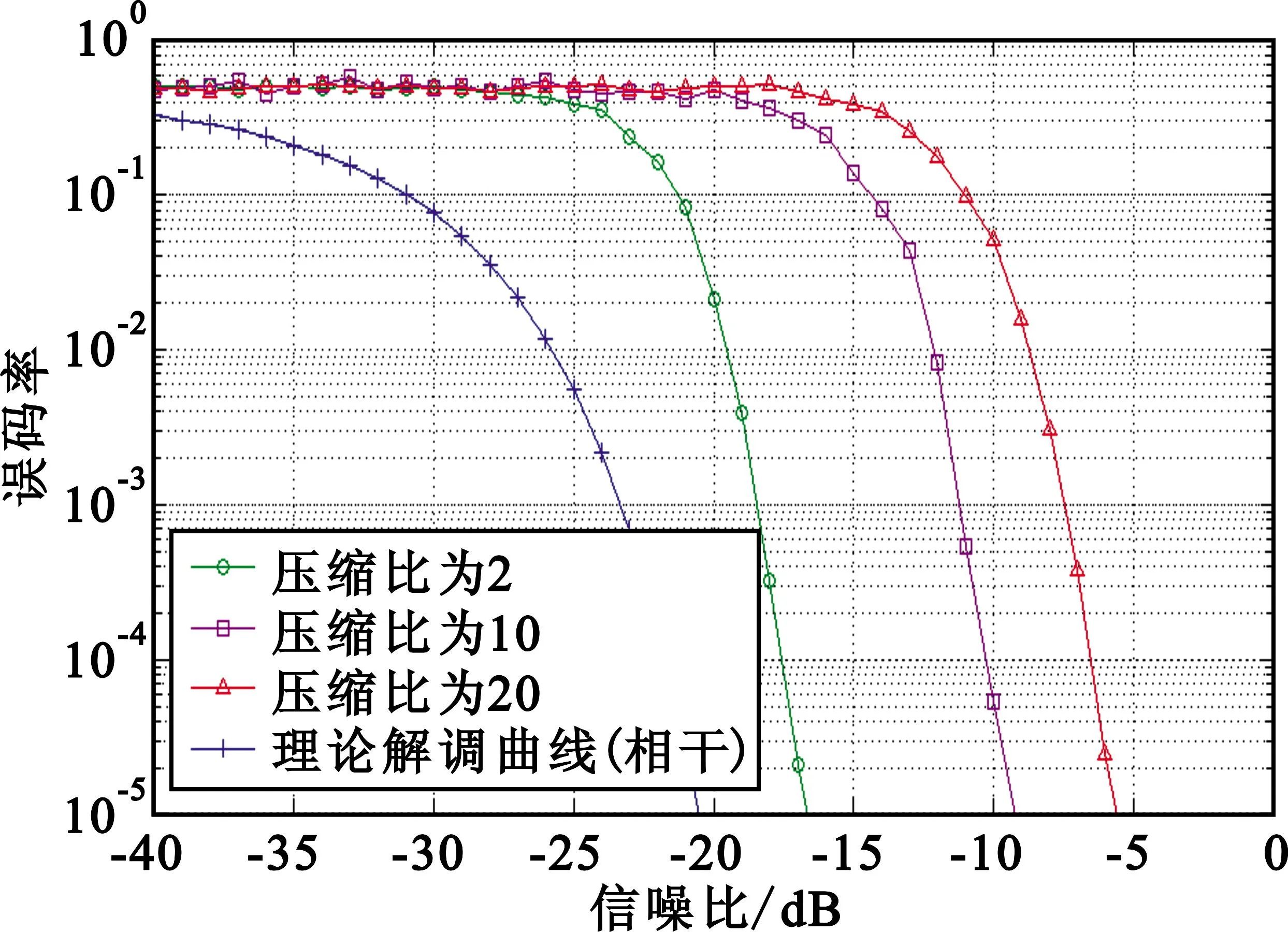
压缩测量实质上是一个投影的过程,也就是将具有稀疏性的长度为N原始信号直接投影到一组测量基(即测量矩阵)上,得到M(M<

根据压缩感知理论可知[2],如果要高概率满足压缩感知理论的先验条件,即RIP特性,压缩测量必须满足关系式

(9)

M≥C×K×lg(N/K+1)。

(10)

式中,K是信号稀疏度,C是常数因子,N与M分别是压缩前后的信号维度。结合压缩比定义,由式(10)可以得到压缩比取值范围为

(11)

由式(11)可以得出如下压缩比取值规律：

(1)压缩比取值上界与分段处理信号长度成正比,随信号长度增大而提高；

(2)压缩比取值上界与常数因子成反比,随C的增大而降低,这表明在相同情况下,要想获得更高压缩比,更大地降低采样率,需要系统等效测量矩阵与准备采集信号稀疏基字典相关性要足够低；

(3)压缩比取值上界与分段处理信号的稀疏度成反比,即信号稀疏度越低,压缩比的取值可以越高,获取原信号所包含全部信息的所需压缩采样值个数也就越少。

4硬件实现方案与可行性分析

直扩信号随机解调压缩采样系统的最大优势就是由硬件实现较为简单的宽带模拟域混频技术替代硬件实现较为困难的高速AD采样技术,由模拟域混频带宽和伪随机序列转换速率共同决定系统输入带宽,解决了ADC输入带宽限制难题,可以有效降低宽带直扩信号采样系统硬件实现复杂度。

4.1硬件实现方案设计

图7所示为采样系统实现框架,主要包括模拟前端与数据采集模块两部分,其中前者包含混频器、伪随机码生成器和积分器,后者包含低速ADC和FPGA等器件。

图7　直扩信号压缩采样硬件框图

首先,模拟信号与伪随机码发生器生成的高速随机序列之间进行混频,同时把对应的伪随机码存储在FPGA中,以备用于采样值后续的信号重构或压缩域信息提取等相关处理；混频输出信号经过积分器,滤除高频分量；FPGA控制积分器积分间隔和低速AD采样间隔,完成积分器结果的低速AD采样,最终实现模拟信号的压缩采样处理过程,并将采样值传输给后续的数据处理平台。

4.2可行性分析

直扩信号随机解调压缩采样系统主要由伪随机码生成、乘法运算、低通滤波、低速ADC四部分组成,其中与传统Nyquist采样相比,低速ADC没有特殊要求,硬件实现不存在困难,但伪随机码生成、相乘和积分运算都工作在高速环境下,必须保证它们在高速工作时的精确度,设计要求比较苛刻。

(1)高速伪随机序列产生可由最大长度线性反馈寄存器实现。目前,移位寄存器的软硬件实现已经发展比较成熟,生成序列符号改变速率可达到80Gb/s[10]；

(2)伪随机序列与输入信号的高速相乘运算可由混频器实现。当运行在高速状态时,一般常见混频器输出是非线性的,但无源混频器具有良好的线性度和噪声性能,且工作频率可以达到5GHz[11]；

(3)由积分器来实现压缩采样中低通滤波功能,更具体地说,可采用差分输入输出有源RC滤波器,由于其放大增益有限存在一个特定时间常数,可作为由时间常数确定截止频率的低通滤波器。

5仿真实验及结果分析

本节对直扩信号随机解调压缩采样方法进行仿真实验验证。为了简化仿真实验复杂度,实验参数参考当前现役主流系统指标设置。为了定量描述,首先定义压缩采样信号重构相对误差如下：

(12)

在仿真实验中,直扩信号稀疏表示采用文献[6]构造的延时-多普勒基字典,信号重构采用OMP算法[10],数据率Rb为10kb/s,伪码周期1023,码速率Rc为10MHz,中频fc为70MHz,采样率fs=56MHz,传输延时量化精度Δτ=Ts,多普勒频率量化精度Δfd为1Hz,延时适用范围[0,1/Rb],多普勒适用范围[-1000,1000]Hz,其中误码率统计的数据位数取1×107。

5.1仿真实验

实验一:首先不考虑噪声,仿真分析压缩采样系统欠采样能力。针对不同的压缩比多次重复实验,统计每种压缩采样率下的重构相对误差和解调误码率情况,其中每种情况统计的误码个数不能低于100,以保证误码率的可靠性。在实验中,压缩比变化范围取L=[1,800],结果如图8和图9所示。

图8　相对误差随压缩比变化图

由图8可知,在低压缩比时,信号重构相对误差较小,基本保持在10-6以内,可以认为高精度地重构了原信号；当压缩比高于200时,相对误差逐渐增大；在高压缩比(大于400)时,相对误差保持在较大的水平。

图9　解调误码率与压缩比关系图

由图9可知,在低压缩比时,压缩采样值的重构信号解调误码率保持为零,即随机解调采样能够获取原信号的全部信息；当压缩比大于200后,解调误码率逐渐增大,这与理论分析保持一致,此时压缩采样点数已经达到理论门限。

实验二：固定压缩比,仿真分析压缩采样在更贴近实际信号环境下,即含有加性高斯白噪声,系统性能的变化规律。在实验中,信噪比变化范围取[-30dB,30dB],其他参数与实验一相同,结果如图10和图11所示。

图10　相对误差随信噪比变化图

由图10可知,在压缩比取10情况下,当低信噪比时,信号重构相对误差较大,保持在1以上；相对误差随信噪比增大而快速降低；当信噪比高于-5dB时,相对误差都可以保持在0.1以内。

图11　解调误码率与信噪比关系图

根据图11可以发现,压缩采样值的重构信号解调误码率随着信噪比改善而降低；重构信号的解调误码率门限随压缩比增大而提高,压缩比取2、10和20三种情况时,信噪比要分别达到-17dB、-9dB和-6dB时,误码率才能达到10-5量级；与理论相干解调曲线相比,三种压缩比的解调误码率门限(对应10-5)分别近似恶化了4dB、12dB和15dB,这是采样率分别降低了2、10和20倍所付出的代价。

5.2实验结果分析

通过以上的仿真实验,可以得出以下结论：

(1)随机解调采样模型能够实现直扩信号的压缩采样,且结合延时-多普勒基字典,能够准确重构出原信号,并实现正确的解调处理,证明了基于随机解调采样的直扩信号接收系统的可行性；

(2)随机解调压缩采样重构信号的解调门限随压缩比增大会相应提高,这是采样率降低所需付出的代价。

值得注意的是,为了简化仿真实验复杂度,仿真参数采用的是当前主流系统20MHz带宽直扩信号,压缩欠采样意义看似不大。根据理论分析已知,对不同带宽的输入信号,压缩采样模型适用性相同。因此,当直扩信号带宽升高到百兆赫甚至上千兆赫以后,即使压缩采样率只比Nyquist采样率降低2倍,压缩采样系统的收益也会非常明显。

6结束语

本文针对直扩信号压缩采样问题进行了系统性研究,基于对模拟信号压缩采样和随机解调采样模型的深入分析,提出了直扩信号随机解调压缩采样系统框架,并给出了其硬件实现方案。仿真分析表明,本文所提方法能够实现直扩信号的压缩采样及其重构解调处理,但重构信号的解调门限会随压缩比增大而提高。因此,压缩比不能太高,要综合考虑信号稀疏性、系统带宽、信道环境等相关因素,在系统容限以内慎重取值。压缩采样为宽带直扩测控通信系统提供了一种高效的模数转换和同步解调处理思路。后续的研究工作将进一步构建压缩采样硬件试验平台,并深入研究基于CS的直扩信号同步解调处理。

参考文献：

[1]刘嘉兴. 飞行器测控与信息传输技术[M]. 北京: 国防工业出版社,2011.

LIUJiaxing.SpacecraftTT&CandInformationTransmissionTechnology[M].Beijing:NationalDefenseIndustryPress,2011.(inChinese)

[2]KazunoriH,MasaakiN,ToshiyukiT.Auser′sguidetocompressedsensingforcommunicationssystems[J].IEICETransactionsonCommunications,2013,96(3):685-712.

[3]CandèsEJ,WakinMB.Anintroductiontocompressivesampling[J].IEEESignalProcessingMagazine,2008,25(2): 21-30.

[4]程艳合,杨文革，张令军. 采用压缩感知的直扩测控信号处理[J]. 电讯技术,2015,55(2): 129-134.

CHENGYanhe,YANGWenge,ZHANGLingjun.DSTT&Csignalprocessingbasedoncompressivesensing[J].TelecommunicationEngineering,2015,55(2): 129-134.(inChinese)

[5]安建平,王帅,王铁星,等. 基于压缩感知的直接序列扩频信号采集和恢复方法：中国,102710568[P]. 2012-10-03.

ANJianping,WANGShuai,WANGTexing,etal.Directsequencespreadspectrumsignalacquisitionandrecoverymethodbasedoncompressivesensing:China,102710568[P].2012-10-03.(inChinese)

[6]AngrisaniL,BonavolontaF,D′ApuzzoM.Acompressivesamplingbasedmethodforpowermeasurementofband-passsignals[C]//Proceedingsof2013InternationalConferenceonInstrumentationandMeasurementTechnology.Minneapolis:IEEE,2013:102-107.

[7]BudillonA,EvangelistaA,SchirinziG.Three-DimensionalSARfocusingfrommultipasssignalsusingcompressivesampling[J].IEEETransactionsonGeoscienceandRemoteSensing,2011,49(1): 488-499.

[8]WangJ,KwonS,ShimB.Generalizedorthogonalmatchingpursuit[J].IEEETransactionsonSignalProcessing,2012,60(12): 6202-6216.

[9]SmailiS,MassoudY.Accurateandefficientmodelingofrandomdemodulationbasedcompressivesensingsystemswithageneralfilter[C]//Proceedingsof2014InternationalSymposiumonCircuitsandSystems.Melbourne:IEEE,2014: 2519-2522.

[10]DicksonTO,LaskinE,KhalidI,etal.An80-Gb/s231-1pseudorandombinarysequencegeneratorinSiGeBiCMOStechnology[J].IEEEJournalofSolid-StateCircuits,2005,40(12): 2735-2745.

[11]HsiaoYC,MengCC,SyuJS,etal. 5-6GHz9.4mWCMOSdirect-conversionpassive-mixerreceiverwithlow-flicker-noisecorner[C]//Proceedingsofthe7thEuropeanMicrowaveIntegratedCircuitsConference.Amsterdam:IEEE,2012: 301-304.

程艳合(1987-),男,河北衡水人,博士研究生,主要研究方向为航天测控技术、扩频信号处理、压缩感知理论；

CHENGYanhewasborninHengshui,HebeiProvince,in1987.HeiscurrentlyworkingtowardthePh.D.degree.HisresearchconcernsaerospaceTT&Ctechnology,spreadspectrumsignalprocessingandcompressivesensing.

Email:cheng20130810@foxmail.com

杨文革(1966-),男,江西金溪人,教授、博士生导师,主要研究方向为飞行器测控与通信系统、压缩感知理论；

YANGWengewasborninJinxi,JiangxiProvince,in1966.HeisnowaprofessorandalsothePh.D.supervisor.HisresearchinterestsincludespacecraftTT&Candcommunicationsystemandcompressivesensing.

韩丙寅(1986-),男,辽宁沈阳人,博士研究生,主要研究方向为航天测控技术、扩频信号处理、高性能计算。

HANBingyinwasborninShenyang,LiaoningProvince,in1986.HeiscurrentlyworkingtowardthePh.D.degree.HisresearchconcernsaerospaceTT&Ctechnology,spreadspectrumsignalprocessingandhighperformancecomputing.

引用格式：程艳合,杨文革,韩丙寅.宽带直扩信号的随机解调压缩采样方法[J].电讯技术,2015,55(5):472-478.[CHENG Yanhe,YANG Wenge,HAN Bingyin.Compressive Sampling of Broadband DS Signal Based on Random Demodulation[J].Telecommunication Engineering,2015,55(5):472-478.]

Compressive Sampling of Broadband DS Signal

Based on Random Demodulation

CHENG Yanhe,YANG Wenge,HAN Bingyin

(Department of Optical and Electronic Equipment,The Academy of Equipment,Beijing 101416,China)

Abstract：In view of the high-speed sampling and high data rate pressures which come from broadband of the direct sequence spread spectrum tracking,telemetry and command(DS TT&C) system,a DS signal compressive sampling method based on compressive sensing(CS) is provided. Firstly,the DS signal acquisition system architecture based on CS is proposed. Then,the random demodulation sampling principle and model are analyzed according to analog signal compressive sampling theory,and influence factors of compressive ratio are investigated. Finally,a hardware design for DS signal compressive sampler based on random demodulation is provided,and the feasibility of proposed architecture is explored. The results show that the proposed system can realize the compressive sampling of DS signal,and the original signal can be reconstructed accurately. Moreover,the demodulation threshold of reconstructed signal will increase with compressive ratio,which is the required price for deducing sampling rate. The technology provides a novel analog digital conversion and synchronous demodulation method for DS TT&C system.

Key words：DS TT&C;broadband DSSS signal；compressive sensing;compressive sampling；random demodulation

作者简介：

中图分类号：TN911.7

文献标志码：A

文章编号：1001-893X(2015)05-0472-07

通讯作者：**cheng20130810@foxmail.comCorresponding author：cheng20130810@foxmail.com

收稿日期：*2015-02-12；修回日期：2015-04-07Received date:2015-02-12；Revised date：2015-04-07

doi:10.3969/j.issn.1001-893x.2015.05.002