新型复合GIL/GIB温升模型仿真计算
吴趣鸿,董立辉,朱 勇,曹冬林,仲留寄
(江苏神马电力股份有限公司,江苏南通226553)
新型复合GIL/GIB温升模型仿真计算
吴趣鸿,董立辉,朱勇,曹冬林,仲留寄
(江苏神马电力股份有限公司,江苏南通226553)
摘要:气体绝缘复合管道输电线路(简称复合GIL/GIB)是一种新型输电技术,其复合壳体是在金属材料内衬层表面缠绕一定厚度的质量轻、成本低、耐腐蚀性强的复合材料层而形成的。针对新型复合GIL/GIB的温升问题,建立了其温升模型,将电磁场、流体场、温度场进行耦合仿真求解。考虑了温升模型的热平衡状态以及相关材料物性参数的温度效应,将仿真结果与实际温升试验测量结果比较,总结得出了相关的结论,从而为复合GIL/GIB的设计、制造及工程应用提供一定的理论依据。
关键词:复合GIL/GIB;温升;趋肤效应;自然对流
中图分类号:TM751
文献标识码:A
DOI:10.3969/j.issn.1672-0792.2015.06.010
收稿日期:2015-04-05。
作者简介:吴趣鸿(1987-),男,助理工程师,主要从事高压GIL设计研发工作,E-mail:wuquhonggodric@163.com。
Abstract:Composite gas-insulated transmission line/gas-insulated transmission busbar (for short, composite GIL/GIB) is a new technology of power transmission. Its composite enclosure is made of metal material lining layer and a certain thickness of light-weight, low-cost, strong corrosion-resistance composite material layer wound on the surface of the material lining layer. In order to solve the problem of the temperature rise resulting from the new composite GIL/GIB, this essay has established the temperature rise model which couples the electromagnetic field, fluid field and temperature field. Considering the thermal equilibrium state of the temperature rise model and the temperature effects of the physical parameters of related materials, this essay compares and contrasts the simulation results and the actual temperature rise test measurements. It concludes that they provide some certain theoretical basis for the design, manufacture and engineering application of composite GIL/GIB.
Keywords:composite gas-insulated transmission line/gas-insulated transmission busbar; temperature rise; skin effect; natural convection

0引言
气体绝缘复合管道输电线路(复合GIL/GIB)作为一种新型的高电压、大电流电力传输设备,相较于传统金属GIL/GIB,其复合壳体是在金属材料内衬层表面缠绕一定厚度的质量轻、成本低、耐腐蚀性强的复合材料层而形成的。复合壳体的金属层厚度约为传统金属壳体厚度的一半,同时复合壳体的设计相较传统金属壳体更适合直埋式安装,因此复合GIL/GIB具有更好的经济性优势。
复合GIL/GIB同样面临温升发热的问题。温升不仅限制了复合GIL/GIB的最大载流能力,而且过高的温升会直接影响其内部非导电材料的绝缘性能,从而降低使用寿命,影响供电可靠性[1~3]。复合GIL/GIB的金属层更薄,壳体环流产生的电阻热损耗更大;同时,复合壳体表面的复合材料导热系数远小于金属的导热系数,不利于内部热量向外传递。因此,研究复合GIL/GIB的温升问题对于复合GIL/GIB的设计、制造及工程应用都有着重要的意义。
本文的温升模型是建立在电压等级252 kV、电流等级4 000 A的复合GIL/GIB试验样机的基础上,试验环境为常规大气环境,该试验样机已经通过西安高压电器研究所型式试验验证。
本文利用有限元多物理场仿真[4~7]软件,仿真求解复合GIL/GIB温升模型,将仿真结果与型式试验中的温升试验结果进行比较,最后得出一些合理的结论,从而为复合GIL/GIB的设计、制造及工程应用提供一定的理论依据。
1仿真模型求解域的建立
考虑到复合GIL/GIB三维温升模型仿真求解的计算量极大,因此将三维模型进行适当简化。假设复合GIL/GIB水平敷设,同时假设其水平方向无限长,因此可以选取垂直于长度方向的同轴圆柱截面作为研究对象,建立二维仿真模型求解域示意图如图1所示[8-9]。二维模型求解域由铝导体、铝壳体、玻璃钢壳体、内部SF6气体、外部空气等区域以及相应的边界组成。B1,B2,B3,B4为固体和气体接触边界,B5为空气远场开边界。

图1 二维仿真模型求解域示意图
2电磁场模型及边界条件
建立电磁场模型的目的是为了仿真求解出铝导体和铝壳体单位长度的电阻热损耗,并将其作为流体场、温度场模型仿真求解的热源。铝导体和铝壳体的电导率是随温度变化的参数,所以必须考虑电导率的温度效应。因此电阻热损耗也是随着温度的变化而变化的瞬态变化量。二维模型求解域中的铝导体和铝壳体区域可以看成两个封闭的单匝线圈,在垂直于线圈截面的方向上加载固定频率(50 Hz)的正弦线圈激励电流。当在铝导体上通入一定大小的电流时,铝壳体会产生几乎同样大小的反向感应电流(壳体环流)[10]。通入的线圈激励电流大小是根据GIL/GIB运行时的额定电流Ir以及其温升试验标准要求来确定的[11]。电磁场模型的仿真求解主要依据安培定律,同时设定空气远场开边界B5为磁绝缘边界。
3流体场、温度场模型及边界条件
3.1 热源及热量传递方式
在不考虑外界热辐射的情况下,温度场模型的热源主要由两部分组成,分别是铝导体和铝壳体单位长度的电阻热损耗,其值可由电磁场模型求解得到。热量总是由高温物体向低温物体方向传递,形成明显的温度梯度分布趋势。温度场模型中涉及到热传导、热辐射和热对流3种基本传热方式[12]。复合壳体内部主要通过热辐射和封闭空间自然对流这两种方式将热量传递向复合壳体;复合壳体的金属材料层(铝)通过热传导方式将热量传递向复合材料层(玻璃钢);复合壳体外部主要通过热辐射和大空间自然对流这两种方式将热量传递向外界环境。流体场模型中两种组分气体的流动方式均为层流流动。
3.2 热平衡方程
热平衡过程是一个瞬态过程,与时间相依。在单位时间内,当铝导体和铝壳体产生的单位长度电阻热损耗之和与散发到外界环境的散热量相等时,达到热平衡状态[13]。由此,建立了温度场模型热平衡的基本方程式:

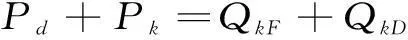
式中:Pd为单位长度单相铝导体电阻热损耗,W/m;Pk为单位长度单相铝壳体电阻热损耗,W/m;QdF为单位长度单相铝导体热辐射散热量;QdD为单位长度单相铝导体封闭空间自然对流散热量;QkF为单位长度单相复合壳体热辐射散热量;QkD为单位长度单相复合壳体大空间自然对流散热量。
3.3 共轭传热及边界条件
流体场、温度场模型是综合考虑了壳体内外两种组分气体层流流动、流体传热以及固体传热的共轭传热模型。模型充分考虑了求解域中气体主要物性参数的温度效应等。
共轭传热边界条件为:
(1)表面对表面辐射边界B1,B2,B3施加温度边界条件Ti(瞬时温度),表面对环境辐射边界B4和空气开边界B5施加温度边界条件Tamb(环境温度),环境温度为313.15 K(40 ℃);
(2)设定辐射边界B1,B2,B3,B4的表面发射率,铝表面发射率为0.3,油漆表面发射率为0.9;
(3)流体与固体边界B1,B2,B3,B4施加无滑移边界条件Vx=Vy=0。
4仿真计算结果及分析
4.1 电磁场仿真计算结果及分析
仿真模型主要尺寸及参数如表1。

表1 仿真模型主要尺寸及参数
图2为铝导体通入4 400 A电流时的电流密度分布,图3为铝壳体产生相应感应电流时的电流密度分布。两者电流大小几乎相等,电流方向相反。从图中可以看出,两者的电流密度分布呈现出明显的趋肤效应[14],铝导体电流密度分布从内侧到外侧电流密度值越来越大,铝壳体电流密度分布从内侧到外侧电流密度值越来越小。

图2 铝导体电流密度分布
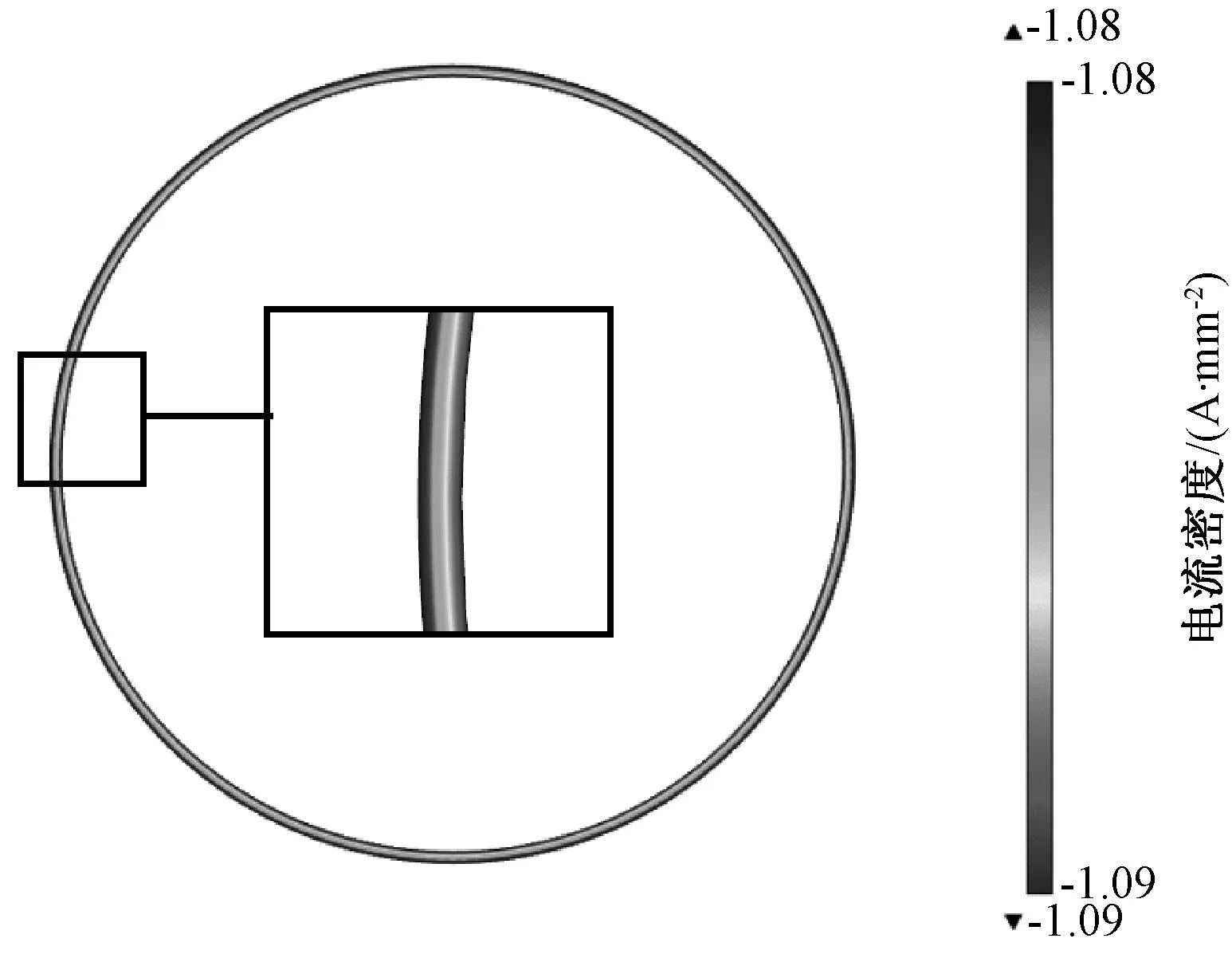
图3铝壳体电流密度分布
考虑电导率随温度变化的特性,根据电流密度分布的仿真结果,利用面积分公式得到热平衡状态下单位长度铝壳体和铝导体的电阻热损耗计算值如表2。对比传统工程计算经验公式[13]的计算结果,两者基本接近,从而验证了电磁场模型求解电阻热损耗作为热源的准确性和可行性。

表2 电阻热损耗计算值比较 W/m
4.2 流体场、温度场仿真计算结果及分析
将电磁场模型仿真求解得到的电阻热损耗作为热源,与流体场、温度场耦合计算[15],仿真求解温升瞬态过程,将得到的稳态值作为仿真结果。考虑流体的主要物性参数的温度效应。参考3.3来设置温升模型的边界条件。参照实际型式试验中的温升试验操作时间,设置瞬态温升模型的仿真热平衡时间为21 600 s,时间步长为10 s。经过仿真计算,得到流体场、温度场模型的相关仿真结果。
图4为3个温度测量点热平衡过程的温度变化曲线图,3条曲线从上至下分别为横截面上的导体最高点、壳体最高点、壳体最低点的温度变化曲线。由图4可以看出,3个测量点的温度变化趋于热平衡状态,达到相应的稳态热平衡温度。导体最高点和壳体最高点的温度一般也是GIL/GIB实际运行时导体和壳体的最高温度,可以作为判断GIL/GIB实际运行温度是否超过标准的参考温度[11]。
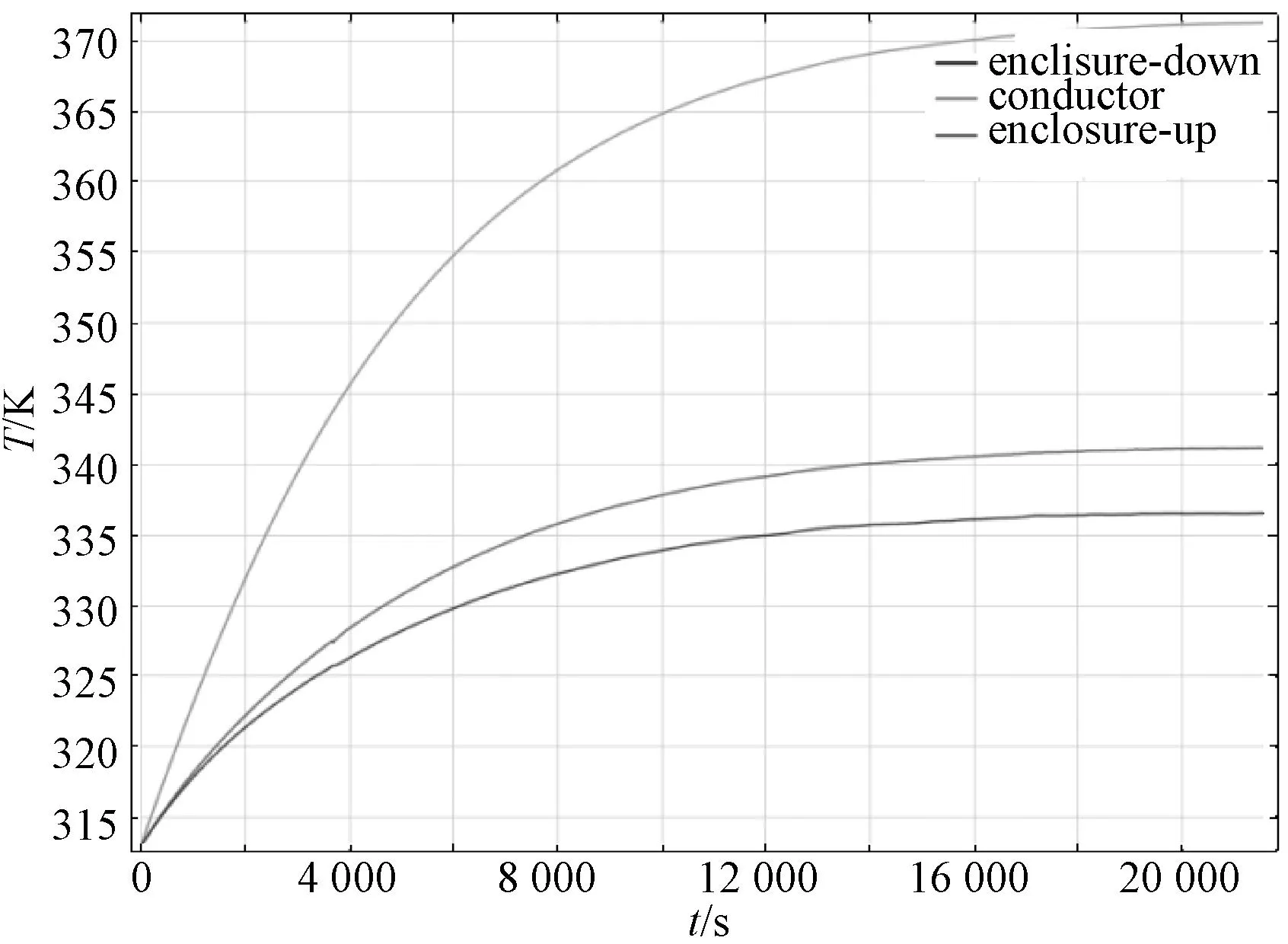
图4 测量点温度变化曲线图
表3为温度场仿真计算结果与实际型式试验中的温升试验测量结果的比较。考虑到一些不可避免的误差,3组参考温度点的仿真结果和试验测量结果基本接近。在一定程度上可以证明,该温升模型的仿真计算结果对于复合GIL/GIB试验样机的设计具有一定的理论参考意义。

表3 仿真计算和试验测量的温升结果比较 K
图5为整个仿真求解域的温度场分布。可以看出,温度场分布呈现出对称性分布;最靠近壳体外部的一层空气以及壳体正上方狭窄区域内的空气,温度明显高于空气域中其他部分。图6为GIL/GIB截面的温度场分布。可以看出,导体以及其内部气体温度场分布差异较小,可以视为等温体考虑;壳体温度场分布呈现上高下低的差异,最高点温升为28 K,最低点温升为23.4 K;导体与壳体之间的SF6气体温度场分布呈现出极其明显的上高下低的温度梯度分布特性。这主要是由于气体受热不均,在重力和浮力的共同作用下,热空气上升、冷空气下沉,从而呈现出上方温度高、下方温度低的温度分布。壳体的温度分布主要是受气体温度分布的影响。图7为整个仿真求解域的速度场分布。图8为GIL/GIB截面的速度场分布。图7中气体的流速最大为0.43 m/s,图8中气体的流速最大为0.08 m/s。图7和图8中的速度场分布均能较好的表现出两种气体的自然对流特性。自然对流传热方式作为整个模型的主要传热方式之一,是影响整个模型的速度场分布以及温度场分布的主要因素。
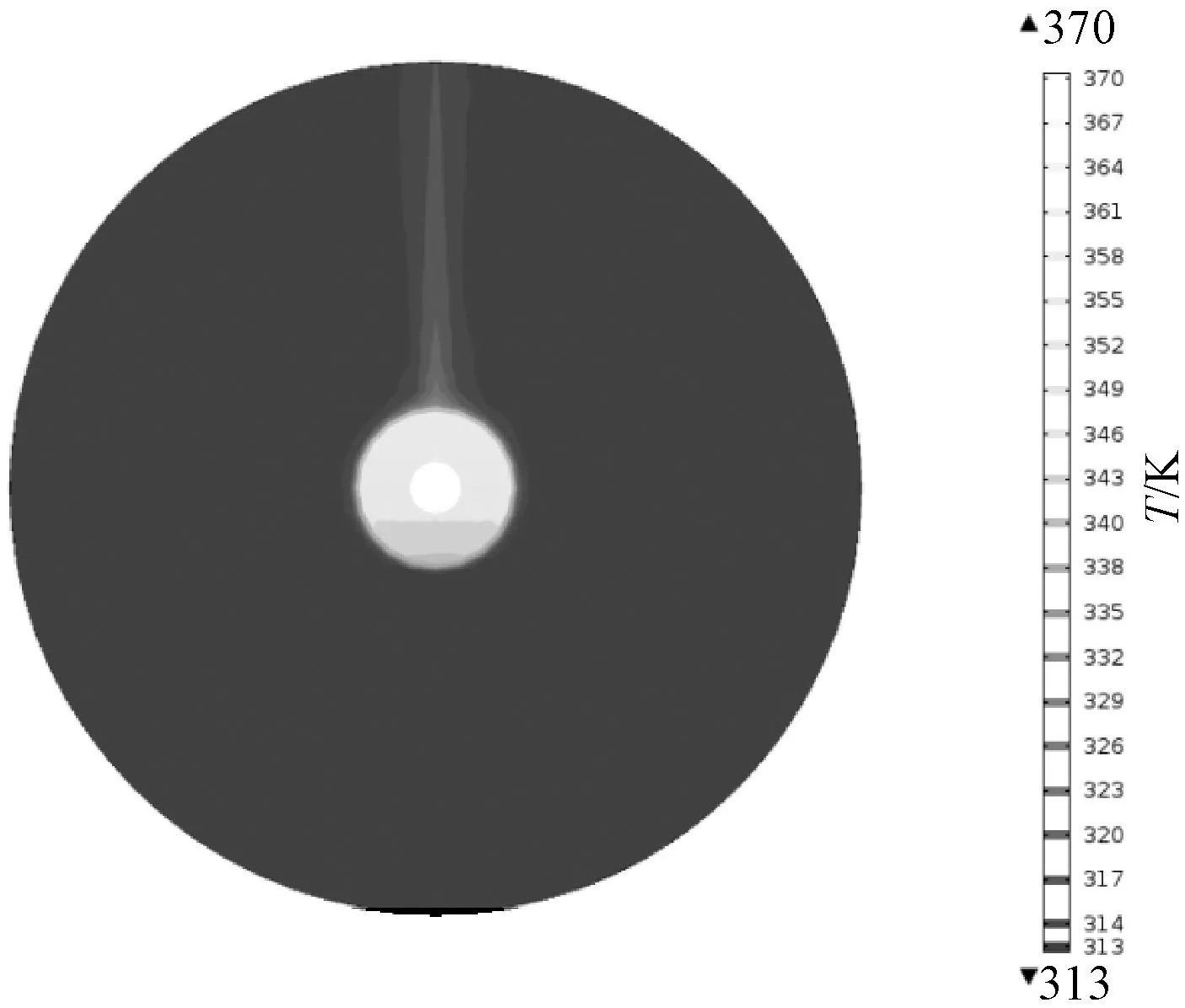
图5 仿真求解域的温度场分布

图6 GIL/GIB截面的温度场分布

图7 仿真求解域的速度场分布

图8 GIL/GIB截面的速度场分布
5结论
(1)由电磁场仿真结果可以看出,单相复合GIL/GIB截面铝导体和铝壳体的电流密度分布的趋肤效应明显,铝导体电流密度值从内到外越来越大,铝壳体电流密度值从内到外越来越小。
(2)电磁场仿真计算和传统工程计算的电阻热损耗结果十分接近,验证了电磁场模型的可行性和准确性。
(3)由流体场流体速度分布规律以及温度场的温度分布规律可以看出,自然对流传热方式是影响单相复合GIL/GIB温升模型速度场分布和温度场分布的主要因素。
(4)通过比较瞬态温升模型仿真计算结果和实际温升试验结果,验证了本文建立的瞬态温升模型的可行性和准确性,从而为复合GIL/GIB的设计、制造及工程应用提供一定的理论依据。
参考文献:
[1]Ho S L,Li Y,Lo E W C,et al.Analyses of three-dimensional eddy current field and thermal problems in anisolated phase bus[J].IEEE Transactions on Magnetics,2003,39(3):1515-1518.
[2]孔庆东,罗敬安,林福本.大电流母线的设计、制造及安装[M].北京:水利水电出版社,1988.
[3]吴晓文,舒乃秋,李洪涛,等.基于流体多组分传输的气体绝缘母线温度场数值计算与分析[J].中国电机工程学报,2012,32(33):141-147.
[4]Kim S W, Kim H H, Hahn S C,et al. Coupled finite element-analytic technique for prediction of temperature rise in power apparatus[J]. IEEE Transactions on Magnetics,2002,38 ( 2):921-924.
[5]Kim J K, Hahn S C, Park K Y, et al. Temperature rise prediction of EHV GIS bus bar by coupled magnetothermal finite element method[J]. IEEE Transactions on Magnetics,2005,41( 5):1636-1639.
[6]Eteiba M B,Aziz M M A,Shazly J H.Heat conduction problems in SF6 gas cooled-insulated power transformers solved by the finite element method[J].IEEE Transactions on Power Delivery,2008,23(3):1457-1463.
[7]Aliferov A,Dughiero F,Forzan M.Coupled magnetothermal FEM model of direct heating of ferromagnetic bended tubes[J].IEEE Transactions on Magnetics,2010,46(8):3217-3220.
[8]Ham J K, Kim Y K, Kim J S, et al. Heat transfer ingas-insulated bus bars[C]. Proceedings of the ASME 2003 Heat Transfer Summer Conference, Las Vegas, USA, 21-23 July, 2003: 453-459.
[9]李玲,吴晓文,李洪涛,等.气体绝缘母线热计算及其影响因素分析[J].电工技术学报,2012,27(9):264-270.
[10]宋帆.特高压GIS设备的涡流及其相关问题的研究[D].沈阳:沈阳工业大学,2009.
[11]GB/T 11022-2011,高压开关设备和控制设备标准的共用技术要求[S].
[12]杨世铭,陶文铨.传热学[M].北京:高等教育出版社,2006.
[13]阮全荣,谢小平.气体绝缘金属封闭输电线路工程设计研究与实践[M].北京:中国水利水电出版社,2011.
[14]鄢来君,张颖.大电流封闭母线温升计算[J].高电压技术,2008,34(1):201-203.
[15]范镇南,张德威,陈显坡,等.用电磁场和流场模型计算GIS母线损耗发热[J].高电压技术,2009,34(12):3016-3021.
Simulation and Calculation of Temperature Rise Model on New Composite GIL/GIB
Wu Quhong, Dong Lihui, Zhu Yong, Cao Donglin, Zhong Liuji
(Jiangsu Shenma Electric Co.Ltd., Nantong 226553, China)

