基于双环控制的容性逆变器控制方法研究
李向前,王旭红,李 丹,陈 坤
(长沙理工大学 电气与信息工程学院,湖南 长沙 4 10004)
基于双环控制的容性逆变器控制方法研究
李向前,王旭红,李 丹,陈 坤
(长沙理工大学 电气与信息工程学院,湖南 长沙 4 10004)
针对逆变器滤波电感电流反馈、滤波电容电流反馈存在的不足,提出反馈负荷电流的方法以改善系统性能。通过对电容特性输出阻抗逆变器建模,得出输出阻抗呈电容特性的配置方法;分析反馈负荷电流的双闭环控制,得出系统的闭环传递函数,并利用闭环极点配置方法设计控制器参数。通过MATLAB中仿真,证明由改进的控制方法控制容性逆变器,表现出动态响应更快、抗负载扰动能力更强等优点;在非线性负载时,对输出电压波形THD有很好的抑制作用。
逆变器;负荷电流;双环控制;电容;容性逆变器
0 引言
随着信息技术的不断发展,逆变器的应用领域的不断扩大,人们对其输出的性能的要求也越来越高[1,2]。目前,大部分负载都是非线性负载,当电压源无谐波成分时,会在这些负载上造成谐波电流[3~5]。谐波会导致元器件发热、增加损耗降低功率,使中线过载并导致电压和电流波形变形等,已成为现代电力系统的严重问题之一[6,7]。
逆变器输出电压谐波主要有两大来源:①逆变器本身 (主要由脉宽调制和开关效应);②电力负荷或者大电网[8~10]。因此,为了满足各电力单元的需要,逆变器的控制器必须具备优良的谐波抑制功能。逆变器输出阻抗被设计呈电容特性,通过改变虚拟电容大小有助于降低输出电压的THD。目前,逆变器的双环控制主要包括基于滤波电感电流的双环控制和基于滤波电容电流的双环控制,反馈电感电流虽然能够通过对电流限幅,实现自我保护,但在输出特性、动态响应方面差强人意;反馈电容电流满足了动态响应的要求,但在实现过负荷及对限制短路电流方面存在不足[11~13]。
本文引入积分反馈实现逆变器的电容特性,采用负荷电流正反馈的方法弥补以上两种控制方法的不足,分析该方法下闭环极点参数对系统性能的影响。通过在MATLAB中的仿真分析,证明改进的双环控制能够使快速控制容性逆变器的输出,并且输出电压谐波畸变率低、非线性负载适应能力强、动稳态性能好。
1 电容特性输出阻抗逆变器建模
为了分析方便,建立单相逆变器数学模型,采用PWM控制,配置LC滤波器,其电路模型如图1所示 (r为多种阻尼的综合影响因素,一般不大于1 Ω)。逆变器结构模型是一个典型的二阶系统,其输出特性主要取决于其配置的LC滤波器及负载特性。

图1 单相逆变器拓扑结构
在此逆变器的基础上添加控制器能实现逆变器输出特定的输出效果。数字计算和PWM转换的效应可以通过一步延迟环节e-Tss来近似,其中Ts为采样周期,添加积分环节后能实现逆变器电容特性的输出阻抗,得到控制回路被近似后的控制框图,如图2所示。

图2 容性系统电流回路近似结构图
电感电流中包含可滤波电容电流及负载电流,能够实现限制负荷电流的作用,因此可以用于构建如图2中积分控制器,从而使逆变器的输出阻抗被强制改为电容特性,并在逆变器和AC母线之间的阻抗中占主导地位。这样相当于将一个虚拟电容器与滤波电感L串联。
由于在一个开关周期内,电压的平均值:

其中,逆变器输出阻抗Zo(s)为

若电容C0足够小,则电感的影响会比较小,逆变器的输出阻抗在很宽的频率范围内都会接近纯电容特性,因此,有

其等效电路如图3所示。
积分控制器1/sC0的添加会将逆变器输出阻抗强制改为电容特性,输出阻抗伯德图如图4所示。由图4中相频曲线可以得到:在低频和高频段,输出阻抗均表现为电容性。

图3 容性逆变器等效电路

图4 电容特性输出阻抗伯德图
2 容性系统双环控制器设计
2.1 控制器设计
逆变电源采用LC型滤波器,在控制器设计过程中考虑到整个系统的动态、稳态性能及抗负载扰动能力等诸多因素,控制器采用滤波电感电流内环、输出电压外环的双环控制,并反馈负荷电流。控制器如图5所示。

图5 控制系统框图
控制原理:虚拟阻抗计算通道上添加的积分环节1/sC0和电感电流il(s)相互作用,得出逆变器电压Ui(s)在虚拟电容器上的压降,此压降与正弦参考电压及输出电压反馈信号Uo(s)相互作用下的误差信号,经过PI控制器的调节作用后作为电感电流il(s)的控制信号,该指令值再与电感电流的反馈作用后,经过放大后与PWM模块内部的载波信号作用,产生PWM控制信号,用来控制逆变器电压Ui(s),因为电感电流il(s)中包含可滤波电容电流计负载电流,因此能够实现限制负荷电流的作用。il(s)的方向是进行死区补偿的必要条件,可以对死区进行补偿。
控制器传递函数推导如下:

式中:Ur(s)为标准参考电压;Gv(s)=kvp+kvi/s为外环PI控制器;Gi(s)=kip为内环比例控制器。理论上,电压环在电压参考值要先减去虚拟阻抗上压降后,才能作为输出电压的给定参考值,电流环跟踪瞬时负荷电流的值。
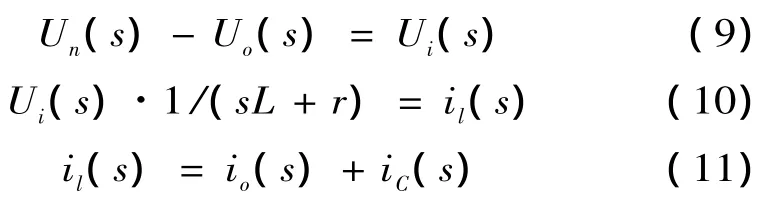
式中:iC(s)=sC·Uo(s)。
联合式 (7)~(11),得出整个系统的闭环传递函数:
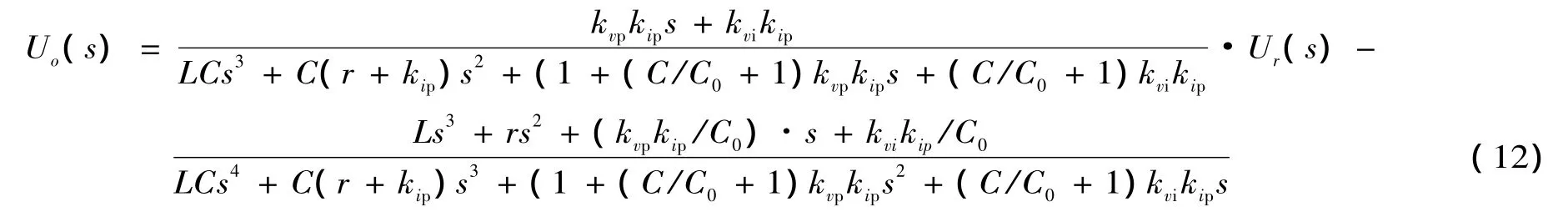
简化式 (12),得

2.2 控制器参数整定
式 (12)的闭环传递函数特征方程为

这是一个三阶系统,利用极点配置方法整定控制器参数,该方法在此不赘述,控制器参数方程为:

式中:ωn为自然震荡频率;n为正的常数;ξ为阻尼比。
2.3 闭环极点参数对系统性能影响分析
为了验证闭环极点参数ωn,n,ξ对系统性能的影响。参考阻尼比ξ=0.7,期望自然震荡频率ωn=3 500,n=10。当参数改变时,对应的控制器参数如表1所示。
改变表1中单个参数,得到其闭环传递函数伯德图,如图6~8所示 (各图中曲线1~4均表示为参数逐渐增大),图中包含2个伯德图,第1个伯德图曲线1~4的位置依次为由下向上变化;第2个伯德图幅频图中曲线1~4的位置是由上向下,相频曲线为由下向上变化。

表1 闭环极点参数改变时对应的控制器参数
(1)保持n=10,ξ=0.7不变,参数ωn=1 500,2 500,3 500,4 500(如图 6 所示),由电压环增益幅频特性得到:G的带宽随ωn从左至右变大而变宽,|G(ω0)|≈1(ω0为工作频率);由输出阻抗幅频特性得到:在中频段,Zo(s)的增益随ωn的变大而变小,log|Zo(ω0)|由-4.4 dB减小到-21.2 dB。因此,逆变器输出电压稳态误差减小,系统输出电压的总谐波失真率在非线性负载时明显降低。

图6 参数ωn对系统的影响

图7 参数n对系统的影响

图8 参数ξ对系统的影响
(2)保持ωn=3 500,ξ=0.7不变,参数n=5,10,15,20(图7),当n≥5 时,由电压环增益幅频特性得到:当n从左到右逐渐变大时,电压环增益|G(ω0)|≈1,G的带宽有小幅度的变宽;由阻抗幅频特性得到:Zo(s)在中频段的幅频特性随ωn增大而减小。因此,系统的输出特性对指令的跟踪特性不会随n变大而明显变化,但会随着n的增大,系统的抗扰动能力得到增强。在非线性负载时,逆变器输出电压总谐波失真率明显减小。
(3)保持ωn=3 500,n=10不变,阻尼比ξ=0.2,0.7,1.0,2.0(图 8)。由增益幅频特性得到:当ξ从左到右逐渐变大时,电压环增益没有特别变化,但G的带宽有所变宽,不但增强了重现输入信号的能力,而且减弱了抑制输入端高频噪声的能力;由阻抗幅频特性得到:
整个上午,我们都关在屋里。中间去个茅厕,也是有个东洋兵紧跟着,站在茅厕外面。中饭时候儿,早上那个兵又来送饭。我刚要开口,他低头小声说:“你莫为难我。我帮不了你。”把东西搁桌上就着急走了。
①在中频段,Zo(s)的增益变小,则非线性负载时逆变器输出电压的总谐波失真率降低;
②在0.5~0.7内,选定阻尼比为0.7左右,此时逆变器输出电压的稳态误差及抗负载扰动能力均比较小;
③当负载为非线性时,输出电压波形的THD低;当负载突变时,系统的动态过渡过程加快。与此同时,系统对高频噪声也有较好的抑制作用。
综上分析可得,对于闭环极点中ωn,n,ξ 3个参数,当ωn增大时,系统输出电压的稳态误差明显增大,但会随着ξ的增大而减小;当n变化时,对系统影响很小。当ωn,n,ξ均增大时,系统抗负载扰动能力增强,其中ωn,ξ的影响比较显著。并且从各参数对应输出阻抗伯德图 (图6~8中的相-频曲线)中可以直观地看出逆变器在高频和低频段呈电容特性。
3 设计实例及仿真
3.1 实验参数
为了验证容性系统在此控制器下有良好的动、稳态性能,设计1台单相容性逆变器进行仿真实验,实验主电路如图9所示。容性逆变器主要参数:直流侧电压VDC=380 V,滤波器参数L=0.43 mH,C=140 μF,额定输出电压 Uo=220 V,额定功率Pn=1.1 kW,PWM开关频率fs=20 kHz,积分器参数 C0=1 700 μF。
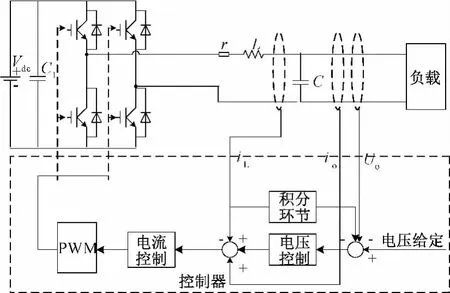
图9 实验主电路
3.2 仿真结果及分析
为了验证改进的控制器对容性逆变器有很好的暂态控制效果,仿真设置负载扰动,初始负载为额定功率负载,0.1 s时突加1.1 kW负载,0.1 s后切除负载。系统在负载扰动下负载电流变化仿真结果如图10所示,负载扰动情况下的负载端电压变化情况如图11所示。

图10 负载电流变化情况
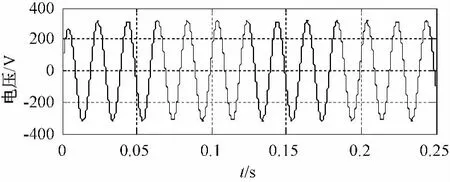
图11 负载端电压变化情况
由图10可知,在突加负载时,负载电流很快达到稳定状态,在0.2 s切除负载时,电流出现了较小的超调,约为6.54%,并且在约1 ms的时间内即恢复稳定;由图11可知,负载端电压只在突加、突减负载时出现略微变化,变化幅度不明显,并且迅速恢复平稳。
负载特性发生变化时负载电流、电压变化情况分别如图12,13所示。仿真初始设置为额定功率阻性负载,0.1 s时切换到二极管整流阻感性负载,Rload=40 Ω,Lload=1 mH。

图12 负载特性突变时负载电流变化
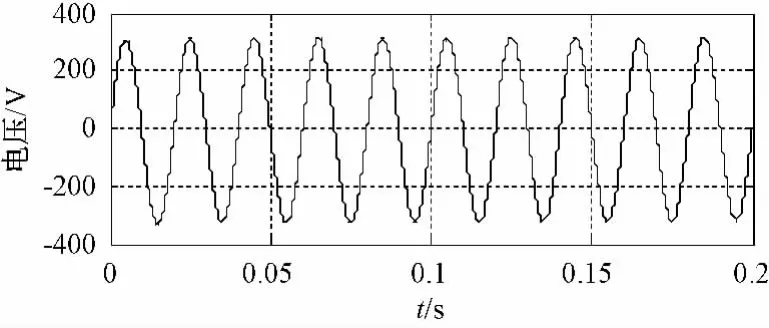
图13 负载特性突变时负载电压变化
当负载切换时,负载电流过渡平滑,无明显波动;电压变化不明显。由此可见,改进的控制器动态响应性能良好,使容性系统在应对暂态响应时具有足够的稳定性。
为了验证改进的控制器对输出电压波形畸变的抑制能力,利用SIMULINK中POWERGUI模块对输出波形进行傅里叶分析,输出波形频谱如图14所示。
由于逆变器输出电压的THD主要取决于谐波频率处逆变器的输出阻抗,因此,该文研究的逆变器输出阻抗被设计成电容特性,可以通过设置虚拟电容C0的大小来改善输出电压的THD(仿真参数 C0已选取最优[14])。线性负载条件下,输出波形THD为0.23%;在二极管非线性负载下,输出波形的THD仅为0.33%,满足电压质量要求。
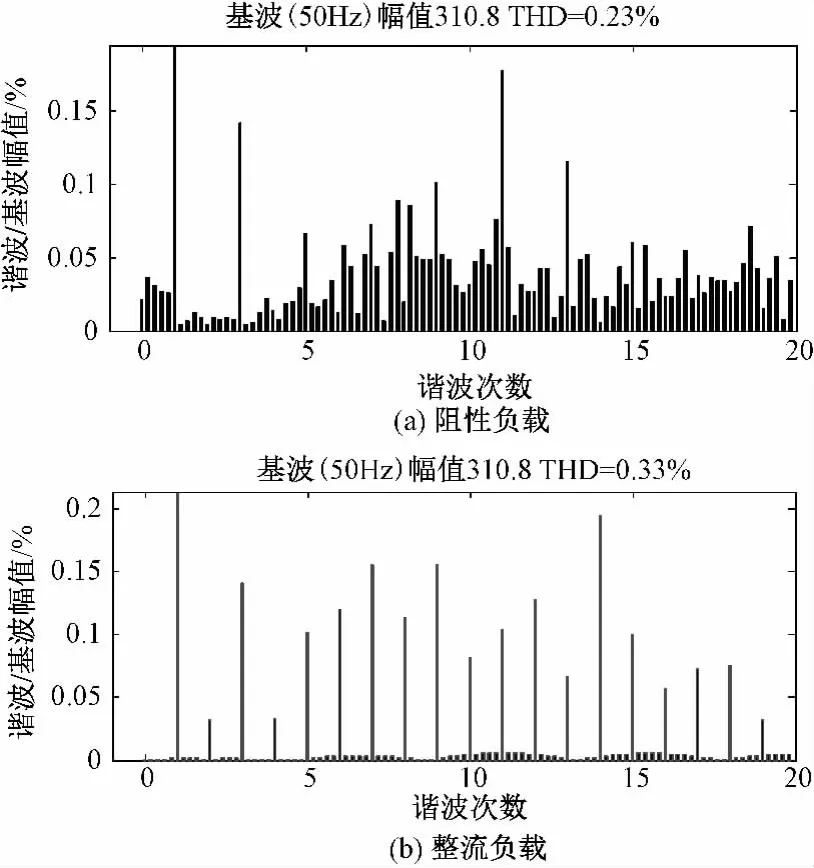
图14 线性、非线性负载输出电压频谱
4 结论
通过研究逆变器电容特性控制器配置方法,引入积分反馈,实现逆变器电容特性。采用负荷电流正、反馈弥补传统双环控制方法的不足。仿真结果表明:反馈负荷电流控制器能同时兼顾容性系统的动稳态性能,通过闭环极点参数配置方法配置控制器参数,使容性系统的非线性负荷适应能力、动态响应能力进一步加强,并且降低输出电压的THD。
[1]Zhong Q C,Zeng Y.Can the output impedance of an inverter be designed capacitive[C].The 37th Annual Conference on IEEE Industrial Electronics Society(IECON),Melbourne,Victoria,Australia,7 -10 November,2011:1220-1225.
[2]Micallef A,Apap M,Spiteri-Staines C.Cooperative control with virtual selective harmonic capacitance for harmonic voltage compensation in islanded microgrids[C].The 38th Annual Conference on Conference on IEEE Industrial Electronics Society(IECON),Montreal,QC,Canada,25-28 October,2012:5619-5624.
[3]李鑫,姚勇涛,张逸成,等.采用电容电流内环的逆变器双环控制研究 [J].电气传动,2008,38(2):23-26.
[4]许津铭,谢少军,唐婷.基于极点配置的LCL滤波并网逆变器电流控制策略 [J].电力系统自动化,2014,38(3):95-100.
[5]吕永庆,赵军红,张珍敏.基于极点配置的逆变器双环控制方案 [J].现代电子技术,2009,32(22):176-179.
[6]王淑惠,彭立,康勇,等.基于极点配置PI数字双环PWM逆变器的研究 [J].电源技术应用,2008,11(9):34-39.
[7]Zhong Q C,Zeng Y.Control of inverters via a virtual capacitor to achieve capacitive output impedance[J].IEEE Transactions on Power Electronics,2014,29(10):5568-5578.
[8]杨淑英,张兴,张崇巍,等.LCL滤波电压源并网逆变器多环控制策略设计 [J].电力系统自动化,2011,35(5):66-70.
[9]徐志英,许爱国,谢少军.采用LCL滤波器的并网逆变器双闭环控制入网电流控制技术 [J].中国电机工程学报,2009,29(27):36-41.
[10]刘俊,杨帆,张一彦.电网畸变条件下基于LCL型滤波的STATCOM电流控制策略研究[J].电力与能源,2014,35(6):665-671.
[11]彭勇,李倩.微电网并网运行时的电压稳定控制 [J].电力建设,2014,35(6):56-62.
[12]吴桂良,田永贵,李小明,等.三相PWM整流器的鲁棒反演控制器设计 [J].电力科学与工程,2014,30(12):46-49.
[13]罗军,姚蜀军.三相逆变器的单环与双环控制比较研究 [J].电力科学与工程,2014,30(10):1-5.
[14] Micallef A,Apap M,Spiteri-Staines C,et al.Selective virtual capacitive impedance loop for harmonic voltage compensation in islanded microgrids[J].The 39th Annual Conference on IEEE Industrial Electronics Society(IECON),Melbourne,Victoria,Australia,10 -13 November,2013:7968-7973.
Research on the Capacitive Inverter Control Method Based on Dual-loop
Li Xiangqian,Wang Xuhong,Li Dan,Chen Kun
(College of Electrical and Information Engineering,Changsha University of Science and Technology,Changsha 410004,China)
To tackle at the deficiency of the inverter in filter inductor current feedback and filter capacitor current feedback,a method of load current feedback is proposed to improve the performance of the system.First the configutation method of output impedence was obtained through the modeling of output impedance.Then,the double closed-loop control of the load current feedback was analyzed to get the dosed lop transfor function and controuer parameters were set by using closed-loop of pole placement method.Finally,the simulation was conducted in Matlab and the results proved that the improved control method,boosting the advantages of faster dynamic response and stronger anti-disturbance,was better at controlling the capacitive inverter and that it had a good inhibitary effect on the voltage output waveform THD in nonlinear load.
inverter;load current;the dual-loop control;the capacitor;the capacitive inverter
TM851
A
10.3969/j.issn.1672-0792.2015.06.002
2015-03-26。
湖南省高校创新平台开放基金项目 (2014-2017);长沙市科技项目 (k1403041-11)。
李向前 (1989-),男,硕士研究生,研究方向为微网运行与控制,E-mail:lxq307307@163.com。

