微网风电容量投资双层优化
周 鹏,易国伟,尹 昆,翟云峰,叶中行
(1.长沙理工大学 电气与信息工程学院,湖南 长沙 410004;2.南方电网湛江供电公司,广东 湛江 524005)
微网风电容量投资双层优化
周 鹏1,易国伟1,尹 昆2,翟云峰1,叶中行1
(1.长沙理工大学 电气与信息工程学院,湖南 长沙 410004;2.南方电网湛江供电公司,广东 湛江 524005)
基于双层优化思想,研究微网中独立投资商的风电容量投资问题,建立了风电投资商和微网管理方的双层优化模型。模型中同步考虑了风电安装后的调度,可使投资决策更加合理。上层优化模型中,考虑了一定的风电投资补贴,用场景刻画风电的随机性,通过决策风电安装容量和安装后的风电调度,使风电投资商的利润最大;下层优化模型中,在满足微网系统负荷需求的前提下,使微网供电成本最低。用Karush-Kuhn-Tucker最优化条件 (KKT)将双层优化问题转化为单层优化问题,利用分支定界算法求解。最后对某一微网系统进行数值仿真,验证了所提模型的合理性。
风电容量投资;风电调度;投资补贴;微网;双层优化
0 引言
进入21世纪以来,环境污染和能源危机等问题日益突出,可再生分布式电源开始获得人们关注并快速发展,其中风能的发展最为迅速。风力发电技术相对成熟、可大规模开发并且有较好的商业化前景[1]。微网是联结分布式电源和配电网的较好纽带,能较好发挥分布式电源的效用[2,3]。为合理有效的利用风能资源,研究微网中风电的投资规划问题十分必要。
对于电源投资问题,很多学者进行了相关研究,其中大部分研究对象是针对常规电源[4~6]。然而,风电投资成本大,上网电价较高,加之风电的随机特性,这使得风电投资和常规电源投资有很大的区别。文献 [7]分别站在投资和运行的角度分析风电项目经济性,提出应对风电项目采取相应的补贴政策。文献 [8]首先确定分布式电源的候选安装位置集合,然后分别以分布式电源单位成本收益和其接入后改善电网所得收益最大为目标,确定分布式电源的类型和安装容量,模型中对可再生能源给予一定的电价补贴。文献[9]建立风电项目投资决策模型,为风电投资商选择最佳投资时机,研究了风电电价补贴水平对投资决策的影响。文献 [10]对一个具体给定的系统网络,在满足线路安全约束的情况下,确定系统网络中风电的最大渗透功率。文献 [11]以风电投资商利润最大为目标,研究电力市场环境下的风电投资问题。文献 [12]分别以投资组合成本最低和投资组合风险最小为目标,首先建立常规发电机投资组合模型,然后将风电看做负负荷引入到模型中,确定风电容量。
随着社会发展,电力系统结构愈加复杂,系统优化往往需要分层协调决策,双层优化开始得到人们关注。双层优化是具有两层递阶结构的优化问题[13],上下层之间相互联系,可得到一个各方面协调的解。双层优化模型已在电力系统很多方面得到应用,如无功优化、输电网规划、机组组合问题、检修计划优化等等。目前,双层优化理论在电力系统中的应用尚处于初步阶段,推广双层优化在电力领域的应用有着切实意义。
将微网中风电的投资规划和微网管理者分离,更有利于合理利用风能资。基于以上论述,本文建立了风电独立投资商和微网管理方双层优化模型。用分段年负荷持续曲线近似表示负荷在未来一年的分布情况,上层考虑风电投资商利益,模型中给予风电投资商一定的投资补贴,用场景刻画风电的随机特性,目标为风电年平均售电收益减去年度风电投资成本最大。下层考虑微网管理方利益,目标为微网年平均供电成本最低。微网中已含有可控分布式电源 (如柴油机组、微型燃气轮机等)、公共电网供电,还包含一定的可中断负荷 (Interruptible Load,简写为IL)。
1 风电投资双层优化模型
本文考虑风电投资商和微网管理方两个不同优化主体利益,既优化风电投资所得利润,也优化微网供电成本。风电容量投资和风电调度相互影响,加之风电的投资成本较大,在决策风电安装容量的同时考虑风电安装后的调度问题,可使决策结果更加合理。上层优化考虑风电投资商,目标为风电年均售电收益减去年度风电投资成本最大,变量为风电安装容量和风电在各负荷需求区的调度量,并将风电调度的决策方案传递给下层。下层优化考虑微网管理方,在风电调度决策已知的情况下,通过优化其它供电源出力,使微网年均供电成本最低,并将由下层功率平衡等式得到的风电电价返回给上层模型。上层模型根据此电价再次优化,如此反复交替,直至得到最优解。此模型以风电投资商利益为主体,同时兼顾了微网供电侧利益。
1.1 上层优化模型
本文上层优化模型站在风电投资商角度,目标为风电投资年平均利润最大。用场景刻画各负荷需求区可用风能的随机性,电价采用边际电价,风电投资利润表示为风电年平均售电收益减去年度风电投资成本,为提高风电投资商投资积极性,给予风电投资商一定的投资补贴。
(1)目标函数
上层优化的目标为风电年平均投资利润最大,表达为年均售电收益减去年度投资成本最大:
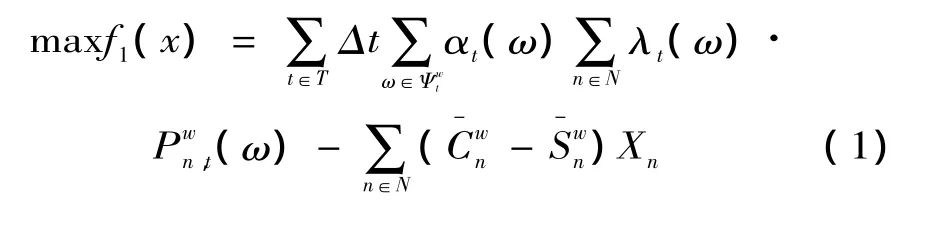
其中:

式中:f1表示风电年均投资利润;x为上层决策变量;T表示负荷需求区集合;Δt表示负荷需求区t的时间长度;表示负荷需求区t的场景集合;αt(ω)表示负荷需求区t中场景ω所占权重;N为风电安装点集合;λt(ω)表示负荷需求区t中场景ω时的风电电价;(ω)表示负荷需求区 t中 ω场景时安装点n的风电调度出力;表示安装点n的年度风电投资成本;表示安装点n的风电投资年补贴水平;Xn表示安装点n的风电安装容量。
(2)约束条件
①风电出力约束:

②风电投资预算约束:

式中:kn,t(ω)为负荷需求区t中场景ω时安装点n的风电力度;kn,t(ω)Xn表示负荷需求区t中场景ω时安装点n的可用风能;为安装点n的单位风电投资成本;为风电的投资预算。
1.2 下层优化模型
下层优化模型考虑微网管理侧利益,目标为年平均供电成本最低。风能的调度由上层决策,在满足供电靠靠性的前提下,微网根据上层给出的风电出力情况决策其它供电源出力,进而确定边际电价即为风电的购买价格。
(1)目标函数
下层优化的目标为微网系统年均供电成本最低,微网供电成本由四部分组成:公共电网购电成本、可控分布式电源发电成本、购买可中断负荷成本、购买风电成本。目标函数表达式如下:
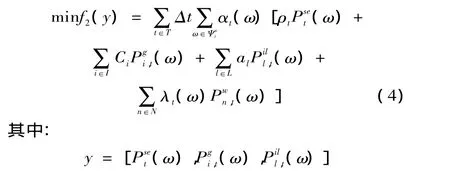
式中:f2表示微网年均供电成本;y表示下层决策变量;ρt表示负荷需求区t的公共电网购电电价;(ω)表示负荷需求区t中场景ω时从公共电网购买的功率;I为可控分布式电源集合;Ci表示可控分布式电源i的发电成本;(ω)表示负荷需求区t中场景ω时的可控分布式电源i的出力;L表示IL用户集合;al为对第l个IL用户中断供电的补偿价格,采用事后高价赔偿方式管理IL[14];(ω)表示负荷需求区t中场景ω时的第l个IL用户负荷切除量;
(2)约束条件

式中:Pd,t表示负荷需求区 t的负荷需求功率;λt(ω)为负荷需求区t中场景ω的功率平衡约束的拉格朗日系数,为风电的价格,亦常被称为节点边际电价 (Locational Marginal Prices,简写为LMPs)[15];P为公共电网的最大输入功率;(ω)(ω)分别为负荷需求区t中场景ω时公共电网输入功率下限、上限不等式对应的拉格朗日系数;P,P分别为可控分布式电源出力的最小值和最大值;(ω),(ω)分别为负荷需求区t中场景ω时可控分布式电源i出力下限、上限不等式对应的拉格朗日系数;为第 l个 IL 用户的合同容量;(ω)(ω)分别为负荷需求区 t中场景ω时第l个IL用户负荷切除量下限、上限不等式对应的拉格朗日系数。
2 双层优化模型的求解
由于本文下层优化模型具有连续性和线性特征 (凸规划),本文利用KKT条件将双层优化问题转化为一个带平衡约束的单层优化问题 (Mathematical Programs with Equilibrium Constraints,简写为MPEC)[16]。转换后的MPEC模型如下:

对于形如α·κ=0,α≥0,κ≥0的非线性表达式,可以线性化为:α≤Mγ,κ≤M(1-γ),γ∈{0,1},M 为足够大常数[17]。由此,MPEC 模型中的非线性互补松弛条件 (19)~(24)可转化为线性约束,转为:

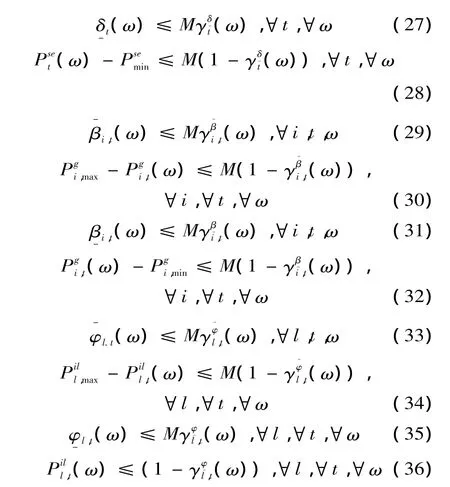
至此,MPEC模型约束已全部线性化,现整理出最终模型如下:

3 数值仿真
3.1 测试系统及数据
以某一地区微网为例,进行仿真分析。微网供电由公共电网、3台可控机组、3个可中断负荷用户、风机4部分共同承担。用分段年负荷持续曲线近似表示负荷1年的分布情况,分为8个负荷需求区,每个负荷需求区负荷大小为一个定值,负荷大小等于负荷需求水平乘以年峰荷,负荷需求水平由微网负荷历史数据可得。风电安装位置为一个事先选定的安装点,此安装点的可用风能大小表示为风力强度与安装容量的乘积。为刻画风速的随机特性,对于每个负荷需求区,将风力强度分为高、中、低3个场景,为方便计算,取每个风力强度场景对应的概率为1/3。
微网年峰荷为300 MW,负荷需求水平、风力强度相关数据参考文献 [ 11],并做了一定修改,如表1所示。公共电网的最大输入功率P为40 MW,各负荷需求区公共电网电价见表1。3台可控分布式电源的P分别为5,5,5 MW,P分别为50,70,100 MW,发电成本Ci分别为45,55,65$/MW·h。3个可中断负荷的合同容量P分别为10,15,20 MW,补偿价格al分别为80,85,95$/MW·h。风电的投资成本 C为106$/MW,投资预算C为5×108$,考虑资本回收期 k为 15年,折现率 r为 8%,由可得投资回收系数为11.68%,得到年度风电投资成本为116 800$/MW,风电投资年补贴水平取为年度风电投资成本的一定比例,取10%。

表1 各负荷需求区负荷需求水平、风力强度及电网电价
3.2 仿真结果及分析
根据以上数据,利用matlab2009a,yalmip工具箱结合cplex12.2,采用分支定界算法求解转化后的模型,得到风电安装容量为297.74 MW,上层目标函数值为4.10 M$,下层目标函数值为95.08 M$,各负荷需求区、场景下的风电调度量、风电电价分别见表2、表3。

表2 各场景下风电的调度

表3 各场景下风电电价
从表2和表3中可以看出,同等条件下,风电调度值越大对应的风电电价越小 (有时持平)。因此,在对风电调度决策时,需要考虑风电调度对风电电价带来的影响,方能使售电收益最大化。
3.3 参数变化对结果的影响
(1)补贴水平变化对结果影响
由于风电投资成本较大,补贴水平变化对结果有较大影响。当风电投资年补贴水平变化时,对应的风电安装容量、风电投资利润以及微网运行成本如图1和图2所示。

图1 不同补贴水平下的风电安装容量

图2 不同补贴水平下的上下层目标函数值
从图1和图2中可知,当补贴水平低于70%时,随着风电补贴水平增加,风电安装容量随之增大,风电的投资利润增加,微网运行成本下降。这是由于补贴水平增加相当于降低了风电投资成本,投资商将增大安装容量以提高利润,安装容量变大使风电调度量增加,这必然造成风电电价下降,进而降低微网运行成本。由于受风电投资预算限制,当补贴水平为70%时风电安装容量为500 MW,已达预算上限,补贴水平继续增加时,风电安装容量保持不变。此时,由于风电安装容量固定不变,微网最优供电调度策略相同,微网运行成本保持不变,但由于补贴水平增加,进一步降低了风电投资成本,风电利润递增。
当忽略投资预算约束时,不同补贴水平下风电安装容量、风电投资利润以及微网运行成本如图3和图4所示。

图4 不同补贴水平的上下层目标函数值 (不计预算)
图3与图1、图4和图2分别对比发现,补贴水平小于等于50%时,有无投资预算限制,风电安装容量、风电投资利润、微网运行成本结果相同,这是由于此时风电最优安装容量尚未达到投资预算上限。从图3和图4可知,当补贴水平为70%,90%,100%时,由于无投资预算限制,风电安装容量均大于500 MW,并随着补贴水平的增加进一步增大,对应的风电投资利润递增,微网运行成本下降,且忽略投资预算后对应的风电利润大于计及预算时的利润。
当补贴水平达为100%时,相当于风电已没有投资成本,由于也没有投资预算约束,风电投资商必然期望安装的风电能覆盖全部负荷。图3中投资补贴为100%时的对应点表示此时风电的最优安装容量的最小值,安装容量大于此点数值时,风电利润和微网成本保持不变均为此时最优结果。
由上可知,投资补贴水平对风电投资结果有较大影响。因此,政府应综合考虑微网和投资商两方,制定合理的风电补贴政策。
(2)风电力度变化对风电投资的影响
风电力度变化对风电安装容量和风电投资利润的影响如表4所示。

表4 风电力度对安装容量和利润影响
同等条件下,降低风电力度相当于降低了风电的可用风能,这将对风电投资商造成消极影响。当风电力度降低10%时,风电安装容量下降。当风电力度降低20%时,风电投资商不再投资风电。当风电力度提高时,风电投资商将增加投资力度,投资容量增加。从表4中看出风电力度提高20%时比提高10%时的安装容量小,这是由于综合考虑投资成本、风电调度和风电电价因素,此安装容量时风电利润最大。从表4中可以看出,随着风电力度的提升,风电投资利润总是增加的。
风电力度的增加,很大程度上提高了风电投资商利润,由此可知,选择风力强度较大的安装点十分重要。
(3)公共电网电价变化对结果影响
各负荷需求区公共电网电价 ($/MW)变为80,68,58,51,44,39,34,25,其他参数不变,得到风电安装容量为249.46 MW,风电利润为2.98 M$,微网运行成本为92.14 M$。各场景下风电电价如表5所示。
与原数据仿真结果对比可知,公共电网电价下降,导致风电安装容量减少、风电投资利润下降、微网运行成本降低。负荷水平不变的情况下,由于风电采用边际电价,公共电网电价降低将导致风电电价的下降,风电投资商将减少投资力度,安装容量和风电利润均减少。由表5和表3对比可知,公共电网电价降低使风电电价呈下降趋势,微网从公共电网和风电处购买电能电价均降低,微网运行成本下降。

表5 电网电价变化时各场景风电电价
(4)安装容量对风电年平均电价和微网运行成本影响
安装容量的不同将导致风电调度的变化,由于风电采用边际电价,这将引起风电电价的波动,进而造成微网供电成本的变化。安装容量对风电年平均电价和微网供电成本的影响如图5和图6所示。
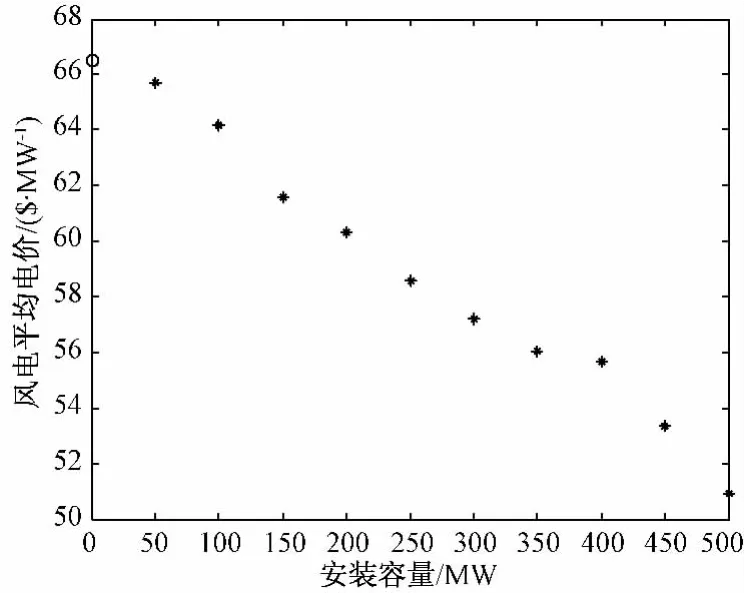
图5 安装容量对风电平均价格影响
由于风电电价采用边际电价,风电安装容量增加引起风电调度量的上升,在负荷不变的情况下,这将使风电电价下降,如图5所示,随着风电安装容量的增加风电平均电价下降。图5中圆圈表示风电安装容量趋于零时风电平均电价,即无风电投资时微网系统的边际电价。由图6看出,随着安装容量增加,微网供电成本下降,这是由于安装容量的增加使风电平均电价下降,进而微网供电成本降低。

图6 安装容量对微网供电成本影响
4 结论
由于风电投资成本较大,合理安装风电容量对风电投资商至关重要。本文建立了风电投资商、微网管理方双层优化模型,模型在最大化风电投资利润的基础上优化微网供电成本。模型中考虑对风电项目补贴,分析了不同补贴水平对风电投资和微网供电成本的影响,并对比了投资预算对优化结果的影响。同时,分析了风电力度、公共电网电价等因素对风电投资决策的影响,并分析了安装容量对风电电价和微网供电成本的影响。本文所提模型可以为微网系统中风电投资商决策风电安装容量提供一定参考。接下来,需要进一步研究风电安装点选址、系统运行安全性以及在系统中考虑储能装置等。
[1]魏显菲.我国风力发电开发现状及展望 [J].商业经济,2010,(24):21-23,33.
[2]王成山,肖朝霞,王守相.微电网综合控制与分析[J].电力系统自动化,2008,32(7):98-103
[3]杨新法,苏剑,吕志鹏,等.微电网技术综述 [J].中国电机工程学报,2014,34(1):57-70.
[4]Botterud A,Ilic M D,Wangensteen I.Optimal invest-ment in power generation under centralized and decentralized decision making[J].IEEE Transactions on Power Systems,2005,20(1):254 -263.
[5]Wang J H,Shahidehpour M,Li Z Y,et al.Strategic generation capacity expansion planning with incomplete information [J].IEEE Transactions on Power Systems,2009,24(2):1002-1010.
[6] Rider M J,Lopez-Lezama J M,Contreras J,et al.Bilevel approach for optimal location and contract pricing of distributed generation in radial distribution systems using mixed-integer linear programming [J].IET Generation,Transmissionand Distribution, 2013, 7(7):724-734.
[7]王正明,路正南.风电项目投资及其运行的经济性分析 [J].可再生能源,2008,26(6):21-24.
[8]张立梅,唐巍,王少林,等.综合考虑配电公司及独立发电商利益的分布式电源规划 [J].电力系统自动化,2011,35(4):23-28.
[9]曾鸣,李晨,刘超,等.考虑电价补贴政策的风电投资决策模型与分析 [J].电力系统保护与控制,2012,40(23):17-23.
[10] Burke D J,O’Malley M J.Maximizing firm wind connection to security constrained transmission networks[J].IEEE Transactions on Power Systems,2010,25(2):749-759.
[11] Baringo L,Conejo A J.Wind power investment within a market environment[J].Applied Energy,2011,88(9):3239-3247.
[12]曾鸣,张徐东,田廓,等.考虑风电并网的发电容量投资组合优化模型 [J].电网技术,2011,35(12):153-159.
[13]王广民,万仲平,王先甲.二 (双)层规划综述[J].数学进展,2007,36(5):513-529.
[14]张明锐,陈洁,杜志超,等.考虑交互功率控制的微网经济运行 [J].中国电机工程学报,2014,34(7):1013-1023.
[15] Orfanogianni T,Gross G.A general formulation for LMP evaluation [J].IEEE Transactions on Power Systems,2007,22(3):1163-1173.
[16]Luo Z Q,Pang J S,Ralph D.Mathematical programs with equilibrium constraints[M].Cambridge(UK):Cambridge Univisity.Press,1997.
[17] Amat J F,Mccarl B.A representation and economic interpretation of a two-level programming problem [J].Journal of Operational Research Society,1981,32(9):783-792.
A Bilevel Optimization Problem for Wind Power Capacity Investment in Microgrid
Zhou Peng1,Yi Guowei1,Yin Kun2,Zhai Yunfeng1,Ye Zhonghang1
(1.College of Electrical and Information Engineering,Changsha University of Science and Technolgy,Changsha 410004,China;2.Zhanjiang Power Supply Company,Zhanjiang 524005,China)
Based on the idea of bilevel optimization,this paper discusses the problem of the capacity of wind power is invested by an independent investor in a microgrid.A bilevel optimization model which combines the wind power investor and microgrid’s manager together.In order to make the investment decision more reasonable,the wind power scheduling is also considered in this model.In the upper-level,the investor decides the installed capacity and wind power scheduling to maximize his profit.And the subsidies can also be taken into consideration.The stochastic characteristics of wind power are expressed by scenarios.The lower-level aims to minimize the cost of microgrid power supply on the condition of meeting the system’s load demand.By the use of the Karush-Kuhn-Tucker optimality conditions,the bilevel model has been transformed into a single level optimization.Then,the single level optimization model can be solved by branch and bound algorithm.Finally,a numerical simulation of the microgrid system is used to verify the rationality of the proposed model.
wind power capacity investment;wind power scheduling;investment subsidies;microgrid;bilevel optimization;
TM615
A
10.3969/j.issn.1672-0792.2015.06.006
2015-04-05。
周鹏 (1992-),男,硕士研究生,研究方向为风电规划与运行,电力系统运行与控制,E-mail:1210021263@qq.com。

