基于样本熵的AGC指令复杂性分析
张舒铠,刘鑫屏,张锐锋
(1. 华北电力大学 控制与计算机工程学院,河北保定071003; 2. 贵州电力试验研究院,贵州贵阳550002)
基于样本熵的AGC指令复杂性分析
张舒铠1,刘鑫屏1,张锐锋2
(1. 华北电力大学 控制与计算机工程学院,河北保定071003; 2. 贵州电力试验研究院,贵州贵阳550002)
摘要:电网通过“两个细则”考核标准对机组AGC补偿服务方面进行评价,其标准仅从AGC可用率和AGC调节性能指标两方面进行评价并以此为基准来补偿火电机组在调峰、调频方面所做出的贡献,但是其AGC性能指标计算方式仍不能完全体现复杂指令信号对火电机组造成的不利影响以及火电机组为此所付出的代价。采用样本熵方法对AGC指令的复杂性进行分析。在使用样本熵方法对几组不同频率下的典型信号进行复杂性分析,验证此方法有效性和准确性的基础上,对西北电网660 MW超临界机组AGC指令进行复杂性分析。分析的AGC指令同时具有高速率大幅度单向变化、高速率中等幅度正反向变化、高速率小幅度频繁波动等特征。数据分析结果表明:样本熵能较准确地反映AGC指令的复杂性,与现场运行实际情况较为吻合。
关键词:自动发电控制;样本熵;复杂性;AGC指令
中图分类号:TM621
文献标识码:A
DOI:10.3969/j.issn.1672-0792.2015.06.008
收稿日期:2015-04-23。
基金项目:国家重点基础研究发展计划资助项目(973项目)(2012CB215203)。
作者简介:张舒铠(1991-),男,硕士研究生,研究方向为大机组智能优化控制,E-mail:zskalqkkkk@126.com。
Abstract:Power grid appraises the AGC compensation services throught “two rules” the AGC availability and the AGC adjusted performance measurement evaluation. Based on the two rules, the AGE compensation services can compensate for the thermal power generating unit contribution in terms of peak load and frequency modulation. But the AGC performance index calculation can not fully reflect the complex signals of adverse effects of thermal power generating units or the cost of thermal power units. Thus this essay employs sample entropy method to analyze the complexities of AGC instructions. The complexity analysis of typical signals of different frequencies has been conducted through sample entropy method. And the validity and accuracy of this method have been verified. Based on these previous research findings, this essay then analyzes the 660 MW supercritical unit AGC instructions the Northwest power grid. The results show that AGC instructions high data rate one-way change, high-speed medium range forward and reverse changes, high-speed small amplitude fluctuation. It has been found that the sample entropy can accurately reflect the complexities of AGC instructions, and match the running reality.
Keywords:automatic generation control;sample entropy;complexity;AGC instructions

0引言
随着用电侧负荷日趋复杂及可再生能源发电的并网,为保证电网安全稳定的运行,需要调度调节能力良好的火电机组来维持电网频率稳定。由于火电机组自身不适合做快速的调峰调频,AGC(自动发电控制)指令的变化过于频繁,对整个火力发电过程的安全性、经济性和环保性都具有极大负面影响。电网需要采取良好的激励机制来区分各火电机组参与调峰调频所做出的贡献值及各机组的完成情况,即“以质论价”。目前,电网主要的区分依据是“两个细则”考核标准。以华北电网“两个细则”为例,它从AGC可用率和AGC性能两方面进行了一系列的量化考核,但在其实施后出现了诸如“两个细则”要求与节能要求相悖,或是电厂为快速响应AGC指令不计设备严重磨损导致设备寿命大大降低等问题。因此,分析发电任务的难易程度即机组接收到的AGC指令的复杂性对区分不同机组在调峰调频中的贡献有着重要的意义。
对于不同的火电机组由于调度时采用的 “Off-regulated模式”和“Regulated模式”的不同,其接收到的AGC指令信号也不同。为了确保公平,就应该对AGC指令进行分析。文献[1]提出用控制区总发电功率与基准出力之差和频率误差的相关系数作为控制区AGC性能的指标。文献[2]提出了将AGC机组调节效能划分成3个效能系数并使用其对机组的调节性能进行定量评估。文献[3]提出了一种新型的控制性能评价标准调度控制性能标准DCPS及与之相适应的AGC控制模式。国外的学者们则多采用的是北美可靠性公司(NERC)提出的CPS标准来对AGC机组进行评价。
构成宇宙各个层次事物系统中,都证实存在着复杂性[4]。复杂性问题贯穿了科学里所有的领域。科学研究领域中的“复杂性”一词在不同的学科领域中的定义也不尽相同[5]。目前一个较为综合的复杂性定义指的是混沌性的局部与整体之间的非线性形式。为衡量非线性时间序列的复杂性,Pincus[6]研究出了近似熵的方法,而样本熵则是在近似熵的基础上克服了近似熵的一些缺点,从而能更加精确的计算时间序列的复杂性。
由于AGC指令信号具有随机波动特性,因此本文采用样本熵的方法来分析AGC指令信号的复杂性。样本熵在继承了近似熵所有优点的同时,降低了近似熵引入自身数据比较的偏差,和近似熵相比具有更好的相对一致性。目前样本熵方法已经在生物心电信号、脑电波信号、机械轴承振动信号等复杂信号的检测中成功应用。本文选取几种典型的指令信号来验证样本熵运用于AGC信号的可行性,再使用样本熵方法来分析AGC指令信号的复杂性。
1典型指令信号复杂性分析
1.1 样本熵
Pincus从衡量非线性时间序列复杂性的角度提出了近似熵[6]的概念,并将其成功应用于生物时间序列的复杂性研究,但该方法存在矢量自身匹配计入统计量而导致其计算结果产生偏差的缺陷。为克服近似熵计算中存在的缺陷,后来Richman提出了一种改进的复杂性测量方法——样本熵[7]。样本熵与近似熵的物理意义相同,具备相对一致性,但比近似熵更符合理论性。
样本熵的大小反映了非线性动力学系统产生新模式的概率,可以用来定量描述系统的规则度和复杂度。样本熵值越低,说明序列自我相似性越高,该序列中产生新模式的概率越低,从而可知该时间序列越简单;反之,样本熵值越大,说明该时间序列越复杂。和近似熵一样,样本熵只需要较短的数据,一般选取1 000点就可以达到分析的目的,同时可以保证很好的一致性。
样本熵具体算法步骤如下[8~10]:
(1)设原始数据为{x(1),x(2),…,x(N)},共N点。
将序列X(i)按顺序组成一组m维矢量:


(1)
(2)定义X(i)与X(j)之间的距离d[X(i),X(j)]为这两个矢量对应元素中差值最大的一个,即:

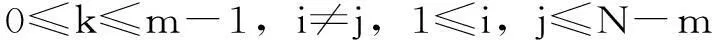
(2)
(3)给定一个阈值r,对每个i值统计到距离d[X(i),X(j)]小于r的数目(称为模板匹配数),并将此数目与距离总数N-m+1做比,比值记作Cim(r),即:

的数目,i≠j},i=1~N-m+1
(3)
(4)求其Cim(r)对所有i的平均值,记作φm(r),即:

(4)
(5)再将维数加1,即对于m+1维矢量重复步骤(1)~(4),得Cim+1(r)和φm+1(r)。
(6)理论上此序列样本熵为:

(5)
当N为有限值时,式(5)表示为:

(6)
样本熵的值的大小显然与m,r,N的取值有关。样本熵算法的核心步骤是计算在一定模式维数m下,2个m维特征向量之间距离的计算及容限范围内距离数目的统计。m取值越大,计算所需要的数据量越大,计算时间越长。r取值的大小关系反映时间序列中细节信息损失的多少,r越大信息缺失越多。样本熵的物理本质就是衡量当维数变化时信号序列中新模式出现的对数条件概率均值,因此理论上样本熵在表征信号序列的不规则性和复杂性方面具有一定意义。Pincus已经研究证明,近似熵的数据点数大致在100~5 000点近似结果较为理想,m=2,r=0.1~0.2SDx(SDx为原始数据的标准差)。因此本文选取r=0.2SDx。
1.2 典型信号的复杂性分析
图1为选取不同频率下的典型信号并使用样本熵方法对其进行复杂性分析,将不同频率的典型信号图像中取1 000个采样点并且根据这些采用数据进行样本熵计算,取m=2,r=0.2SDx。

图1 不同频率下的典型信号
分析表1的数据可以发现在不同频率下的正弦信号的样本熵值呈现一定的规律性,正弦信号的频率越大,样本熵的值越大,表示信号的复杂性越高。三角波与正弦波相类似,但与正弦波和三角波相比,方波的复杂性要小得多,这也体现在样本熵的数值大小上。一般情况下,根据样本熵的算法公式得到的样本熵数值理论上应该在0~1之间,但是若采样的数据值上下波动过大,或者选取的数据长度过长等原因,样本熵的值是可以大于或等于1的。仿真出来的白噪声信号由于其随机性极强,因此它的样本熵的值也远大于1,这表示白噪声信号极其复杂。

表1 各指令信号样本熵值
文献[11]中使用功率谱熵和近似熵的方法也计算过正弦信号及白噪声的复杂性,与本文计算出来的数据相近似。但是对比以上两种方法,样本熵克服了由于矢量自身匹配计入统计量而产生的计算结果偏差,使得数据更为精确。通过对不同频率的典型信号进行复杂性分析,可以看出样本熵方法能够清楚地量化信号的复杂程度,考虑可以使用样本熵方法对AGC指令信号进行复杂性分析。
2AGC信号的复杂性分析
选取西北某电厂660 MW超临界火电机组现场实际运行3天的数据进行分析。由于火电机组AGC是min级别的控制,1天内的数据每间隔1 min采集一次。
选取该厂2014年10月20日~10月22日3天的数据,如图2所示,从图中可以较为直观地看出在不同天的同一时段内的信号指令波动情况较为接近,对其进行复杂性分析,计算结果见表2。再对这3天的AGC指令信号进行局部细分,选取波动较为频繁的区域每间隔15 s采集一个样本点数据进行样本熵值的分析,如图3所示。计算结果见表3。

图2 机组3日的AGC指令信号

表2 3天AGC指令信号样本熵值

图3 较复杂的AGC指令信号
通过图2的信号曲线可以看出,在西北电网省级联络线调度模式的运行条件下,火电机组AGC信号同时呈现高速率大幅度单向变化、高速率中等幅度正反向变化、高速率小幅度频繁波动的特征。而火电机组对于较为平稳的信号跟踪情况显然要比波动频繁的信号要容易得多,而这也可以从样本熵的数值上反映出来。分析表2的数据可以看出在3天内,每天的2:00~4:00,9:00~16:00及21:00~次日凌晨这3段时间内的波动幅度较大,但在其他时间内,AGC指令信号均较为平稳。这说明在相同月份中,电厂每日接收到的AGC指令信号较为相似,与用电侧用户使用情况相关,具有一定的规律性。分析表3的数据可以看出,在波动情况较为频繁的时间段内,它的AGC指令信号的复杂性是比较高的,说明样本熵主要关注的是信号来回波动的频繁程度。
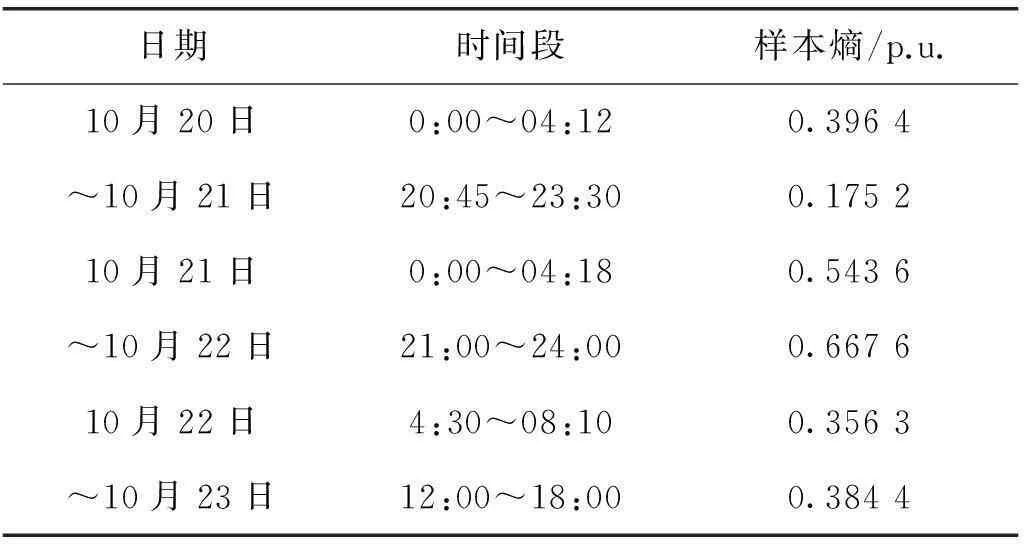
表3 较复杂的AGC指令信号样本熵值
从图2中可以看出,当AGC指令呈现大幅度单向变化时其对应的样本熵值要小于中等幅度正反方向变化所对应的样本熵值。而AGC指令小幅度频繁波动情况下虽然波动频率较大,但是由于变化的幅度小,因此所对应的样本熵值也相对较小。这与现场实际运行情况是一致的,对于火电机组来说大幅度单向变化的信号和小幅度频繁波动的信号对于机组设备的磨损远比中等幅度正反方向变化的信号小得多。对比表2与表3的数据不难看出,表2的样本熵数值较低,这是由于表2的样本熵值反映的是1天内AGC指令信号的复杂性。而表3中的样本熵值比表2的则要大许多,尤其是在中等幅度正反方向的信号中,样本熵值较大。火电机组在跟踪AGC指令信号的时候需要经常性的调峰调频以维持全网内负荷频率稳定。因此这些时间段对于火电机组的整体运行来说是较为困难的。通过曲线变化的剧烈程度也同样可以看出,在升降负荷较为明显的时间段,样本熵数值相差大。
样本熵从AGC指令信号的波动频率及波动的剧烈程度上来对其进行定量分析,能够清楚地反映AGC指令信号的复杂性。而且由于样本熵所需要的采样点较少及具有较强的抗干扰能力,对分析短时间内变化幅度较大的指令信号有一定的优势。
3结论
(1)信号的随机成分越大其复杂性也越高,其中以完全随机的白噪声信号最为复杂,这也反映在对应的样本熵数值上。结果证实了样本熵方法能定量地描述序列的结构特性,能够清楚地区分不同信号的复杂性。
(2)对比使用功率谱熵和近似熵计算出来的复杂性量化值,样本熵方法得出的数值更为精确。
(3)根据对选取的AGC指令进行复杂性分析所得到的数据结果可以看出样本熵能较准确地反映AGC指令信号的复杂性,采样频率越高,得出的数据会更加准确,对分析短时间内变化幅度较大的指令信号有一定的优势。在对不同幅度波形的分析中所得到的样本熵值,与现场运行实际情况相吻合。
(4)本文使用的样本熵分析方法可以作为一种可行的方案用来区分发电任务的难易程度。在一定程度上完善了电网考核标准“两个细则”中的部分缺陷。使发电侧在考虑“两个细则”等相关的考核指标的同时,还可以通过定量化计算来分析其接收到的AGC调度指令信号的难易程度,从而向供电侧要求一定额外的补偿或奖励。兼顾了火电机组的特性,使其能够更加安全、稳定、高效的运行。
参考文献:
[1]邹斌,许卫洪,丁峰. 一种新的AGC机组绩效考评方法[J]. 电力系统自动化,2005,29(11):23-28.
[2]李端超,江山立,陈家庚,等. AGC机组调节效能定量评估与补偿方式研究[J]. 电网技术,2001,25(8):15-19.
[3]赵旋宇,李鹏,汪皓,等. 新型控制性能评价方法及相应的自动发电控制模式[J]. 中国电机工程学报,2010,30(16):93-97.
[4]钱学森. 一个科学新领域——开放的复杂巨系统及其方法论[J]. 城市发展研究,2005,12(5):1-8.
[5]宋学峰. 复杂性、复杂系统与复杂性科学[J]. 中国科学基金,2003,17(5):262-269.
[6]Pincus S M. Approximate entropy as a measure of system complexity [J]. Proceedings of the National Academy of Sciences,1991,88(6):2297-2301.
[7]Richman J S,Moorman J R. Physiological time-series analysis using approximate entropy and sample entropy [J]. American Journal of Physiology-Heart and Circulatory Physiology,2000,278(6):H2039-H2049.
[8]和卫星,陈晓平,邵珺婷. 基于样本熵的睡眠脑电分期[J]. 江苏大学学报(自然科学版),2009,30(5):501-504.
[9]白冬梅,邱天爽,李小兵. 样本熵及在脑电癫痫检测中的应用[J]. 生物医学工程学杂志,2007,24(1):200-205.
[10]向郑涛,陈宇峰. 基于多尺度熵的交通流复杂性分析[J]. 物理学报,2014,(3):473-481.
[11]金宁德,董芳,赵舒. 气液两相流电导波动信号复杂性测度分析及其流型表征[J]. 物理学报,2007,56(2):720-729.
[12]王瑞琪,刘吉臻,高萌,等. 火电机组AGC指令特性分析[J]. 华北电力大学学报,2013,40(5):84-89.
[13]郝祖龙,刘吉臻,常太华. 基于小波变换的热工信号多尺度相关性分析[J]. 中国电机工程学报,2010,30(14):109-114.
[14]郝祖龙,陈磊,常太华. 典型工况火焰强度信号的复杂性分析[J]. 电力科学与工程,2006,(4):28 - 31.
[15]张永军,陈波. 浙江电网火电机组AGC运行状况及性能考核分析[J]. 浙江电力,2010,(3):35-39.
[16]司瑞才. AGC负荷自动分配的研究[D]. 北京:华北电力大学, 2011.
[17]王瑞琪.火电机组AGC指令及负荷响应曲线特征分析[D].北京:华北电力大学,2014.
[18]言茂松,邹斌. 概率学的AGC先验定价和后验考核新方法[J]. 电力系统自动化,2003,27(2):1-6.
[19]王娟娟,吕泉,李卫东,等. 电力市场环境下需求侧AGC成本的分摊策略[J]. 电力自动化设备,2012,32(6):31-35.
[20] 郝祖龙,刘吉臻,常太华,等. 锅炉燃烧扰动相关信号的提取[J]. 热力发电,2010,39(8):18-22.
Analysis of the AGC Instruction Complexity Based on Sample Entropy
Zhang Shukai1, Liu Xinping1,Zhang Ruifeng2(1. School of Control and Computer Engineering, North China Electric Power University, Baoding071003, China;2. Guizhou Electric Power Test and Research Institute, Guiyang 550002, China)


