Complexity and Intelligence:From Church-Turning Thesis to AlphaGo Thesis and Beyonds(2)

WANG Fei-Yue

1.Research Center of Military Computational Experiments and Parallel Systems Technology,The National University of Defense Technology,Changsha Hunan 410073,China 2.The State Key Laboratory of Management and Control for Complex Systems,Institute of Automation,Chinese Academy of Sciences,Beijing 100190,China

Abstract AlphaGo’s victory over a top human professional player offers a new way of thinking on engineering solution for complexity and intelligence,called “The Extended AlphaGo Thesis” here.This might have a significant impact on the command and control of future intelligent military and smart wars,and has verified technically the soundness of concept and method of parallel systems based on virtual-real interaction as an effective approach for a new military system of systems.

Key words AlphaGo,complexity,intelligence,intelligent military,smart wars,parallel military,parallel command and control

2 基于信息的复杂性及其分析

何谓复杂性？Kolmogorow复杂性或算法熵是关于现代复杂性研究的开始.如何在智能系统研究中引入复杂性分析,是我30年所面临的问题.我在McNaughton和Saridis的帮助下,曾写过3份研究报告[18−20],其中第1份基本被否定,但第3份引入基于信息的复杂性概念,主要受S.F.Traub等的工作影响[21−26],自己还算满足.后由于其他工作的影响,这项研究没有再深入,所以一直没有发表,许多年后,连研究工作报告也不知在何处.万幸的是,我的博士生在我从美国带回的材料中,竟然找到了这份近30年前写的研究报告[20].在此,我摘录其中的1节于此,让大家了解自己当时从事复杂性研究的思路,或许对关于智能与复杂性的更进一步研究有所帮助.

Complexity Analysis in Intelligent Machines

In this section we address the issue of complexity analysis in Intelligent Machines.The motivation of performing complexity analysis for an Intelligent Machine is to determine the intrinsic limit and ability on which tasks can be accomplished by that Machine.

The performance of task processing of Intelligent Machines will be measured by precision or reliability.To include the reliability as the measure of performance is based on the consideration that for many tasks,especially the higher level tasks,in an Intelligent Machine,their solutions(i.e.,ways to accomplish tasks)are not unique and are not defined in the conventional normed spaces(e.g.,the normed linear space G in information-based complexity),therefore the terms“error”and then“precision” are not well defined for those tasks.Instead,the performance of those tasks are usually described by the degree of satisfaction of certain specifications(McInroy and Saridis,1989).Reliability can then be used as a probabilistic measure of assurance of performance.Like the precision of a task processing,its reliability can be computed off-line or estimated by on-line observation.

The two central questions of complexity analysis for an Intelligent Machine are,

·What is the minimal cost to accomplish a task by the Machine for a given level of precision or reliability?

·What is the maximal precision or reliability accomplished for a task by the Machine with a specified level of cost?

It is very important to point out that here we discuss the complexity within the context of a specific Machine,not with respect to all Machines.In other words,we talk about the complexity of a task processing by an arbitrary single Machine,which is a machine-dependent quantity,not the complexity of a task processing by all Machines,which is a machine-independent quantity.The reason for this is simple:we want to find a way to measure the ability and limit of a specific Intelligent Machine,not that of all Intelligent Machines.The later is too complicated to be accomplished at the current stage.

Following the formulation of informationbased complexity,we will formalize the problem of complexity analysis for Intelligent Machines.Since we just investigate the complexity of task processing of a specific Machine,unlike in the information-based complexity where almost all possible information operators and algorithms are assumed to be available,we have to assume that the specific Machine has only finite number of information operators and algorithms for its task processing.

A.Complexity of Machine Precision:The formulation ofcomplexity of machine preci-sionis a triple

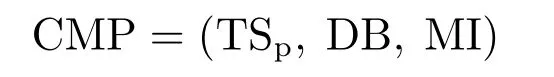
where

1.TSp=(T,D,E,ε)istask specification:

·T:a finite set oftasks.An element f from T is called a task.

·D:T→DB×MI is thedecision mapping.D(f)=(ND,φD)indicates a decision to processing task f with information operator NDand algorithmφD.

· E:D(T)→R+is theerror function.E(D(f))defines the error of the decision D at task f.R+=[0,+∞).

·ε∈R+is the specification ofprecision:D is called anε-approximate decisionat f iffE(D(f))≤ε.The error of a decision D can be defined in different settings(e.g.,the worst,average,and probabilistic cases).For simplicity,we consider only worst case setting,therefore,theworst case errorof D is defined by

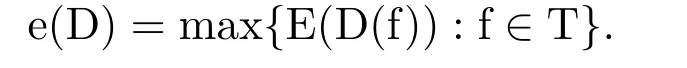
D is called anε-approximate decisioniffe(D)≤ε.

2.DB=(H,Λ,N1,...,Ns)isdatabase specification:

·H:a set of measurements of the database.

·Λ:a finite set of primitiveinformation operationsof the database.An element L from Λ is a mapping L:T→H.L(f)represents the information about f through the computation of the form L(f).The cost of each information operation is assumed to be a constantcDB(cDBprimitive operations).

·Ni:T→K is aninformation operator.Ni(f)specifies the information about task f obtained by Ni.K={[L1(f),...,Lm(f)]:f∈T,Li∈Λ,m＞0}is the set of all finite sequences of information operations.

3.MI=(Ω,φ1,...,φt)isalgorithm specification:

·Ω:a set of primitivecomputational operations.The cost of each computation operation is assumed to be a constantcMI(cMIprimitive operations).

·φi: N1(T)∪...∪Ns(T)→G is analgorithm,

where G is the set of task solutions.An algorithm combines the known information N(f)and produces an approximate solution for a task,using computational operations in Ω.

Now we can define theε-complexity of machine precision. The total cost of decision D(f)=(ND,φD)at task f is given by

where cost(ND,f)is thedatabase costof computing ND(f)and cost(φD,ND(f))is thedecision costof computingφ(ND(f)).The cost here is defined in terms of the number ofprimitive operationsperformed.The primitive operations include the addition,multiplication,etc.The cost of computation of decision D in the worst case setting is given by

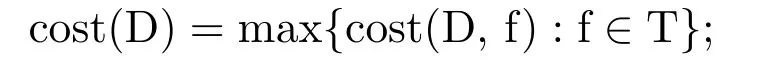
Theε-complexity of machine precisionis then defined as the minimal cost among all decisions with error at mostε,

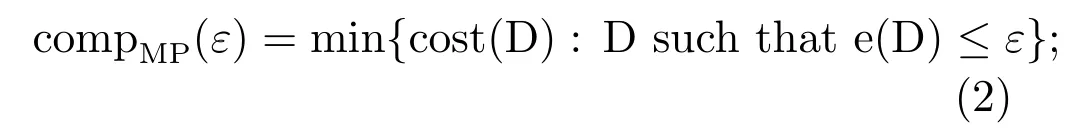
compMP(ε)is the measure of difficulty of processing tasks with the given precisionεby an Intelligent Machine.A task cannot be accomplished with precisionεif the operational resource assigned is less than compMP(ε).Tasks that cannot be achieved because limitations dictate that the requisite operational resources cannot be granted by the Machine are said to beintractableby the Machine.

C-precisionis defined as the minimal error among all decisions which accomplish the tasks with cost at mostC,

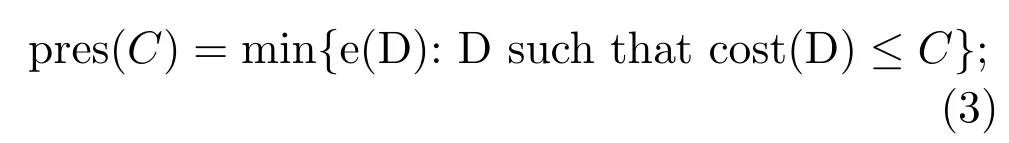
pres(C)is the upper bound of precision of processing tasks with the given operational resourceC.Precision higher than pres(C)cannot be achieved with the resource bounded byC.

B.Complexity of Machine Reliability:The formulation ofcomplexity of machine reliabilityis a triple

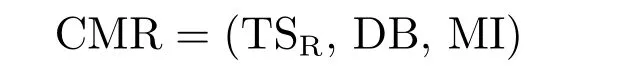
where

1.TSR=(T,M,S,D,δ)istask specification:

·T:a finite set oftasks.An element f from T is called a task.

·M:a finite set ofspecifications.

·S:T→M is thespecification mapping.S(f)represents the specifications to be met by task f.

·D:T→DB×MI is thedecision mapping.D(f)=(ND,φD)indicates a decision to processing task f with information operator NDand algorithmφD.

·δ∈[0,1]is the specification ofreliability:D is

called anδ-reliable decisionat f iff Prob[S(f)is true|D(f)]≥δ.Theworst case reliabilityof a decision D is defined by

r(D)=max{Prob[S(f)is true|D(f)]:f∈T};

D is called anδ-reliable decisioniff r(D)≥δ.

2.DB=(H,Λ,N1,...,Ns)is the same database specification as in the formulation of complexity of machine precision.

3.MI=(Ω,φ1,...,φt)is the same algorithm specification as in the formulation of complexity of machine precision.

Now we can define theδ-complexity of machine reliability.As for complexity of machine precision,the total cost of decision D(f)=(ND,φD)at task f is given by

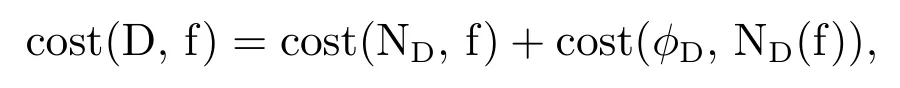
and the cost of computation of decision D in the worst case setting is given by

Theδ-complexity of machine reliabilityis then defined as the minimal cost among all decisions with reliability at leastδ,

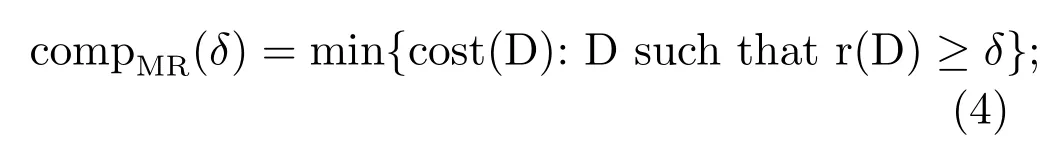
compMR(δ)is the measure of difficulty of processing tasks with the given reliabilityδby an Intelligent Machine.A task with the specified reliabilityδis intractable if the operational resource assigned is less than compMR(δ).

C-reliabilityis defined as the maximum reliability among all decisions which accomplish the tasks with cost at mostC,

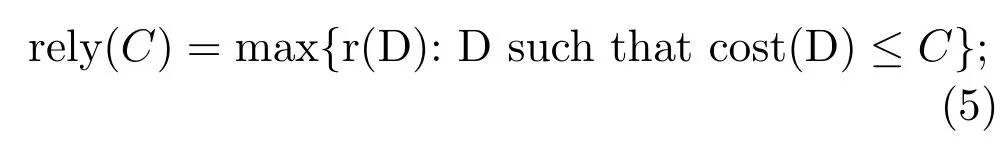
rely(C)is the upper bound of reliability of processing tasks with the given operational resourceC. Reliability higher than rely(C)cannot be achieved with the resource bounded byC.

The main difference between the informationbased complexity and the machine complexities is that,in information-based complexity,the complexity is computed on the convention that the same information operator and algorithm will be used for all the problems,however,in both machine precision complexity and machine reliability complexity,the complexity is calculated on the assumption that the different information operator and algorithm are allowed to be used for different tasks.The decision to find suitable information operator and algorithm for a task is specified by the decision mapping D.This is because the facts that only a finite number of information operators and algorithms is available for any kind of task processing by any specific Intelligent Machine and that a Machine is capable of obtaining different information and applying different controls for different tasks.

The complexity formulation of machine precision or reliability can be applied in complexity analysis of any task processing units in an Intelligent Machine.Depending on the connection confi guration of task processing units is sequential or parallel,the resulting complexity will be the maximum of complexities of task processing units or the sum of complexities of task processing units.For example,in Petri net model of the Coordination Level of an Intelligent Machine(Wang and Saridis,1990),each of the transitions in a Petri net transducer can be considered as a task processing unit,and therefore we can use the above complexity formulations in their complexity analysis.When complexities of information operators and algorithms(cost(ND,f)and cost(φD,ND(f)))are unknown and uncertainty but can be observed from the task execution,they can be used as the performance indices in the on-line learning algorithm for decision making in Petri net transducer.

By the same arguments made for informationbased complexity,equation(5)indicates that to processing tasks by a task unit of Machine with the given operational resource and the specified precision(or reliability),higher intelligent algorithms have to be used for small size databases and lower intelligent algorithms have to be used for large size databases.This observation verifies the principle of IPDI of Intelligent Machines for any specific task processing unit.Since complexity is additive,we can reach the conclusion that the principle holds for any subsystem of an Intelligent Machine.

（未完待续）