数学课堂教学中教师的引导策略探究

赵绪昌

叶圣陶先生说：“教师之教，不在于全盘讲授，而在于相机引导. ”在以学生发展为本的课堂里，特别强调尊重学生的主体地位和独立思考，因而对教师的引导提出了更高的要求. 引导，《现代汉语词典》中与教学语境更为贴切的解释是“指引；诱导”. “引”的含义是指引，指引须是有目标、有方向的，但指引可能只是提醒或提示；“导”的含义是诱导，使用一定的教学方法或手段深化学生的数学理解，激发学生的数学思考. 教学中的“引导”，其本意是“以明确的教学目标为指引，通过有效的教学方法或手段深化理解，激发思考”. 在数学教学过程中，教师应做到导之有趣，导之有时，导之有法，导之有度，促进学生思维参与，提高课堂教学效益. 下面举例说明.

一、导之有趣 使学生想学

“导之有趣”是指在数学课堂教学中要构建有趣的课堂. 心理学研究表明：有趣的课堂，往往会给学生带来新异、亲切的感受，不仅能使学生迅速地从抑制到兴奋，而且还会使学生把学习当作一种自我需要，自然地进入学习新知的情境. 引导关键在于激活学生的“动情点”，将学生置于“心求通而未达，口欲言而不能”的心理状态. 教学过程中教师可借助游戏、猜谜、讲故事、设置悬念等形式引导激发学生的学习兴趣，变学生的“要我学”为“我要学”.

案例1 “弧度制”的教学片段

铃声一响，全班学生和听课的教师正襟而坐，静静等待任课教师开始上课. 这时，只见教室门被推开，上课教师手拿一面折扇，不慌不忙地走上讲台，悠然而立，“唰”的一声打开折扇慢悠悠地摇动起来. 学生及听课教师如坠雾里，满眼诧异：此时天气正冷，教师这是唱的哪一出戏呢？

正在大家莫名其妙之时，教师将扇子一举说：“同学们，请看这是什么图形啊？”学生大声回答：“扇形！”教师又问：“你会做扇形吗？”学生：“将圆剪出一部分. ”教师又问：“如果要使做出的折扇更好看，应该怎么剪呢？”学生纷纷议论，有的迫不及待地开始动手实验，有的却无从下手. 此时教师又说话了：“谁做的扇形好看，我们便把它叫作黄金扇！”听到此话，有的学生顿时惊醒：“黄金分割率. ”教师会心一笑：“对，只要让你剪出的扇形面积和剩余部分的面积比值符合黄金比例即可，那么怎么求出扇形的面积，以及剪出扇形的圆心角应该是多少呢？学完本节课，希望同学们能够轻松地完成该任务. ”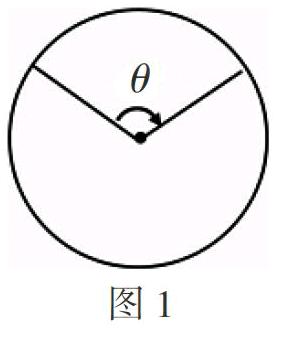

至此，听课教师才恍然大悟，原来如此！而学生的学习兴趣也被充分调动起来了，然后便开始了“弧度制”的学习. 因为学习气氛热烈，效率大大提高，学生很轻松地掌握了弧度制的概念、弧长和扇形的面积公式. 离下课还有五分钟时，教师又提出了新授课前的问题：“哪位同学能给出黄金扇形的圆心角的求法，请上讲台来展示一下. ”话音未落，一名学生便走上讲台开始讲解：如图1，假如设计纸扇的圆心角为θ，则剩余部分的圆心角为2π-θ. 而折扇面积S1与剩余面积S2的比值为黄金比例值0.618.

由扇形面积公式可得==0.618，则θ=0. 618（2π-θ），所以θ≈0.764π≈140°.

即只要纸扇的圆心角大约为140°时，该纸扇符合黄金比例，所以最好看.

【教学随想】 本节课教师以满腔的热忱感染着学生，以高超的教学艺术引领着学生，其独特的教学风格和炉火纯青的教学艺术在本节课上得到了充分的体现，课堂设计情境前后照应，整堂课精彩纷呈，让人精神愉悦、回味无穷，学生分析思路清晰，公式应用准确. 这真是：一把折扇贯始终，角度弧度在其中. 奇思妙想巧点拨，学以致用标达成. 这样，通过创设情境，学生的兴趣被调动了，学生的思维也逐步推向深入.

二、导之有时 使学生能学

“不愤不启，不悱不发”是说教师要在学生思而未得感到苦恼时帮助开启；要在学生思而有所得，但却不能准确表达时予以疏导. 课堂教学中的引导要讲究灵活，教师要善于创设“愤、悱”的情境，要及时抓住新旧知识的连接点的信息作为引导的“话题”，于思维阻碍时启发提升、于思维定式时启发创新、于偏离目标时引导拨正、于动态生成时因势利导、于方法多样时沟通优化、于知识整合时引导沟通、于融会贯通时沟通拓展，灵活地组织教学，使学生的数学学习活动真正是一个生动活泼、主动的和富有个性的过程.

案例2 “抛物线及其标准方程”中的概念教学片段

旧教材在椭圆与双曲线中要学习第二定义，我们知道：按第二定义，当01时，轨迹是双曲线；那么e=1时，轨迹又是什么呢？所以抛物线概念的引出不必花太多工夫，可以开门见山地直奔主题. 但是新教材删除了第二定义，所以引出抛物线的概念就变得相当困难，有的教师把握不准《课程标准》和《学科指导意见》，就或多或少地增加了第二定义的内容，抛物线的教学仍然与旧教材的教法一样；有的教师为了能够上好抛物线，也增加了第二定义的教学. 这种做法“方便”了教学，却加重了学生的负担. 那么到底应该怎样进行教学呢？因为学生已经具备椭圆、双曲线和初中层面抛物线的知识，我们应从学生已有的知识引导出新概念.

问题1：若点P（x，y）满足+=6，则点P的轨迹是 .

生1利用平方化简，但没有做出来.

师：该同学利用平方化简，肯定可以得到答案，只是还需要一些时间，相信他一定能成功！

生2：上面式子表示两点距离之和，根据椭圆定义可知，P点轨迹是椭圆.

众生：是的.

问题2：若点P（x，y）满足-=6，则P点的轨迹是 .

众生：双曲线.

师：是双曲线吗？

生3：应该是双曲线的上半支.

由于问题1的解决对问题2有着提示和启发作用，所以问题2几乎所有学生都不再化简了，自然地联想到利用定义的解法，于是教师顺势抛出问题3.

问题3：若点P（x，y）满足-|y+2|=0，则P点的轨迹是 .

众生：从条件的含义看，似乎不是椭圆，也不像双曲线，不太清楚.

师：到底轨迹是什么？生1解问题1的方法会给我们很好的启示.

生：因为它的方程是y=，它是我们初中已经学过的抛物线.

师：若把条件中的“2”改为其他数字（非零），结果如何？

众生：轨迹仍然是抛物线，只是方程中的数字不同而已.

师：那么条件所表示的几何意义又是什么呢？

生4：原方程即=|y+2|，左端表示点P（x，y）到点（0，2）的距离，右端肯定不是两点的距离，但它是点P（x，y）到直线y=-2的距离，等式表示两个距离相等.

师：从问题3的分析中我们可以看出，满足这种条件的轨迹都是抛物线. 于是我们抛弃这些具体的位置和数据外壳，得出抛物线的定义. 哪位同学能根据上面的等式，说出抛物线的定义？

生5：到定点的距离和到定直线的距离相等的点的轨迹是抛物线.

师：不太准确，应该添上“平面内”三个 字，完整的定义请同学们看课本. 我们再用动画来演示一下这个定义下的轨迹.

【教学随想】 案例中，教师从学生已有知识出发，由易到难设计了三个问题，让学生在问题解决的过程中对比发现，逆推出抛物线的定义，再结合多媒体动画的演示，给学生留下了深刻的印象. 事实上，在探讨中也让学生领悟了一些解析几何的思想方法，如根据定义判断轨迹、运算化简求轨迹等. 可见，正是这匠心独运的引导，有效激活了学生的思维，成就了一段师生、生生之间的思维对话.

三、导之有法 使学生会学

“导之有法”是指教师的引导要有方法，通过有效引导使学生获得成功. 心理学家认为：成功感是学生完成某项学习任务后产生的自我满足和积极而愉快的情绪状态. 这种成功的喜悦转化为进一步学习的强大动力，再次激发学生的求知欲. “没有动力不能学，没有方法不会学”. 于教学重点、教学难点、提升能力等处引导学生充分展示学习的潜在能力，让每个学生享受“成功之乐”，使学生会学.

案例3 “等比数列的前n项和”的教学片段

求等比数列{an}的前n项和.

Sn=a1+a2+…+an（1）时，设公比为q，由通项公式，得Sn=a1+a1q+a1q2+…+a1qn-1.（2）

待学生阅读课本后.

师：课本上是如何求前n项和公式的？同学们概括一下.

生1：用 q乘（2）式两边，与（2）式有很多相同项的等式qSn=a1q+a1q2+…+a1qn-1+a1qn. （3）

（2）（3）两式相减就可得到前n项和公式.

师：噢！用q乘（2）式后两边产生了与（2）式有很多相同项的（3）式，为何要两式相减？

生2：因为两式相减可把相同的项消去，达到化简的目的.

师：共有多少对相同的项？

生3：噢——共有n-1对.

观察式（1）（5），都含有n-1对相同的项，因此，可用减法消元：（1）-（5）得（1-q）Sn=a1-anq，即 Sn=（q≠1），得到（4）式.

师：用减法进行消元时，你们看看有什么特点，怎样来概括这种方法？

生7：相同的项在两个式子中的排列是错位的，消元做减法，故称为“错位相减法”.

师：好的. “错位相减法”不仅能求等比数列的前项和，而且，它的思想方法还可以解决其他的问题，请同学们回想一下，等差数列的通项公式是如何推导出来的？

生8：是通过观察、概括的方法得到的，还没有证明.

师：是的，还需要待以后用数学归纳法来严格证明，那么，我们设等差数列{an}的首项为a1，公差为d，同学们试一试，可不可以用“错位相减法”求an？

师：太漂亮了，大家给点掌声！我们用“错位相减法”把悬而未证的等差数列的通项公式给出了证明，使我们应用公式更加踏实！

【教学随想】 “等比数列的前n项和”的教学，一般来说，教师按照课本的方式，照本宣科，给出推导，至于为什么这样推导，它的目的是什么，还有没有其他方式推导，这些推导方式的本质是什么部分教师没有思考，更没有引导学生去思考、讨论、解答，致使学生对“等比数列的前n项和”记住公式直接应用，知其然而不知其所以然. 案例中，教师从教材中“求等比数列的前n项和”的方法出发，引导学生探索了“求等比数列的前n项和”的加减消元法和代入消元法，分析两种方法的实质是“错位相减法”，很自然地用“错位相减法”证明了等差数列的通项公式. 这样变换思维角度，打开思维通道，渗透数学思想和方法，既使学生享受了学习的快乐，又使学生掌握了学习方法，可谓一举两得！

四、导之有度 使学生多学

“导之有度”是指教师要把握“导”的程度，凡是学生自己能够解决的问题，教师决不替代，学生自己能够思考的问题，教师决不暗示，这就需要教师就“该追问则追问，该启发则启发”的引导艺术进行深入的研究. 课堂教学中教师掌握了引导的“度”，就能让学生有更多的“自主探索”时间，从而使学生多学.

案例4 设点O是△ABC内部一点，且满足+2+=0，则△AOB与△AOC的面积之比为 . （答案：1∶2）

批阅作业时，教师发现该题的出错率极高，于是在随后的课上对该题做了详细的讲解. 讲解完之后，照惯例给了学生几分钟自由讨论和订正整理时间. 一个学生提出的疑问吸引了所有人的注意.

生1：本题的面积之比和条件“+2+=0”中“”，“”的系数之比相同，这是巧合，还是必然？

教师一时不知如何回答，便灵机一动，对该题的条件稍做变化，给出了如下变式.

变式：已知点O在△ABC的内部，且有+3+=0，则△AOB与△AOC的面积之比为 .

师：到底是巧合，还是必然？请同学们完成变式题后自己去判断.

很快，学生得出答案是1∶3，这和题目条件中“”，“”的系数之比也完全相同. 规律再次出现，课堂气氛悄然升温，几乎所有学生都觉得这其中一定存在相应的结论. 凭直觉，教师也觉得这绝不会是一个巧合，其背后一定隐藏着必然的规律. 可以肯定地说，学生的疑问正是一个难能可贵的生成性资源.

师：看来我们今天会有意外的收获了，请同学们发挥想象，对结论进行合理猜想.

教师引导学生对猜想5进行证明是正确的.

【教学随想】 案例中，教师没有对数学问题浅尝辄止，而是通过适时适度引导，从最初学生的质疑，到三个猜想的得出和证明，再到“点O是△ABC外部一点”，最后拓展到更为一般的结论，不仅学生的探究能力得到了提高，而且同时学习了猜想与归纳、推广与拓展的方法，帮助学生形成了“功能良好的数学认知结构”，使学生达到“解一题，会一类”的目的，避免了数学教学中的“题海”战术，真正达到了“减负增效”的效果.

总之，在新课程理念下的数学课堂教学既要注重学生的自主探索，又要重视教师的有效引导，当学生的自主探索有障碍时，教师就应发挥主导的作用，通过有效引导，降低教学难点，节约教学时间，提高教学效益，巩固教学成果. 数学课堂教学应该追求自主探索与有效引导的和谐统一.