集材区选址与能力配置的集成优化问题

潘静静，胡志华

(1.福建农林大学交通与土木工程学院， 福建福州350002； 2.上海海事大学物流研究中心， 上海201306)



集材区选址与能力配置的集成优化问题

潘静静1，胡志华2

(1.福建农林大学交通与土木工程学院， 福建福州350002； 2.上海海事大学物流研究中心， 上海201306)

摘要：为了解决木材供给的集中性和季节性，与需求的分散性和持续性之间的矛盾，针对集材区的选址与能力配置问题，以最小化木材物流网络总成本为目标，建立混合整数规划模型，使用Gurobi工具求解得到集材区选址与能力配置结果。考虑调整模型参数，设计4组实验，通过算例验证模型的可行性和有效性，基于实验结果，分析模型参数变化对木材物流网络优化结果的影响。

关键词：物流管理；木材物流；选址；混合整数规划；物流网络

0引言

木材物流网络是指由木材采伐、储存和加工节点，以及木材运输线路两种基本元素构成的网络结构，包括木材从伐区、到集材区、再到造纸厂等工厂的整个过程[1]。对木材物流网络的合理规划，有利于降低木材物流成本，减少木材流通过程中产生的污染，保护林业生态环境。木材物流网络优化旨在解决木材供给的集中性和季节性，与需求的分散性和持续性之间的矛盾。木材物流网络的构造和设计包括设施选址和流量分配等问题[1]。一般设施选址是从有限个备选设施中找出能够使物流活动的总运距或总成本最小的设施集合[2-3]。

在国外，木材物流和木材加工供应链是林业物流研究的重心[4]。针对一个双层木材供应链系统，Chauhan等[5]研究木材物流中采伐、加工和运输决策的综合优化问题。Frisk等[6]提出相应于不同伐区的木材供应商之间进行协作的方法，通过共同配送降低运输成本。在木材供应链研究方面，Carlsson等[7]从战略、战术和运作三个层次对木材供应链规划模型进行综述。在国内，主要通过木材物流中心选址、木材运输和木材库存优化等问题，对林产品物流过程进行有效的控制。为了确定木材物流网络的物流中心数量、位置以及运输方案，陈诚等[8]建立木材物流网络优化的混合整数规划模型。基于地理信息系统(GIS)，邱荣祖等[9]建立木材物流中心选址优化决策模型并采用遗传算法求解。基于GIS和遥感技术，张淑芬等[10]研究伐区木材运输路线优化问题。刘俊[11]系统地研究了造纸木材供应链的优化与仿真系统。针对木材物流运作造成的林木资源浪费和生态环境破坏，胡婷婷[12]阐述了林业绿色供应链的理论体系，对木材采购和库存优化等问题进行研究。

已有的研究普遍针对木材物流网络中的节点选址与运输线路规划建立模型，而较少研究将节点能力配置问题体现在优化模型中。Chauhan等[5]在木材网络优化中主要研究多种木材混合运输问题，未对木材进行分类运输，缺乏对需材企业的生产实际需要的考虑。Melo等[2]研究木材物流网络中节点选址问题，未对节点的能力配置问题进行考虑。Frisk等[6]研究木材物流网络中运输问题，但未涉及网络中节点选址及能力配置问题。基于上述研究，以木材物流网络的运输成本及节点成本最小化为目标，本文建立一个混合整数规划模型，从集材区选址和配置节点能力两个角度优化木材物流网络。

1问题描述

木材物流网络中，集材区是对木材进行转运、暂存、装卸和加工的场所。木材采伐与运输受到气候因素制约，例如在雨季和融雪期，伐区林道承载力下降，木材的搬运、装卸和运输难度增加，使得木材的供给存在不确定性[13]。在伐区砍伐的木材运至集材区，在集材区保有适量的木材库存，可以消除木材供给不确定性引起的木材短缺，保证木材物流网络的通畅性。另外，随着产品生命周期缩短，以木材为主要原材料的造纸厂等企业越来越倾向于按订单生产，要求原材料供应商根据其生产计划实行准时制送货。对供应商来说，既要及时供应又要避免集材区的库存积压。因此，集材区作为一个调节木材运输与库存平衡的节点，对其进行合理选址与能力配置，是木材物流网络优化的重要内容。

本文研究的木材物流网络包括以下节点：以木屑为主要原材料的造纸厂，为造纸厂提供原材料的伐区，以及调节造纸厂和伐区间的木材运输和库存平衡的集材区。伐区集合I通过i索引；集材区集合J通过j索引；造纸厂所需木材的类型集合为K，通过k索引。为了降低木屑的库存成本，造纸厂要求木屑供应商执行JIT(Just-In-Time)策略进行送货。在JIT供给中，供应商采用两种木屑供给方案：一是在伐区对立木进行砍伐，使用e台伐区作业联合机[14](实现打枝、剥皮、削屑等功能的林业机械，以下简称“联合机”)，在伐区就地将木材加工成木屑运往造纸厂；二是在伐区对立木进行砍伐，伐倒后的木材运至集材区暂存，在造纸厂需要时将木材加工成木屑，再将木屑运往造纸厂。本文考虑的木材物流运作流程如图1所示，木材物流网络设计与优化所涉及的决策问题包括集材区的数量选择、选址和生产能力配置；伐区对集材区的分配关系；伐区的联合机的数量配置。笔者以木材物流网络的总成本最小化为目标，优化集材区选址、伐区和集材区能力配置。

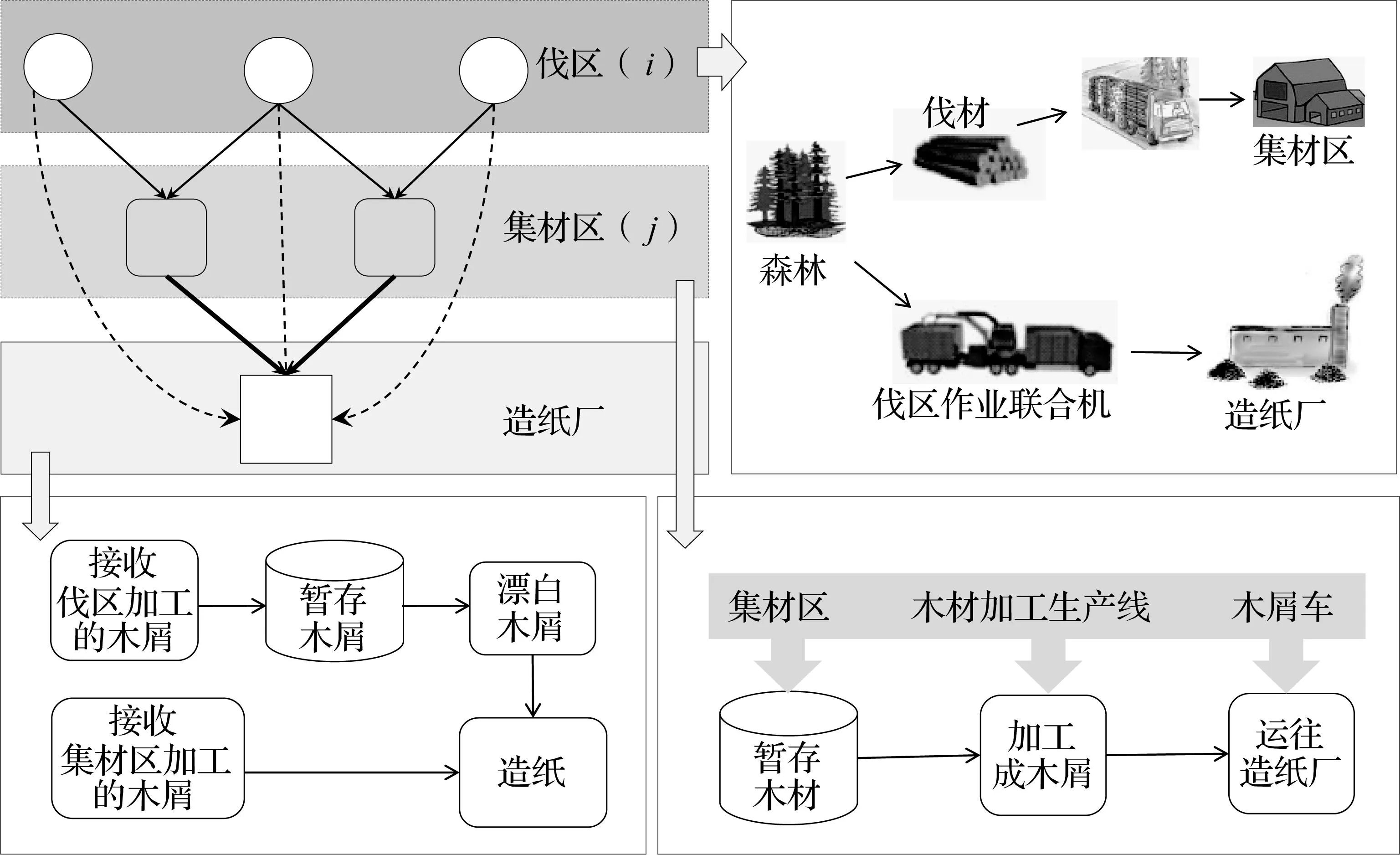
图1　木材物流运作流程

2模型

2.1　模型参数定义

集材区固定成本通过Bj表示，包括建设成本、折旧费和维护费用等成本；Cijk表示木材从伐区运往集材区的单位物流成本，即每立方米第k种木材从伐区i运往集材区j的成本，包括采伐和运输成本；Dik表示木材从伐区运往造纸厂的单位物流成本，即每立方米第k种木材从伐区i运往造纸厂的成本，包括采伐、联合机作业成本；Fj表示在集材区配置一条木材加工生产线所需的固定成本；Ge表示在伐区配置e台伐区联合机的固定成本；Hjk表示木材从集材区运往造纸厂的单位物流成本，即每立方米第k种木材从集材区j运往造纸厂的运输费用；Qj表示集材区的每条生产线的生产能力，即在第j个集材区配备一条生产线至多能够处理Qj立方米木材；Se表示e台联合机的生产能力，即在伐区配置e台联合机至多能够处理Se立方米木材；Tik表示伐区的供给能力，即在采伐计划限制下，伐区i至多能够供给Tik立方米第k种木材；Ak表示剥皮的木材加工成木屑后重量损失的比率，则(1-Ak)表示木材加工成木屑后相对于加工前重量的比率；Bk表示木材剥皮前和剥皮后木材重量的比率；Cpenalty是一个足够大的数，表示木材供给不足导致造纸厂原材料短缺的单位惩罚成本；Nk是造纸厂对第k种木材的需求量，假定为一个常数。

定义五组决策变量。第k种木材从伐区i运往造纸厂的数量用uik表示；第k种木材从伐区i运往集材区j的数量用xijk表示；vjk表示第k种木材从集材区j运往造纸厂的数量；yj是0/1变量，当集材区j被选中时取值为1时，否则为0；wj表示在集材区j配置木材加工生产线的数量；ze是0/1变量，表示当伐区配置e台伐区联合机时取值为1，否则为0。

2.2　建立模型

基于上述参数和决策变量建立木材物流网络优化模型。

min

f=f1+f2+f3+f4+f5+f6+f7,

(1)

where

f1=∑ijkCijkxijk,

(2)

f2=∑ikDikuik,

(3)

f3=∑jkHjkvjk,

(4)

f4=∑jBjyj

(5)

f5=∑jFjwj

(6)

f6=∑eGeze,

(7)

f7=Cpenalty∑k[Nk-(∑jvjk+∑iuik)],

(8)

s.t.

uik+∑jxijk≤Tik,∀i,k,

(9)

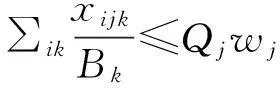
(10)

wj≤Rmaxyj,∀j,

(11)

(1-Ak)∑ixijk=vjk,∀j,k,

(12)

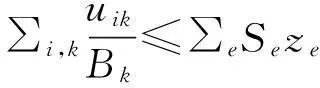
(13)

∑eze≤1,

(14)

∑jvjk+∑iuik≤Nk,∀k,

(15)

xijk,uik,vjk,wj≥0,∀i,j,k,

(16)

wj∈Z,∀j,

(17)

yj∈{0,1},∀j,

(18)

ze∈{0,1},∀e,

(19)

式(1)为木材物流网络的总成本，集材区选址与能力配置以使木材物流网络总成本最小为目标;式(2)~式(4)分别表示木材从伐区运往集材区、从伐区直接运往造纸厂、从集材区运往造纸厂的物流成本;式(5)表示集材区的固定成本;式(6)表示生产线的固定成本;式(7)表示伐区联合机的固定成本;式(8)表示木材供给不足导致造纸厂原材料短缺的惩罚成本;式(9)为伐区的流量平衡约束，即从伐区送往造纸厂和集材区的木材量不能超过伐区的最大供应量;式(10)表示从伐区送往集材区的木材量不超出生产线的生产能力;式(11)只在集材区配置生产线，其中Rmax是一个足够大的数;式(12)是集材区的木材经过加工后的量等于从集材区送往造纸厂的量;式(13)表示从伐区送往造纸厂的木材量不超出联合机的生产能力;式(14)表示至多只能选择一种联合机的配置；式(15)表示造纸厂的需求必须被满足；式(16)为非负约束;式(17)为完整性约束;式(18)和(19)表示yj和ze是0/1变量。

3实验及分析

在本文实验中，假定伐区供给和造纸厂需求的木材量已知；森林伐区位置坐标(x,y)和相应位置的供给能力Tik由系统随机生成；伐区到集材区、集材区到造纸厂及伐区到造纸厂的物流成本主要考虑运输成本，且不考虑运输规模经济。

假设由100个伐区向造纸厂供应2种不同的木材，造纸厂对两种木材的需求都为5 500 m3，备选集材区数量为10个。木材从伐区运往集材区、从伐区直接运往造纸厂、从集材区运往造纸厂的单位物流成本Cijk,Dik,Hjk为每立方米0.02元/km、0.025元/km和0.03元/km。设A1=0.1、A2=0.15、B1=1.1、B2=1.15。实验参数设置如表1所示，其中U(a,b)表示服从参数a和b的均匀分布。

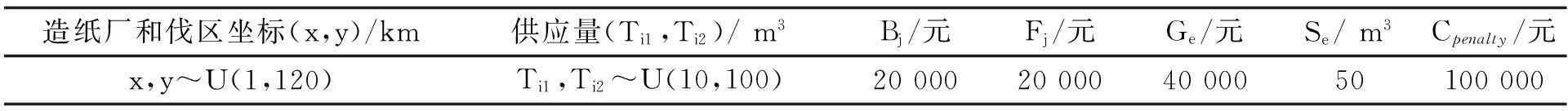
表1　参数设置

将上述数据作为模型输入，使用Gurobi工具进行求解，得到木材物流网络的总成本f=164 368元，联合机配置数量e=4，集材区木材加工生产线的数量wj=0，即不设置集材区节点。为了分析模型中参数改变对木材物流网络优化结果的影响，基于原模型输入数据，调整模型中有关参数，设计4个实验，实验结果分析如下。

①对模型的目标函数中参数进行敏感性分析

模型的目标函数f中有3组参数，即单位物流成本Cijk,Dik,Hjk、集材区配置成本(包括集材区固定成本Bj和生产线固定成本Fj)及联合机配置成本Ge。按照-75%，-50%，-25%，+25%，+50%，+75%调整三组参数大小，实验结果见表2。

表2　三组参数的敏感性分析

从表2中可以看出，单位物流成本Cijk,Dik,Hjk，对木材物流网络中物流成本(f1+f2+f3)影响显著，对木材物流网络总成本f影响不大。这是由于物流成本主要考虑运输成本，因此单位运输成本变化时，总物流成本将产生同比例的变化；而物流成本仅占木材物流网络总成本的比例不到3%，因此对木材物流网络的总成本影响极小。

当集材区的配置成本(Bj+Fj)按照+25%，+50%，+75%的比例变动时，木材物流网络中的物流成本(f1+f2+f3)和总成本f均不发生变化，这是因为当集材区的配置成本高于联合机配置成本时，为了使得总成本最小，木材物流网络将放弃集材区节点，即备选集材区均未被选中，造纸厂的所有木材需求由伐区直送满足。

联合机配置成本Ge对木材物流网络总成本影响显著，这是因为在伐区投入生产的联合机价格高，联合机成本的上升或下降对木材物流网络总成本影响极大。

②集材区配置成本与联合机配置成本变动对木材物流网络结构的影响

集材区配置成本(Bj+Fj)与联合机配置成本Ge的比较关系，是备选集材区节点是否被选中的关键因素，进而影响木材物流网络的结构，实验结果如表3所示。

表3　集材区配置成本与联合机配置成本对木材物流网络结构的影响

本实验中，当集材区配置成本(Bj+Fj)大于联合机配置成本Ge时，木材物流网络结构如图2所示，木材物流网络由伐区节点、造纸厂节点及伐区运往造纸厂的线路构成二级网络。从图2中可以看出，位于坐标(x,y)=(13,13)km处的造纸厂的木材需求由100个伐区满足。在二级网络结构中，采用一贯式木材运输模式，有利于提高运材效率，木材物流作业环节少，对减少污染、保护森林环境有积极意义。

当集材区配置成本(Bj+Fj)小于联合机配置成本Ge时，木材物流网络结构如图3所示，木材物流网络由伐区节点、集材区节点和造纸厂节点，以及木材从伐区运往造纸厂、从伐区运往集材区和从集材区运往造纸厂的线路构成了三级网络。从图3中可以看出，一个位于坐标(x,y)=(15,23)km处的备选集材区被选中，即部分木材在伐区砍伐后运至该集材区暂存，在造纸厂需要时将木材加工成木屑再运往造纸厂。节点之间的连线表示伐区对集材区、集材区对造纸厂和伐区对造纸厂的分配关系。三级网络结构中，集材区节点保有一定数量的木材库存，木材从供给点到需求点的运距大大缩短，降低了造纸厂原材料库存短缺的风险。

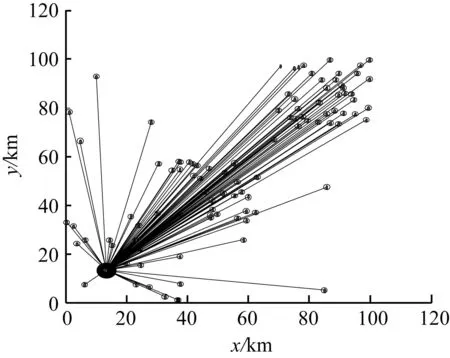
图2二级木材物流网络

Fig.2Two echelon timber logistic network

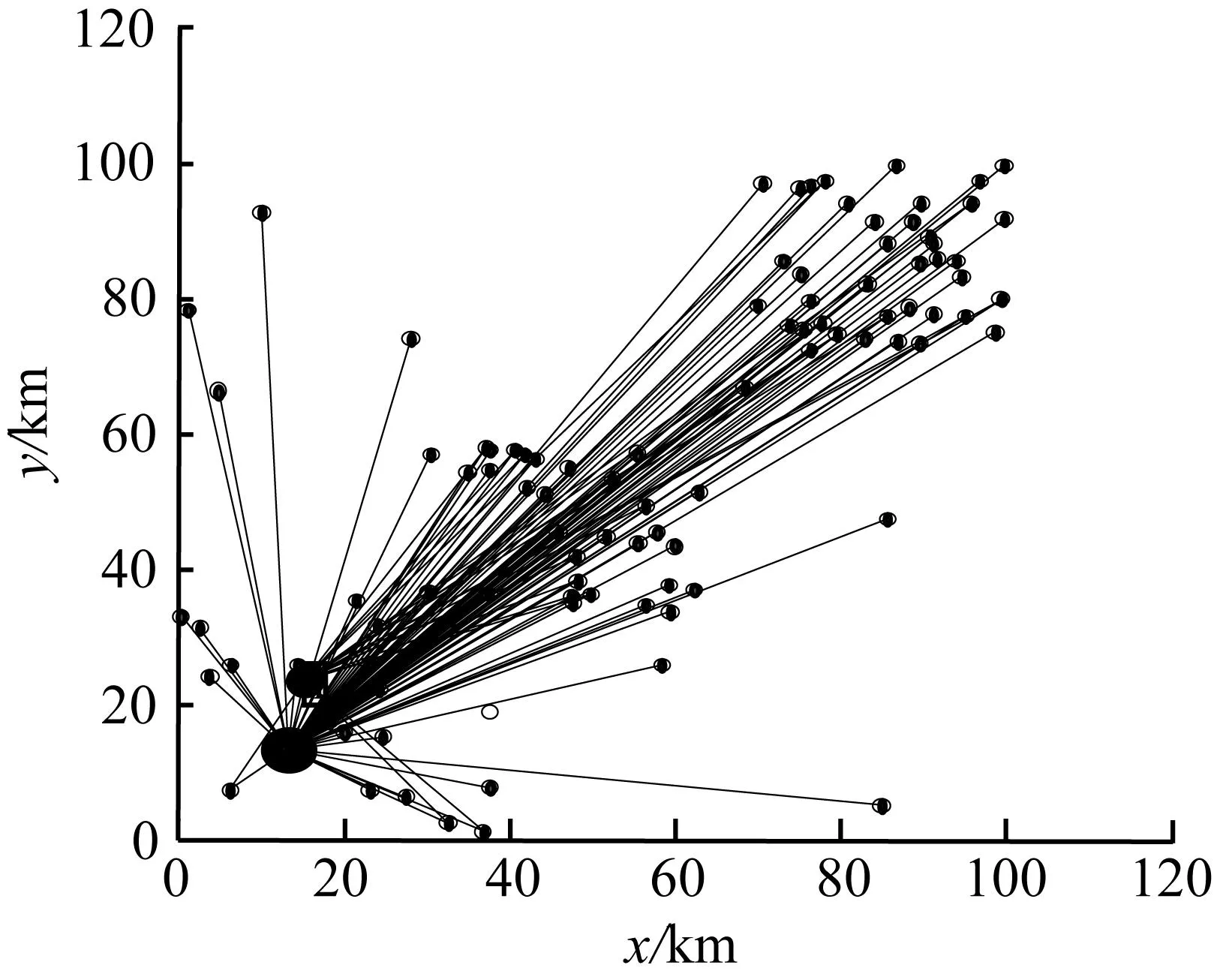
图3三级木材物流网络

Fig.3Three echelon timber logistic network

③联合机作业能力的影响分析

联合机作业能力对木材物流网络成本的影响如图4所示。当联合机作业能力Se按照-75%、-50%、-25%、+25%、+50%、+75%变动时，木材物流网络所需投入的联合机数量分别为9台、5台、4台、3台、3台、2台。相应的，木材物流网络中物流成本发生了15.04%、10.83%、15.04%、0.00%、0.00%、0.00%的变动，木材物流网络的总成本发生了146.41%、48.96%、0.40%、-24.34%、-24.34%、-48.67%的变动，可见，联合机作业能力显著影响木材物流网络的总成本。此外，当联合机作业能力较弱时，木材网络需设置集材区以满足造纸厂的需求；当联合机作业能力增强时，木材物流网络无需设置集材区，伐区的木材直接送往造纸厂，物流成本不再发生改变。

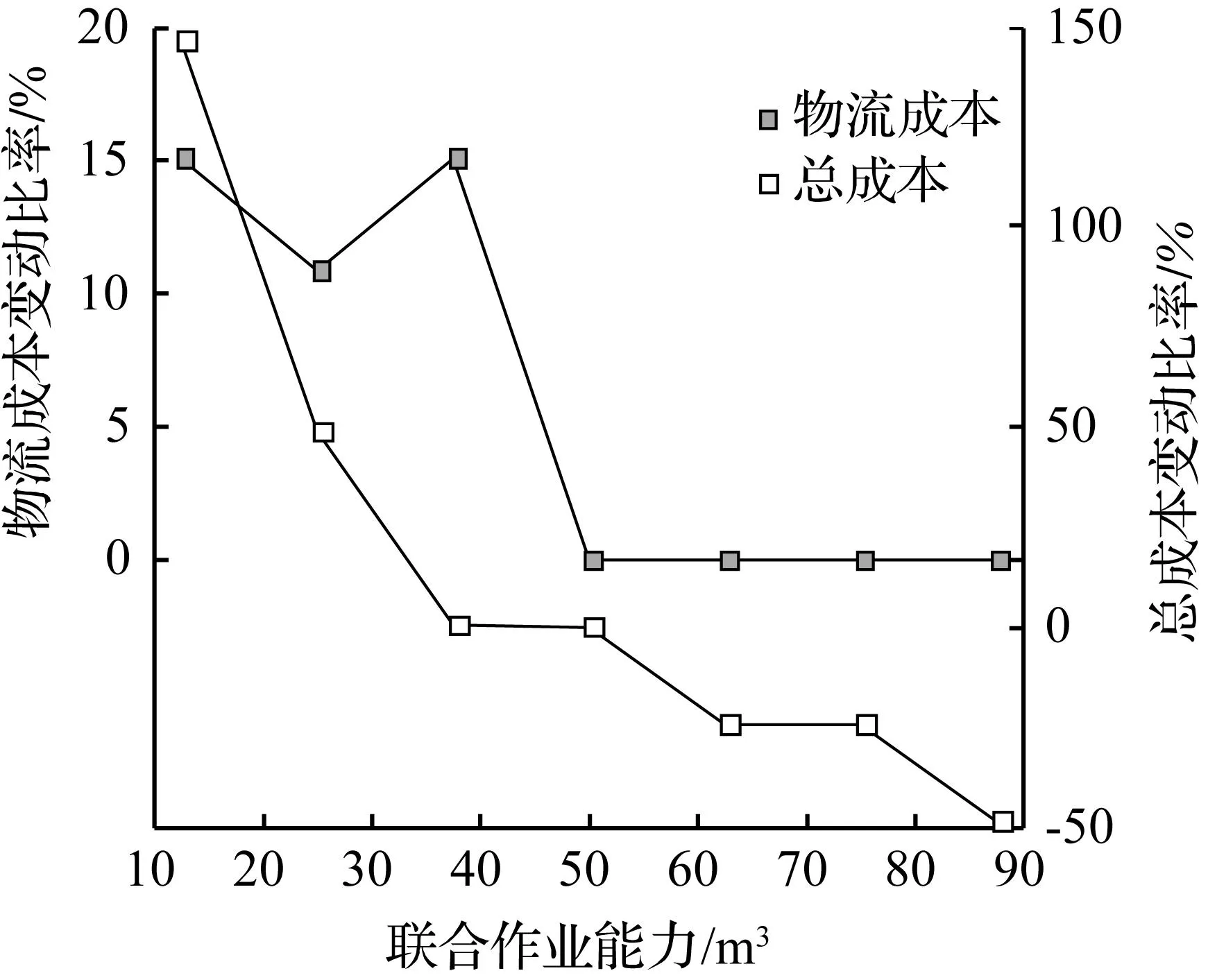
图4　联合机作业能力的影响Fig.4　Effect of the capacity of delimbing-debarking-chipping machine

④木材供需平衡分析

实验假定木材需求Nk为一个常数，对Nk按照-75%、-50%、-25%、+25%、+50%、+75%调整大小，实验结果如表4所示。

表4　木材需求变动对木材物流网络成本的影响

从表4中可以观察到，当木材需求减少25%、50%、75%时，木材供大于求，木材物流网络总成本f减少至64 772、43 182、41 092元。而当木材需求增加25%、50%、75%时，木材供不应求，相应的惩罚成本f7分别为21 600、49 100、76 600万元，木材物流网络总成本f急剧增加。这意味着，造纸厂可能因为缺乏原材料而停产造成巨额损失，或为了连续生产不得不以较高的价格从木材现货市场上购买原材料。

4结语

本文研究木材物流网络优化问题，以最小化木材物流网络总成本为目标，建立了一个混合整数规划模型，通过求解模型得到集材区的位置，集材区生产能力以及伐区联合机能力配置。考虑调整模型参数，设计了4组实验，通过算例分析得到结论：联合机配置成本及作业能力对木材物流网络的总成本影响显著；集材区配置成本与联合机配置成本的比较关系，决定木材物流网络的结构，是优化木材物流网络的关键；木材原材料供不应求时，造纸厂将付出巨大经济代价，因此，研究集材区选址及能力配置问题具有很强的现实应用意义。本文研究特定条件下的网络优化，在生产实践中需要进一步考虑其他约束，如本文仅考虑三级网络结构的优化，对于更加复杂的网络结构未予以分析，这将是未来工作的重点。

参考文献:

[1]陈诚,邱荣祖.多周期木材物流网络优化研究[J]. 福建林学院学报, 2014, 34(3): 274-278.

[2]MELO M T, NICKEL S, SALDANHA-DA-GAMA F, Facility location and supply chain management-a review[J]. European Journal of Operational Research, 2009, 196(1): 401-412.

[3]周静娴,肖玲,胡志华.基于双层随机规划的多时段募集点选址问题[J]. 广西大学学报:自然科学版, 2014,39(2): 365-371.

[4]王永富.基于供应链的广西木材物流系统建设研究[J]. 物流技术, 2012, 31(5): 182-185.

[5]CHAUHAN S S, FRAYRET J M, LEBEL L, Supply network planning in the forest supply chain with bucking decisions anticipation[J]. Annals Operation Research, 2011, 190(1): 93-115.

[6]FRISK M, COTHE-LUNDGREN M, JORNSTEN K,et al.Cost allocation in collaborative forest transportation[J]. European Journal of Operational Research, 2010, 205(1): 448-458.

[7]CARLSSON D, D’AMOURS S, MARTEL A, et al.Supply chain plannning models in the pulp and paper industry[J]. INFOR, 2009, 47(3): 167-183.

[8]陈诚,邱荣祖.基于混合整数规划模型的木材物流网络优化[J]. 中南林业科技大学学报, 2013, 33(1): 94-98.

[9]邱荣祖,林雅惠,钟聪儿.基于ArcGIS的木材物流中心选址[J]. 林业科学, 2010, 46(6): 113-117.

[10]张淑芬,邢艳秋,吴红波,等.基于GIS和RS技术的木材运输线路优化研究——以吉林省汪清林区为例[J]. 森林工程, 2011, 27(2): 48-60.

[11]刘俊.林纸供应链原料供应优化与仿真研究[D]. 南京：南京林业大学经济管理学院，2013.

[12]胡婷婷.基于林业绿色供应链的木材物流运作模式研究[D]. 内蒙古农业大学经济管理学院,2012.

[13]CHAN T, CORDEAU J F, LAPORTE G. Locating satellite yards in forestry operations[J]. INFOR, 2009, 47(3):223-234.

[14]孙长海,张冬冬.关于林业采运机械类型与应用的探讨[J]. 黑龙江科技信息, 2013(7): 215.

(责任编辑梁碧芬)

On integrated optimization of locating satellite yards and capacity assignments

PAN Jing-jing1, HU Zhi-hua2

(1.College of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou

350002, China；2.Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China)

Abstract:Since there existsthecontradictionbetween concentrated and seasonal supply of timber and the scattered and continuous demand of timber, the location of satellite yard and capacity assignments are studied, in order to minimize the total cost of timber logistics network.The problem is formulated as a mixed-integer linear program, and it issolved by Gurobi tool.Additionally, four experiments are designed and conducted by using different model parameters. A numerical example is given to verify the feasibility and effectiveness of the model. Based on the experimental results, the effectof changing model parameters on the optimization of timber logistics network is analyzed.

Key words:logistics management; timber logistics; location; mixed-integer program; logistics network

中图分类号：TP399; F253.4

文献标识码：A

文章编号：1001-7445(2015)06-1533-07

doi:10.13624/j.cnki.issn.1001-7445.2015.1533

通讯作者：胡志华(1977—)，男，湖南长沙人，上海海事大学教授; E-mail:zhhu@shmtu.edu.com。

基金项目：国家自然科学基金面上项目(71471109)；交通运输部科技计划应用基础研究项目(2015329810260)；上海市教委科研创新项目(14YZ100)；福建农林大学青年教师科研基金项目(2012xjj26)

收稿日期：2015-08-21；

修订日期：2015-10-01