输入电压纹波对并联buck变换器分岔和混沌的影响

谢玲玲，高善明，龚仁喜，黄　阳

(广西大学电气工程学院， 广西南宁530004)



输入电压纹波对并联buck变换器分岔和混沌的影响

谢玲玲，高善明，龚仁喜，黄阳

(广西大学电气工程学院， 广西南宁530004)

摘要：文中从纹波峰值、纹波的谐波阶数及初始相位角三方面深入研究了输入电压纹波对均流控制的并联buck变换器分岔和混沌行为的影响，并与输入电压不含纹波时的情况进行比较分析。结果表明，输入电压含纹波时的系统分岔图呈现扩展的带状结构，相应的庞加莱映射为环状结构，状态变量的时域波形在较长时间内表现为周期性谐波和次谐波振荡。可见输入电压纹波对系统的稳定性有较大的影响。实验也验证了理论分析和仿真结果的正确性。

关键词：并联buck变换器；分岔；混沌；纹波

DC/DC变换器是一类典型的非线性时变系统，存在着丰富的非线性动力学行为，如各种类型的分岔[1-3]、次谐波振荡[4-5]、混沌[6-8]等。对这些非线性现象的研究，有助于更好地理解其动力学规律，有利于开发设计更稳定可靠的变换器，从而提高产品的性能和质量。

单个变换器存在电流应力大、价格高等缺点，而并联变换器系统具有大容量、高效率、高可靠性、模块化以及低成本等优点[9-10]。因此，随着大功率输出需求的不断增长及分布式电源的迅速发展，多个变换器并联技术得到了广泛地应用。近年来，对DC/DC变换器的分岔和混沌研究也进一步拓展到并联变换器中[11-14]。然而，迄今为止，在对并联变换器分岔和混沌的研究报道中，通常将其输入电压假定为理想直流稳压电源，没有考虑输入电压含有纹波的情况。在实际应用中，变换器的输入电压大多是经过整流、滤波后得到的直流电源，都含有一定的纹波，而纹波对变换器系统的各种性能如稳定性、可靠性等有着较大的影响。在这种情况下，以传统理想直流电源为输入电压的变换器模型将与实际模型不一致，由此获得的结果也将与实际结果有所偏差。为此，本文以均流控制并联buck变换器为研究对象，考虑其输入电压含纹波时的情况，将输入电压表示为直流分量和纹波分量之和，建立相应的离散迭代映射，从数值仿真、理论分析等方面研究系统的非线性行为，并与输入电压为理想直流电源时的情况进行对比。从纹波峰值、谐波阶数、初始相位角三方面详细分析了输入电压纹波对系统非线性特性的影响。最后通过实验对文中的理论分析、仿真结果进行验证。

1均流控制并联buck变换器

1.1　工作原理

均流控制并联DC/DC变换器系统框图如图1所示[12]。变换器1、2的开关管S1、S2的驱动信号均由PWM脉冲信号驱动。PWM脉冲信号由控制信号Ucon与锯齿波信号Uramp比较产生，当Ucon>Uramp时，输出高电平，开关管导通；反之，输出低电平，开关管关断。

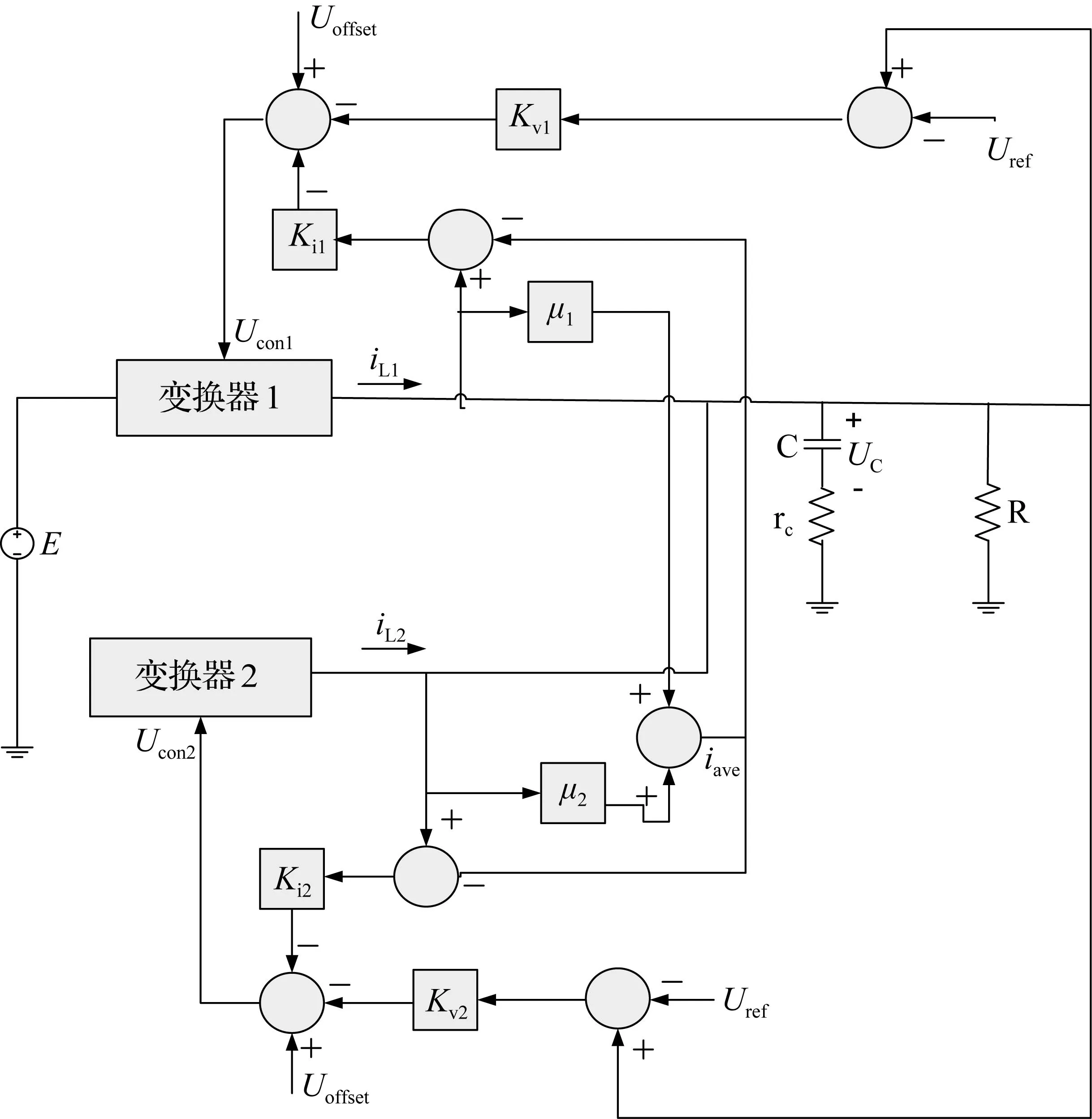
图1　均流控制并联DC/DC变换器系统框图

(1)

其中，UL和UU分别表示锯齿波信号的下限和上限，T表示锯齿波信号的周期。

由图1可得变换器1、2的控制信号表达式如式(2)、式(3)所示,即

Ucom1=Uoffset-Kv1(uC-Uref)-Ki1(iL1-iave)，

(2)

Ucom2=Uoffset-Kv2(uC-Uref)-Ki2(iL2-iave)，

(3)

式中，Uoffset表示稳态占空比的直流偏置电压；Uref表示参考电压；uC表示电容电压；iL1和iL2分别表示流过变换器1和变换器2的电感电流；Kv1、Kv2分别为变换器1、变换器2的电压反馈系数；Ki1、Ki2分别为变换器1、变换器2的电流反馈系数。iave表示平均电流，定义为：

iave=μ1iL1+μ2iL2，

(4)

式(4)中，μ1=μ2=1/2, 为常数。

1.2　离散迭代映射

并联buck变换器电路如图2所示。S1、VD1、L1组成图1中的变换器1，S2、VD2、L2组成变换器2，其中，rL1、rL2、rC分别为电感L1、L2、电容C的等效串联电阻。当电路工作在连续导电模式时，二极管Di与开关管Si状态互补(i=1,2)，即当Si导通，Di关断；反之亦然[21-22]。因此，在一个开关周期T内，电路有4种可能开关状态，即S1、S2都导通(模态a)； S1导通, S2关断(模态b)； S1关断(模态c), S2导通； S1、S2都关断(模态d)。

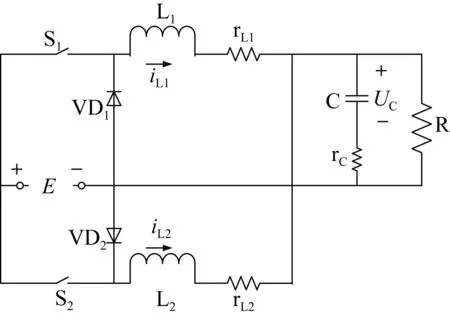
图2　并联buck变换器Fig.2　Schematic of parallel-connected buck converter

模态a、b、c、d相应的状态方程如下所示：

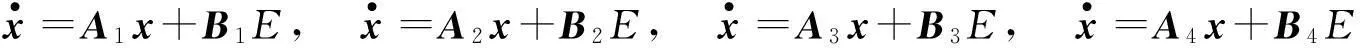
(5)

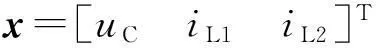
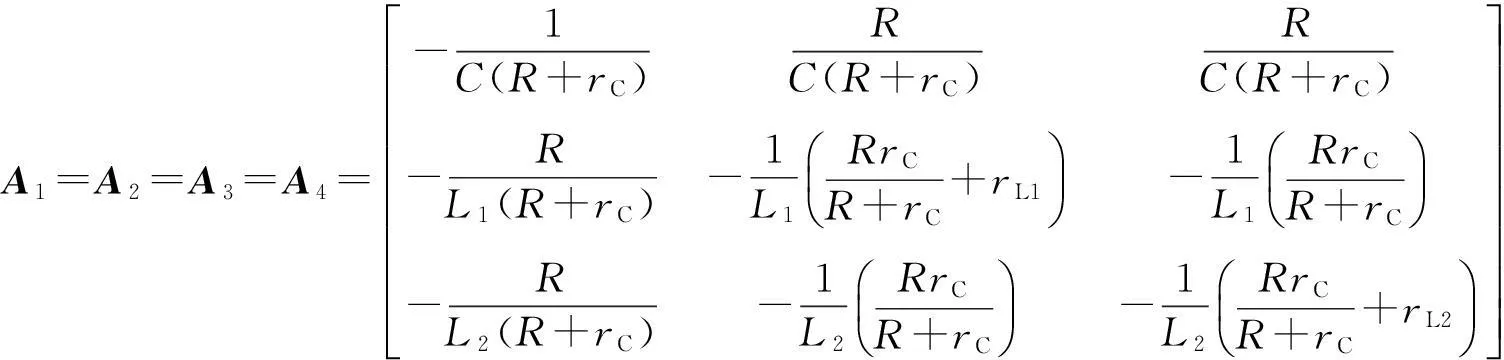
(6)

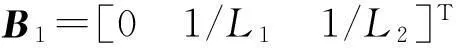
(7)

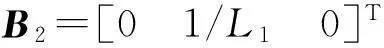
(8)

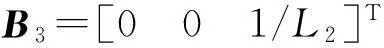
(9)

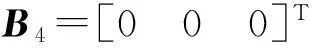
(10)

当输入电压含有纹波时，可将其表示为直流分量和纹波分量之和，即

E=Udc+Uripple，

(11)

式(11)中，Udc为输入电压的直流分量，Uripple表示纹波电压，其表达式为：

Uripple=Umsin(nωt+θ)，

(12)

其中，Um为纹波电压的峰值；n为纹波电压的谐波阶数；θ为初始相位角。

一般来说，假定并联buck开关变换器在1个周期内的开关顺序按式(5)进行，即从模态a开始，以模态d结束。但实际上，模态b和模态c取决于S1、 S2的导通时间，这两个模态在1个周期内不会同时出现。如果S1的导通时间大于S2，则可以忽略式(5)中的第3个式子；反之，则可以忽略式(5)中的第2个式子[12-13]。

2分岔行为及其分析

一般来说，在没有使用大的滤波电容情况下，经由一个标准的三相整流器整流后得到的直流电所含的纹波分量约为4%，而经由一个单相的整流器整流后要大于4%。因此，在没有使用大的滤波电容器的情况下，经单相整流器整流后得到的直流电压含10%的纹波分量是完全可能的。

仿真电路参数[13]：T=400 μs,Udc=48 V, 输出电压Uo=24 V，L1=0.02 H，L2=0.04 H，rL1=0.05 Ω，rL2=0.2 Ω，C=47 μF，rC=0.01 Ω，R=10 Ω，Kv2=3.5，Ki1=1，Ki2=1。假设变换器的输入电压是经过一个单相二极管整流后得到的，它含有频率为100 Hz的10%的纹波分量，则在式(12)中，Um=0.1Udc,n=2,ω=314,θ=0。在实际电路中，输入纹波电压的过零点与时钟脉冲可能有轻微的不同步，θ最大可达到为1.2°，但这对结果的影响可以忽略不计。

2.1　纹波对分岔的影响

图3(a)、图3(b)分别是输入电压为理想直流电源和直流电源含10%纹波分量的以Kv1为分岔参数的分岔图。从图3(a)可以清楚地观察到系统从稳态周期1到周期2、周期4的倍周期分岔现象；但图3(b)中，周期1到周期2的分岔转变并不明显可见。当2≤Kv1≤2.96时，由图3(a)可以看出系统处于稳定周期1状态，此时Kv1与输出电压是一对一的关系，在图中表现为单个点形式；而在图3(b)中，Kv1与输出电压是一对多的关系，在图中表现为扩展带状结构。在Kv1=3~5时，图3(b)中呈现上下两个扩展的带状结构。图3(b)中出现扩展带状结构的原因是输入电压纹波对系统存在一定的影响。

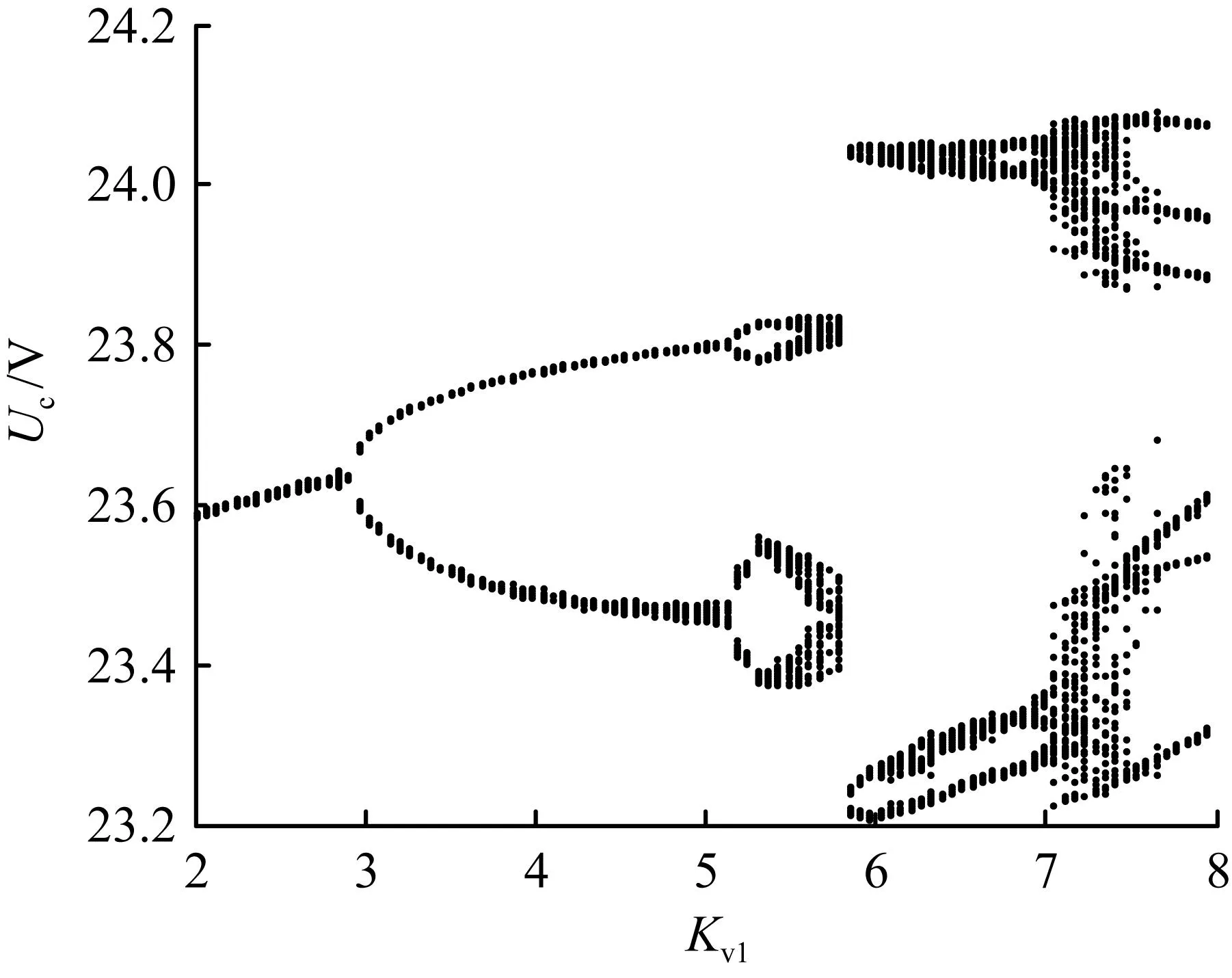
(a) 输入电压为理想直流电源

(b) 输入电压含10%纹波分量

图3以Kv1为变量的分岔图

Fig.3Bifurcation diagram withKv1as bifurcation parameter

2.2　纹波峰值对分岔的影响

图4示出了输入电压含5%纹波分量时，以Kv1为分岔参数的分岔图，此时，纹波的峰值为0.05Udc。由图4与图3(b)的对比分析可知，当增大(减小)纹波分量时，分岔的基本结构与纹波大小无关，但其相应的状态变量的值的变化范围增大(减小)。

2.3　纹波谐波阶数对分岔的影响

图5示出了纹波阶数n=3的分岔图(其余参数与图3(b)相同)。由图5和图3(b)的对比分析可知，二者的分岔基本结构相同，但当增大(减小)纹波谐波阶数n时，其相应的状态变量的值的变化范围增大(减小)。

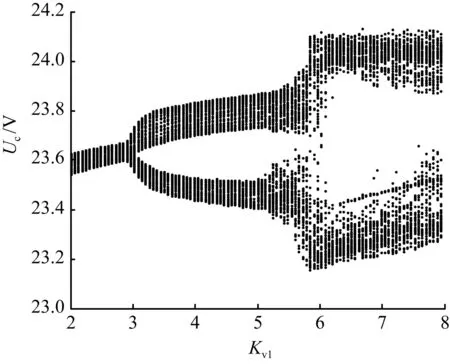
图4输入电压含5%纹波分量的分岔图

Fig.4Bifurcation diagram with 5%

ripple content in input voltage

图5n=3的分岔图

Fig.5Bifurcation diagram withn=3

3数值仿真及其分析

3.1　纹波对系统的影响

根据系统的离散迭代映射模型，采用龙格—库塔算法进行数值仿真，研究纹波对系统谐波、次谐波振荡以及混沌行为的影响。

当输入电压含10%纹波分量，Kv1=2时的系统仿真波形如图6所示。在很短的时间内，如几个周期内，所观察到的电感电流iL2波形没有明显地变化[参见图6(a)]，与输入电压为理想直流电源的稳态周期1波形一致；但在较长时间内观察到的电感电流iL2波形则呈现周期性振荡，振荡周期为0.01 s[参见图6(b)]。这是因为输入电压纹波对系统有一定的影响，仅在短时间内没有影响。从图3(a)可知，当Kv1=2且输入电压为理想直流电源时的并联buck变换器处于稳定周期1状态，此时，相应的庞加莱映射是一个点；而输入电压含10%纹波的变换器的庞加莱映射则为1个由25个点组成的单环[参见图6(c)]。其原因是输入电压带纹波的变换器除了自身的自然振荡频率以外，还存在2个由外力驱动产生的频率，一个是开关频率fs=2 500 Hz，另一个为纹波的频率f=100 Hz，这两个频率的比为1/25。因此，其庞加莱映射为1个由25个点形成的环。相应的相图如图6(d)所示。

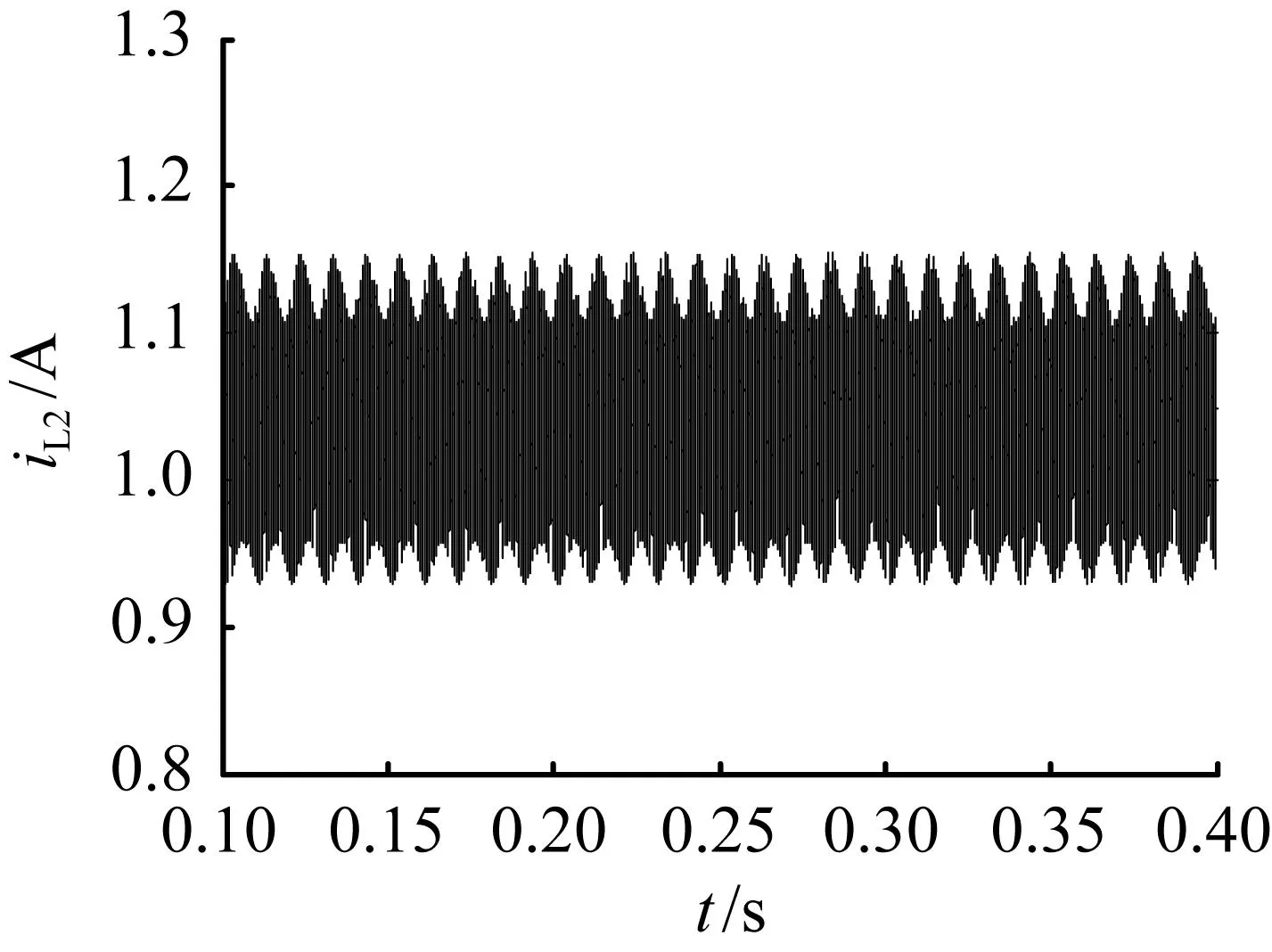
图7 为输入含10%纹波Kv1=5时的系统仿真波形。如图7(a)~(b)所示，电感电流iL2波形在几个周期时间内表现为次谐波振荡，没有明显变化；但在长时间内其波形表现为具有周期性的次谐波振荡，振荡周期为0.01 s。从图3(a)可知，当Kv1=5时，输入电压为理想电压的变换器发生倍周期分岔后进入周期2状态，此时，其相应的庞加莱映射应为两个点；而输入电压含10%纹波分量的变换器发生分岔后进入周期性次谐波振荡，系统相应的庞加莱映射为两个环[参见图7(c)]，这两个环分别对应于图3(b)中的上下两个扩展的带状结构。

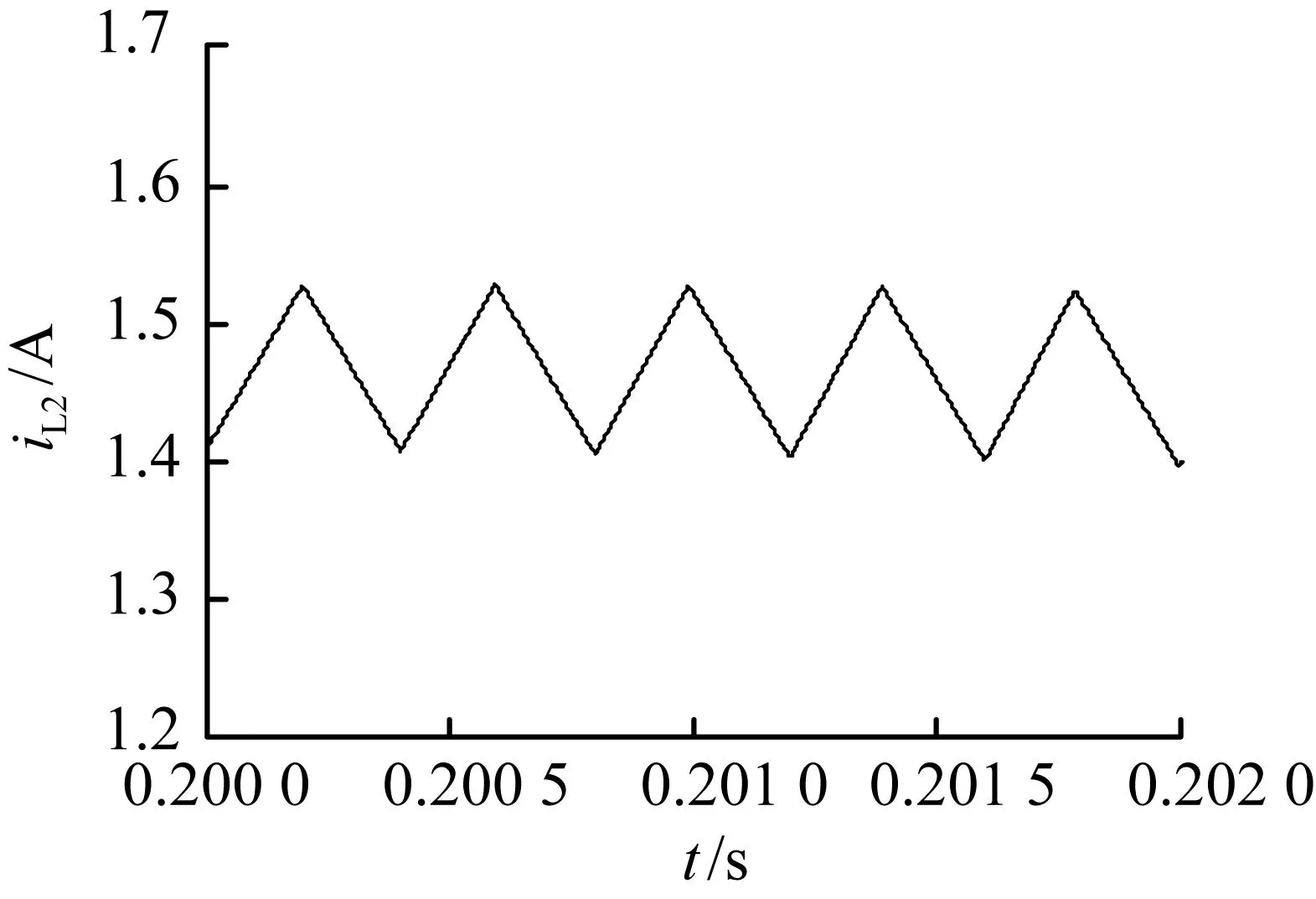
(a) 电感电流iL2时域图(局部放大)

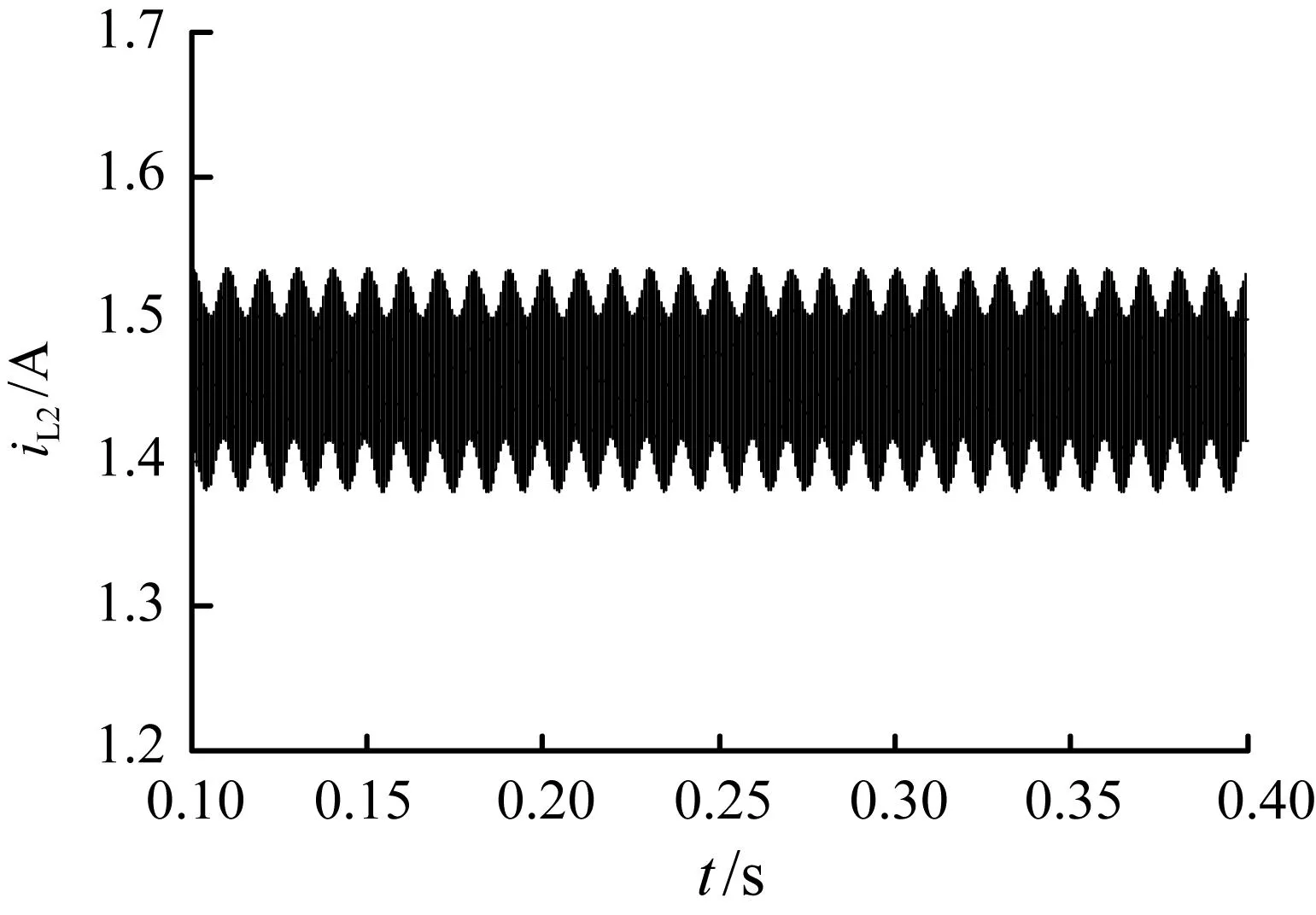
(b) 电感电流iL2时域图

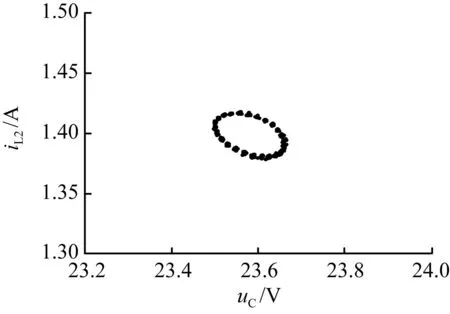
(c) 电容电压uC与电感电流iL2的庞加莱映射

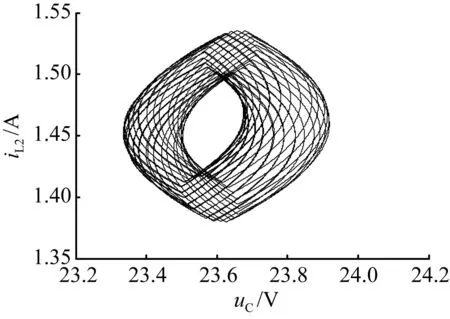
(d) 电容电压uC与电感电流iL2相图

图6输入电压含10%纹波分量Kv1=2时仿真波形

Fig.6Simulation waveforms forKv1=2 with 10% ripple content in input voltage

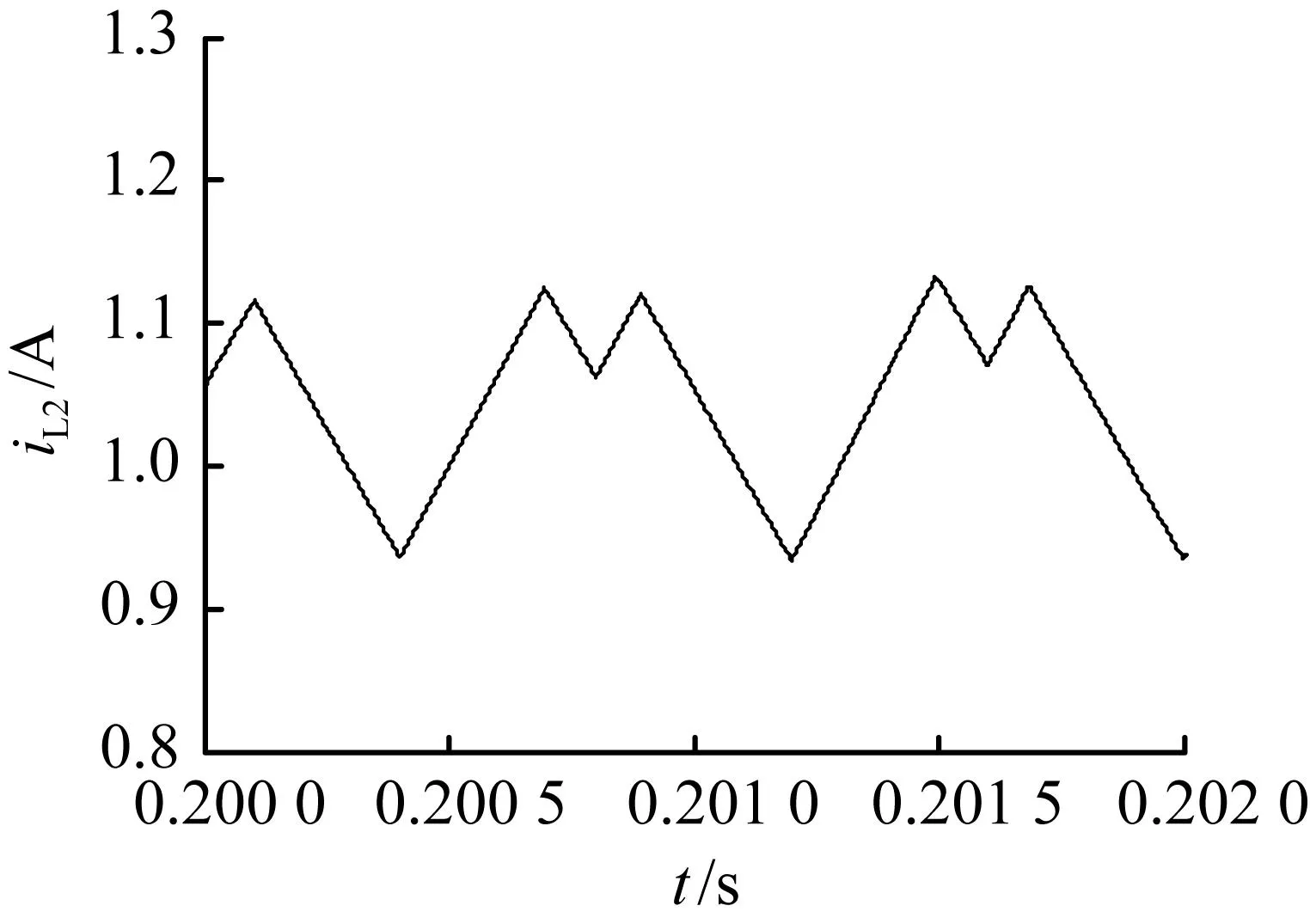
(a) 电感电流iL2时域图(局部放大)

(b) 电感电流iL2时域图

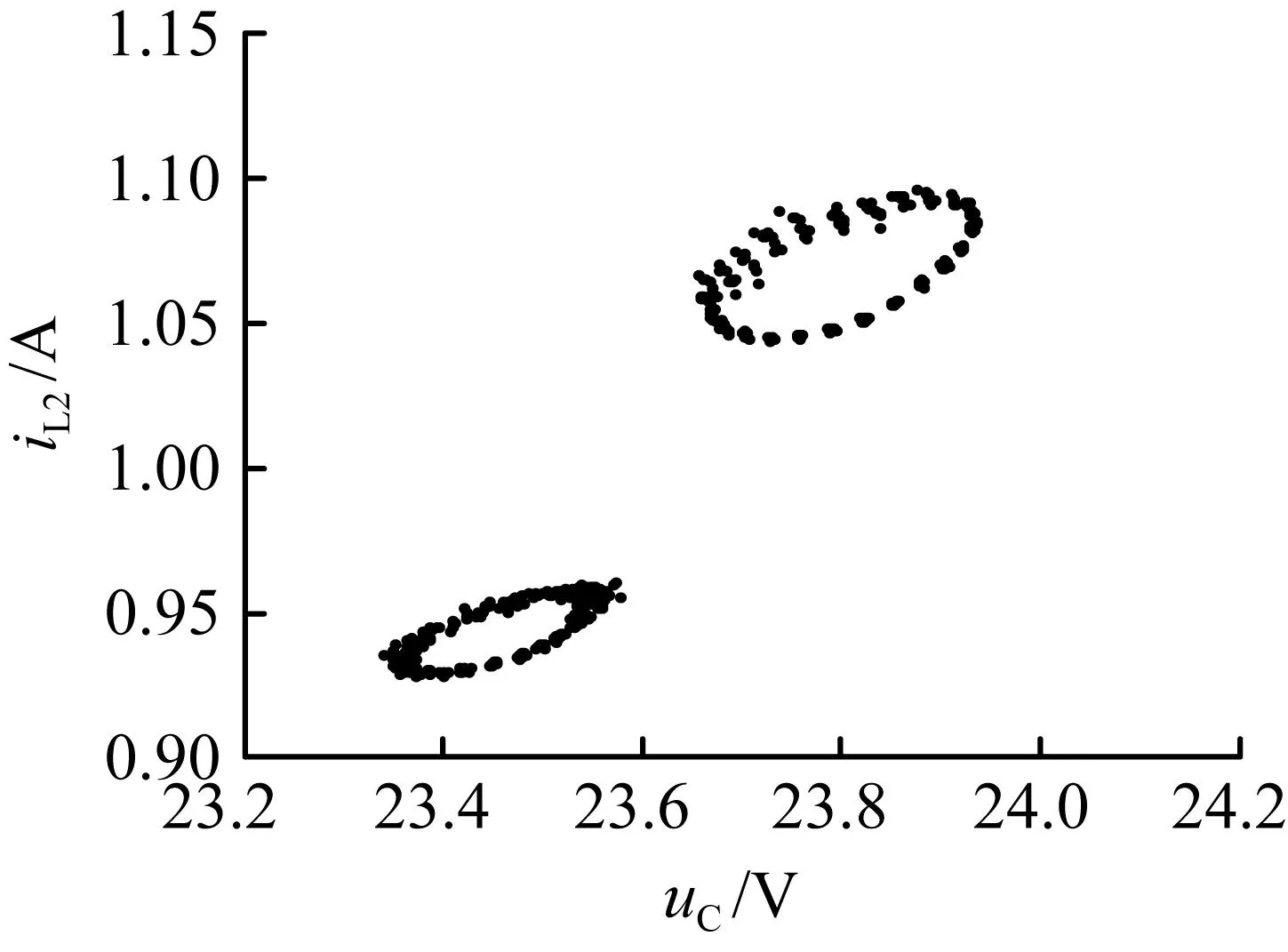
(c) 电容电压uC与电感电流iL2的庞加莱映射

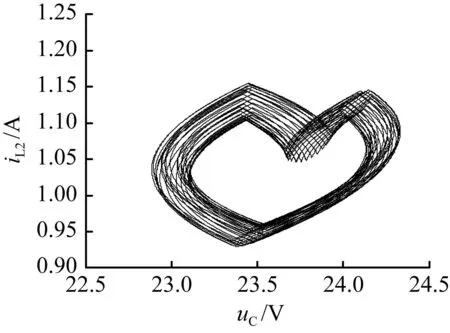
(d) 电容电压uC与电感电流iL2相图

图7输入电压带10%纹波Kv1=5时仿真波形

Fig.7Simulation waveforms forKv1=5 with 10% ripple content in input voltage

3.2　纹波峰值对系统的影响

图8为输入电压纹波分量为5%庞加莱映射图(其余参数与图7相同)。由图8、图7(d)的对比分析可得，随着纹波分量增大(减小)，相应庞加莱映射的两个环的面积增大(减小)。

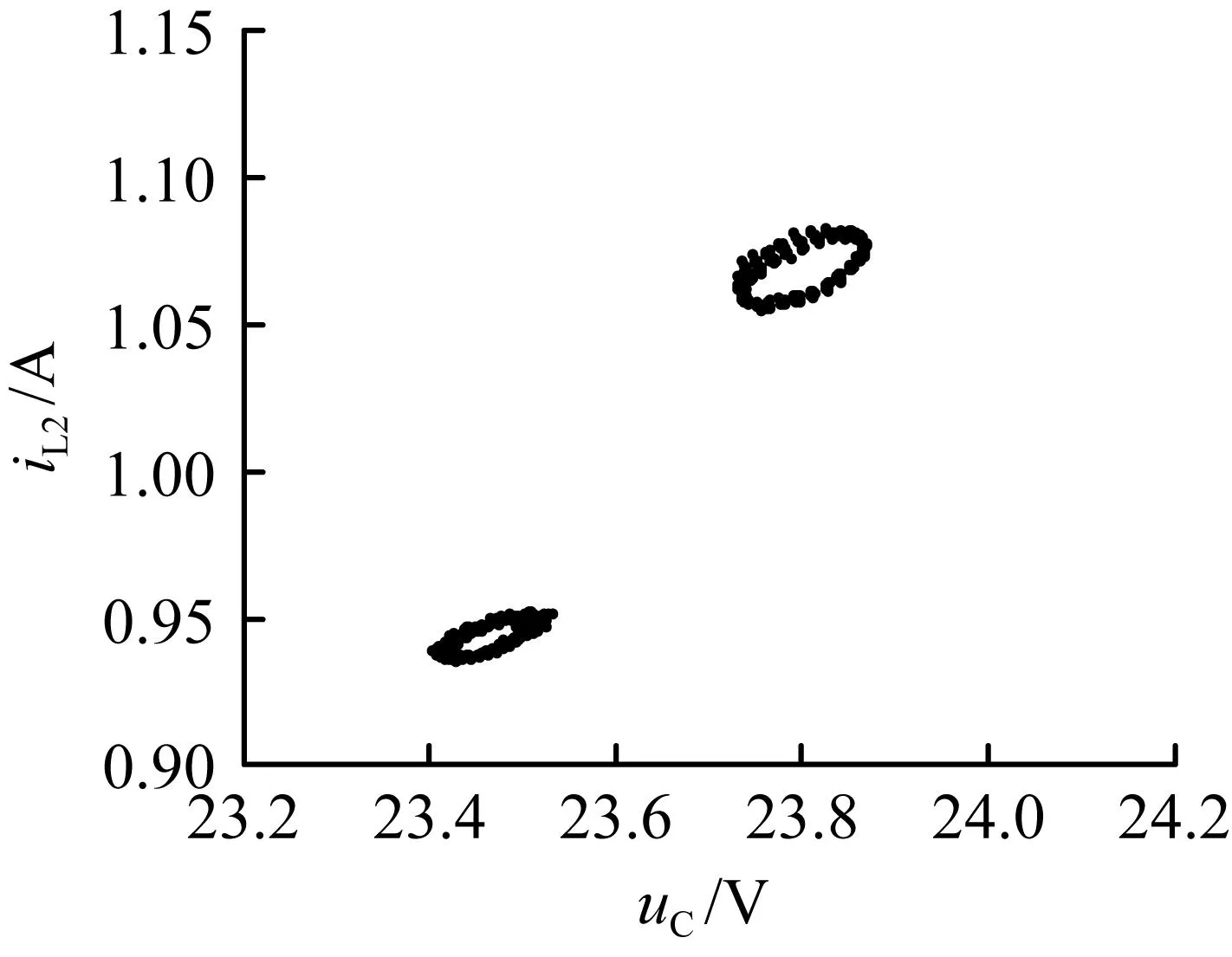
图8　输入电压含5%纹波分量的庞加莱映射图Fig.8　Poincaré mapping with 5% ripple content in input voltage

3.3　纹波谐波阶数对系统的影响

图9为n=3时的系统仿真波形(其余参数与图7相同)。由图9可知，电感电流的次谐波振荡周期约为6 700 μs，相应庞加莱映射为17个点组成的环。这是因为当n=3时，纹波频率f=150 Hz，此时它与变换器开关频率比约为1/17。与图7对比可知，当纹波阶数增大(减小)时，状态变量的次谐波振荡周期减小(增大)，与变换器开关频率的比率减小(增大)，庞加莱映射中组成环的个数减小(增大)。

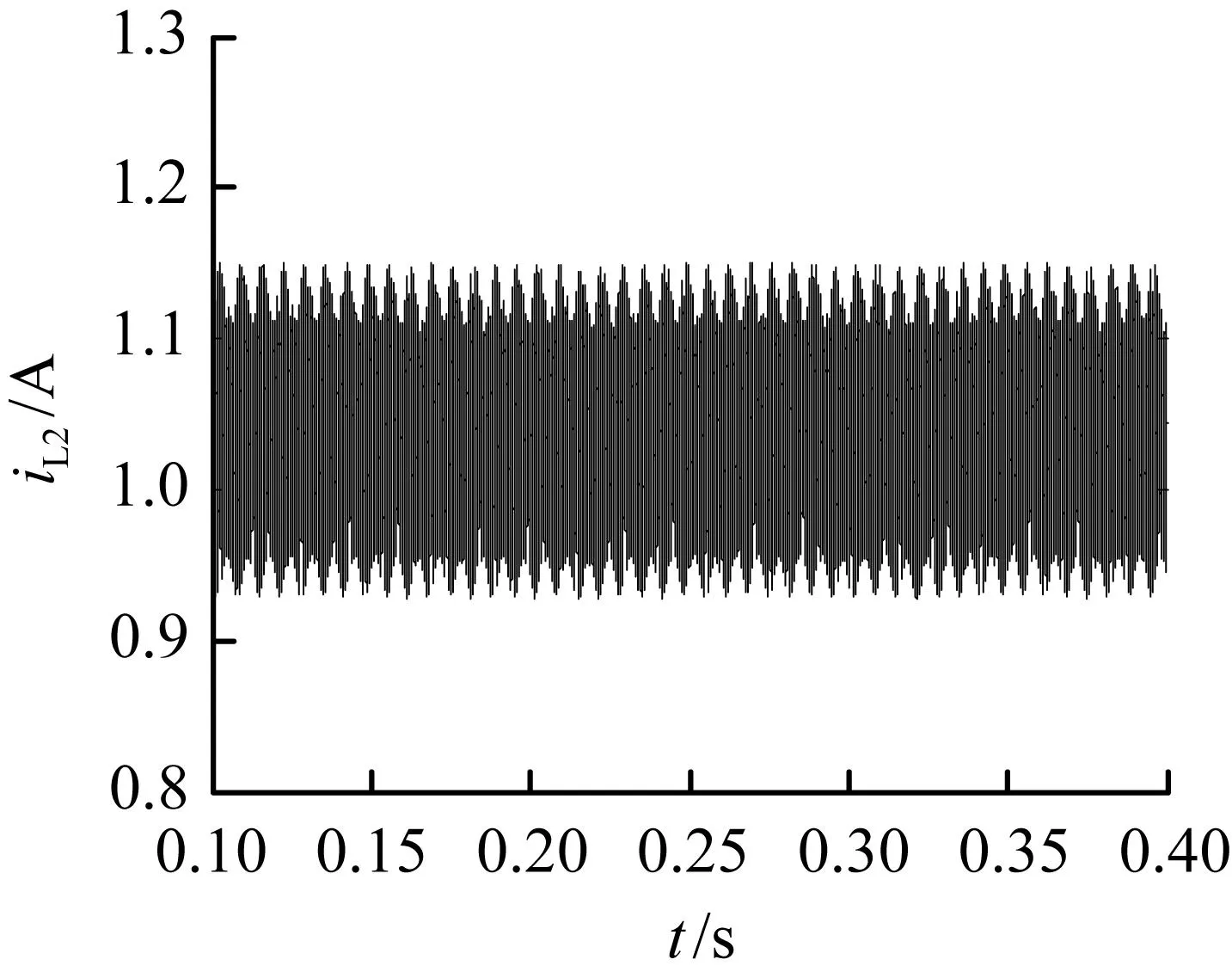
(a) 电感电流iL2时域图

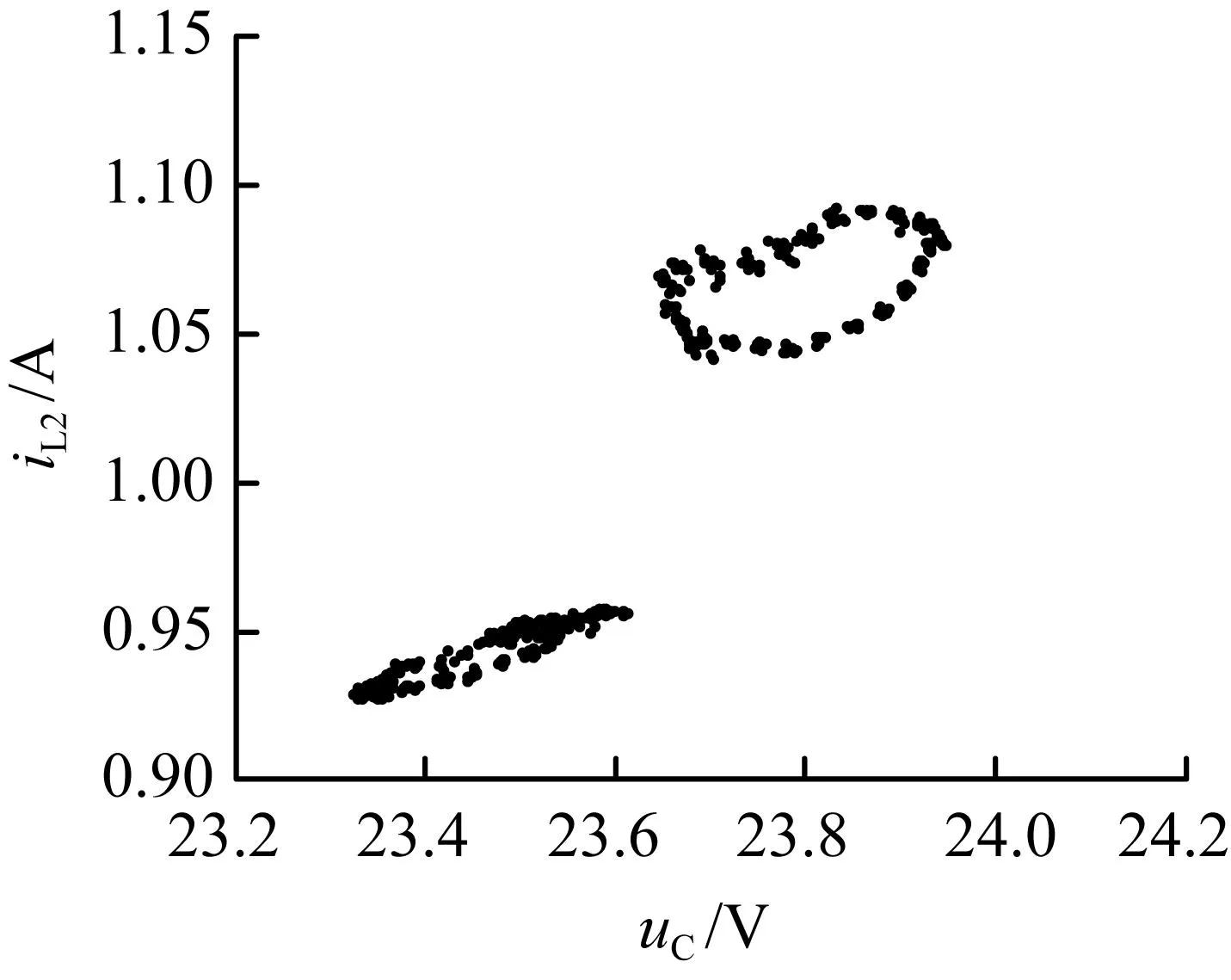
(b) 庞加莱映射

图9n=3时的仿真图

Fig.9Simulation waveforms forn=3

4 实验验证

为验证理论分析与仿真的正确性，进行相关的实验研究，实验中输入电压纹波的谐波次数为2次，其他参数与仿真参数一致。图10~图13分别给出了Kv1=2，Kv1=5时的时域波形及相图的实验波形。从图中可以看出，电感电流的波形呈现周期性谐波振荡。实验相图与仿真相图基本一致。与仿真相图相比，实验相图略有倾斜，这是因为实验电路存在寄生参数。

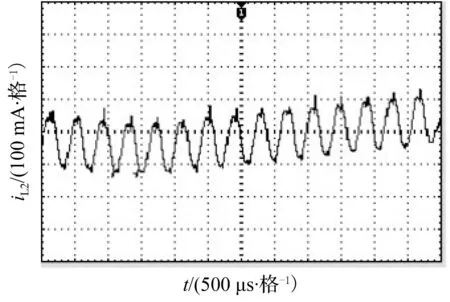
(a) 电感电流iL2波形(局部放大)

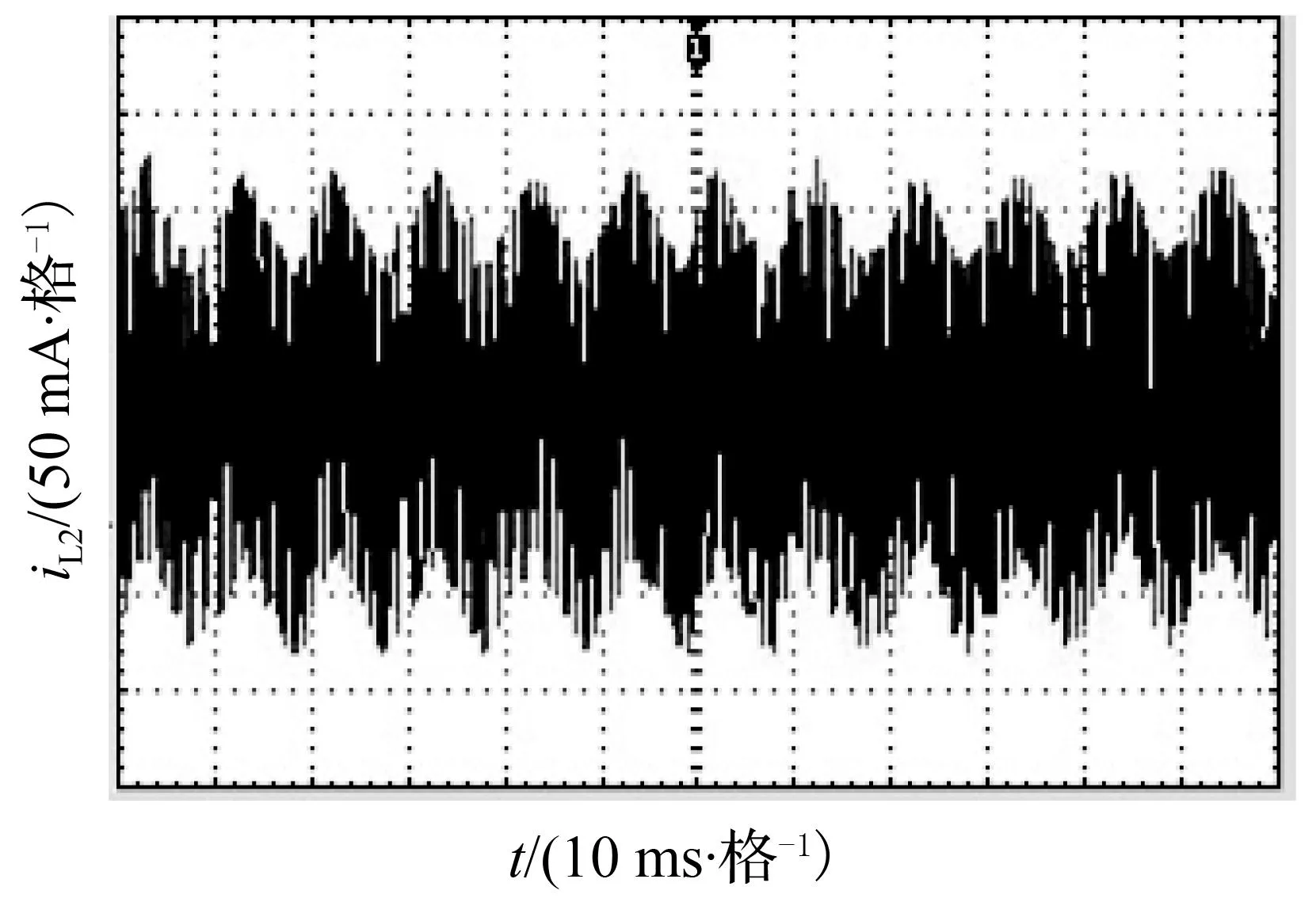
(b) 电感电流iL2波形

图10Kv1=2实验波形

Fig.10Experiment waveforms forKv1=2

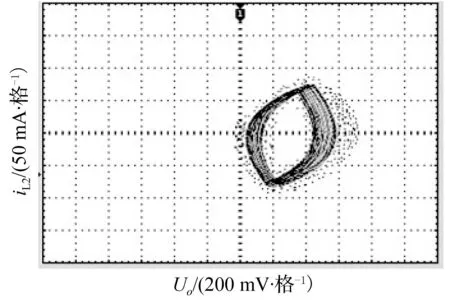
图11　Kv2=2时输出电压Uo与电感电流iL2相图

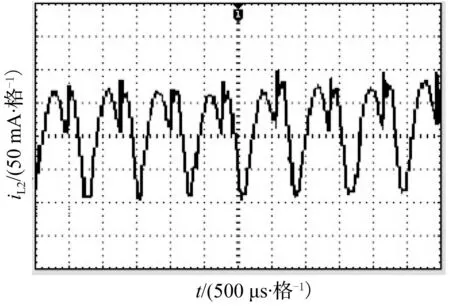
(a) 电感电流iL2波形1(局部放大)

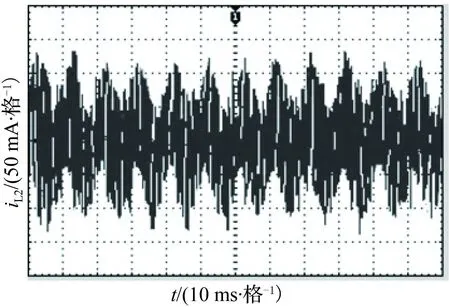
(b) 电感电流iL2波形2

图12Kv1=5实验波形

Fig.12Experimental waveforms forKv1=5

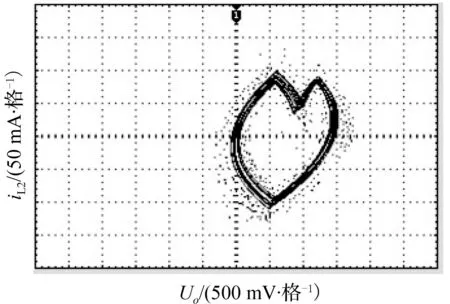
图13　Kv2=5时输出电压Uo与电感电流iL2相图

5结语

在实际应用中，DC/DC变换器的输入电压可能存在含纹波分量的情况，因此，本文详细分析了输入电压纹波对均流控制并联buck变换器分岔和混沌的影响。研究发现，并联buck变换器输入电压含纹波时的系统分岔图、次谐波振荡和混沌行为与输入电压为理想直流电源时的情况有很大的不同之处，表现在：①在分岔图中不能清晰地观察到系统从周期1到周期2的分岔转变，并且分岔图呈现扩展的带状结构。相应的庞加莱映射呈现为单环、双环形式。系统的周期决定环的个数，开关频率和纹波频率的比值决定组成环的点的数目。②状态变量的时域波形在较长时间内表现为周期性谐波和次谐波振荡，仅在几个周期时间内没有明显变化。

研究结果表明：当时间很短时，如几个周期时间，输入电压纹波对系统没有影响，但当时间稍长的时，它对系统的稳定性有着较大的影响。其影响具体表现为：①输入电压纹波的峰值和纹波的谐波阶数影响系统状态变量的值的变化范围，峰值越大，谐波阶数越大，值的变化范围就越大，相应庞加莱映射的环的面积就越大。②纹波的谐波阶数影响电感电流次谐波振荡周期和庞加莱映射中组成环的个数。随着谐波阶数的增大(减小)，状态变量的次谐波振荡周期减小(增大)，庞加莱映射中组成的环个数减小(增大)。③初始相位角对系统的影响可以忽略不计。

实验结果与理论分析、仿真结果一致，验证了理论的正确性。本研究进一步拓宽了开关变换器的非线性研究的拓展，有助于更深入地研究其动力学行为，对实际系统的稳定性和优化设计具有重要的指导意义。

参考文献：

[1]谢玲玲，龚仁喜，李畸勇.光伏发电最大功率点跟踪交错并联Boost变换器的动力学特性分析[J]. 中国电机工程学报，2013，33(6)：38-45.

[2]周宇飞，陈军宁.电流模式控制Boost 变换器中的切分叉及阵发混沌现象[J]. 中国电机工程学报，2005，25(1)：23-26.

[3]WU Xiao-qun, WONG Siu-Chung, CHI K T, et al.Bifurcation behavior of spice simulations of switching converters: a systematic analysis of erroneous results[J]. IEEE Trans On Power Electronics, 2007, 22(5): 1743-1752.

[4]谢帆，杨汝， 张波 .电流反馈型Buck 变换器二维分段光滑系统边界碰撞和分岔研究[J]. 物理学报，2010，59(12)：8393-8406.

[5]谢玲玲，龚仁喜，卓浩泽，等.电压模式控制不连续传导模式boost变换器切分岔研究[J]. 物理学报，2012, 61(5): 1-7.

[6]邹建龙，马西奎，杨宇.功率因数校正 Boost 变换器中慢时标分岔的影响因素分析与分岔控制[J]. 中国电机工程学报，2010，30(3): 1-7.

[7]XIE L L, GONG R X,ZHUO H Z, et al.Investigation of the mechanism of period-doubling bifurcation in voltage mode controlled buck-boost converter [J]. Journal of Electrical Engineering & Technology, 2011, 6(4): 519-526.

[8]谢玲玲，龚仁喜，王旷，等.电流模式控制Buck-Boost变换器非线性行为研究[J]. 电测与仪表，2010,47(540):4-7.

[9]GIAOURIS D,BANERJEE S, ZAHAWI B, et al.Stability analysis of te continuous-conduction-mode buck converter via filippov’s method[J]. IEEE Trans on Circuit and System-I, 2008, 55(4):1084-1096.

[10]周宇飞，姜丹丹，黄家成，等.DC-DC 变换器中负载阻抗特性及其对稳定性的影响[J]. 中国电机工程学报, 2010, 30(6):15-21.

[11]HUANG Yue-hui, CHI K T.Circuit theoretic classification of parallel connected DC-DC converters[J]. IEEE Trans on Circuit and System-I, 2007, 54(5):1099-1108.

[12]IU H H C, TSE C K.Bifurcation behavior in parallel-connected buck converters[J]. IEEE Trans on Circuit and System-I, 2001, 48(2):233-240.

[13]IU H H C, TSE C K.Bifurcation behavior in parallel-connected buck converters under a democratic current sharing scheme[C]//IEEE International Symposium on Industrial Electronics. Pusan, Korea: IEEE, 2001.

[14]谢玲玲，龚仁喜.交错并联boost变换器分岔和混沌行为研究[J]. 广西大学学报:自然科学版，2014,39(2)：393-399.

[15]吴俊娟，邬伟扬，孙孝峰.并联Buck 变换器中的混沌研究[J]. 中国电机工程学报，2005，25(11)：51-55.

(责任编辑裴润梅)

Effect of input voltage ripple on the bifurcation and chaos in parallel-connected buck converters

XIE Ling-ling, GAO Shan-ming ,GONG Ren-xi, HUANG Yang

(College of Electrical Engineering, Guangxi University, Nanning 530004, China)

Abstract:The effect of input voltage ripple on the bifurcation and chaos in a parallel-connected buck converter under current sharing control has been explored from the aspects of its peak value, the order of the harmonic and the initial phase angle. A comparison between the input voltage with and without ripple has been carried out. It is found that an expanding band-like structure can be observed in the bifurcation diagram, and a loop-type structure exists in the corresponding Poincaré mapping. The time-domain waveforms of the state variables display periodic harmonic and sub-harmonic oscillation in long span, which shows that the input voltage ripple has great effect on the stability of the system. The correctness of the theoretical analysis and simulation is verified by experiments.

Key words：parallel-connected buck converter; bifurcation; chaos; ripple

中图分类号：TM464

文献标识码：A

文章编号：1001-7445(2015)05-1438-09

doi:10.13624/j.cnki.issn.1001-7445.2015.1438

通讯作者：谢玲玲(1980—)，女，广西昭平人，广西大学副教授，博士；E-mail:xielingling1318@163.com。

基金项目：广西自然科学基金资助项目(2014GXNSFBA118277)；广西大学科研基金资助项目(XJZ130353) ；广西高校大学生创新创业计划项目(201410593080)

收稿日期：2015-04-28；

修订日期：2015-08-05