初中数学教学中数学模型思想的渗透研究

蔡宏

[摘 要] 数学模型，是指人们遇到一个数学问题以后，抽出数学问题的要点，发掘数学因素之间的内在联系，结合这套内在联系提出一个解决数学问题的规律，这一数学规律能够解决该类问题的公式. 本文提出了初中数学教学中数学模型思想渗透的意义，论述了初中数学教学中数学模型思想渗透的要点，结合教学实践指出了初中数学教学中数学模型思想渗透的方法.

[关键词] 初中；数学；数学模型；思想；渗透

为了提高初中数学教学的质量，提高学生解决数学问题的水平，教师要在数学教学中渗透数学模型思想.

初中数学教学中数学模型思想

渗透的意义

在初中数学教学中，数学教师常常会发现：部分学生不能灵活地应用学过的数学知识解决数学问题，他们遇到数学问题时，经常会去翻看课本中是否有类似的数学案例，如果发现有类似的案例，便用“依葫芦画瓢”的方法解决数学问题；如果没有类似的案例，便不去尝试思考解决数学问题的方法. 以上的数学教学现状说明很多学生欠缺解决数学问题的能力.

如果初中数学教师能够引导学生学会建立数学模型，学生就能在学习建立数学模型的过程中提高解决数学问题的能力.

初中数学教学中数学模型思想

渗透的要点

1. 结合学生的生活，引导学生理解数学建模的意义

数学建模的过程，是一个把具象数学问题变成一个抽象数学问题的过程.

对部分初中学生来说，研究抽象的数学知识过于枯燥、过于艰深，有时他们很难迅速地理解数学建模的要点. 如果学生不能在学习数学建模的过程中感受到学习数学知识的乐趣，他们就可能会放弃数学建模的学习. 数学教师只有在开展教学以前，结合学生的生活做好数学建模导入的设计，才能使学生感受到数学建模知识是来源于生活的需要，他们学习数学建模的知识是为了优化生活. 当学生理解到学习数学模型的意义以后，便会愿意自主地吸收相关的知识.

2. 结合学生的层次，引导学生分析数学建模的重点

初中生的层次具有差异性. 部分学生的数学基础好、领悟能力强，数学教师只要说明学习数学建模知识的要点，他们便能立刻用数学建模的方法解决数学问题. 然而这类学生所占比例不多，数学教师不能以此类学生吸收数学知识的速度为标准引导学生学习. 为了让学生学会分析数学建模的重点，教师要在教学中逐步分解数学问题，引导学生自主地发现数学建模问题的重点，从而掌握数学建模的原理.

3. 结合学生的思考，引导学生掌握数学建模的方法

当学生理解了数学建模的原理以后，教师要引导学生学会应用数学建模模型，能够在解决问题的过程中验证数学问题的模型. 数学教师只有引导学生灵活地应用数学建模模型知识，学生才能学会应用建模的思路解决各类数学问题，提高解决数学问题的能力.

初中数学教学中数学模型思想

渗透的方法

为了说明初中数学教学中教师渗透数学模型思想教学的方法，现用一则数学模型思想渗透的方法来说明.

1. 引导学生发现规律

部分初中生在解决数学问题的时候，存在以下几种意识：第一种为被动地等待数学问题出现的心理，由于受到旧教学体制的影响，部分数学教师在开展教学时直接提出数学问题，然后要求学生必须学习解决这些数学问题，因此，很多学生产生被动的学习思想，导致他们在面对数学问题的时候，不会主动地分析数学问题，只会待别人提出学习要求，告诉他们应该去解决哪些问题；第二种为盲目地对待数学问题，部分学生的思维层次较低，他们在没有遇到数学问题以前，没有意识到树立数学建模意识的重要性，等到遇到较为复杂的数学问题时，学生才发现找不到解决数学问题的方法，于是开始盲目地翻数学课本和教科书. 为了让学生树立数学建模的思想，了解数学建模的意义，数学教师要结合学生的生活主动地去发现数学问题，然后提出解决数学问题的目标.

以教师引导学生学习《概率帮你做估计》一课为例，有一名数学教师在开展教学的时候，结合一个数学游戏引导学生思考概率的问题：甲和乙打赌，在封闭的箱中有四个外观一样的小球，球上分别写1，2，3，4这四个数字，甲先抽一个球，球不放回；乙再抽一个球，若两个球相加的数字为奇数，则视为甲胜；反之若相加的数字为偶数，则视为乙胜. 甲说，四个球奇偶数各为两个，这个游戏对两人来说非常公平，可是乙觉得似乎不公平，请帮助乙分析，这个游戏公平吗？初中生比较喜欢玩博弈类的游戏，教师提出引导学生玩游戏，学生便对学习数学知识产生兴趣. 在学习的过程中，学生代入游戏的心情，开始认真地思考：如果自己是乙，这个游戏规则是否公平呢？应当怎么证明这个游戏规则的公正性呢？即学生在学习的过程中自主地提出了建模目标.

数学教师在开展数学建模教学时，要结合学生的生活渗透教学，让学生在生活中、游戏中遇到数学问题时，能够意识到可以用数学建模的思路解决数学问题.

2. 引导学生诠释要素

数学建模的思路，是提出一个数学问题的研究目标，然后研究数学因素之间的关系，应用描述研究目标与各个数学因素之间关系的方法，说明解决数学问题的规律，这一规律具备抽象性、可操作性、精准性. 在学生提出数学研究目标以后，部分学生不能提出数学因素之间的关系. 数学教师要在数学教学中融入数学思想的教学，引导学生找到并提出这一关系的方法.

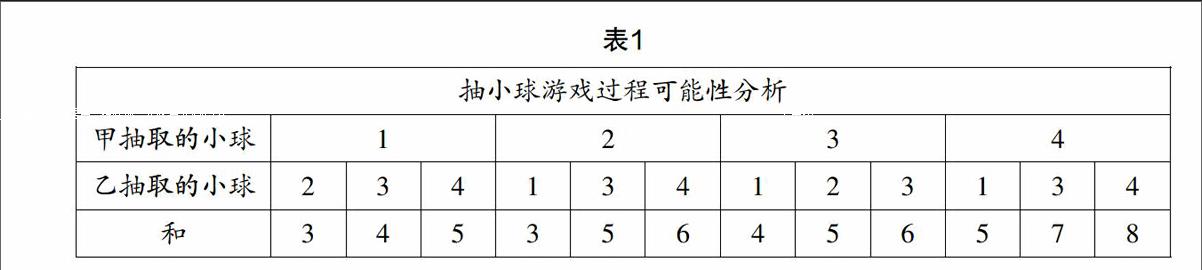
依然以教师引导学生学习《概率帮你做估计》一课为例，在学生提出数学研究的目标以后，部分学生不能理解如何分析数学因素之间的关系. 这名教师引导学生把游戏中会出现的所有情况列举出来，如表1.

教师引导学生结合表1分析，引导学生思考，看到这一张分析表，还会觉得这个游戏规则对甲、乙两人是公平的吗？学生结合这张表，能够直观地看到数学因素之间的关系. 于是数学教师可引导学生进一步思考，当数学问题较为复杂，无法寻找到数学问题之间关系的时候，可以用哪种途径找出数学因素的规律？学生通过教师的引导可理解到数学枚举法应用的意义.

初中数学教师在渗透数学模型教学时，要引导学生掌握各类数学思想，培养学生的思维能力，让学生在找到数学问题的目标后，能结合数学思想找到研究数学问题规律的切入点，建立数学模型.

3. 引导学生建立模型

当学生找到数学要素的规律以后，教师可引导学生用抽象的数学思维去思考这一规律，提出一套抽象的描述这一数学规律的方法，这套规律即数学模型. 部分学生刚开始可能不能独立地完成数学建模的过程，教师需要将综合性的数学问题转化为数个较为简单的数学问题，引导学生掌握建模的规律. 当学生受到长期的训练，抽象思维能力提高以后，便能独立思考、独立建模.

以教师引导学生学习《概率帮你做估计》一课为例，学生通过教师的引导了解到该游戏总共存在12种游戏过程，其中甲、乙手中的小球相加为奇数的结果有7个；甲、乙手中的小球相加为偶数的结果有5个. 从这一结果来分析，游戏规则倾向于甲，这一规则对乙不公平. 此时教师可引导学生思考，假如现在出现另一套规则是否公平的问题时，结合这一游戏规则的分析，应当如何解决呢？学生通过教师的引导提出：要研究事件的公平性，可将事件发生的全部过程视为1，将A事件发生的几率设为，将B事件发生的几率设为，将C事件发生的机率设为……那么该事件的发生过程模型可描述为：1=+（a，b，c均不得小于0）. 通过比较各个事件发生的几率，便可分析出事件发生的公平性.

初中数学教师可通过分解问题、逐层引导的方式引导学生建立数学模型，当学生建立了数学模型以后，教师还要引导学生提出验证模型的方法.

总结

数学模型，是指人们遇到一个数学问题以后，抽出数学问题的要点，发掘数学因素之间的内在联系，结合这套内在联系提出一个解决数学问题的规律，这一数学规律能够解决该类问题的公式. 初中数学教师要在教学中渗透数学模型思想，引导学生学会用建模的方法解决数学问题，从而提高学生解决数学问题的能力.endprint