反步轨迹跟踪控制的移动机器人队形成形控制

张文霞，袁 健

（1.青岛理工大学琴岛学院 机电工程系，青岛 266100；2.国家海洋监测设备工程技术研究中心 山东省海洋环境监测技术重点实验室 山东省科学院海洋仪器仪表研究所，青岛 266001）

多个移动机器人的队形成形控制是多机器人协调合作中的一个典型问题，比如自动化工厂中的多移动陆路机器人（AGV）协同搬运。多个移动机器人的队形成形控制可以完成单个机器人无法完成的作业任务，显著提高任务的完成效率。虚拟结构法和跟随领航者方法是当前主要采用的研究方法。文献[1-3]采用了分布式的虚拟结构编队框架实现了机器人的队形成形控制。文献[4]研究了通讯受限情况下陆地机器人的队形成形控制问题，文献[5]研究了非完整机器人的队形成形控制问题，文献[6]等研究了非完整机器人协作控制，设计了分布式控制器和估计器。但虚拟结构法要求机器人以刚体上的相应点的位置和姿态信息作为各自的跟踪目标来形成一定的队形，机器人之间存在较强的耦合关系，无法实现灵活的队形变换[1]。而跟随领航者方法要求控制1台机器人以一定的角度和距离跟踪1个或者几个机器人，能够实现编队变形或队形变换，对障碍具有好的适应性，但要求机器人间的实时通信，对角度和距离测量传感器的性能要求很高，随着距离增加通信量急剧增大。

轨迹跟踪控制方法不同于路径跟踪控制方法，其既有严格时间上的跟踪要求，又有轨迹跟踪误差上的要求[5]，可以确保在每一个规定的时刻每个机器人运动到预定的跟踪轨迹点，从而整个机器人能够形成预定的轨迹形状。本文基于backstepping轨迹跟踪控制方法提出一种多陆路移动机器人成形控制方法。首先根据多移动机器人不同的搬运任务设置不同的运动轨迹，并将设定的多个移动机器人的不同运动轨迹预编程到每个机器人控制器中，然后对每个机器人设计控制律实现对预定义轨迹的跟踪控制，这样不但简化了机器人之间的通信联系，并且可以保证每个机器人在预定的时刻跟踪上期望轨迹点，从而实现期望的控制队形。通过3次不同的运动轨迹，仿真验证了所设计控制方法的有效性。

1 移动机器人运动学模型建模

将多个移动陆路机器人协同搬运问题转化为多移动机器人的轨迹跟踪控制问题。要实现多个移动机器人的协同搬运，首先要对每个机器人的期望运动轨迹和期望运动速度进行设置，作为轨迹跟踪控制的期望轨迹和期望速度。考虑到轨迹跟踪控制对跟踪时刻和跟踪精度的要求，通过对每个机器人分别设计控制律实现对预定义轨迹的跟踪即可实现期望运动队形，如图1所示，图中实线框表示机器人的实际位置和驶向，虚线框表示机器人1的期望位置和驶向。

首先建立2个坐标系，使用栅格定位方法，分别为栅格坐标系和机器人体坐标系。移动机器人通过2个轮子驱动电机的不同转速来控制机器人的行进速度和转向，机器人的运动状态由其两驱动轮的中点在栅格平面坐标系下的位置及驶向角（即前进方向和x轴正方向的夹角）来表示。

图1 移动机器人的期望/实际位姿及误差表示方法Fig.1 Desired/true position and attitude of the mobile robots

为表示移动机器人在坐标下的位置和驶向，令p=（x，y，θ）T，q=（ν，ω）T，其中 x，y 为机器人在栅格坐标系下的位置坐标，θ为机器人的驶向角。ν，ω为控制量，分别为机器人的行驶直线速度和转向运动角速度，则移动机器人的运动学方程可以表示为

参照图1的系统期望/实际位姿及误差表示方法，进一步通过坐标系转换，机器人的运动位姿误差可以表示为

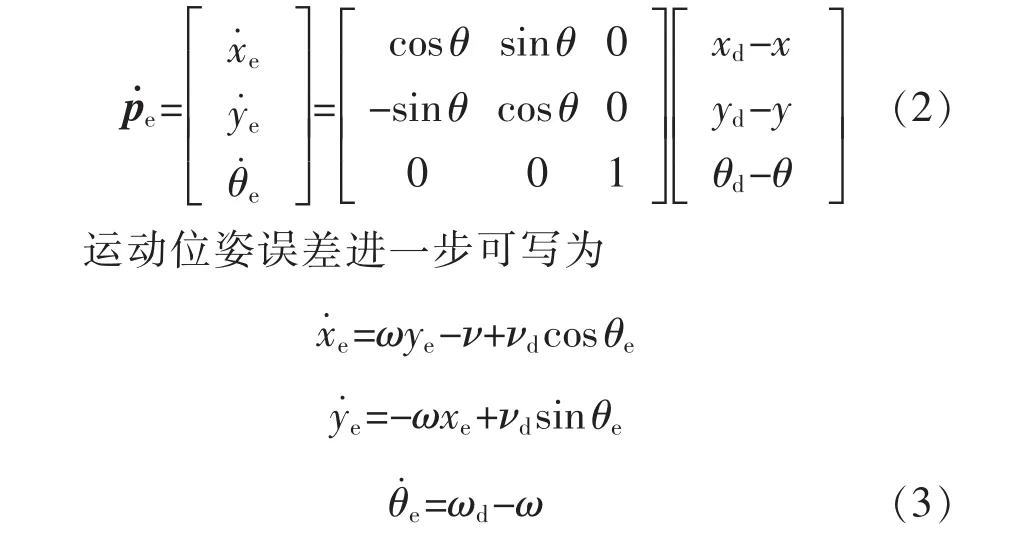
为使机器人跟踪上其预定义轨迹坐标，即使得对任意的初始位置和姿态误差（xe（0），ye（0），θe（0）），使实际移动轨迹坐标（x，y，θ）与期望轨迹坐标（xd，yd，θd）之差为零。 移动机器人的轨迹跟踪问题即通过控制机器人的直线运动速度和旋转运动速度q=（ν，ω）T，使系统误差方程（3）趋向于零，即‖（xe，ye，θe）T‖=0，并且直线运动速度和旋转运动速度ν，ω有大小限制，其中直线运动速度表示为ν=v的函数，旋转运动速度表示为的函数。

2 移动机器人反步轨迹跟踪控制器设计

设移动机器人直线运动速度ν和旋转运动速度ω可以连续变化，并且受驱动电机功率的限制有大小约束，则可以通过直线运动速度ν和旋转运动速度ω的控制律设计使得位姿系统方程式（3）对于任意的机器人初始位姿误差（xe（0），ye（0），θe（0）），随着时间的推移xe，ye和θe逐渐趋向于零，即‖（xe，ye，θe）T‖=0，这样就实现了移动机器人在预定时刻上的轨迹跟踪控制，其具体设计步骤如下：

首先令 xe=c3ωye，θe=0，则可使系统式（3）中的 ye系统趋向于零，于是可以引入一个新变量ωye，其中 c1∈R+。 对变量求导，可得：

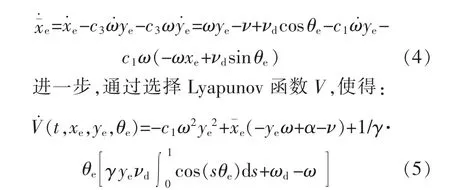
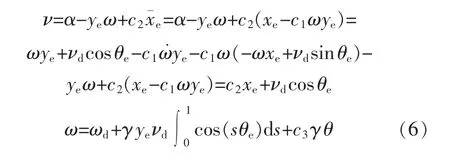
考虑到位姿系统方程式（3）的系统特性，基于反步控制律设计方法，设计的直线运动速度ν和旋转运动速度ω的控制律为

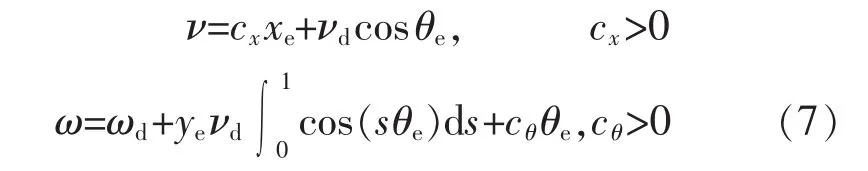
式中：cx和cθ为移动机器人控制器的轨迹跟踪收敛速度调节参数，决定着位姿误差收敛到零的速度，cx和cθ越大则机器人跟踪上期望轨迹坐标点的速度越快。使用该控制律可以使机器人跟踪上期望轨迹坐标点，实现对预定义轨迹点在预定时刻的轨迹跟踪。

3 数值仿真

要实现多个陆路移动机器人协同搬运，根据其协作操作任务性质，选择横向队形（即3个机器人平行前进）作为预期队形，期望跟踪轨迹为直线，选定工作场地内某一点为坐标原点，实现了3个移动机器人的直线轨迹跟踪控制。期望跟踪轨迹与x轴正方向的夹角分别为π/4 rad，0 rad，-π/4 rad，进行了3次队形成形仿真，3个机器人Robot1、Robot2、Robot3 的初始位置状态分别为3次仿真中机器人的位置初值保持不变，Robot1预先指定的跟踪轨迹的位置初值为Robot2预先指定的跟踪轨迹的位置初值为预先指定的跟踪轨迹的位置初值为三者间保持0.2 m的横向距离。为防止机器人打滑，将其期望角速度设置为 0，选取 ωd=0，νd=0.2 m/s，设置控制器参数为 cx=3，cθ=10，采样时间 τ=8 ms。 针对 3次不同的期望轨迹，分别进行仿真实验，期望跟踪轨迹与 x轴正方向的夹角分别为 π/4 rad，0 rad，-π/4 rad，如图2所示。图2中分别标注了3次仿真中3个机器人在200 s，500 s，700 s时的位置，其中实线表示机器人的期望运动轨迹，虚线表示机器人的真实运动轨迹，仿真表明在500 s时移动机器人基本跟踪上了期望运动轨迹并且姿态误差也收敛到0；图3为跟踪轨迹与x轴正方向的夹角为0 rad时的Robot3的位置和姿态误差，在700 s时位姿误差收敛到0，可见700 s时完全跟踪上了期望运动轨迹和姿态从而实现了比较精确的横向编队；图4为跟踪轨迹与x轴正方向的夹角为0 rad时的Robot3控制量，可以保证3个机器人以同样的运动速度和运动姿态并行前进。

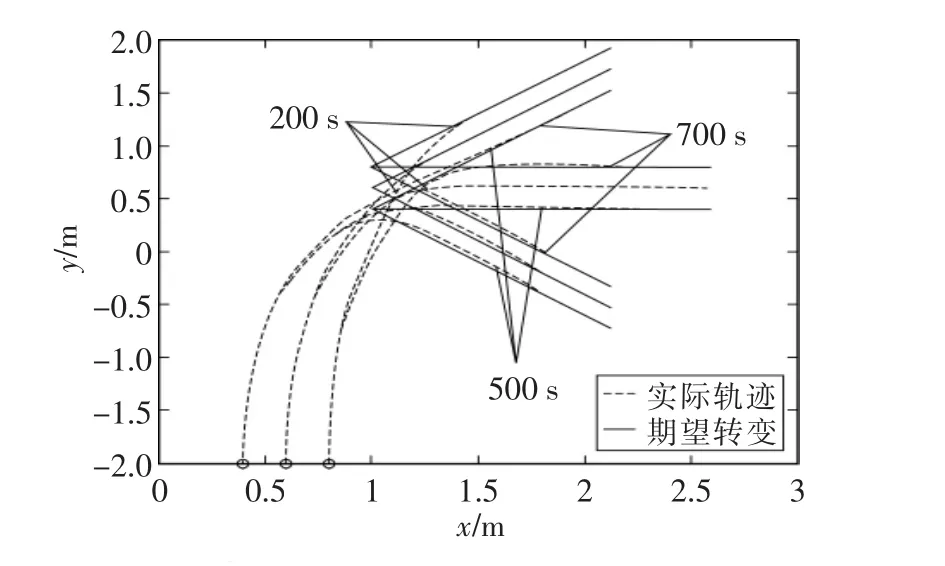
图2 轨迹跟踪控制3次运动仿真Fig.2 Three simulations for the trajectory-tracking control

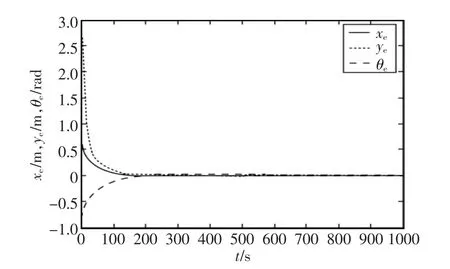
图3 跟踪轨迹与x轴正方向的夹角为0 rad时的Robot3的位姿误差Fig.3 Position and attitude error of the third robot when the angle is 0 rad between the desired trajectory and the x-axis

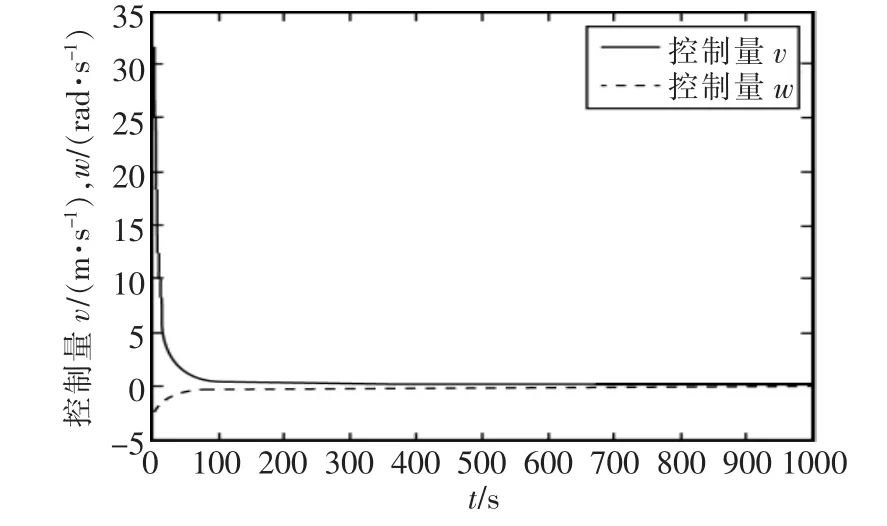
图4 跟踪轨迹与x轴正方向的夹角为0 rad时的 Robot3控制量（ν，ω）Fig.4 Control（ν，ω）of the third robot when the angle is 0 rad between the desired trajectory and the x-axis

4 结语

研究了多个陆路移动机器人队形成形控制问题。为实现机器人的在时间上的精确队形控制，设计了基于反步控制的机器人的轨迹跟踪控制方法，通过选取李雅谱诺夫函数设计了机器人的轨迹跟踪控制律，实现了多个机器人对预期轨迹的跟踪，从而形成了期望的队形。通过3个不同轨迹的仿真实验，表明所提控制方法能够形成预期队形。注意到由于控制律是渐近收敛到期望轨迹，导致过渡时间较长，研究能在有限时间内实现轨迹跟踪的控制方法是以后工作的重点。

[1]Wang P K C.Navigation strategies for multiple autonomous mobile robots moving in formation[J].Journal of Robotic Systems，1991，8（2）：177-195.

[2]Lawton J，Beard R W，Young B J.A decentralized approach to formation maneuvers[J].IEEE Trans on Robotics and Automation，2003，19（6）：933-941.

[3]Leonard N E，Fiorelli E.Virtual leader，artificial potentials and coordinated control of groups[C]//IEEE Conference on Decision and Control，2001.

[4]Ren W，Beard R W.A decentralized scheme for spacecraft formation flying via the virtual structure approach[J].AIAA Journal of Guidance，Control and Dynamics，2004，27（1）：73-82.

[5]Jiang Z P，Pomet J B.Backstepping-based adaptive controller for uncertain nonholonomic systems[C]//In Proceeding of 34th IEEE Conference on Decision and Control，New Orleans，LA，1995.

[6]Do K D.Formation tracking control of unicycle-type mobile robots with limited sensing ranges[J].IEEE Transactions on Control Systems Technology，2008，16（3）：527-538.