复合随机振动分析的混合 PC －PEM方法

第一作者 项盼 男，博士，1985年生

通信作者 赵岩 男，副教授，1974年生

邮箱：yzhao@dlut.edu.cn

复合随机振动分析的混合PC-PEM方法

项盼, 赵岩, 林家浩

(大连理工大学 运载工程与力学学部 工业装备与结构分析国家重点实验室，大连116023)

摘要：由于加工、制造等原因，实际结构系统往往所具有很多不确定性，准确评估随机系统的动力学行为不仅具有实际意义，而且是近年来结构动力学理论的一个研究热点。本文研究了同时考虑结构模型参数与所受外激励载荷具有不确定性的复合随机振动问题。结构模型参数的不确定性采用随机变量模拟，外激励载荷的不确定性采用随机过程模拟，提出了结构随机振动响应评估的混合混沌多项式-虚拟激励(PC-PEM)方法。数值算例研究了参数不确定性在21杆桁架中的传播，讨论了响应的一阶、二阶统计矩，并同蒙特卡洛方法进行对比表明提出方法的正确性和有效性。本文的工作对于考虑不确定的复杂装备与结构系统的随机振动分析具有很好的借鉴意义。

关键词：不确定;PC展开;虚拟激励法;Hermite多项式;随机伽辽金法方法

基金项目：“973”国家重点基础研究计划项目(2010CB832704)；大连理工大学理科基础科研专题(DUT12LK50)

收稿日期：2014-11-08修改稿收到日期：2014-02-25

中图分类号:O324文献标志码： A

Hybrid PC-PEM for complex random vibration analysis

XIANGPan,ZHAOYan,LINJia-hao(State Key Laboratory of Structural Analysis for Industrial Equipment, Faculty of Vehicle Engineering and Mechanics, Dalian University of Technology, Dalian 116023, China)

Abstract:Due to processing and manufacturing reasons, an actual structure system often has a lot of uncertainties. How to correctly assess dynamic behavior of an uncertain system not only has a practical significance, but also is a hot topic of structural dynamics theory in recent years. Here, the dynamic behavior of a structure with uncertain parameters under external random excitation was investigated. The uncertain parameters of the structure were taken as random variables, and the random excitations were taken as stochastic processes. The hybrid polynomial chaos and pseudo excitation method (PC-PEM) was proposed to evaluate the random vibration response of the uncertain structure. Finally, the proposed method was applied to evaluate the random response of a 21-bar truss with uncertain parameters. The first two orders statistical moments of its random response were discussed, and the correctness and effectiveness of the proposed method were verified by comparing the results of this method with those of Monte Carlo method. This study was of great significance for random vibration analysis of complex equipments and structures with uncertain parameters.

Key words: uncertainty; polynomial chaos (PC) expansion; pseudo excitation method (PEM); Hermite polynomial; random Galerkin method

由于加工、制造等一系列因素，实际工程结构模型都具有大量不确定性。对于结构响应受不确定因素的影响，近年来日益获得重视，并取得了丰硕的研究成果[1-3]。多项式混沌展开是最近二十年来发展的不确定系统动力学研究的一种有效方法，其适用于固体力学、流体力学等不同研究领域。多项式混沌展开基于概率框架以正交多项式谱展开描述随机量，对于随机微分方程结合随机伽辽金方法应用多项式混沌展开描述解和输入[4-5]。随机伽辽金方法适合于常微分方程或者偏微分方程，其基本思想是应用伽辽金投影使截断展开与耦合方程的解集误差最小，并求解获得展开系数完成不确定响应评估。Jensen等[6-7]利用多项式展开法对响应方差关于不确定参数进行展开，分析了结构在随机激励下的复合随机振动响应。Zhang[8]推导了随机场的连续正交级数展开，并与Karhunen-Loeve展开进行对比，用一阶矩法进行了结构可靠性分析。李杰[9]由次序正交分解方法建立了随机结构动力分析的扩阶系统方法，研究了随机结构在随机荷载作用下的响应变异。Schenk[10]对结构几何不确定建立了随机场，通过随机场正交分解进行了圆柱壳的屈曲分析。Qu[11]提出一个高阶数值方法用来求解具有随机系数的斯托克斯方程，对于随机输入基于有限维Karhunen-Loeve分解技术，借助随机伽辽金方法使随机斯托克斯方程转化为展开系数的确定性方程集，进一步结合块雅可比迭代技术求解该问题，并与理论结果进行了对比。

以往基于多项式混沌展开进行不确定系统分析，多数在时域上进行，讨论一条随机载荷样本。实际上，对于地震、风、路面谱等随机激励外载，由于其随机本质，由随机振动理论直接进行响应的概率统计分析更具有实际价值。对于此类问题目前还存在一定困难，如：应用随机伽辽金方法通常获得的耦合方程要远高于原系统的阶数，如果仍然按照传统随机振动理论完成功率谱等统计量分析，需要进行大量的复矩阵运算，具有高额的计算成本。本方法同时考虑结构模型参数与所受外激励载荷具有不确定性的复合随机振动问题。分别采用随机变量和随机过程模拟结构模型参数的不确定性及外激励载荷的不确定性，并基于随机伽辽金方法建立了结构随机振动响应评估的混合混沌多项式-虚拟激励法(PC-PEM)，提出的考虑不确定参数影响的虚拟响应评估代理模型有效实现了结构不确定随机响应均值和方差的准确评估。在数值算例中，研究了参数不确定性在21杆桁架中的传播，讨论了响应的一阶和二阶统计矩，并同蒙特卡洛法进行对比，表明了提出方法的正确性和有效性，本方法对于复杂结构系统双随机问题的理论分析与数值计算提供了一个可以借鉴的途径。

1多项式混沌展开的基本方法

在概率框架下多项式混沌展开以正交多项式的谱展开形式描述随机量，具有表达如下

(1)

式(1)可以简化为

(2)

式中：bi为Fourier系数，ψi(ξ(θ))是ξ(θ)(定义为高斯随机变量)的Hermite多项式排列组合乘积形式。Hermite多项式是在区间(-∞,∞)上带权exp(-α2/2)的正交多项式，其表达式为[4]

(3)

2复合随机振动分析混合PC-PEM方法

2.1不确定性分析的随机伽辽金方法

考虑不确定动力学系统控制方程的一般形式

[L(t)+Π(ξ(θ),t)]u(t)=f(t)

(4)

式中：L(t)为确定的微分算子，Π(α(θ),t)为系数具有零均值随机属性微分算子。

(5)

引入误差

(6)

如果式(6)表达的误差函数与基底函数具有正交性(也可称为投影)，也即

(7)

则利用式(7)，不确定动力学系统控制方程改写为如下形式

(8)

基于截断展开与方程解集误差最小原则，经过伽辽金投影方法可以获得一组确定性方程(见式(8))。

2.2复合随机振动分析混合PC-PEM方法

在单源随机载荷作用下，具有不确定参数系统运动方程可以表示为

(9)

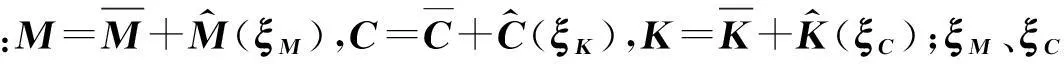
由随机有限元理论，对于质量阵、阻尼阵和刚度阵的随机部分可以表达为如下形式[6-7]

(10)

进一步，式(9)可以改写为

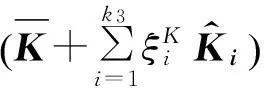
(11)

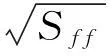
(12)

其中上标“～”代表虚拟载荷作用下的不确定虚拟响应。

由“2.1”，不确定虚拟响应的多项式混沌展开为

(13)

式中，Γj为基底多项式，aj为对应的系数向量，m为展开阶数。

将上式代入式(12)，并进行化简有

(14)

应用“2.1”节的随机伽辽金方法，同时利用Hermite多项式的正交特性，最终可获得以投影坐标为未知向量的确定性方程组集。为表达简便，采用Kronecker张量积表示为

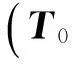
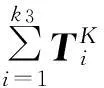
(15)

2.3复合随机振动响应统计矩评估

假定任意观测的第i个虚拟响应可表示为

(16)

这里系数aj,i已经由上小节方法计算获得；且基底多项式Γj也为已知。

由虚拟激励法，其功率谱可以表达为

(17)

随机振动功率谱均值为

(18)

式中：cj为由多项式正交性获得的常数。由式(18)可知,只要获得投影坐标的每一分量，则很容易计算随机振动功率谱均值。

进一步，随机振动功率的二阶中心矩可以表示为：

(19)

式(19)涉及多维随机变量积分，不容易给出一个显示表达式，在具体计算时可采用蒙特卡洛方法进行数值积分，由于只对观测响应，其仍具有较高的效率。

利用式(16)并结合虚拟激励法可以很容易获得随机振动功率谱等响应统计信息，所以也可称式(16)为虚拟响应评估代理模型。

3数值算例

如图1所示21杆平面桁架，结构设计参数为：水平及竖向杆长均为5 m；各杆轴向刚度均为EF=3.0×104kN；不计自重，但在所有节点上均有1 000 kg的集中质量；结构的阻尼取为瑞利阻尼。

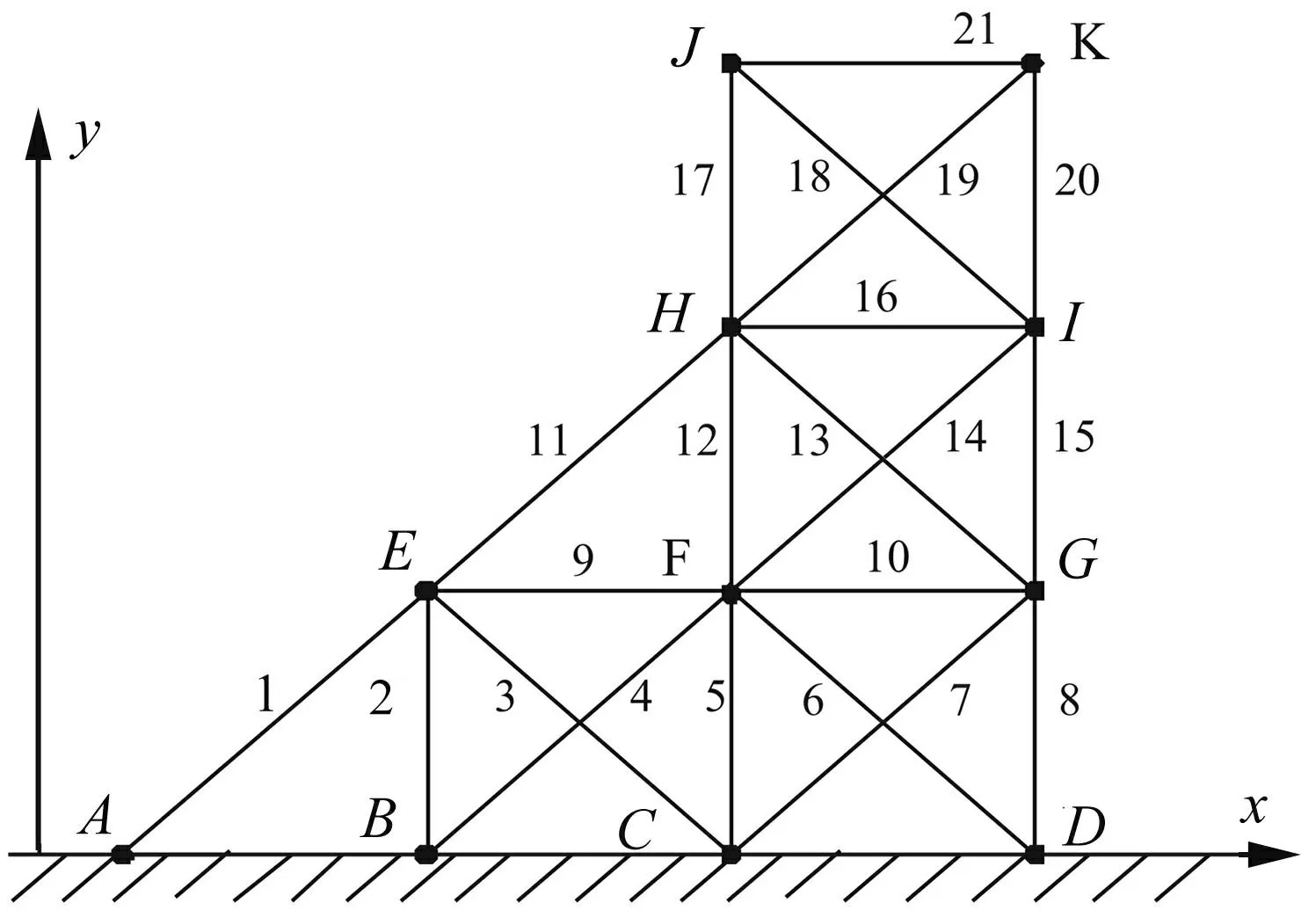
图1　平面桁架 Fig.1 Plan truss

采用沿水平x方向惯性加速度激励，采用Kanai-Tajimi谱，为

(20)

式中：ωg=15 rad·s-1和ξg=0.6分别为场地土的卓越频率和阻尼比，S0=15.74 m2·s-3为基岩地震动白噪声强度。

假定桁架某些杆件弹性模量存在不确定性，采用混合PC-PEM方法进行上述随机地震载荷下该不确定桁架系统随机振动分析。

假定具有不确定单元弹性模量的变异系数均为0.1，按照不同的观测响应与不同单元弹性模量发生变异分别进行讨论分析。工况1和工况2的观测点为J点水平方向位移，不确定单元分别为9、10、15、16、20、21和5、8、12、15、17、20。工况3和工况4的观测点为H点水平方向位移，不确定单元分别为11、12、13、16、17、20和5、8、10、15、16、21。图2～图5分别采用蒙特卡洛法(MC)和混合PC-PEM法计算了位移响应功率谱的均值和均方差，并进行了对比。为表达清楚，图2～图5采用了半对数坐标。蒙特卡洛法(MC)样本数取为1000；对于混合PC-PEM法，每一随机变量Hermite多项式取为1阶，其排列组合构成混沌正交多项式的展开项数为7阶。以图2为例可以看出，对于观测点J点水平方向位移功率谱无论是对于一阶统计矩(均值)、还是二阶统计矩(均方差)，MC法和混合PC-PEM法的计算结果都非常接近。对于图3～图5均有类似的结论。MC法对于每一样本都需要重新生成刚度矩阵，并进行动刚度矩阵的求逆运算；而混合PC-PEM法在获得随机虚拟响应的代理模型后，即可应用代理模型式(16)由式(18)和式(19)完成随机振动功率谱的统计矩分析。这里仅讨论了一阶、二阶统计矩，实际对于更高阶矩的分析也可类似完成。

图2 工况1时J点水平方向位移功率谱Fig.2ThePSDofhorizontaldisplacementresponseatnodeJforcase1图3 工况2时J点水平方向位移功率谱Fig.3ThePSDofhorizontaldisplacementresponseatnodeJforcase2图4 工况3时H点水平方向位移功率谱Fig.4ThePSDofhorizontaldisplacementresponseatnodeHforcase3

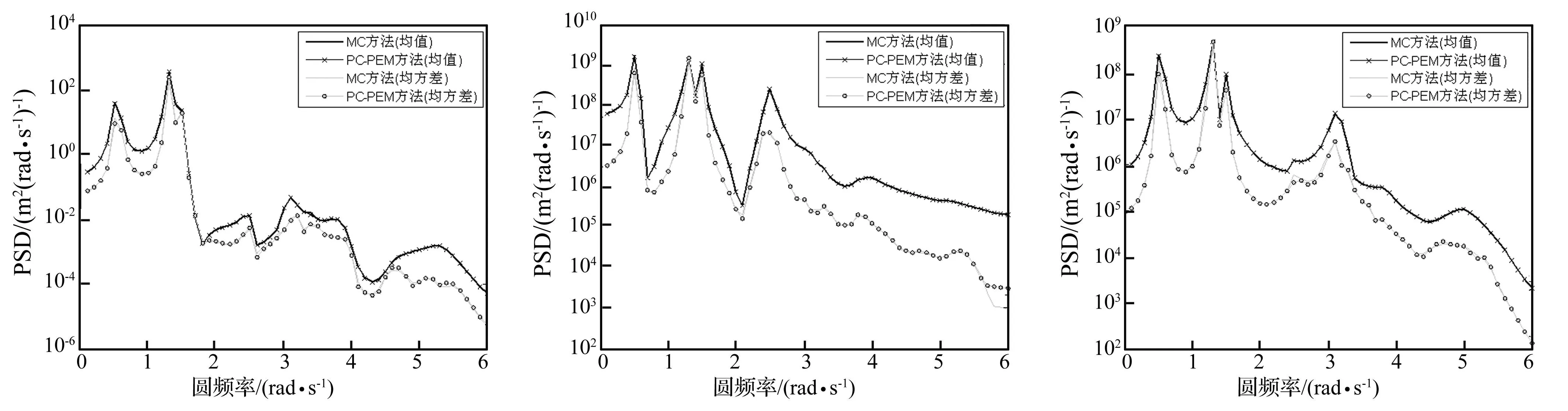
图5 工况4时H点水平方向位移功率谱Fig.5ThePSDofhorizontaldisplacementresponseatnodeHforcase4图6 第6号单元内力响应功率谱Fig.6ThePSDofinternalforceresponseforelement6图7 第9号单元内力响应功率谱Fig.7ThePSDofinternalforceresponseforelement9

另外，从图2和图3对比可知：对于工况1和工况2的功率谱均值统计量是非常一致的，但均方差统计量表现不同(图4 和图5同样有类似的结论)。对此进行了深入分析，实际上对于该算例，其不确定性系统的功率谱均值统计与确定性系统(不考虑结构具有的随机性)的功率谱相差不大，为节省篇幅，这里未列出具体对比结果图。这种现象说明了在某些情况下，由确定性系统分析作为随机系统分析的均值响应是合理的。但此时也应注意，由于系统参数不确定的传播随机振动功率谱等响应也是随机量，如考虑更可靠的不确定估计，应进行其二阶统计矩的分析，给出其可能偏离均值的范围。

图6和图7给出了考虑不确定单元为5、8、12、15、17、20，变异系数均为0.1时结构内力响应功率谱的分析结果。从图中可知采用混合PC-PEM法计算的内力功率谱响应一、二阶统计量与MC法计算结果仍具有非常好的一致性。同时也可以看出，与位移响应的计算结果相比，内力响应方差偏移均值的范围要大一些，这说明其对于不确定因素更为敏感。

4结论

研究了复合随机振动问题，不仅考虑结构参数具有的不确定性，同时考虑结构所受外激励的随机作用。基于随机有限元理论采用随机变量模拟结构模型参数的不确定性，而外激励载荷的不确定性应用随机过程进行模拟。建立了同时考虑二种不确定的混合混沌多项式-虚拟激励方法，可以有效地进行不确性传播对于随机振动功率谱等响应的影响。所取得的成果对于考虑不确定的复杂装备与结构系统的随机振动分析具有很好的实际意义。

参 考 文 献

[1] Pradlwarter H J. Relative importance of uncertain structural parameters, Part I: algorithm[J]. Computational Mechanics, 2007, 40(4): 627-635.

[2] Pellissetti M F, Pradlwarter H J, Schuéller G I. Relative importance of uncertain structural parameters, Part II: applications[J]. Computational Mechanics, 2007, 40(4): 637-649.

[3] Pradlwarter H J, Schuéller G I.Uncertain linear structural systems in dynamics: efficient stochastic reliability assessment[J]. Computers and Structures, 2010, 88(1): 74-86.

[4] Ghanem R G, Spanos P.Stochastic finite elements: a spectral approach[M]. Springer-Verlag, 1991.

[5] Knio O M, Najm H N, Ghanem R G.A stochastic projection method for fluid flow: I. basic formulation[J]. Journal of Computational Physics, 2001, 173(2): 481-511.

[6] Jensen H, Iwan H D.Response of systems with uncertain parameters to stochastic excitation[J]. Journal of Applied Mechanics, 1992, 118(5): 1012-1025.

[7] Iwan W D, Jensen H.On the dynamic response of continuous systems including model uncertainty[J]. Journal of Applied Mechanics, 1993, 60(2):484-490.

[8] Zhang J, Ellingwood B. Orthogonal series expansions of random fields in reliability analysis[J]. Journal of Engineering Mechanics, 1994, 120(12): 2660-2677.

[9] 李杰. 复合随机振动分析的扩阶系统方法[J]. 力学学报, 1996, 28(1):66-75.

LI Jie.The expanded order system method of combined radom vibration analysis[J]. Acta Mechanica Sinica,1996，28(1)： 66-75.

[10] Schenk C A, Schuéller G I. Buckling analysis of cylindrical shells with random geometric imperfections[J]. International Journal of Non-Linear Mechanics, 2003, 38(7): 1119-1132.

[11] Qu D, Xu C J.Generalized polynomial chaos decomposition and spectral methods for the stochastic stokes equations[J]. Computers & Fluids, 2013, 71(1): 250-260.

[12] 林家浩, 张亚辉. 随机振动的虚拟激励法[M]. 北京：科学出版社, 2004.