微陀螺动力学建模与非线性分析

第一作者 文永蓬 男，博士，副教授，1979月10月生

微陀螺动力学建模与非线性分析

文永蓬1，尚慧琳2

(1. 上海工程技术大学 城市轨道交通学院，上海201620； 2. 上海应用技术学院 机械工程学院，上海200235)

摘要：建立了微陀螺的动力学模型，采用多尺度方法对微陀螺的非线性模型进行求解，探讨了驱动微弹性梁和检测微弹性梁的非线性刚度对微陀螺输出的影响规律，研究了微陀螺的带宽在非线性刚度作用下的设计原则，结果表明：微陀螺振动系统的检测灵敏度和带宽呈反比关系；微弹性梁的非线性刚度会使得输入角速度与检测输出呈非线性关系。因此，从微弹性梁的设计角度出发，可根据较大的输出或者较小的非线性要求选取合适的驱动微弹性梁；而检测微弹性梁则需要选取较小的非线性刚度。

关键词：微机电系统；微陀螺；微弹性梁；非线性刚度

基金项目：国家自然科学

收稿日期：2013-12-19修改稿收到日期：2014-01-21

中图分类号:O322; TP202文献标志码： A

Dynamic modeling and nonlinear analysis for a microgyroscope

WENYong-peng1,SHANGHui-lin2(1. College of Urban Railway Transportation, Shanghai University of Engineering Science, Shanghai 201620, China; 2. School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 200235, China)

Abstract:Here, a dynamic model of a microgyroscope was built, a multi-scale method was used to solve the nonlinear model of the microgyroscope. The effects of nonlinear stiffnesses of a driving mirco elastic beam and a sensing mirco elastic beam on the output of the microgyroscope were studied. The design principles for the frequency bandwidth of the mirco-gyroscope with nonliear stiffnesses were studied. The results showed that for the vibration system of the microgyroscope, its detection sensitivity is inversely proportional to its frequency bandwidth; the input angular velocity has a nonlinear relationship with the detection output due to the nonlinear stiffnesses of mircromachined elastic beams of the microgyroscope; therefore, in the view of the design of mirco elastic beams, an appropriate driving micro elastic beam is selected according to the larger output or smaller nonlinear requirements; the sensing mirco elastic beam needs to choose a smaller nonlinear stiffness.

Key words: micro-electro-mechanical systems; mircrogyroscope; mircromachined elastic beam; nonlinear stiffness

采用微电子机械加工技术制备的振动式微陀螺是一种用来测量物体旋转角速度的传感器，其特征尺寸一般在微米级，具有体积小、重量轻、功耗低等特点，广泛应用于航空航天机载设备、状态检测以及姿态调控等方面[1-3]。

微陀螺的设计中，为了获得高性能和高稳定性，设计人员格外注重灵敏度和带宽的匹配[2]。设计新型的弹性梁用以调节驱动和检测微弹性梁的刚度是常用的一种方法[3]，它使得驱动模态和检测模态的固有频率足够接近或保持一定的距离，这样获得高灵敏度或高稳定性。无论是高灵敏度和高稳定性设计，理论上往往忽略系统的非线性影响，造成完全按照线性理论进行的测量常常不精确[4]。随着研究的深入，很多学者越来越关注微陀螺的非线性问题[5-7]。Tsai等[8]指出微陀螺的非线性能够改变系统共振频率，从而对系统的稳定性产生影响。陈志勇等[9]认为要避免或降低非线性振动对谐振器正常工作状态的影响，应尽量降低谐振器弹性特性的非线性度。李欣业等[10]考虑具有刚度非线性的微陀螺系统，对系统施加时滞位移和速度反馈控制，发现时滞反馈控制对系统动力学行为存在本质影响。上述研究里，对于微陀螺非线性振动的问题，目前还是集中在理论分析方面，讨论了非线性对系统动力学行为的影响，但所得到的研究结论尚不能直接指导设计。如何充分考虑非线性的影响从而应用到微陀螺的设计方面，尤其是非线性下的弹性梁的设计，有关的研究报道并不多。

将微陀螺的线性振动模型和考虑了非线性刚度的动力学模型进行对比分析，讨论系统带宽和灵敏度关系，研究非线性刚度作用下输入和输出的关系，从设计的角度，提出驱动微弹性梁、检测微弹性梁各自的设计要求。

1微陀螺模型和线性化分析

考虑一类典型的梳齿型振动式微陀螺[11](见图1)，该模型把微陀螺简化为具有两个自由度的刚体。这个刚体振动系统有两个相互垂直的振动模态：一个是质量块沿x方向的振动，称为驱动模态；另一个是质量块沿y方向的振动，它是科氏效应引起的谐振，称为检测模态。振动式微陀螺的工作就是将驱动模态能量转换到检测模态。由于此类微陀螺检测方向和驱动方向的阻尼均为滑膜阻尼，这里假设阻尼为线性,重点考虑非线性刚度对其振动系统动力学行为的影响。

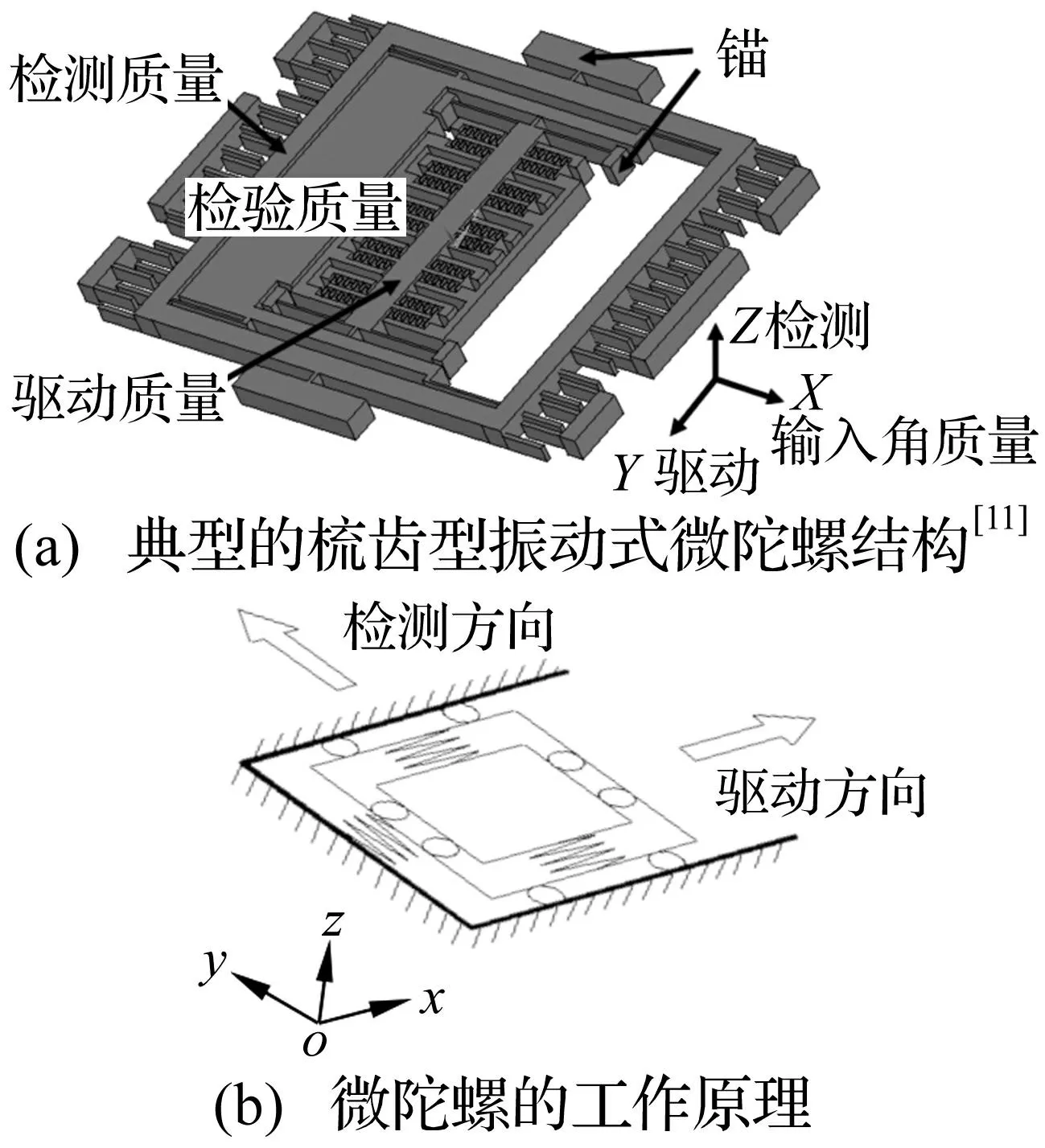
图1　微陀螺的简化动力学模型 Fig.1 A simplified dynamic model of mircrogyroscope

微陀螺工作时受x方向驱动力的作用，若外界绕x轴、y轴和z轴分别有角速度Ωx、Ωy和Ωz旋转时，微陀螺在x-y平面内的两自由度刚体计算模型的动力学方程：

(1)

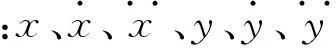
(2)

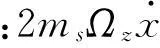
(3)

当kc=0,kq=0时，式(3)退化为线性系统：

(4)

这也是众多文献中通常采用的微陀螺分析模型[1-2,11-14]。

在小阻尼条件下，解方程(4)中的第一式，可得到驱动方向的稳态解：

x=Adsin(ω0t-ψd),

(5)

式中:

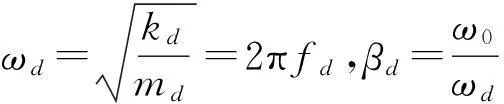
将式(5)代入线性化系统式(4)的第二式，得到检测方向的稳态解：

y=Ascos(ω0t-ψd-ψs)

(6)

式中：

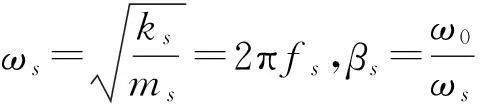
综合式(5)和式(6)，可得到线性化系统式(4)中检测方向幅值与设计参数之间的关系：

(7)

由于“灵敏度”表征的是微陀螺系统对外界输入的敏感程度，灵敏度越大表明陀螺越容易受到外界影响，通常可以用单位角速度输入引起的微陀螺在检测方向上幅值As的大小来表示灵敏度S，即：

(8)

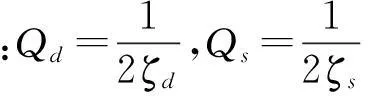
由于“带宽”是指陀螺能够精确测量输入角速度的频率范围，通常以标度因子在3 dB点处的带宽来表示，带宽越大表明陀螺的动态响应能力越强。根据带宽的定义，可以得到微陀螺的频率响应带宽表达式：

BW=0.54|ωs-ω0|

(9)

由式(9) 可知，微陀螺工作带宽BW与驱动频率ω0和检测模态固有频率ωs的匹配相关，与驱动频率ω0和驱动模态的固有频率ωd的匹配无关。但是，为了要获得较大的驱动响应和检测响应，驱动频率ω0一般取ωd。

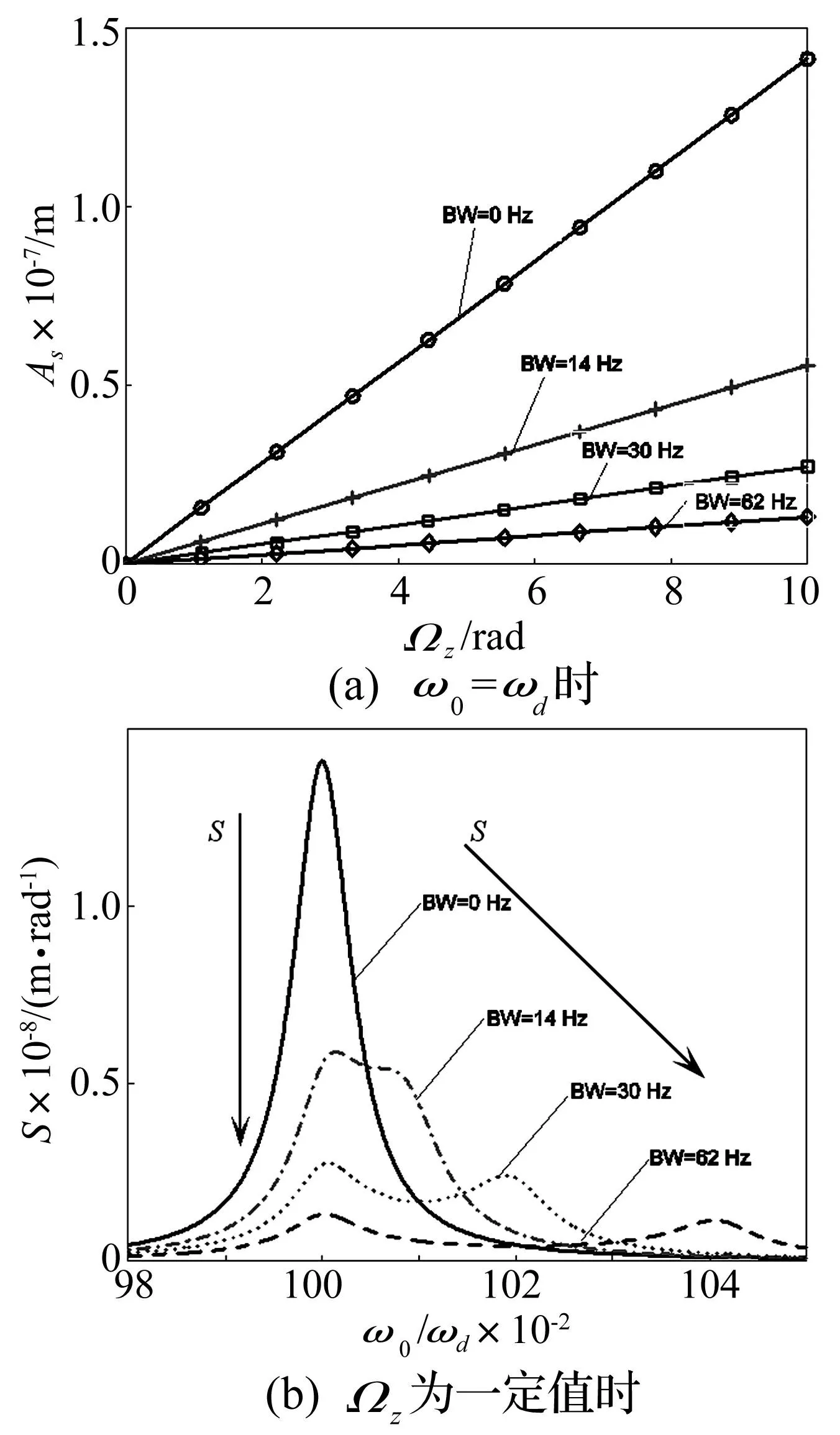
图2　微陀螺带宽BW与灵敏度S的关系图 Fig.2 Relationship between bandwidth and sensitivity of micro gyroscope

不计刚度非线性的情况下，微陀螺带宽BW与灵敏度S的关系见图2。由图2 (a)可知，外界激励驱动频率ω0取ωd时，外界输入角速度Ωz与检测位移幅值As呈线性关系，该曲线的斜率即为灵敏度，随着带宽BW的增大，灵敏度下降。由图2 (b)可知，外界输入角速度Ωz为定值，当驱动模态固有频率ωd与检测模态固有频率ωs不相等时，在频域上有两个峰值，当驱动频率ω0等于驱动模态固有频率ωd或检测模态固有频率ωs时，灵敏度较大；当驱动模态固有频率ωd与检测模态固有频率ωs相等时，在频域上仅有一个峰值，灵敏度最高，但此时带宽为0；带宽BW从0、30 Hz、46 Hz增宽到62 Hz，灵敏度S在检测模态和驱动模态分别都降低。因此，可以认为带宽与灵敏度成反比关系，微陀螺要同时具有高灵敏度和高稳定性，它的驱动模态固有频率ωd和检测模态固有频率ωs必须有偏差。

在驱动模态固有频率ωd和检测模态固有频率ωs偏差相等时，同时增大阻尼时，线性系统式(4)的幅频特性见图3。由图3可知，无论如何改变系统阻尼，均不影响带宽BW，随着驱动模态和检测模态的阻尼增大，驱动模态和检测模态处同时灵敏度减小，当增大到某值时，驱动模态和检测模态处的灵敏减小到几乎相等，虽然能获得大带宽，但灵敏度几乎为0，系统对外界输入响应过低，并且，检测模态cs的阻尼增大的倍数较驱动模态的阻尼cd小时，检测模态处灵敏度减小的速度会较驱动模态处灵敏度减小的速度慢。因此，在固定带宽下的灵敏度设计中，应尽可能的减小驱动模态的阻尼cd和检测模态的阻尼cs，尤其需要减小检测模态的阻尼cs

图3　阻尼的改变对灵敏度S的 影响关系图(BW=30 Hz) Fig.3 The damping effect on the sensitivity with BW=30 Hz

2模型的非线性分析

在考虑微陀螺的刚度非线性时，考察系统式(3)。首先将系统式(3)进行无量纲化，设

则系统式(3)成为

(10)

为得到系统式(10)的近似周期响应，可运用多尺度法，设

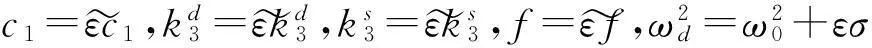
T0=t,T1=εt,…,

x(t,ε)=X0(T0,T1)+εX1(T0,T1)+O(ε2),

则式(10)的第1式成为

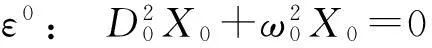
(11)

因此，

(12)

代入式(11)，比较长期项eiω0T0的系数得到：

(13)

令等式(13)右端为0，则可以求解A和φ。由此可知

x(t,ε)≈Acos(ω0t+φ)

(14)

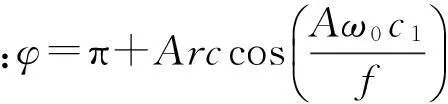
(15)

将式(14) 代入式(10)的第二式得到

由于A=A(T1),因此仍可以设

同理得到：

(16)

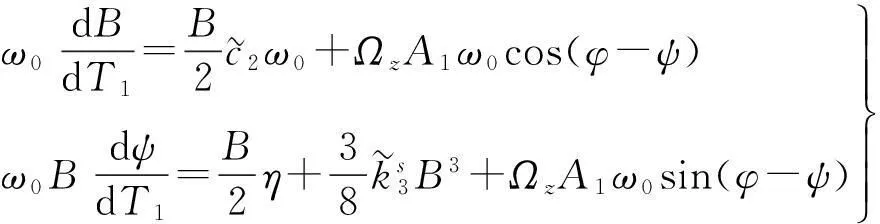
令等式(17)右端为0，则得到检测方向的周期解

y≈-Bsin(ω0T0+ψ)

(18)

(19)

根据式(15)和(19)，检测振幅B为Ωz的非线性函数，其非线性程度取决于检测刚度非线性系数kq和驱动刚度非线性系数kc。

由于系统检测方向的弹性力为

F=ksy+kqy3=(ks+kqy2)y

(20)

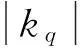
外界输入角速度Ωz随检测位移幅值B的变化见图4，二者之间不再呈线性关系，造成按照线性理论计算出的角速度不够精确，同时系统的灵敏度不再是一固定值，而是随着Ωz的变大逐渐变小 。

随着驱动微弹性刚度非线性系数kc的增大，检测振幅B下降，并且其非线性程度下降。kc取值在[1,1010]的范围内, 检测振幅B受到影响的较小。因此，驱动微弹性非线性刚度对检测振幅的耦合影响比较低，设计微陀螺的驱动微弹性梁时，可以选取驱动微弹性非线性刚度较大的微弹性梁，这样会获得较大的系统输出响应，或者选取驱动微弹性非线性项较小的微弹性梁，尽管响应偏小但是这样可以获得趋于线性的系统输出。

同时，随着检测刚度非线性系数kq的增大，检测振幅B下降，并且其非线性程度升高(见图5)。因此，设计微陀螺的弹性梁时，从获得较大的系统输出响应以及线性输出的角度考虑这两个方面考虑，都应该尽量避免检测微弹性梁较大的刚度非线性，尤其是要确保检测位移不要超过弹性范围，这与非线性刚度作用下驱动微弹性梁的设计是不同的。

图4 当ω0=ωd,BW=62,kq=1016时,系统输出随驱动梁刚度非线性系数kc的变化Fig.4Theoutputofthesystemvarieswithkcwhenω0=ωd,BW=62,andkq=1016图5 当ω0=ωd,BW=62,kc=1时,系统输出随检测梁刚度非线性系数kq的变化Fig.5Theoutputofthesystemvarieswithkqwhenω0=ωd,BW=62,andkc=1图6 当ω0=ωd,kc=1,kq=1016时,系统输出随带宽的变化Fig.6Theoutputofthesystemvarieswithbandwidthwhenω0=ωd,kc=1,andkq=1016

而根据带宽对系统式(3)的输出的影响规律发现，与线性系统类似，随着带宽的增大，灵敏度下降(见图6)。根据图6，系统的灵敏度和输入角度速度呈非线性关系，当Ωz=0.1时，零带宽的输出明显高于有一定带宽值的输出，这说明非线性刚度会造成在零角速度附近系统相对大的输出，即出现明显的零点漂移，这非常不利于检测。因此，在设计微陀螺带宽的时候，虽然零带宽会带来较高的输出，但是，从非线性刚度对系统的影响角度看，应该尽量避免零带宽，一般选取一定的带宽以便减少零点漂移，提高系统测量精度。

3结论与讨论

针对一类典型的梳齿型振动式微陀螺，通过建立微陀螺的线性和非线性振动模型，对比线性模型和非线性模型的系统输出和输入之间的关系，获得如下结论：

(1) 无论线性模型还是非线性模型，微陀螺振动系统的检测灵敏度和带宽都呈反比关系；

(2) 微弹性梁的非线性刚度使输入角速度与检测输出呈非线性关系，检测微弹性梁刚度的非线性系数在1016数量级时，系统的非线性程度明显增强，因此，为了精确测量的要求，必须考虑系统的非线性。

(3) 从微弹性梁的设计角度来看，驱动微弹性非线性刚度对检测振幅的耦合影响比较低，可根据较大的输出或者较小的非线性需要选取合适的驱动微弹性梁；而检测微弹性梁则需要选取较小的非线性刚度，确保检测位移不要超过弹性范围。

考虑到微弹性梁的非线性刚度的影响，为了减小零点漂移，微陀螺的带宽必须非零。这有别与以往在高灵敏度设计方面的一些认知，这一点是令人感兴趣的。此外，微机械陀螺的工作环境常置于空气中，由此空气阻尼中的压膜阻尼和滑膜阻尼引起的非线性效应也是影响器件动态性能和稳定性的重要因素。讨论不同拓扑结构下的微机械陀螺的非线性阻尼对陀螺灵敏度和稳定性方面的影响，以及阻尼非线性和刚度非线性以及非线性静电力等因素对微陀螺谐振系统的动力学行为的耦合作用，将成为我们下一步的工作目标。

参 考 文 献

[1] 王喆垚. 微系统设计与制造 [M]. 北京:清华大学出版社，2008.

[2] Bao Min-hang. Analysis and design principles of MEMS devices [M]. Holland: Elsevier press, 2005.

[3] 文永蓬, 王安麟, 姜涛, 等. 音叉振动式微机械陀螺弹性梁的研究 [J]. 高技术通讯, 2008, 18(12):1274-1279.

WEN Yong-peng, WANG An-lin, JIANG Tao,et al. Study on tuning fork vibratory microgyroscope spring beams[J]. Chinese High Technology Letters, 2008, 18(12):1274-1279.

[4] Francesco B, Ferruccio R. Nonlinear dynamics of vibrating MEMS[J]. Sensors and Actuators A, 2007, 134: 98-108.

[5] 孟光, 张文明. 微机电系统动力学 [M]. 北京:科学出版社, 2008.

[6] 尚慧琳, 文永蓬.一类静电驱动微结构谐振传感器的吸合不稳定性研究及控制[J]. 振动与冲击, 2013, 32(15):8-13.

SHANG Hui-lin, WEN Yong-peng. Pull-in stability of electrostatically actuated MEMS resonant sensor and its control [J]. Journal of vibration and shock,2013, 32(15):8-13.

[7] 尚慧琳, 文永蓬. 软弹簧Duffing 系统的安全盆侵蚀及其时滞位移反馈控制[J]. 振动与冲击, 2012, 31 (8):11-15.

SHANG Hui-lin, WEN Yong-peng. Erosion of safe basins in a softening duffing system and its control with time-delay position feedback [J]. Journal of Vibration and Shock, 2012, 31 (8):11-15.

[8] Tsai N C, Sue C Y. Stability and resonance of micro-machined gyroscope under nonlinearity effects [J]. Nonlinear Dynamics, 2009, 56:369-379.

[9] 陈志勇,周斌,张嵘.微机械角振动谐振器在低气压下的非线性振动[J].仪器仪表学报, 2010, 31(11):2481-2487.

CHEN Zhi-yong, ZHOU Bin, ZHANG Rong. Nonlinear vibration ofm icromachined angular vibration resonator [J]. Chinese Journal of Scientific Instrument, 2010, 31(11):2481-2487.

[10] 李欣业,张利娟,张华彪.陀螺系统的受迫振动及其时滞反馈控制 [J]. 振动与冲击, 2012, 31(9):63-68.

LI Xin-ye, ZHANG Li-juan, ZHANG Hua-biao.Forcedvibration of a gyroscope system and its delayed feedback control [J]. Journal of Vibration and Shock, 2012, 31(9):63-68.

[11] Liu X S, Yang Z C, Chi X Z, et al. A doubly decoupled lateral axis micromachined gyroscope[J].Sensors and Actuators A: Physical, 2009，154(2):218-223.

[12] 陈永. 基于滑膜阻尼效应的音叉式微机械陀螺研究[D]. 上海：中国科学院上海微系统与信息技术研究所, 2004.

[13] Said E A, Kanber M S, Tayfun A. A low-cost rate-grade nickel microgyroscope[J]. Sensors and Actuators A, 2006, 132:171-181.