多管火箭总传递方程自动推导和动力学可视化仿真方法研究

第一作者 辛松 女，助理研究员，1980年生

通信作者 芮筱亭 男，博士, 教授, 博士生导师，1956年生

邮箱:ruixt@163.net

多管火箭总传递方程自动推导和动力学可视化仿真方法研究

辛松, 芮筱亭, 芮雪, 张建书, 王国平

(南京理工大学 发射动力学研究所，南京210094)

摘要：多管火箭系统总传递方程的自动推导和动力学快速计算是多管火箭系统动力学设计的关键。针对某新型多管火箭，建立多管火箭多体系统发射动力学模型及其拓扑结构，根据符号约定和各元件传递方程，建立了某多管火箭系统总传递方程自动推导方法，提高了多管火箭多体系统建模效率和程式化水平。建立了多管火箭系统动力学可视化仿真系统，实现了新型多管火箭动力学快速可视化仿真，并得到了试验验证。为新型多管火箭动力学设计提供了理论基础。

关键词：新型多管火箭；多体系统传递矩阵法；总传递方程；可视化仿真

基金项目：高校博士点基金(20113219110025);国家自然科学基金(11102089,11472135);国防基础科研计划资助(B2620132013);新世纪优秀人才支持计划资助(NCET-10-0075)

收稿日期：2014-03-12修改稿收到日期：2014-06-17

中图分类号:TB122;TB124文献标志码： A

Automatic deduction for overall transfer equation of a multiple launch rocket system and its dynamic visual simulation method

XINSong,RUIXiao-ting,RUIXue,ZHANGJian-shu,WANGGuo-ping(Research Institute of Launch Dynamics, Nanjing University of Science & Technology, Nanjing 210094, China)

Abstract:Automatic deduction of overall transfer equation and dynamic rapid simulation for a multiple launch rocket system (MLRS) are the key to its dynamic design. Here, a new type MLRS, its multibody system launch dynamic model and topological structure were built. According to sign conventions and transfer equations of elements, an automatic method to deduce the overall transfer equation of the new type MLRS was proposed. Its modeling efficiency and programming level were improved. A dynamic visual simulation system for the new type MLRS was established, its launch dynamic behavior was simulated rapidly and validated with tests. The results provided a theoretic foundation for the dynamic design of the new type MLRS.

Key words: new type multiple launch rocket system; transfer matrix method for multibody systems; overall transfer equation; visual simulation

多管火箭系统动态设计是提高多管火箭研制和试验水平的前提和基础。新型多管火箭动态设计，急需解决多管火箭动力学快速计算难题[1,3,6]。芮筱亭等通过建立多体系统传递矩阵法[7-9]，为多管火箭动力学快速计算和动态设计提供了强有力的工具[2,4-5]。作为一种多体系统动力学新方法，多体系统传递矩阵法由于其多体系统动力学分析无需系统总体动力学方程、涉及矩阵阶次低、计算速度快的特点，被广泛用于各种多管火箭、自行火炮、舰炮等复杂大型机械系统动力学分析与设计。

针对某新型多管火箭的特点，建立了多管火箭多体系统发射动力学模型及其拓扑结构，根据符号约定和各元件传递方程，建立了某多管火箭系统总传递方程自动推导方法，提高了某多管火箭多体系统建模效率和程式化水平。建立了多管火箭系统动力学可视化仿真系统，实现了新型多管火箭动力学快速可视化仿真，并得到了试验验证。提高了新型多管火箭动力学研究的程式化，为新型多管火箭动力学设计提供了理论基础。

1新型多管火箭多体系统发射动力学模型

应用多体系统传递矩阵法，建立某多管火箭系统动力学模型(见图1)。根据新型多管火箭各部件的自然属性，将它们分别视为集中质量、刚体、弹性梁、扭簧、弹簧等力学元件，并依次编号；这些元件分为“体”和“铰”两大类，“体”指集中质量、刚体、弹性梁，而“铰”泛指任何“体”与“体”之间的线位移、角位移、力、力矩联接关系，包括光滑铰、弹性铰、滑移铰、阻尼器。

图1　某新型多管火箭多体系统动力学模型 Fig.1 Multibody system dynamics modal of an new type multiple launch rocket system

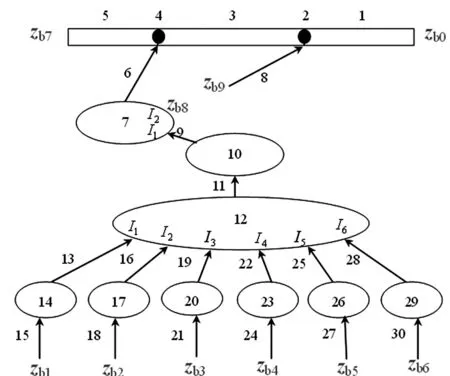
图2　新型多管火箭动力学模型拓扑 Fig.2 Topological graph of dynamics modal of the new type multiple launch rocket system

该新型多管火箭拓扑结构见图2。

体元件标号14、17、20、23、26、29为车轮，12为车体，10为回转部分，7为俯仰部分，3和1为定向管部分，5为定向管尾部；6为铰元件标号、8为联接定向管与俯仰部分的铰元件，9为联接回转部分与俯仰部分的铰元件，11为联接车体和回转部分的铰元件，13、16、19、22、25、28为联接车轮与车体的铰元件，15、18、21、24、27、30为联接地面与车轮的铰元件。系统中共有8个边界点：其中，zb0为定向管前部自由端，zb7为定向管尾部自由端，zb1、zb2、zb3、zb4、zb5、zb6为铰元件15、18、21、24、27、30与地面相固联端。将边界zb0视为系统的树根，其他边界zb1、zb2、zb3、zb4、zb5、zb6、zb7、zb8、zb9视为系统的树梢，整个树形系统的传递方向为从树梢指向树根。箭头的指向与整个系统的传递方向一致。用Ik(k=1,2,…,L)对不同的输入点进行标号，其中L为元件输入点个数。

2新型多管火箭元件和系统传递方程

根据新型多管火箭多体系统动力学模型，建立新型多管火箭多体系统数学模型——多管火箭多体系统动力学方程。

根据多体系统传递矩阵法定义各联接点或边界点的状态矢量为ZP，对于刚性体元件，有

zP=[xyzθxθyθzmx

mymzqxqyqz1]TP

(1)

对于柔性体元件，有

zP=[xyzθxθyθzmxmy

mzqxqyqzq1q2…qn1]TP

(2)

式中：x,y,z为该点相对于空间惯性坐标系的位置坐标；θx,θy,θz为相对于空间惯性坐标系的空间三轴角；mx,my,mz为系统在该点处的内力矩；qx,qy,qz为系统在该点处的内力。q1，q2，…，qn为用假设模态法描述的变形体的广义坐标，n该广义坐标的最高阶数。

对含有多个端点的任意元件j的传递方程和几何方程分别为

zj,O=Uj,I1zj,I1+Uj,I2zj,I2…+Uj,ILzj,IL

(3)

和

Hj,IKzj,IK=Hj,I1zj,I1

(k=2,…,L)

(4)

单端输入单端输出元件的传递方程为

zj,O=Uj,I1zj,I1

(5)

2.1多端输入单端输出空间运动刚体的传递方程与几何方程

对多端输入单端输出空间运动刚体(见图3)。式(3)为传递方程，式(4)为不同输入点之间的几何方程形式，其中各矩阵的形式为：

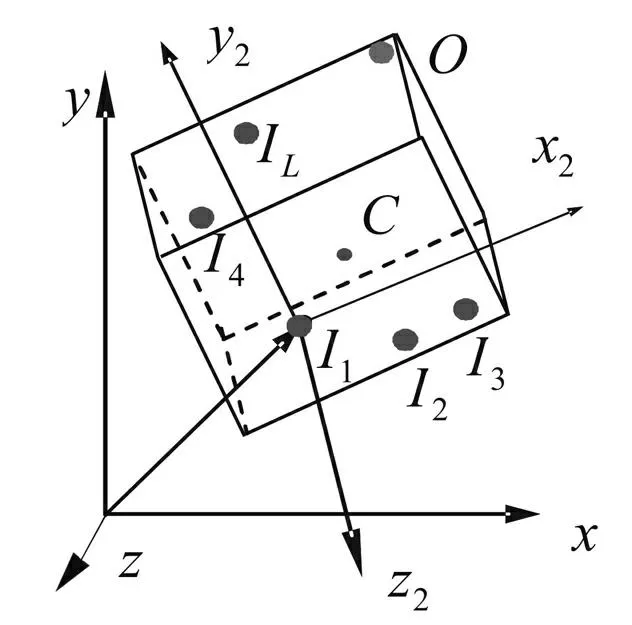
图3　多端输入单端输出空间运动刚体 Fig.3 Multi-input and single-output rigid body moving in space

(6)

(k=2,…,L)

(7)

(8)

(k=2,…,L)

(9)

式中各符号含义参见文献[1]。

2.2单端输入单端输出空间运动梁的传递方程与几何方程

对于单端输入单端输出空间运动梁。式(5)为传递方程的形式，单端输入单端输出空间运动梁无需几何方程。其矩阵的形式为:

(10)

式中各符号含义参见文献[1]。

3新型多管火箭多体系统总传递方程和总传递矩阵

根据多体系统总传递方程自动推导方法[10]和新型多管火箭动力学模型拓扑图，可自动推导获得多管火箭的总传递方程

Uallzall=0

(11)

和系统总传递矩阵

(12)

式中

(13)

(14)

(15)

(16)

(17)

(18)

(19)

并注意：

(1) 总传递方程只涉及系统边界状态矢量。

(2) 总传递矩阵第一行中的子矩阵分别为各传递路径中各元件传递矩阵依次连乘积。

(3) 总传递矩阵中的其它子矩阵为由从边界点到分叉体元件的输入点路径上各个元件的传递矩阵的连乘积。

4新型多管火箭动力学可视化仿真

基于多体系统传递矩阵法，芮筱亭团队首次研发了具有自主知识产权的多管火箭系统动力学可视化仿真软件——MLRSDynSim，该软件具有多管火箭系统动力学快速计算、CAD文件直接调用、计算参数和计算结果自动生成、数据分析处理和动力学过程可视化等功能。应用建立的MLRSDynSim，实现了某新型多管火箭可视化动力学仿真和设计，包括：创建多管火箭三维实体模型、多体系统动力学模型，计算并动画、曲线、图表显示多管火箭系统振动特性、动力响应、起始扰动、发射与飞行动力学过程、射击精度。

多管火箭系统动力学可视化仿真系统架构见图4，图5为系统参数输入界面，图6为可视化仿真曲线显示界面。

图4　多管火箭系统动力学可视化仿真系统架构图 Fig.4 The architecture of visual dynamics software for MLRS

图5　系统参数输入界面 Fig.5 The input interface for system parameters

图6　可视化仿真曲线显示界面 Fig.6 The display interface for visual simulation curve

5新型多管火箭动力学快速仿真及试验验证

根据建立的新型多管火箭多体系统传递方程和传递矩阵，结合火箭弹发射动力学方程，建立了新型多管火箭发射动力学仿真系统，实现了新型多管火箭动力学的快速仿真，仿真获得了新型多管火箭动力响应、火箭弹膛内运动、火箭弹发射与飞行动力学等动态特性。图7和图8分别给出了新型多管火箭发射过程中定向管口Y方向(垂向)和Z方向(侧向)的位移时间历程。

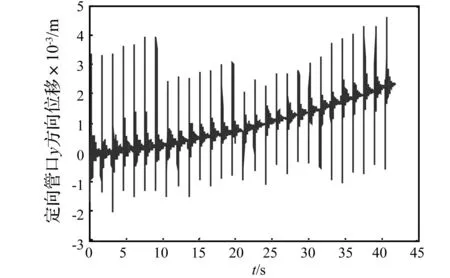
图7　新型多管火箭定向管口Y方向位移 Fig.7　The displacement in Y direction of the tip of the tube of the new type multiple launch rocket system

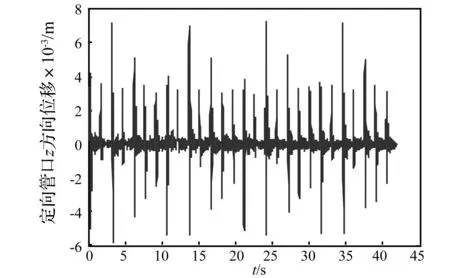
图8　新型多管火箭定向管口Z方向位移 Fig.8　The displacement in Y direction of the tip of the tube of the new type multiple launch rocket system

5.1新型多管火箭弹出炮口弹道参数仿真结果及试验验证

表1给出了某新型多管火箭弹出炮口弹道参数仿真与试验测试结果的对比，两者吻合，验证了多管火箭总传递方程自动推导方法和仿真系统的可信度。

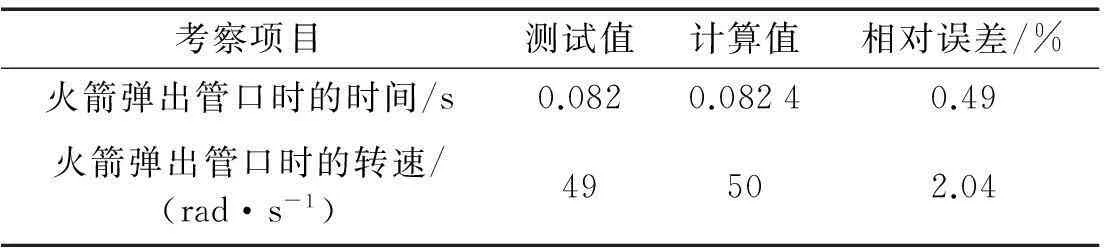
表1　某新型多管火箭弹出炮口参数测试与仿真结果

5.2新型多管火箭弹主动段末弹道参数仿真结果及试验验证

表2给出了某新型多管火箭弹主动段末参数仿真与测试结果的对比，两者吻合较好，进一步验证了多管火箭总传递方程自动推导方法和仿真系统的可信度。

表2　某新型多管火箭弹主动段末参数弹道计算与测试结果

6结论

针对某新型多管火箭，建立多管火箭多体系统发射动力学模型及其拓扑结构，根据符号约定和各元件传递方程，建立了某多管火箭系统总传递方程自动推导方法，提高了多管火箭多体系统建模效率和程式化水平。编制了多管火箭系统动力学可视化仿真软件，实现了新型多管火箭动力学快速可视化仿真，并得到了试验验证，提高了新型多管火箭动力学研究的程式化。为新型多管火箭动态设计提供了理论支撑。

参 考 文 献

[1] 芮筱亭, 贠来峰, 陆毓琪,等. 多体系统传递矩阵法及其应用[M]. 北京: 科学出版社, 2008.

[2] 芮筱亭, 陆毓琪, 王国平, 等. 多管火箭发射动力学仿真与试验测试方法[M]. 北京: 国防工业出版社, 2003.

[3] 芮筱亭, 贠来峰, 陆毓琪,等. 多管火箭发射动力学研究[J]. 兵工学报,2004, 25(5): 556-561.

RUI Xiao-ting, YUN Lai-feng, LU Yuqi, et al. A study on the launch dynamics of multiple launch rocket system[J]. Acta Armamen Tarii, 2004, 25(5): 556-561.

[4] 芮筱亭, 王国平, 陆毓琪. 提高多管火箭射击密集度新技术[J]. 兵工学报, 2006, 27(2): 301-305.

RUI Xiao-ting, WANG Guo-ping, LU Yuqi, et al. A new technology to improving firing dispersion of multiple launch rocket system[J]. Acta Armamen Tarii, 2006, 27(2): 301-305.

[5] 展志焕, 芮筱亭, 王国平, 等. 基于多体系统传递矩阵法的多管火箭定向器振动控制. [J] 力学学报, 2010, 42(3): 583-590.

ZHAN zhi-huan,RUI Xiao-ting, WANG Guo-ping, et al. Vibration control for launcher of multiplelaunch rocket system based on transfer matrix method of multibody system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3):583-590.

[6] Rui Xiao-ting, Wang Guo-ping, Lu Yuqi, et al. Transfer matrix method for linear multibody system[J]. Multibody System Dynamics, 2008, 19(3): 179-207.

[7] Rui X T, He B, Rong B, et al. Discrete time transfer matrix method for multi-rigid-flexible-body system moving in plane[J]. Journal of Multi-Body Dynamics, 2009, 223(S1): 23-42.

[8] Rong B, Rui X T, Wang G P, et al. New efficient method for dynamics modeling and simulation of flexible multibody systems moving in plane[J]. Multibody Syst. Dyn., 2010, 24(2): 181-200.

[9] Rong B, Rui X T, Wang G P, et al. Discrete time transfer matrix method for dynamic modeling of complex spacecraft with flexible appendages[J]. Journal of Computational and Nonlinear Dynamics, 2011, 6(1): 011013.

[10] Rui Xiao-ting, Zhang Jian-shu, Zhou Qin-bo. Automatic deduction theorem of overall transfer equation of multibody system[J]. Advance in Mechanical Engineering, Volume 2014, Article ID 378047,12Pages,.doi.org/10.1155/2014/378047.