非轴对称多元载荷条件下管道中纵向模态导波激励

第一作者 马书义 男，博士，1980年生

通信作者 武湛君 男，博士后，教授，博士生导师，1970年生

非轴对称多元载荷条件下管道中纵向模态导波激励

马书义，武湛君，刘科海，王奕首

(大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连116024)

摘要：轴对称载荷是管道中轴对称模态导波激励的有效方法。然而，受换能器安装误差等因素的影响，激励载荷多会变为非轴对称载荷，进而使激励出的导波模态变得复杂。对非轴对称多元载荷条件下纵向模态导波的激励问题进行了深入研究。考虑两种典型的非轴对称载荷，采用简正模态展开技术，建立了导波激励声场与边界载荷的量化关系，进而分析了各模态导波的产生机理及载荷阵列对纵向导波激励的影响。采用有限元数值模拟验证了理论预测结果。考虑实际管道检测中出现的非轴对称载荷，提出了一种载荷补偿策略并进行了实验验证。结果表明，该方法能够有效抑制弯曲模态导波的产生，同时也有助于改善导波信号的噪声水平。

关键词：非轴对称载荷；纵向模态；导波激励；载荷补偿

基金项目：国家科技重大专项(2008ZX05026);国家自然科学基金(91016024);教育部新世纪人才(NCET-11-0055);中央高校基本科研业务费(DUT12LK33)

收稿日期：2013-09-30修改稿收到日期：2014-02-20

中图分类号:O348.8文献标志码： A

Longitudinal guided waves in pipes excited by non-axisymmetric multielement surface loading

MAShu-yi,WUZhan-jun,LIUKe-hai,WANGYi-shou(State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China)

Abstract:Axisymmetric surface loading is an effective method to excite axisymmetric guided waves in pipes. However, non-axisymmetric surface loading appears due to various influence factors, such as, transducer installation error and it leads to the complex excited guided wave modes. Here, longitudinal guided waves excited by non-axisymmetric multielement surface loading were investigated deeply. Two typical non-axisymmetric loadings were considered and analyzed. Based on the normal modal expansion technology, the quantitative relationship between applied boundary loadings and guided wave excitation acoustic field was built, and then the generation mechanism of individual guided wave was analyzed and the effects of non-axisymmetric loading array on the generation of longitudinal guided wave were studied. Theoretical predictions were verified with the finite element simulations. For the non-axisymmetric surface loading occurring in the actual pipe inspection, a new loading compensation strategy was proposed and verified with tests. The results showed that the compensation strategy can suppress the flexural modes effectively, and is helpful to improving the noise level of guided wave signals.

Key words: non-axisymmetric surface loading; longitudinal mode; guided wave excited; loading compensation

超声导波管道检测是一种具有潜在吸引力的新兴无损检测技术[1-3]。该技术采用脉冲-回波原理,通过在管道一处布置换能器阵列即可实现几十米范围内管道的全局检测，效率高，成本低。鉴于导波技术用于管道检测的优势，其相关问题的研究亦得到了快速的发展且正逐步深入。

根据管道实际检测需要，选择合适的导波模态并高效激励期望模态导波是管道导波检测研究的关键问题之一。在导波的众多模态中，低阶的轴对称模态导波由于声场简单，易在管道中激励而受到了广大学者的关注。轴对称模态导波激励要求换能器阵列对管道施加轴对称载荷。目前，基于不同载荷施加方式的导波激励方法及相应的换能器阵列已发展了多种[4-13]，其中基于多元载荷的导波激励方法由于适用范围广，换能器设计简单而引起了学者的广泛关注。Ditri等利用简正模态展开法(Normal Mode Expansion, NME)对任意边界加载条件下导波沿空心圆管的位移分布进行了研究，给出了圆管中导波激励问题的物理解释，并基于NME方法分析了多元载荷条件下纵向模态导波激励所需的载荷条件。Tang等基于本征函数法对管道中纵向模态导波的激励问题进行了深入分析，模拟和讨论了载荷参数对单一L(0,2)模态导波激励的影响。Alleyne等发展了一种基于长度伸缩型压电元件的干耦合换能器阵列，换能器通过专用卡具安装于管道外壁并通过卡具上的预紧力调节装置使换能器与管道紧密接触，换能器阵列对管道表面施加轴对称的轴向载荷可在管道中激励纵向模态导波L(0,2)，将各换能器旋转90°可使换能器阵列对管道施加轴对称切变载荷进而在管道中激励扭转模态导波T(0,1)[14]。然而，上述多元载荷条件下轴对称模态导波激励研究均是基于理想载荷。在实际管道检测过程中，换能器阵列安装误差等因素的存在往往使各换能器对管道施加的载荷不一致而形成非轴对称载荷，进而影响期望模态导波的激发效率。

对非轴对称多元载荷条件下管道中纵向模态导波的激励问题深入研究。针对长度伸缩型换能器安装误差造成的载荷方向不一致和换能器所受预紧力不一致两种典型情况产生的非轴对称载荷，采用简正模态展开技术探讨了其对单一纵向模态导波激励的影响，并采用有限元数值模拟进行了验证。考虑实际管道检测中的非轴对称载荷，提出了一种载荷补偿策略并进行了实验验证。

1现有基础

1.1圆管中的导波

无限长空心圆柱体中弹性波传播问题的通解首先由GAZIS得到[15]。考虑应力自由边界条件，由弹性动力学理论可得到空心圆管中导波传播的频散方程。对频散方程求解可知，管道中沿轴向传播的导波有三种模态，分别为纵向模态、扭转模态和弯曲模态，其中纵向和扭转模态为轴对称模态，弯曲模态为非轴对称模态。为方便起见，采用Li等[16]所述表示方法，将上述模态表示为L(M,n)和T(M,n)，M=0,1,2,3…为周向阶次，n=1,2,3…为模数，即轴对称纵向模态和轴对称扭转模态可分别表示为L(M,n)和T(M,n)，M=0；弯曲模态可表示为L(M,n)和T(M,n),M=1,2,3…。如图1所示为内径53 mm、壁厚3.5 mm的40#钢管中导波群速度频散曲线。

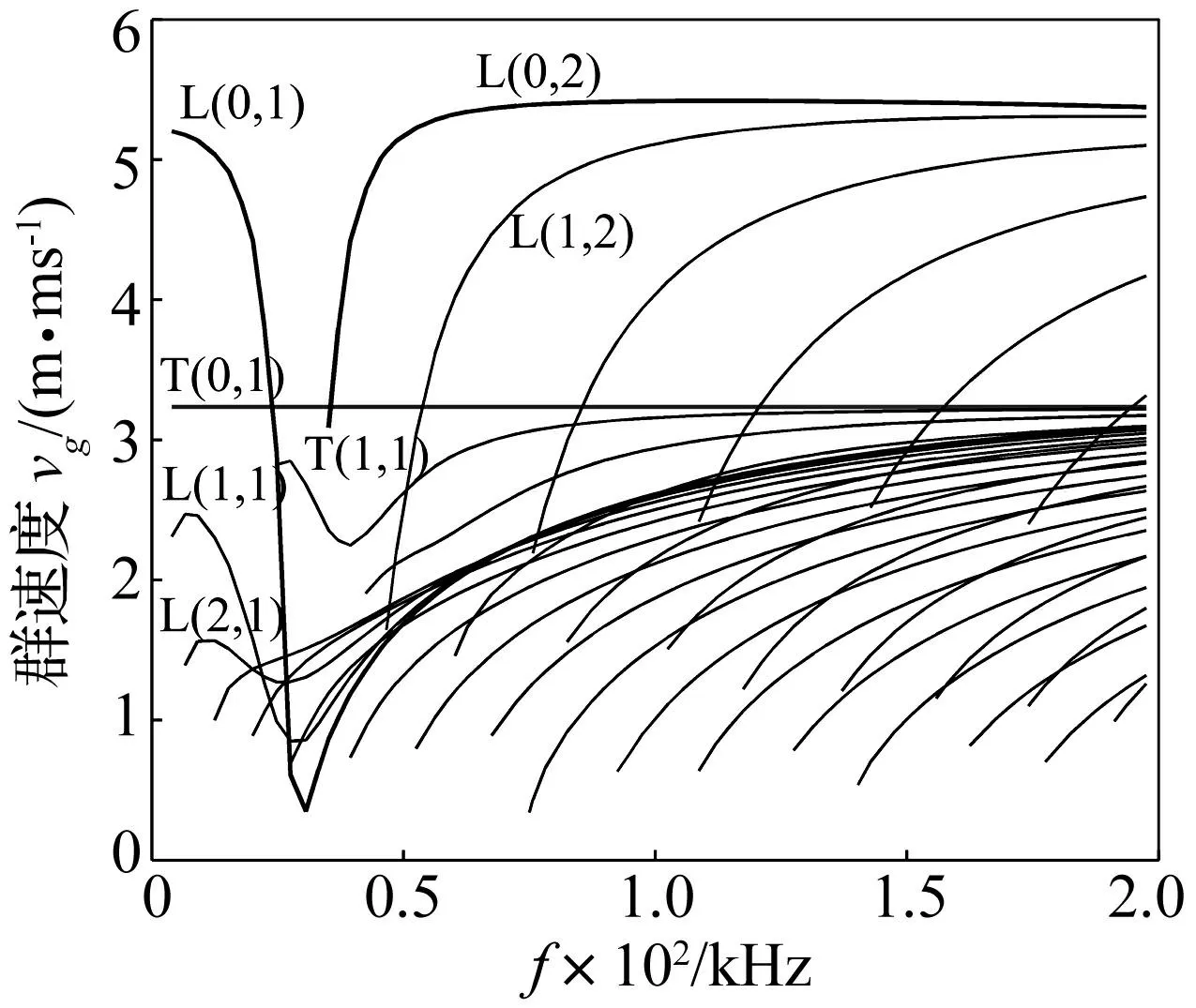
图1　内径53 mm，壁厚3.5 mm的40#钢管群速度频散曲线 Fig.1 Group velocity dispersion curves for schedule 40 steel pipe (inner diameter 53 mm, wall thickness 3.5 mm)

在导波的众多模态中，轴对称纵向模态导波L(0,2)在某频段内群速度最快且几乎为常数(见图1中的80～200 kHz频段)，这一特点使得该模态导波在所有回波信号中最先到达接收换能器，易于在时域内分辨，且波形不会发生畸变。L(0,2)模态导波的这一特点使其适于长距离管道的检测。因此，以L(0,2)模态导波激励为例，探讨非轴对称载荷对轴对称模态导波激励的影响。

1.2纵向模态导波激励

基于NME法，Ditri等建立了纵向模态导波激励幅值因子与空心圆管表面局部载荷的关系。考虑换能器在图2所示的空心圆管(内半径为a，外半径为b)外表面施加沿其径向的载荷-per，该项可表示为-p1(θ)p2(z)，其中p1(θ)为表面载荷的周向函数，p2(z)为表面载荷的轴向函数。沿圆管正向(+z)传播的导波简正模态展开幅度可表示为[4]：

(1)

式中：

(2)

(3)

图2　I个换能器沿圆管周向等间距分布示意图 Fig.2 I equally sized, equally spaced element transducers

考虑在圆管外壁有I个换能器沿圆周方向等间距分布组成阵列，换能器中心位置θ=(2η-1)π/I，其中η∈{1,2,…I}。为避免换能器之间接触，分布角γ需满足0≤γ≤2π/I。

2非轴对称载荷激励

2.1问题提出

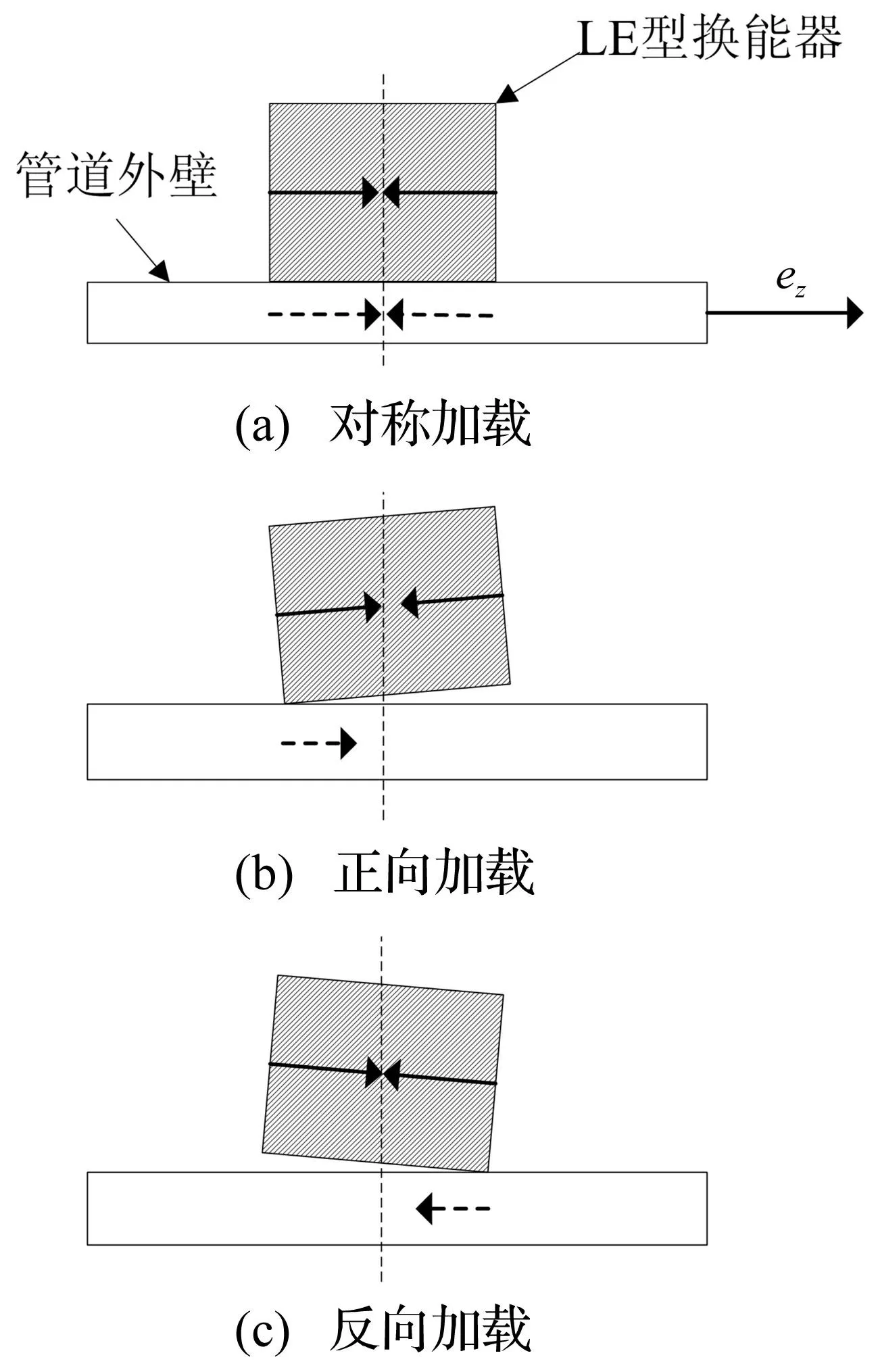
图3　LE型换能器安装及载荷施加情况示意图 Fig.3 Schematic diagram of Length-Expander transducer installation and the corresponding loading conditions

长度伸缩型压电元件(Length-Expander Elements, LE)是管道中纵向模态导波激励、接收常用的一种能量交换器件，当沿其极化方向施加交变电场时，压电元件会产生沿其长度方向的伸缩振动。对于采用LE型压电元件为敏感元件的干耦合换能器，当压电元件长度方向沿管道轴向时，换能器可对管道表面施加沿管道轴向的交变载荷。换能器与管道良好耦合时(见图3(a))，可以在管道中高效激励L(0,2)导波且可有效抑制弯曲模态导波的产生。然而，受换能器安装误差等因素的影响，换能器与管道外壁不能良好耦合。(见图3(b)和图3(c))，为两种典型的LE型换能器与管道表面耦合情况示意图。图3(b)和图3(c)所示LE型换能器施加相同的激励信号，在某一时刻LE型压电元件的振动情况如图中实线箭头所示，则两个LE型换能器在该时刻对管道施加的载荷方向是相反的，如图3中虚线箭头所示。考虑沿管道圆周布置的I个换能器，可能会出现周向分布载荷方向不一致的情况，其对纵向模态导波激励的影响是第一个问题。

为使换能器与管道能够进行良好的声波能量传递，往往需要通过卡具装置对换能器施加一定的预紧力。研究表明，换能器与管道良好接触，且卡具对各换能器施加的预紧力相同时，纵向模态导波激励可以取得良好的效果。由于各换能器所受预紧力不一致，则其对纵向模态导波激励的影响是第二个问题。

2.2载荷方向不一致影响

为简化分析，这里不考虑载荷轴向长度对导波激励的影响，即换能器对管道施加的载荷看作点载荷，轴向长度取为ΔxL。载荷数量大于激励频率处出现的最高弯曲模态数，且载荷数量是四的倍数。单个换能器对管道施加的载荷方向可以沿正向也可以沿负向，考虑I个换能器，则出现的载荷阵列就有多种情况。选取三种典型的载荷阵列进行分析：

(1) 各载荷均沿ez方向(正向)；

(2) 各载荷均沿-ez方向(负向)；

(3) 将各载荷均分到四个象限，其中第Ⅰ象限载荷沿-ez方向，第Ⅱ～第Ⅳ象限载荷沿ez方向。

“(1)” 与理想多元载荷条件下纵向模态导波的激励问题相同，载荷分布函数可看作常数，即：

p1(θ)=

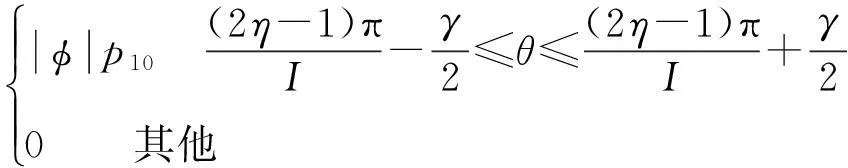
(5)

“(2)” 与理想多元载荷条件下纵向模态导波的激励问题亦相同，与“(1)”不同的是其轴向载荷分布函数为：

(6)

将式(4)和式(5)代入式(1)，可得“(1)”时的纵向导波简正模态展开幅度(M=0)：

(7)

将式(4)和式(6)代入(1)式后的结果与式(7)相比，二者仅存在正负差异。也就是说，“(1)”和“(2)”激励出的纵向模态导波幅值相同，而相位相反。

对于“(3)”，第Ⅰ象限载荷的周向分布函数p1(θ)取常数p10,轴向载荷分布函数p2(z)取常数-p20；其它象限载荷周向分布函数p1(θ)同第Ⅰ象限，轴向载荷分布函数p2(z)取常数p20。基于导波叠加原理，对于纵向模态导波激励，即M=0时，将p1(θ)和p2(z)代入式(2)和式(3)得：

(8)

将式(8)代入式(1)得到轴对称模态导波简正模态展开幅度为：

(9)

比较式(7)和式(9)可以看出，“(3)”激励出的纵向导波幅值小于“(1)”激励出的纵向导波幅值，这是由于“(3)”中不同方向的载荷激励出的纵向模态导波相位相反，经叠加后幅值变小造成的。

当M≥1时，导波激励的幅值因子计算较为复杂，为定性说明问题，这里将沿管道周向分布的多元载荷进行了简化，即将第Ⅰ象限所有载荷看作一个载荷，其在管道圆周方向的分布角为π/4，其余象限所有载荷看作一个载荷，在管道圆周方向的分布角为7π/4。

对于第Ⅰ象限载荷，其周向幅值因子和轴向幅值因子为：

(10)

(11)

对于Ⅱ～Ⅳ象限载荷，其周向幅值因子和轴向幅值因子为：

(12)

(13)

则导波激励的简正模态展开幅度为：

(14)

2.3预紧力不一致影响

由式(1)可以看出，导波激励幅值与载荷分布函数p1(θ)和p2(z)直接相关。Alleyne等实验结果表明，导波激励幅值随卡具对换能器施加的预紧力增大而增大，且呈现一种非线性关系，也就是说，预紧力与载荷分布函数之间存在着某种复杂的函数关系。虽然关于二者关系的物理描述目前尚不清楚，但仍可以认为，在其他参数相同的情况下(如换能器性能、激励信号等)，不同预紧力对应了不同的载荷分布函数。

与上述情况(3)的多元载荷简化情况相同，对于第Ⅰ象限载荷，其周向幅值因子同式(10)，轴向幅值因子为式(11)的负数，第Ⅱ～第Ⅳ象限载荷周向和轴向幅值因子分别为：

(15)

(16)

载荷阵列激励的纵向导波简正模态展开幅度为(M=0时)：

(17)

载荷阵列激励的非轴对称导波简正模态展开幅度为(M≥1时)：

(18)

由式(17)和式(18)可以看出，预紧力不一致时，载荷阵列在激励出纵向模态导波的同时也激励出了非轴对称模态导波。

2.4数值分析

数值分析方法在研究空心圆管中导波的激励以及导波与圆管特征结构相互作用方面应用广泛[17-20]。采用商用有限元软件ANSYS建立管道模型并进行仿真计算。管道参数：长1.2 m，内径53 mm，壁厚3.5 mm，40#钢。激励信号采用经Hanning窗调制的3周期正弦信号，频率80 kHz。单元模型选用壳单元shell63，沿管道圆周方向共均匀布置32个节点，并通过对节点施加激励位移来模拟载荷施加。图4为建立后的纵向模态导波激励接收有限元模型，激励节点用于对管道施加纵向激励位移，监测节点用于接收反射回波。

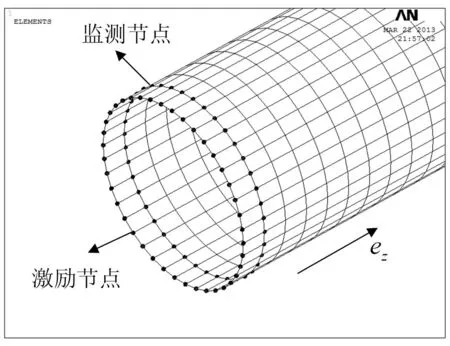
图4　管道模型网格划分及激励位移施加 Fig.4 FEM model of pipe and incentive displacement applied

由图1频散曲线可以看出，在80 kHz频率处存在另外一种纵向模态导波L(0,1)，该模态导波具有管道内外表面径向位移相对较大的特点。由于壳单元不能模拟壁厚方向上位移差别较大模态的特性，因此，L(0,1)导波实际上并没有被模拟出来[20]。分别提取32个监测节点数据，将各节点数据相加可提取纵向导波L(0,2)。以第一个节点为参考，各节点数据相对第一节点相移Mφ/2π后再相加可提取弯曲模态导波，其中M为导波周向阶次，φ为各节点与第一节点的角距离。

对应上述“(1)”、“(2)”，分别对32个激励节点同时施加沿ez方向和-ez方向的激励位移；对应“(3)”，对32个激励节点同时施加纵向位移，其中1～8节点激励位移沿-ez方向，9～32节点沿ez方向。三种加载方式对各节点施加的激励位移幅值相同，激励结果见图5和图6，各导波激励结果以“(1)”结果为参考进行了归一化处理。

如图5(a)和5(b)所示，分别为激励信号正向加载和反向加载时的导波激励结果，从图中可以看出，两种加载方式均激励出了单一的L(0,2)模态导波，且完全抑制了弯曲模态导波的产生。图5(c)为两种加载方式下的管端回波信号比较，为更清晰的反映回波信号的相位情况，将反向加载产生的管端回波幅值降低了1/2。从图5(c)可知，两种加载方式激励出的导波相位恰好相反。

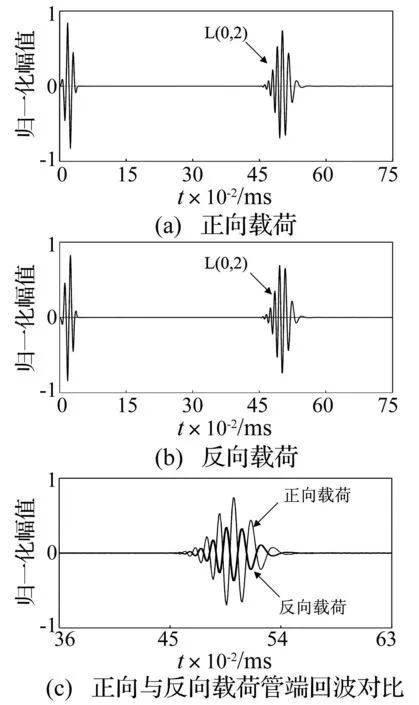
图5　同向载荷导波激励结果 Fig.5 Guided wave excitation results by applied loadings in the same direction

图6为圆管32个节点同时存在正向和反向位移加载时的激励结果。图6(a)为各监测节点数据相加提取的L(0,2)模态导波，可以看出，其幅值小于图5(a)和图5(b)所示L(0,2)幅值，这与理论预测结果相同。另一方面，此种加载方式产生了较强的弯曲模态导波，如图6(b)所示，为各监测节点数据相对第一节点相移φ/2π后相加提取的一阶弯曲模态导波。由图1频散曲线可以看出，在激励频率80 kHz附近存在多个一阶弯曲模态导波，而图6(b)显示的一阶弯曲模态导波可能是几个不同模数的一阶弯曲模态导波叠加的结果，因此其模数尚不能确定。如图6(c)所示，为管端回波L(0,2)和一阶弯曲模态导波在同一时间域上的到达时间对比，可以看出一阶弯曲模态导波到达时间相对L(0,2)导波有较为明显滞后。这是因为在80 kHz附近L(0,2)导波群速度最快(如图1频散曲线所示)，其会先于一阶弯曲模态导波到达监测节点。

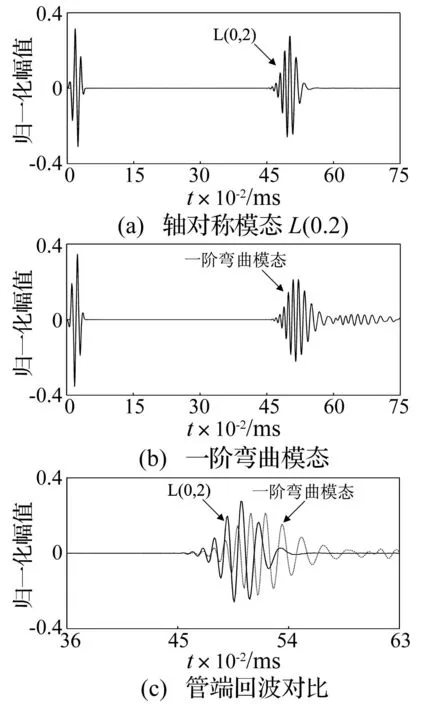
图6　载荷方向不一致导波激励结果 Fig.6 Guided wave excitation results by applied loadings in different directions

由于预紧力与载荷分布函数的量化关系未知，因此，此处的数值模拟仅是一种定性分析，即通过改变对各节点施加的激励位移幅值来模拟预紧力不同。将沿圆管周向布置的32个节点均分为4个象限，其中第Ⅰ象限施加的激励位移幅值是其他象限的1/2，激励结果见图7。图7(a)为提取的L(0,2)模态导波，其幅值小于图5(a)和图5(b)所示L(0,2)幅值。图7(b)为提取的一阶弯曲模态导波，可见，由于换能器所受预紧力不一致而造成的各载荷大小不一致，同样会产生弯曲模态导波。另外，一阶弯曲模态导波到达监测节点时间相对L(0,2)导波仍然有滞后，限于篇幅关系，在此不再进行对比分析。

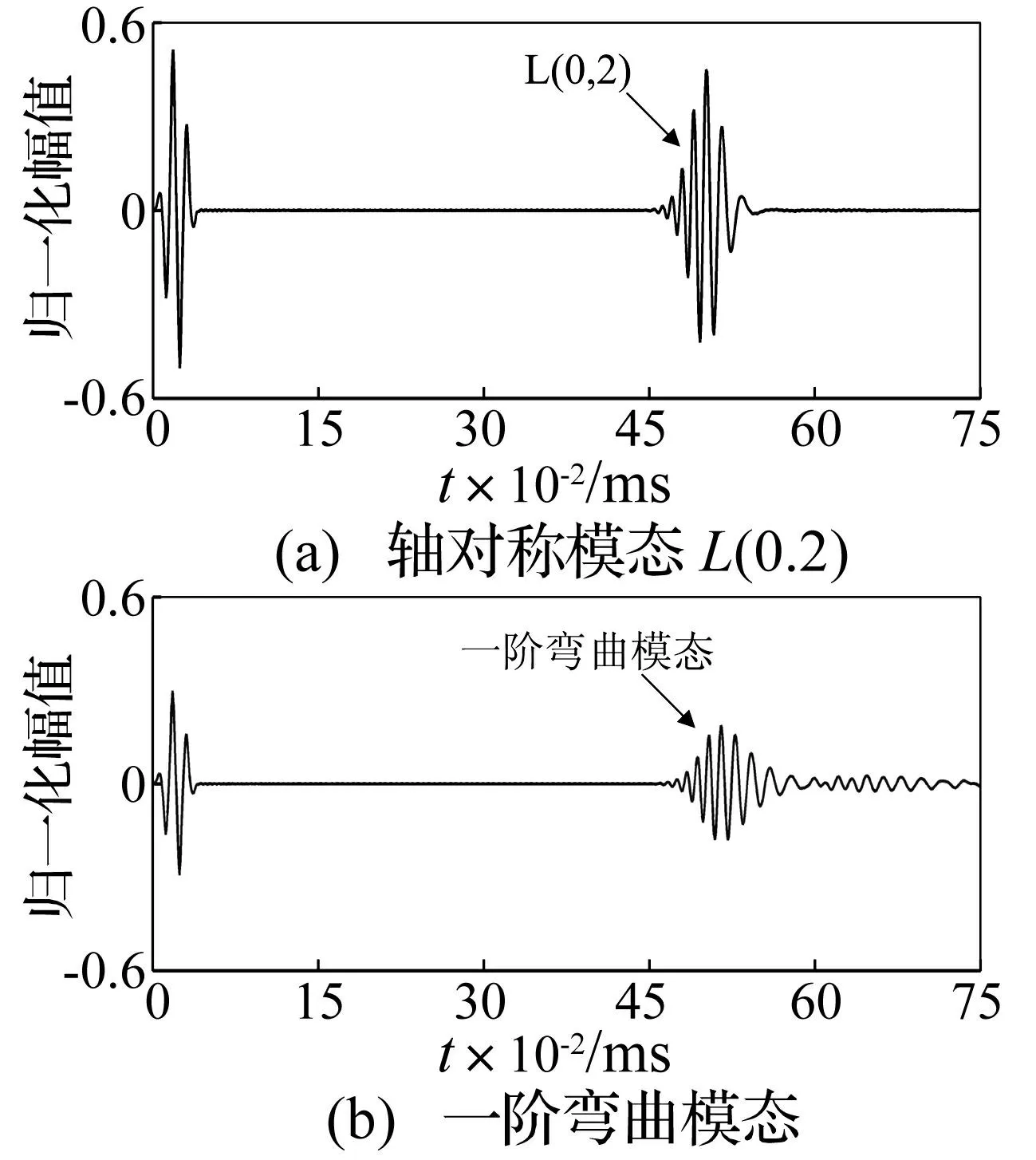
图7　各节点施加激励位移幅值不一致导波激励结果 Fig.7 Guided wave excitation results by applied inconsistent amplitude loadings

2.5补偿策略

由上述分析可知，对于沿管道周向分布的多元激励载荷，当载荷方向或载荷大小不一致时，均会激励出较多的弯曲模态导波。考虑实际管道检测需要，希望消除或降低二者对单一模态导波激励的影响。对于沿管道周向布置的LE型换能器阵列，由于其安装误差的存在，较易出现载荷方向不一致的现象。对于剪切型压电元件，由其振动特性可知，应变发生表面在某一时刻产生的应变沿同一方向。因此，沿管道周向布置的基于剪切型压电元件的换能器阵列能够在同一时刻对管道表面施加同方向的载荷，这有利于单一模态导波的激励。一般而言，激励导波幅度与换能器输出能量相关，而该输出能量又与载荷分布函数相关。因此，换能器激励信号及卡具对换能器施加的预紧力是影响载荷分布函数(或者说导波激励幅度)的两个重要参数。针对导波激励过程中出现的非轴对称载荷，调节上述两个参数，可使各载荷大小尽量一致，进而有效降低非轴对称载荷对单一模态导波激励的影响。

3实验研究

实验研究的目的主要是验证上述载荷补偿方法。干耦合换能器敏感元件采用厚度剪切型压电陶瓷晶片，晶片尺寸长l=12 mm，宽w=3 mm，厚t=0.5 mm。卡具装置采用模块化设计，每个模块含有独立的预紧力调节螺丝及弹簧，模块之间通过销轴连接成链式换能器阵列，位于阵列端部的两模块含有锁紧装置，能使阵列首尾相连并锁紧于管道外壁，旋紧各模块上的调节螺丝使弹簧对换能器施加一定的预紧力进而完成换能器阵列在管道上的安装。

导波激励实验在长2.6 m，壁厚6.5 mm，外径102 mm的40#钢管中进行。实验系统原理图见图8所示，管道端部外壁共均匀布置16个干耦合换能器并沿逆时针方向分别编号1～16，这些换能器被均分到8个象限中，每个象限中的两个换能器彼此并联且对应一个独立的导波激励接收通道。通过旋紧预紧力调节螺丝，使分别位于第4、第5、第6、第7象限的8、10、11和14号换能器所受预紧力约为其他换能器所受预紧力的一半。激励信号采用经Hanning窗调制的5周期正弦信号，频率为80 kHz。各象限激励信号由PC控制任意波形发生单元并行产生，并分别经功率放大单元线性放大后加载至对应象限换能器。各象限换能器接收到的回波信号由高速数据采集单元进行并行采集后送入PC处理和显示。

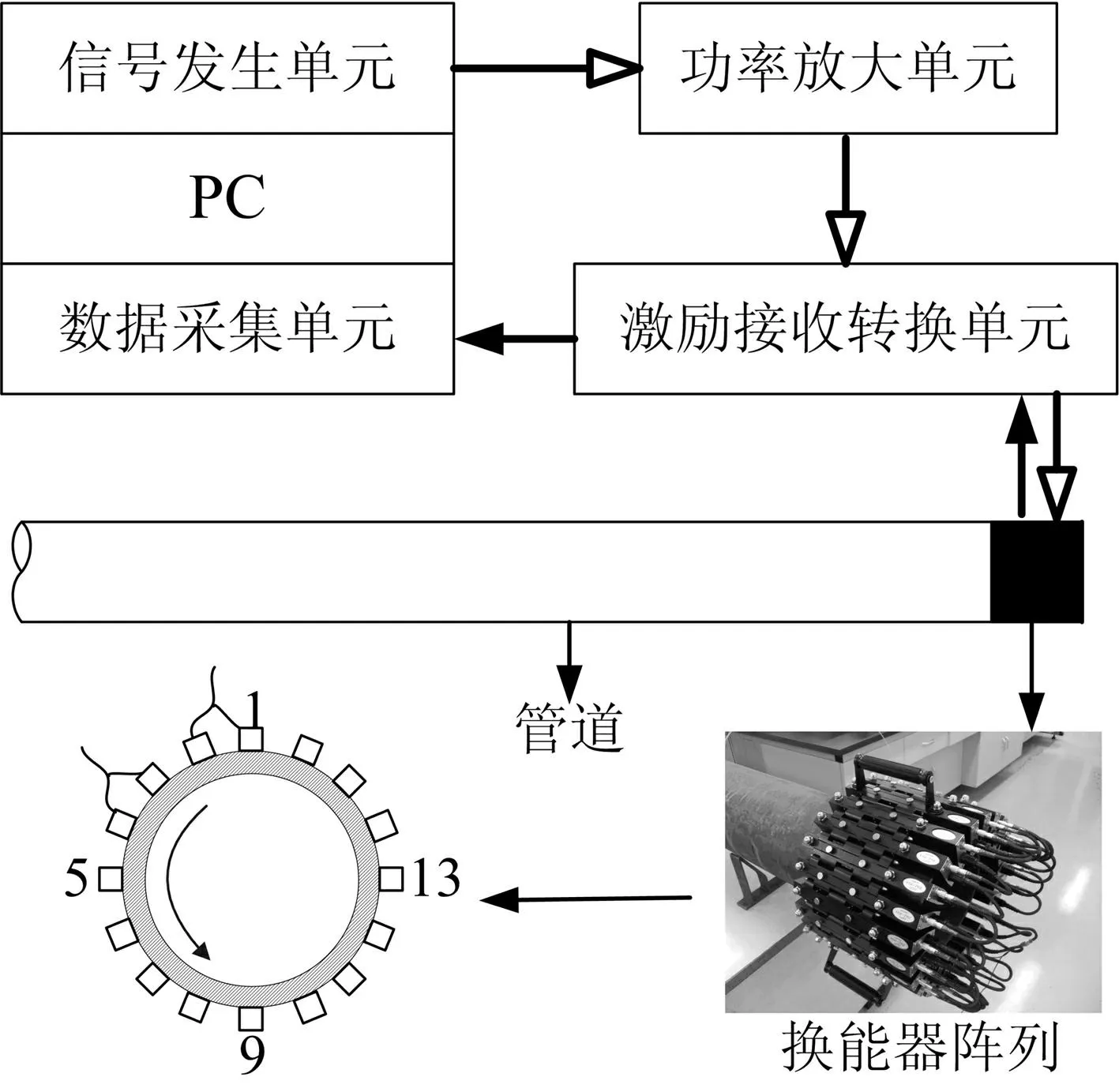
图8　实验系统原理图 Fig.8 Schematic diagram of equipment

如图9所示为各换能器首次被同时激励时接收到的回波信号，其中图9(a)为提取的L(0,2)模态导波，图9(b)为提取的一阶弯曲模态导波。从图9(b)可知，换能器阵列激励出了较多的弯曲模态导波，同时图9(a)中的噪声信号偏高，这些都是由于部分换能器与管道耦合状况不好造成的。

由于在实际管道检测过程中事先并不清楚换能器与管道的耦合状况，同时也不清楚管道中是否存在缺陷，因此需要进行载荷补偿的第一步来判断各象限换能器与管道的耦合状况。如图10所示为完成载荷补偿第一步后得到的8个L(0,2)模态导波幅值图。从图10中可以清晰的看出，位于第4、第5、第6、第7象限的换能器与管道耦合状况不佳，这与实验初期设定是吻合的。

图9　补偿前导波激励结果 Fig.9 Guided wave excitation results before compensation

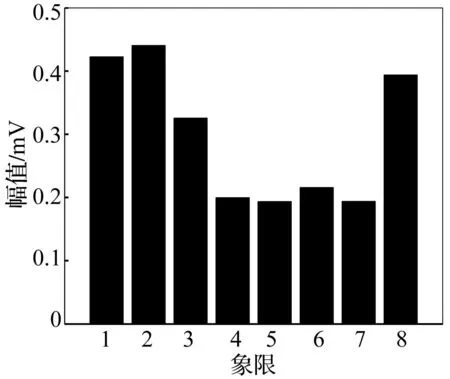
图10　补偿前各象限L(0,2)导波幅值 Fig.10 The amplitude of L(0,2) mode in each quadrant before compensation

图11　补偿后的导波激励结果 Fig.11 Guided wave excitation results after compensation

以图10中各象限L(0,2)模态导波幅值重新作为多元载荷激励条件进行空间傅里叶变换，得到该载荷条件下的一阶弯曲模态导波幅度和轴对称模态导波幅度之比为-17 dB，因此需要对初始激励载荷进行补偿。选取图10中第5象限换能器幅值为参考幅值，并与各象限L(0,2)模态导波幅值相比得到载荷补偿系数。利用该载荷补偿系数进行载荷补偿方法的第四步，换能器阵列接收到的回波信号如图11所示，其中图11(a)为提取的L(0,2)模态导波，图11(b)为提取的一阶弯曲模态导波。相比图9(b)中的一阶弯曲模态导波，图11(b)中的一阶弯曲模态导波幅度明显减小。同时，相比图9(a)中的噪声水平，图11(a)中的噪声水平也有了较大改善。结果表明，载荷补偿方法对于非轴对称载荷起到了较好的补偿作用。

4结论与讨论

针对两种典型的非轴对称载荷，采用简正模态展开技术及数值方法详细论述了其对管道中纵向模态导波激励的影响。在此基础上，针对实际管道检测中出现的非轴对称载荷需要，提出了一种载荷补偿策略并进行了实验验证。总结全文，得到如下结论：

(1) 对于沿管道周向分布的多元载荷阵列，如果其在同一时刻对管道施加同方向的载荷且载荷大小一致，则可在管道中高效激励纵向模态导波；如果载荷阵列在同一时刻对管道施加的载荷方向不一致，则激励出的纵向模态导波幅值相比同向载荷阵列会变小，并将激励出弯曲模态导波。这主要是由于不同方向载荷产生的导波相位相反，对于周向分布的载荷阵列，依据导波叠加原理，各载荷激励出的纵向模态导波叠加后幅值变小，弯曲模态导波不会完全抵消造成的。

(2) 卡具对各换能器施加的预紧力是影响纵向模态导波激励的另一重要参数，如果各换能器所受预紧力不一致，则将影响纵向模态导波的激发效率，同时也会激励出弯曲模态导波。

(3) 针对实际管道检测过程中出现的非轴对称载荷，论文提出的载荷补偿策略通过动态调整激励信号幅度能够有效抑制弯曲模态导波的产生，同时也有助于改善导波信号的噪声水平。

(4) 随着导波技术的发展，纵向弯曲模态导波也用于了管道损伤检测，纵向弯曲模态导波激励在理想载荷条件下需要动态调整各象限换能器的激励信号幅度与延时时间，在实际管道检测过程中，在保证各象限换能器激励信号幅度变化的同时再对载荷进行补偿将变得更加复杂，对于该问题我们将持续关注。

参 考 文 献

[1] Lowe M J S, Alleyne D N, Cawley P. Defect detection in pipes using guided waves[J]. Ultrasonics, 1998, 36(1):147-154.

[2] Rose J L. A baseline and vision of ultrasonic guided wave inspection potential[J]. Journal of Pressure Vessel Technology, 2002,124(3):273-282.

[3] 何存富，吴斌，范晋伟. 超声柱面导波技术及其应用研究进展[J]. 力学进展，2001; 31(2): 203-214.

HE Cun-fu, WU Bin, FAN Jin-wei. Advances in ultrasonic cylindrical guided waves techniques and their applications[J]. Advances in Mechanics, 2001, 31(2):203-214.

[4] Ditri J J, Rose J L. Excitation of guided elastic wave modes in hollow cylinders by applied surface tractions [J]. Journal of Applied Physics, 1992,72(7):2589-2597.

[5] Tang Li-guo, Cheng Jian-chun, Xu Xiao-mei. Mechanism of the excitation of single pure modeL(0,2) and its interaction with the defect in a hollow cylinder [J]. Chinese Physics, 2007, 16(4): 1062-1071.

[6] Alleyne D N, Cawley P. The excitation of lamb waves in pipes using dry-coupled piezoelectric transducers [J]. Journal of Nondestructive Evaluation, 1996,15(1):11-20.

[7] Quarry M, Rose J L. Multimode guided wave inspection of piping using comb transducers [J]. Materials Evaluation, 1999,57(10):1089-1090.

[8] Shin H J, Rose J L. Guided waves by axisymmetric and non-axisymmetric surface loading on hollow cylinders [J]. Ultrasonics, 1999,37(5):355-363.

[9] Liu L, Avioli M J, Rose J L. Incident angle selection for the guided wave inspection of pipe defect [J]. Insight, 2001,43(2):89-92.

[10] Zongqi Sun, Li Zhang, Rose J L. Flexural torisonal guided wave mechanics and focusing in pipe [J]. Journal of Pressure Vessel Technology, 2005,127(4): 471-478.

[11] Li J, Rose J L. Angular-profile tuning of guided waves in hollow cylinders using a circumferential phased array [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2002,49(12):1720-1729.

[12] Hay T R,Rose J L. Flexible piezopolymer ultrasonic guided wave arrays [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2006, 53(6):1212-1217.

[13] Kim G, Moon Y, Park H S K, et al. Generation and detection torsional guided waves using magnetostrictive sensors of crossed coils [J]. NDT&E International, 2011, 44(2): 145-151.

[14] Alleyne D N, Pavlakovic B, Lowe M J S, et al. Rapid long range inspection of chemical plant pipework using guided waves [J]. Insight, 2001,43(2):93-96.

[15] Gazis D C. Three-dimensional investigation of the propagation of waves in hollow circular cylinders. I. Analytical foundation [J]. Journal of the Acoustical Society of America, 1959,31(5):568-573.

[16] Li J, Rose J L. Angular-profile tuning of guided waves in hollow cylinders using a circumferential phased array [J]. IEEE Transcations on Ultrasonics, Ferroelectrics, and Frequency Control, 2002,49(12): 1720-1729.

[17] Lowe M J S, Alleyne D N, Cawley P. The mode conversion of guided wave by a part-circumferential notch in a pipe [J]. Journal of Applied Mechanics, 1998, 65(3):649-656.

[18] Cawley P, Lowe M J S, Simonetti F, et al. The variation of the reflection coefficient of extensional guided waves in pipes from defects as a function of defect depth, axial extent, circumferential extent and frequency [J]. Proceeding of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2002,216(11):1131-1143.

[19] Demma A, Cawley P, Lowe M, et al. The reflection of the fundamental torsional mode from cracks and notches in pipes [J]. Journal of the Acoustical Society of America, 2003,114(2): 611-625.

[20] Wang Xiao-jun , Peter W T, Chris K M, et al. Experimental investigation of reflection in guided wave-based inspection for the characterization of pipeline defects [J]. NDT&E International, 2010,43(4):365-374.