与r的一次方成正比有心力作用下质点的运动研究

与r的一次方成正比有心力作用下质点的运动研究

李 阳王 宏韩艳玲

[中国地质大学(武汉)数学与物理学院湖北 武汉430074]

中国地质大学(武汉)2014-2015学年度教学实验室开放基金项目资助，项目编号：SKJ2014216

摘 要：在水平面上受稳定约束的弹簧振子运动模型，实质上是一个与距离r的一次方成正比有心力作用下质点的运动问题.本文利用拉格朗日方程建立了该运动模型在极坐标系中的动力学方程，分别采用泰勒级数展开的方法和Matlab数值模拟的方法对该模型的动力学方程进行了计算，作出了相应的坐标随时间的演化曲线、运动相图、运动轨迹，并将两种方法得出的结果进行了比较，研究发现,当初速度较小时，弹簧振子在径向的运动是周期性的简谐运动，在横向的运动是非线性增大的，在平面上的运动是准周期的.

关键词：水平面稳定约束弹簧振子极坐标系泰勒级数展开Matlab数值模拟

收稿日期：(2015-06-01)

作者简介：李阳(1991-)，男，在读硕士研究生,主要从事物理教学论研究.

通讯作者：韩艳玲(1965- )，女，博士，教授，硕士生导师，主要从事大学物理教学和光子晶体理论研究.

受稳定约束的弹簧振子是由一个大密度的实心小球和一个轻质弹簧构成的，弹簧的一端固定不动，另一端和小球相连，它既是力学中不可积系统的典型模型[1]，同时，又是工程学中典型的非线性运动之一.

在理论力学中，人们研究较多的是竖直平面内的弹簧摆运动[1～4]，对于水平面上受稳定约束的弹簧振子运动研究的较少，实际上，它是一个与距离r的一次方成正比有心力作用下质点的运动问题.

截止目前，人们已经研究了与距离r的二次方成反比、三次方成反比、五次方成反比有心力作用下质点的运动[5～7]，但是，与距离r的一次方成正比有心力作用下质点的运动研究却鲜见报道. 鉴于此，本文对该模型下的这一问题进行了研究与分析，写出来与读者进行交流.

1系统的动力学方程

如图1所示，在水平面上受稳定约束的弹簧振子是由一个轻质弹簧和一个大密度的实心小球构成的，其中弹簧的劲度系数为κ，原长为l0，小球的质量为m，直径忽略不计，视为质点.

图1　水平面上受稳定约束的弹簧振子

在水平面上，忽略阻力影响，某一时刻对小球施加一个瞬时的冲量，小球开始运动，弹簧对小球的弹力即为小球所受的合力，且力的方向所在的直线始终通过极点O,整个系统为有心的保守力系，其拉格朗日方程为

(1)

系统的动能和势能分别为

系统的拉格朗日函数为

(2)

将式(2)代入式(1)，其中q1=r，q2=θ，可得

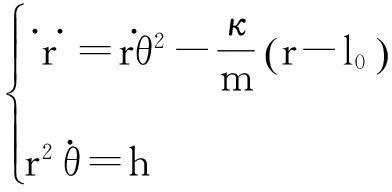
(3)

其中h为常量.

将式(3)中的第二式代入第一式，并对第二式进行处理可得系统的动力学方程为

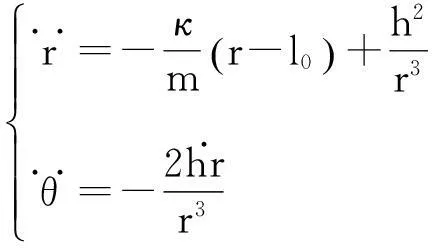
(4)

2近似的解析解

式(4)第一式是一个二阶的非线性微分方程，若直接求其通解，则无法求出，但通过近似处理，可以得到相应的解析解.

令x=r-l0，则式(4)可以改写为

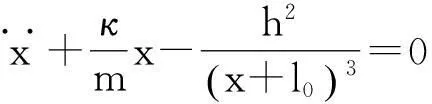
(5)

(6)

将式(6)代入式(5)，整理可得

(7)

令

则式(7)可化为

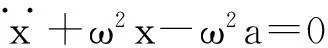
(8)

式(8)的解析解为

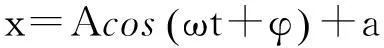
其中A和φ均为参数，对于微振动，x是一个随时间变化的量，所以A≠0，即

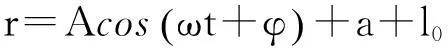
(9)

3数值模拟

为了使该研究更具普遍性，在该体系中，随机选取参数m=0.02kg，κ=0.5N/m，l0=1.0m，令积分常数h=1. 采用Matlab软件对系统的动力学方程、运动轨迹以及近似解分别进行数值模拟.

3.1动力学方程的数值解

对于式(4)，采用四阶的Runge-Kutta方法进行数值计算.为了便于比较，选定两组初始条件进行数值模拟.

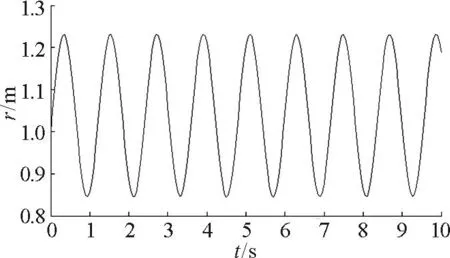
图2　初速度v 0=1.414 m/ s时的r-t曲线

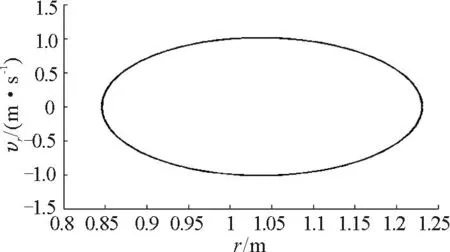
图3　初速度v 0=1.414 m/ s时的 相图

图4　初速度v 0=1.414 m/ s时的θ-t曲线

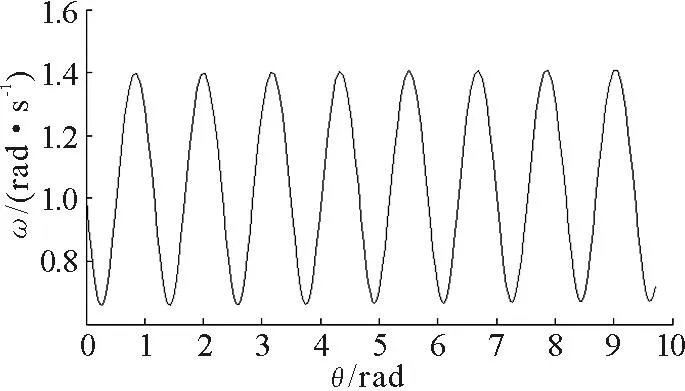
图5　初速度v 0=1.414 m/ s时的 相图

图6　初速度v 0=1.414 m/ s时r随θ变化的曲线

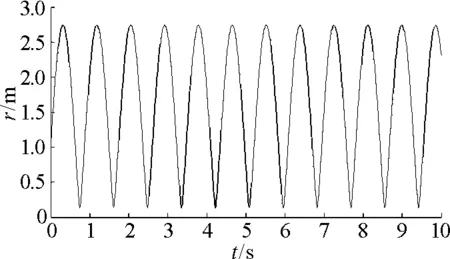
图7　初速度v 0=10 m/ s时的r-t曲线

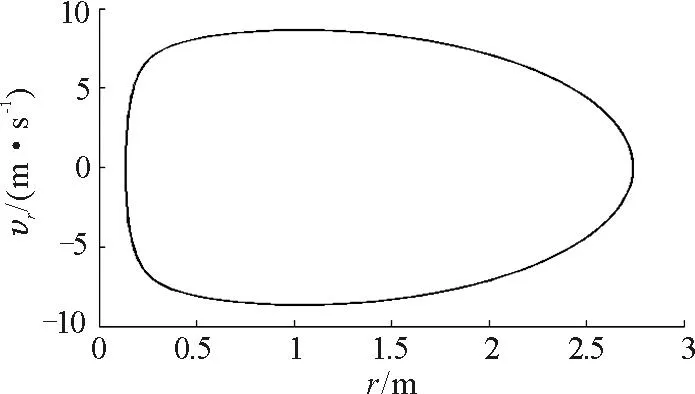
图8　初速度v 0=10 m/ s时的 相图

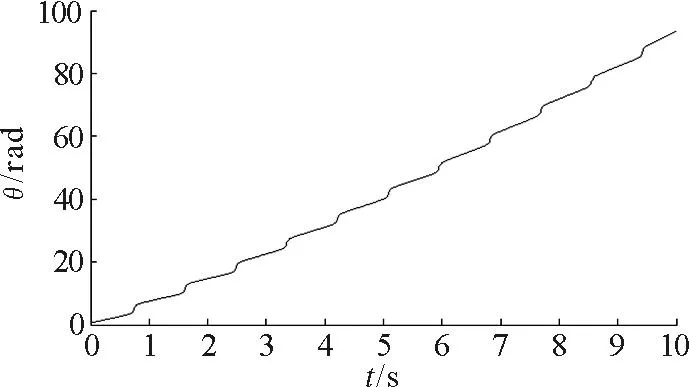
图9　初速度v 0=10 m/ s时的θ-t曲线

图10　初速度v 0=10 m/ s时的 相图

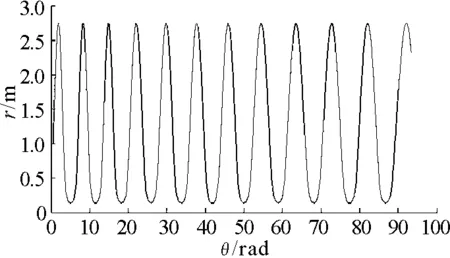
图11　初速度v 0=10 m/ s时r随θ变化的曲线

3.2不同初始条件下振子的运动轨迹

为了更好地研究弹簧振子在水平面上的运动情况，分别模拟出振子在两组初始条件下的运动轨迹.在第一组初始条件下，取计算时间为50s，和前面相对应，步长取0.05s，则振子的运动轨迹如图12所示；在第二组初始条件下，取计算时间为50s，步长对应取0.01s，则振子的运动轨迹如图13所示.

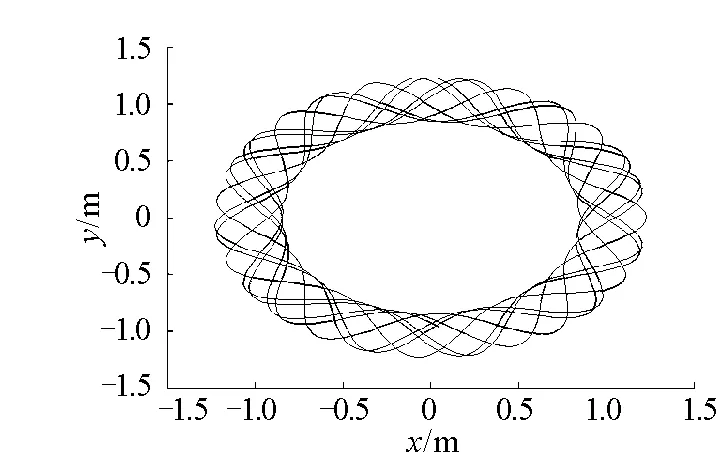
图12　初速度v 0=1.414 m/ s时振子的运动轨迹

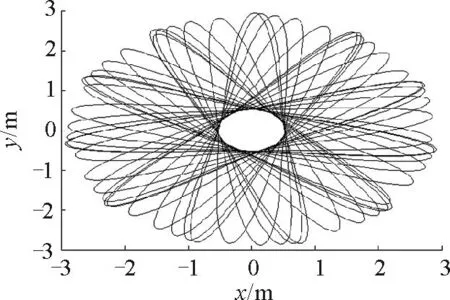
图13　初速度v 0=10 m/ s时振子的运动轨迹

3.3近似解析解与数值解的拟合

当初速度为v0=1.414m/s时，对于已选定的体系可计算出相应参数

ω=5.291 5rad/sa=0.035 7m

模拟时取计算时间为10s，步长为0.05s， 令初相φ=1.754 9rad，A=0.195m，则式(4)经处理后的近似解析解与直接数值解的拟合如图14所示.

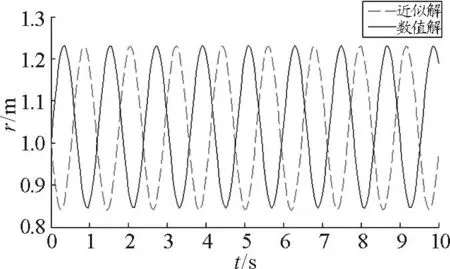
图14　当v 0=1.414 m/ s时径向两种解的拟合

4对结果的讨论

以上我们对系统的动力学方程分别采用了两种不同的方法进行了计算.

一种是在微振动的情况下，对非线性方程进行了泰勒级数展开，保留了一阶小量，得到了沿径向的质点运动学方程，从中可以看出质点在径向做的是简谐振动，且简谐振动的频率取决于系统的属性.

另一种是在Matlab软件中利用四阶的Runge-Kutta方法直接对非线性方程求数值解.当质点的初速度较小时，从图2和图3可以看出，质点在径向做的是周期性运动.如图14所示，通过选取合适参数，将径向的数值解与径向的近似解析解进行拟合，也可以看出当初速度较小时，质点在径向做的是周期性的简谐振动.

当质点的初速度较小时，从图4和图5可以看出，在横向，角度随时间呈非线性增大，角速度随时间的变化带有明显的周期性. 从图6可以看出，随着横向角度的增大，质点在径向的运动具有周期性. 从图12振子在水平面上的运动轨迹可知，振子在水平面上的运动是准周期的.

当质点的初速度较大时，从图7和图8可以看出，质点在径向的运动出现了一种有趣的现象，即当弹簧振子处于伸长状态时，质点在径向的运动是周期性的，当弹簧振子处于压缩状态时，质点会很快被弹出并开始下一次的运动，这可能是因为弹簧的压缩量已经达到了所能承受的极限所致. 且在径向运动的振幅要比初速度较小时大很多.

当质点的初速度较大时，从图13振子在水平面上的运动轨迹可知，振子在水平面上的运动是准周期的，且振幅比初速度较小时大很多. 从图9和图10可以看出，在横向，角度随时间依然呈非线性增大，但角速度随时间的变化已经没有了周期性，横向的相图十分复杂. 从图11可以看出，随着横向角度的增大，质点在径向的运动只在弹簧振子处于伸长状态时具有周期性，这与前面的分析是一致的.

5结语

在水平面上受稳定约束的弹簧振子运动模型，实质上是一个与距离r的一次方成正比有心力作用下质点的运动问题.

本文利用拉格朗日方程建立了该运动模型在极坐标系中的动力学方程，分别采用泰勒级数展开的方法和Matlab数值模拟的方法对该模型的动力学方程进行了计算，作出了相应的坐标随时间的演化曲线、运动相图、运动轨迹，并将两种方法得出的结果进行了比较.研究发现,当初速度较小时，弹簧振子在径向的运动是周期性的简谐运动，在横向的运动是非线性增大的，在水平面上的运动是准周期的.

致谢：本文在撰写的过程中曾与湖北文理学院物理系夏清华教授、杨正波副教授、高翔老师进行过有益讨论，在此表示感谢.

参 考 文 献

1李云龙，倪致祥. 弹簧摆振动能变化的数值研究.阜阳师范学院学报，2009，26(4)：45～48

2杨正波，夏清华，刘思平. 不同控制参数下的弹簧摆. 大学物理，2011，30(5)：23～27

3管慧，李维善. 弹簧摆运动的研究. 大学物理，2010，29(3)：16～20

4司丽荣，张竞夫.弹簧摆内共振现象的实验研究.物理实验，2002，22(3)：13～16

5龚峻明.有心力与平方反比轨道.沈阳农业大学学报，1987,18：25～30

6李秀芬. 距离三次方反比有心力作用下质点的运动. 科技资讯，2009，9(3)：239

7那仁满都拉. 五次方反比引力作用下质点运动的轨道. 大学物理，2012，31(11)：9～10