初中数学数形结合解题思想的应用

吕淑华

在初中数学学习中涉及很多数学思想的学习，其中数形结合是一种比较实用和常见的，正确的把握数与形之间的对应关系，从而实现数与形之间的转化，帮助学生轻松解决数学问题。数形结合思想的运用能够将无形的内容转化成为有形的，让学生形成一个形象的思维，对问题进行更加透彻的分析，更加直观形象地帮助学生进行数学分析，能够有效地帮助学生提高逻辑思维能力和观察能力。数形结合思想在整个初中数学学习中有着重要的应用价值，合理的运用，能够帮助学生提高对数学的学习积极性和兴趣。

一、有理数中的数形结合思想

有理数的学习是初中数学学习阶段一个比较基础的内容，如果单纯地讲解有理数的概念知识，学生很难对其形成清晰的理解，总体来说学习起来是比较抽象的，不能形成清晰形象的概念认知。为了让学生能够更好地理解这一数学教学内容，引入数形结合的思想，同时这也是有理数体现数形结合思想的典型代表，数轴的应用能够让学生对有理数形成更加具体的概念，每一个有理数在数轴上都有一个唯一的点与之对应，引入这种数形结合的学习方式之后，其他有关有理数的问题就可以更加顺利地开展了。与之相关的内容还有有理数大小的比较，主要就是通过有理数在数轴上的位置关系决定的，固定越是靠在数轴右侧的有理数越大，以0为分界点，分为正有理数和负有理数，还有就是有理数绝对值、相反数的学习，都可以通过数轴的形式轻松地学习，绝对值的比较可以通过两个有理数与0之间的距离大小来比较，距离越远的绝对值越大，相反数在数轴上就更加容易了，只需要以0所在的位置为对称轴，找到数轴上相应的点就可以了。数形结合思想的引入，让学生在学习有理数的过程中更加轻松简单，对于一些概念定义的介绍，借助数形结合的思想也更加容易完成，能够有效提高教学效率，激发学生的学习兴趣。

二、概率中的数形结合思想

概率也是初中数学中涉及的一个重要内容，主要就是对一件事情发生的概率进行分析，分析发生的次数占总次数的百分比，从而得出一定的概率数据，这也是初中数学考题中常涉及的一类题目，是考查学生逻辑思维能力以及判断能力的一个知识点，需要有严密的逻辑思维。做到不重不漏，这样才能够得到正确的答案。概率问题其实并不难，只要分析思路清晰，将所有的情况罗列出来再进行分析判断就能够轻松解决问题，一些学生觉得概率比较难学，主要就是觉得涉及的情况太过复杂，同时又容易出现思想漏洞，导致做题的时候容易出现错误。其实正确运用数形结合的思想就能够帮助学生解决这一问题，一般来说树状图是比较常见的一种形式，通过分支来表示各种情况，形状就像大树的分支一样，能够形象生动地呈现在学生面前，帮助学生轻松解决数学概率问题。

三、函数中的数形结合思想

函数是教学的重点同时也是难点，函数复杂多变的形式以及复杂的计算方法和性质概念都是让学生感到头疼的地方，一些学生甚至对函数学习产生畏惧心理，逐渐失去了学习的兴趣。其实函数并没有学生认为得那么复杂难懂，只是学生还没有掌握正确的解题方法而已，函数本身就是代数和几何的综合体。每种函数都有其特定的表达式和图像，在数学学习中常会让学生对函数性质进行分析，针对图形对函数表达的含义进行理解等，图形的设置就凸显了数形结合的思想，对于函数题目的研究和解决有很大的帮助，采用数形结合的思想能够起到事半功倍的效果。

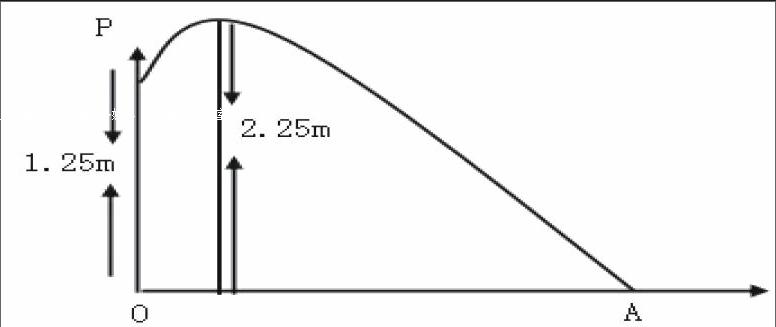
比如，某公园要建造一个圆形喷水池，在水池的中央垂直于水面的地方安装一个柱子OP，O点恰巧在水面的中心处，OP=1.25米，由柱子顶端P点喷水，水流喷向各个方向并呈现抛物线的形状，为了美观漂亮，设计成水流在距离OP为1米的地方达到最大高度2.25米，那么水池的半径至少是多少米才不至于让水喷出来？这是一个比较实际的函数应用问题，其中涉及的是抛物线的相关知识，先分析题目中给出的变量和不变量，确定各个量之间的关系，其实就是求解抛物线变量的问题。

根据画出的图形可以清楚了解到，其实这就是一个最大高度为2.25的抛物线，最终结果就是求出O点到A点的距离，也就是让水流不喷出水池的最小半径，以数形结合的方式进行分析，将题目中给出的数字变量都在图像中表述出来，做到清晰明了地将数形结合在一起，数字因为图形而变得更加直观，图形因为数字而变得更加具体，二者实现了完美结合，巧妙运用这一数学思想，让学生感觉到其实函数并不是那么难学，只需要理解题意，根据题目中给出的代数信息转化成图形信息，将二者结合在一起，就能够轻松解决数学问题，实现动静的巧妙转化，提高学生的学习能力。