细胞信号网络功能鲁棒的简并性拓扑特征

细胞信号网络功能鲁棒的简并性拓扑特征

满梦华1，张娅1，蔡娜2，马贵蕾1，原亮1，褚杰1

(1.军械工程学院电磁环境效应国家级重点实验室，石家庄 050003；

2.军械技术研究所信息化与标准室，石家庄 050003)

摘要：细胞信号网络对于外界环境的干扰表现出优良的鲁棒性，但是其维持功能鲁棒的内在机制尚未明确，本文研究了细胞信号网络功能鲁棒性的拓扑特征。选择布尔网络模型模拟细胞网络的动态行为，利用网络节点状态的扰动模拟外界环境干扰。基于演化策略探寻不同网络拓扑的功能并分析其在干扰环境下的鲁棒性，采用埃德尔曼提出的基于信息论的计算方法评估网络拓扑的简并度、冗余度和复杂度等拓扑属性，对比分析它们与功能鲁棒度的相关性及作用机理。结果显示，在网络模型的演化过程中，其拓扑简并度与功能鲁棒度显著正相关，相关性水平高于拓扑冗余度与鲁棒度的相关性。并且，随着鲁棒度的提升，网络的节点数和复杂度也随之升高，同样简并度与网络的节点数和复杂度的相关性高于拓扑冗余度与网络的节点数和复杂度的相关性。这说明增加的网络节点以简并的方式同时提高了网络拓扑的鲁棒度和复杂度。因此，细胞网络功能鲁棒性的拓扑特征是简并而不是冗余，简并为解决生物系统的复杂问题提供了有效手段，为人工系统的可靠性设计提供有益的借鉴。

关键词：细胞信号网络；布尔网络模型；简并性；冗余性；鲁棒性

中图分类号：O441.1文献标志码：A

收稿日期：2014-09-29;修回日期：2014-11-18.

基金项目：作物生物学国家重点实验室开放课题(NO.2013KF15)。

作者简介：陶璐，男，硕士研究生，研究方向：生物信息学，数据挖掘；E-mail:taolu025@163.com.

doi:10.3969/j.issn.1672-5565.2015.01.09

Degenerate topology analysis of robustness in cellular signaling network

MAN Menghua1, ZHANG Ya1, CAI Na2, MA Guilei1, YUAN Liang1, CHU Jie1

(1.NationalKeyLaboratoryonElectromagneticEnvironmentalEffects,OrdnanceEngineeringCollege,Shijiazhuang050003,China;

2.InformationandStandardOffice,OrdnanceTechnologyInstitution,Shijiazhuang050003,China)

Abstract：Cellular signaling network shows good robustness during interference, but the intrinsic mechanism about it is still not clear. This study aims to analyze the topological structure properties of the cellular signaling network. Boolean network was used to simulate the dynamic cellular signaling network, and the disturbance of network nodes was used to simulate the interference of external environment. The function of different topological networks was explored by using evolutionary strategy to analyze their robustness under various interference environments. By adopting the quantitative definitions proposed by Edelman et al, we measured the topological characteristics of degeneracy, redundancy and complexity in the evolved Boolean networks, and compared their mechanism and contributions to the robustness. As is shown in the results, in the progress of evolution of the network, the degeneracy is positivly correlatlive with the robustness significantly, and the correlation coefficient between the degeneracy and the robustness is better than that between the redundancy and the robustness. And network nodes and complexity increase with the robustness. They also have a better correlation with degeneracy than that with redundancy,which demonstrates that the increased nodes improve the robustness and complexity in a degenerate way. Therefore, the topology characteristic of cellular signaling network is the degeneracy rather than the redundancy. The degeneracy provides an efficient method for solving the complex problems of biology system and offers references for the reliability design of manual system.

Keywords：Cellular signaling network; Boolean network; Degeneracy; Redundancy; Robustness

细胞信号转导是指细胞通过细胞膜或细胞内的受体感受外界刺激或信号，并将细胞外信号进行转换，通过一系列的生化反应将信号传递到细胞核内，诱导特定基因表达，从而引起细胞生理(如分化和凋亡)上的变化[1]。大量转导路径交叉级联组成了生物信息系统，其经历了漫长的演化过程，表现出优异的生物鲁棒性[2]。即无论是外部因素的扰动或是内部参数的摄动，生物都能够保持其整体功能的可靠性与稳定性[3-5]。已有研究表明[6]，细胞信号通路对干扰有一定的抵抗能力，在一定的干扰程度下，细胞信号网络可以维持其功能鲁棒，但维持其鲁棒性的作用机制尚未明确。有研究认为生物鲁棒性的重要机制主要有代偿机制，系统控制机制，模块化设计机制和退耦机制。其中，代偿机制包括简并和冗余[3,7]。

简并性是生物中极为重要的现象，定义为系统内不同结构的部件在特定条件下具有相同功能或产生相同输出的一种属性[8]。诺贝尔生理和医学奖得主杰拉德·埃德尔曼(Gerald Edelman)在他的神经达尔文主义中首次揭示了神经系统中的简并性现象[9]，并提出了一个衡量系统简并性的指标[10]，认为这种现象广泛存在于生物系统的各级组织[11]。此外，文献[12]利用基因敲除实验证明了基因网络的简并性能够提高其变异鲁棒性；文献[13]结合神经信息编码讨论了双耳定向神经网络中简并性的表现形式和作用机理；文献[14]利用人工演化电路模拟细胞网络，证明了具有相同演化特征的细胞网络主要利用简并性提高其整体功能的鲁棒性。以上研究表明鲁棒性与简并度有一定联系，但是，关于细胞信号网络鲁棒性与简并度的定量研究少有发表。

生物网络的特性与其拓扑结构密不可分，可以利用数学建模对细胞信号网络进行抽象模拟。Kauffman在《nature》发表文章，首次将布尔网络引入生物建模，并被广泛地应用于基因调控网络的行为预测和机制研究，取得了很好的成果[15]。文献[16]综述了布尔网络在细胞网络中的应用与方法，表明布尔建模是进行细胞网络结构分析的有效手段。文献[17]利用布尔模型对细胞信号网络中的网络模体(motifs)进行建模，并研究了模体的结构与功能。文献[18]针对基因调控网络的前馈网络模型进行了布尔建模，以研究其网络特性。布尔模型是一种离散的定性网络模型[16]，在对细胞信号网络的建模过程中，蛋白质等的活性化过程存在活性阈值和超敏响应，当仅关注活性有无而不是活化过程时，网络中的蛋白质等物质可以转化为布尔节点，模拟其活性的有无，进而可以用布尔网络模拟细胞信号网络。

本文利用细胞信号网络模型探讨维持其功能鲁棒特征的拓扑简并机制，并进行量化研究。首先是利用离散的布尔网络模型进行细胞网络拓扑建模，再借助Edelman等提出的量化方法计算网络拓扑的简并性、冗余性与复杂性，进而，对比分析它们与功能鲁棒度的相关性及作用机理。

1细胞信号网络建模

1.1网络模型

建立一个细胞信号网络的布尔网络模型，需要确定网络的节点(物质)及其连接关系(相互作用)。细胞信号网络包含许多功能子网络，这些子网络同时也互相影响联系，形成一个复杂网络。为研究整个网络的特点，不应该局限于某个节点蛋白或者某个子网络，应该从系统整体的高度来进行分析，根据网络的主要结构特点，对细胞信号网络进行合理的简化，忽略掉一些对网络行为影响不大的过渡产物，把一些同工蛋白进行整合。

本研究重点针对细胞信号网络中的前馈网络通路进行研究，前馈网络是生物网络中非常简单而又通用的网络模型[18]，已被广泛应用于细胞信号网络建模[19-20]。细胞内信号通过一系列蛋白质分子的激活抑制通路，逐级向下游传递，这是细胞信号传递的一个主要特征[21]。同时，不同信号通路交叉联系，通过不同路径向下游传递，构成细胞信号网络的基本骨架结构，形成前馈网络。

采用前馈布尔网络模型，拓扑结构如图1所示。输入层节点(IN)代表细胞表面的信号感知受体，用于感受外部环境刺激；转导层节点(TS)代表细胞内的信号转导信使，用于处理和传递信号；输出层节点(OUT)代表细胞内的效应靶蛋白，对外部刺激做出响应，如调节代谢途径、调控基因表达和调整细胞性状。其中，节点间的调控关系限制为前馈连接，所有节点只能接受来自相对其前层节点的调控。

(1)

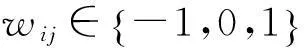
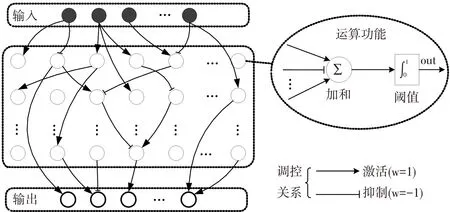
图1　前馈布尔网络拓扑模型

1.2网络拓扑演化

对于上述模型，不同的调控矩阵代表不同的网络拓扑结构，称其为结构型Gi。输出层节点在不同输入下的状态集合代表此种拓扑结构的功能(即功能真值表)，称为功能型Φi。结构型和功能型的所有可能取值组成了结构空间G和功能空间Φ，它们之间的映射关系如式2所示

(2)

其中，每一种结构型都对应于一种功能型，而每一种功能型对应于多种结构型。具有相同功能的不同网络拓扑对于变异扰动的鲁棒性也不尽相同[22]。因此，本文采用拓扑演化方法探寻结构型空间，以寻找功能鲁棒性较高的拓扑结构，并利用下一节的定量分析手段研究其维持功能鲁棒的拓扑特征与作用机制。

演化算法选用(1+λ)演化策略，且分为目标功能设计和鲁棒度优化两个阶段。

在目标功能设计流程中，首先是随机生成具有(1+λ)个结构型的种群。然后，对种群内所有结构型进行功能适应度评估，选择适应度最高的结构型为父代，判断其适应度是否达到100%。如是则进行鲁棒性能优化，否则将其变异而产生λ个子代结构型并替换原始种群内的其它结构型。循环以上过程直到演化生成适应度为100%的网络拓扑，并保存作为待优化结构型。

在鲁棒优化阶段，首先需将待优化结构型选为父代个体，父代变异生成λ个功能适应度均为100%的子代个体，组成优化种群。然后评价种群内所有结构型的功能鲁棒度，选择鲁棒度最高的个体作为父代个体，循环此过程直到最高鲁棒度在104代内没有增长。

功能适应度(Fitness, F)表示网络拓扑在所有输入状态下完成目标功能的能力，以实际功能输出与目标功能输出之间的汉明距离表示，计算方法如(3)式所示。

(3)

其中，n和m分别代表目标功能输入层和输出层的节点数，dij代表目标功能真值表中第i行、第j列的数值，yij代表实际功能真值表中第i行、第j列的数值。

功能鲁棒度(Robustness，R)表示网络拓扑受到外部或内部不确定因素的干扰时，其功能维持稳定的一种属性[7]。而生物体面临的干扰类型可归为三类：随机噪声、环境变化和基因突变[4]。对于细胞网络而言，这些干扰类型的作用点有所不同，可能影响细胞表面受体活性、第二信使扩散、基因表达和蛋白修饰等等。但是，从效应结果来看，这些干扰最终会影响布尔网络模型中节点的状态表达。本文利用恒定抑制、恒定激活或随机状态来模拟外界环境的干扰。进而，借鉴文献[3]提出的生物鲁棒性评价方法以计算本文网络模型的功能鲁棒度，如式(4)所示。

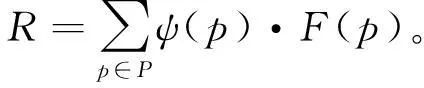
(4)

其中，P代表外界干扰对网络拓扑的干扰模式全集，函数ψ(p)代表干扰模式p发生的概率。本文假设所有网络节点以相同的概率受扰，受扰节点的3种响应形式的概率也相同。对于使用n个节点的网络拓扑，干扰模式共有3n种，每种干扰模式发生的概率为1/3n。F(p)代表网络拓扑在干扰模式p作用下的功能适应度，计算方法如式(3)所示。

2简并性的量化方法

简并性定义为系统内不同结构部件在特定条件下具有相同功能或产生相同输出的一种属性。它普遍存在于生物系统的各个层次，而没有特定的结构对象或固定的拓扑形式。因此，利用理论方法评估系统的简并性就成为认识和理解其作用的重要手段。

简并性对于网络整体功能的实现而言，不仅体现在网络内节点子集的独立贡献(个性)，还包括子集之间的协同贡献(共性)。因此，量化网络简并性时需要评估节点子集通过不同方式对网络整体功能的贡献量。本文借鉴文献[10]提出的简并度计算方法，以网络任意二分子集间的功能贡献度的重叠量计算(即所有结构子集间冗余的功能贡献度)，如式(5)所示。

(5)

由(5)式可知，简并包括了网络中任一子集与其补集之间的对整体功能贡献的重叠量。当任一子集与补集相互独立时，网络的简并性较低。而当任一子集和输出之间的互信息与其补集和输出之间的互信息相同，并且与网络整体和输出之间的互信息的值相同时，网络的简并性最高，为(N/2)·MI(X,O)。

(6)

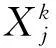
(7)

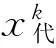
简并和冗余是两个易于混淆的概念，也是简并现象被忽视的重要原因。因此，本文在相同的评价体系下给出冗余度的计算方法，量化对比它们之间的差异性。冗余是指利用相同的部件单元完成相同的功能，代表了各单个节点对系统功能贡献的重叠量，利用所有独立节点的功能贡献量之和与网络整体贡献量的差值计算，如式(8)所示。

(8)

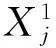
冗余和简并都反映了网络拓扑特征对输出功能的影响，而没有反映网络拓扑本身的特征属性。因此，借鉴文献[23]提出的复杂度的概念，度量细胞网络既可功能集成(所有节点共同完成功能)、又可功能分化(不同节点子集的功能相对独立)的程度。计算方法如式(9)所示。

(9)

复杂度反映了不同拓扑子集之间相互关联、功能耦合的紧密程度。当节点子集与其补集之间的互信息较低时，节点之间共享的信息熵较少且功能相互对立，网络的复杂度较低，反之亦然。

3实验结果

针对上述布尔网络模型，利用演化方法探寻了网络拓扑空间，并对其功能鲁棒性与拓扑简并性之间的相互作用关系进行了分析。实验中的网络模型输入层节点数为4，转导层节点数为28(4行×7列)，输出层节点数为3；目标功能为3输入2输出的随机布尔函数，演化结果最多含有20个网络节点；独立运行上述演化算法100次，鲁棒度优化104代。对结果进行线性拟合，以排除演化算法的随机性。

图2(a-b)分别为网络拓扑在不同演化阶段的鲁棒度与简并度和冗余度之间的线性相关性。在目标功能设计阶段(图2-a)，网络拓扑的鲁棒度最高为90%，简并度和冗余度均值分别为2.1和0.8。鲁棒度优化阶段(图2-b)的鲁棒度最高能够达到100%(简并度为4.6，冗余度为1.9)，即对于实验定义的任意干扰模式，网络的既定输出功能均不受影响。对演化结果进行统计分析，鲁棒度与简并度和冗余度的Spearman等级相关系数在目标功能设计阶段分别为0.220(p=0.043)和0.072(p=0.513)，而鲁棒度优化阶段分别为0.648(p=0)和0.506(p=0)。即在目标功能设计阶段，鲁棒度和简并度显著正相关，而鲁棒度和冗余度没有相关性；鲁棒度优化阶段，鲁棒度和简并度与冗余度均显著正相关，而相关系数简并度较冗余度大。由此可看出，简并度是和鲁棒度显著相关的指标，虽然随着鲁棒度的增长，网络的冗余度和简并度都逐渐增长，但简并度较冗余度的上升趋势更为明显，并随着鲁棒度的升高而逐渐突出。此外，对于不同演化程度的细胞网络，相比冗余度，简并度与鲁棒度的相关性更显著。

图3(a-b)分别为演化生成网络拓扑在网络拓扑演化的不同阶段的的复杂度与鲁棒度、简并度和冗余之间的线性相关性。在目标功能设计阶段，复杂度与鲁棒度的Spearman等级相关系数为0.251(p=0.021)，复杂度与简并度和冗余的Spearman等级相关系数分别为0.958(p=0)和0.767(p=0)；在鲁棒度优化阶段，复杂度与鲁棒度的Spearman等级相关系数为0.680(p=0)，复杂度与简并度和冗余的Spearman等级相关系数分别为0.974(p=0)和0.832(p=0)。由结果可知，在目标功能设计阶段和鲁棒度优化阶段，复杂度与鲁棒度均显著正相关，随着鲁棒性的提高，网络的复杂度增加，符合生物实际。简并度与复杂度正相关。相比冗余度与复杂度的相关性，简并度与复杂度显著性更强。并且对比不同演化阶段，随着演化程度的增加，简并度与复杂度相关性增加。由此可以看出，简并度相比冗余度，与复杂度的关系更加紧密，简并可以是解决生物复杂问题的有效手段。

为了进一步区分简并和冗余的作用形式，需要分析它们对网络拓扑自身属性的影响。根据图4(a)可知，鲁棒度与节点数的Spearman等级相关系数为0.676(p=0)，随着鲁棒度的线性增长，网络所需节点数呈指数增长。因为此时不仅需要节点资源完成目标功能，还需要额外的节点提高其功能鲁棒性。并且，随着鲁棒性的增长，提高鲁棒性的难度也逐渐增加。由图4(b)可以看出额外的节点资源导致网络拓扑发生的变化，结果显示网络节点数与复杂度、简并度和冗余度的Spearman等级相关系数分别为0.951(p=0)、0.933(p=0)和0.781(p=0)，网络节点数与复杂度和简并度满足较高的线性相关性，而与冗余度的相关性较低。这说明额外的节点资源以简并的方式提高了网络拓扑的复杂度，而冗余度并没有显著提高。

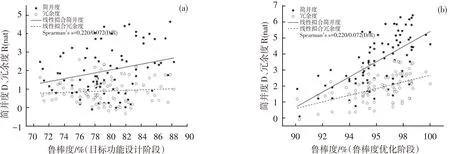
图2　演化生成网络拓扑的鲁棒度与简并度和冗余度关系

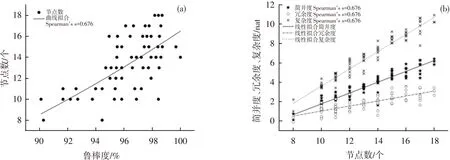
图4　演化生成网络拓扑的节点数与拓扑参数

4讨论

神经网络、基因调控网络和新陈代谢网络等生物系统中存在大量冗余单元。而这些冗余单元并不是通过简单的冗余备份来维持系统功能的稳定性，而是利用简并的方式提高系统功能的鲁棒性，同时保持系统的复杂度与演化能力[24-28]。本文使用的数值计算模型证明了细胞网络与其它生物系统相同，主要利用简并性而不是冗余来抵御外界环境干扰并维持其功能鲁棒性。并且，通过此模型能够更加深入了理解细胞网络的拓扑复杂性和简并性，以及对于鲁棒和演化特征的作用机制。在本研究中，为研究细胞信号网络的特性，对网络进行抽象为前馈网络，虽然该网络具有细胞信号传导的基本特征，但是忽略了许多细节，如反馈调控，具有一定的局限性。细胞的信号处理网络主要包括信号的接收，传导和输出响应，主要依靠蛋白质分子，基因和RNA分子通过复杂网络系统共同作用实现。信号通过一系列蛋白质分子的激活抑制通路，逐级向下游传递，连接形成前馈网络[21]。同时，不同信号通路交叉联系，局部连接形成许多反馈子网络。在未来的研究中，可以进一步优化网络建模，增加网络的复杂度。

生物简并性是指生物系统内不同结构的组分具有相同功能的特点，经常会与冗余性混淆。冗余是指完全相同的组分具有相同功能。生物系统中很少有完全相同的组分，因此冗余系统在生物系统中很少见。而简并性普遍存在于生物系统的各个层次中，如免疫系统、神经系统、细胞网络等[11]，并且已有许多学者对生物简并性做出研究，发现生物简并性与生物系统的鲁棒性、复杂性和演化性等特性密不可分。文献[24]阐述了生物系统中简并、鲁棒和复杂度的关系，认为简并是鲁棒的基础，并且在促进生物系统的鲁棒性、演化性和复杂性的形成过程中起到了关键的核心和枢纽作用。文献[10]认为在生物系统中，简并应当区别于冗余，并证明具有简并特性的神经网络同样也具有高复杂度。文献[11]指出简并是生物系统普遍存在的现象，是神经系统复杂度的一个特征表现。文献[29]研究发现在神经系统中，冗余系统具有较低的演化性而简并系统演化性较高，简并是生物系统演化和鲁棒的重要促成因素。文献[30]提出了计算生物系统简并性的一种方法，简并可以评价系统的演化性。在本研究中，细胞信号网络的简并度和鲁棒度正相关，并且随着演化程度的增加，其相关程度也增加并且高于冗余度与鲁棒度的相关性。

生物网络的拓扑简并性对维持其功能鲁棒具有重要作用，这一结果可为人工系统的仿生设计提供新思路。例如，文献[31]借鉴生物信息处理的鲁棒机制弥补传统电磁防护技术的不足，首次将仿生思想引入电磁防护领域，以提高电子系统在复杂电磁环境下的可靠性与适应能力。在作用形式上，生存环境对细胞信号网络的影响与复杂电磁环境对电子系统的干扰极为相似，都会引起系统的单元部件产生信号扰动、信息错乱乃至物理损伤的现象；而在效应结果上，这两类系统的功能鲁棒性表现迥异。因此，细胞网络维持其功能鲁棒性的内在机理为电磁防护仿生研究提供了有益的启示。

5结论

本文利用布尔网络模型模拟细胞网络的动态行为，基于演化方法探寻网络拓扑空间，分析不同网络拓扑在干扰环境下的功能鲁棒性。进而，借鉴基于信息论的计算方法分析优化结果的简并度、冗余度和复杂度等拓扑属性，对比分析它们与功能鲁棒性的相关性和作用机理。主要得到如下结论：

(1) 对于细胞信号网络拓扑，相比冗余度，简并度与鲁棒度的相关性更显著。功能鲁棒性的差异主要来自于网络拓扑的简并性。

(2)在鲁棒度提升的过程中，网络的复杂度也随之升高，简并度相比冗余度，与复杂度的相关性更加显著，这说明简并度同时提升了网络的鲁棒性与复杂性。

(3) 网络节点数与复杂度和简并度显著正相关，而与冗余度的相关性较低。说明额外的网络节点以简并的方式提高了网络拓扑的复杂度，而冗余度并没有显著提高。

参考文献(References)

[1]刘曾荣，王瑞琦，杨凌，等. 生物分子网络的构建和分析[M]. 北京：科学出版社, 2012.

LIU Zengrong, WANG Ruiqi, YANG Ling, et al. Frame and analysis of the biological molecule network[M].Beijing:Science Press, 2012.

[2]STELLING J, SAUER U, SZALLASI Z,et al. Robustness of cellular functions[J]. Cell, 2004, 118: 675-685.

[3]KITANO H. Towards a theory of biological robustness[J]. Molecular Systems Biology, 2007, 3(1): 1-7.

[4]FELIX M A, WAGNER A. Robustness and evolution: concepts, insights and challenges from a developmental model system[J]. Heredity, 2008, 100: 132-140.

[5]朱炳，包家立，应磊. 生物鲁棒性的研究进展[J]. 生物物理学报, 2007, 23(5): 357-363.

ZHU Bing, BAO Jiali, YING Lei. Progress of biological robustness[J]. Acta Biophysica Sinica, 2007, 23(5): 357-363.

[6]LEE W B, HUANG J Y. Robustness and topology of the yeast cell cycle Boolean network[J]. FEBS Letters, 2009，583(5): 927-932.

[7]KITANO H.Biological robustness[J]. Reviews, 2004,5(11): 826-837.

[8]MASON P H. Degeneracy at multiple levels of complexity[J]. Biological Theory, 2010, 5(3): 277-288.

[9]EDELMAN G M, TONONI G. A universe of consciousness[M] . New York,NY,US:Basic Books, 2000.

[10]TONONI G, SPOMS O, EDELMAN G M. Measures of degeneracy and redundancy in biological networks[J]. PNAS, 1999, 96(6): 3257-3262.

[11]EDELMAN G M, JOSEPH A. GALLY J A. Degeneracy and complexity in biological systems[J]. PNAS, 2001, 98(24): 13763-13768.

[12]WAGNER A. Distributed robustness versus redundantcy as cause of mutational robustness[J]. BioEssays, 2005, 27(2): 176-188.

[13]张宏，刘淑芳，钱鸣奇，等. 神经系统的简并性与序空间编码分析[J]. 物理学报, 2009, 58(10): 7322-7328.

ZHANG Hong, LIU Shufang, QIAN Mingqi, et al.Analyses of degeneracy in neural system and neural code[J]. Acta Physica Sinica, 2009, 58(10): 7322-7328.

[14]MACIA J, SOLE R V. Distributed robustness in cellular networks: insights from synthetic evolved circuits[J]. Journal of the Royal Society Interface, 2009, 6(33): 393-400.

[15]KUAUFFMAN S. Homeostasis and differentiation in randam genetic control networks[J].Nature,1969,224:177-178.

[16]WANG R S, SAADATPOUR A, ALBERT R. Boolean modeling in systems biology: an overview of methodology and applications[J]. Physical Biology, 2012,9:1-14.

[17]TYSON J, NOVAK B. Functionalmotifs in biochemical reaction networks[J]. Annu. Rev. Phys. Chem, 2010,61: 219-240.

[18]FEMRNANDEZ P, SOLE R V. Neutral fitness landscapes in signalling networks[J]. J. R. Soc. Interface, 2007,4:41-47.

[19]BRAY D. Protein molecules as computational elements in living cells[J]. Nature, 1995,376:307-312.

[20]WENG G, BHALLA U S, IYENGAR R. Emergent properties of networks of biological signaling pathways[J]. Science, 1999, 283(5400):381-387.

[21]孙大业，郭艳林，马力耕，等. 细胞信号转导[M].北京：科学出版社, 2001.

SUN Daye, GUO Yanlin, MA Ligeng, et al. Cellular signal transduction[M].Beijing:Science Press, 2001.

[22]WAGNER A. Robustness and evolvability: a paradox resolved[J]. Proceedings of the Royal Society B, 2007, 275(1630): 91-100.

[23]TONONI G, EDELMAN G M, SPORNS O. Complexity and coherency: integrating information in the brain[J]. Trends in Cognitive Science, 1998, 2(12): 474-484.

[24]WHITACRE J M. Degeneracy: a link between evolvability, robustness and complexity in biological systems[J]. Theoretical Biology and Medical Modelling, 2010, 7(6): 1-17.

[25]WHITACRE J M, ROHLFSHAGEN P, BENDER A, et al. Evolutionary mechanics: new engineering principles for the emergence of flexibility in a dynamic and uncertain world[J]. Natural Computing, 2012, 11(3): 431-448.

[26]RANDLES M, LAMB D, ODAT E, et al. Distributed redundancy and robustness in complex systems[J]. Journal of Computer and System Sciences, 2011, 77(2): 293-304.

[27]DEMONGEOT J, WAKU J. Robustness in biological regulatory network III: Application to genetic networks controlling the morphogenesis[J]. Comptes Rendus Mathematique, 2012, 350(5): 289-292.

[28]JAMES M W. Biological robustness: paradigms, mechanisms and systems principles[J]. Frontiers in Genetics,2012,3:1-15.

[29]WHITACREA J, BENDER A. Degeneracy: a design principle for achieving robustness and evolvability[J]. Journal of Theoretical Biology, 2010,263(1):143-153.

[30]LI Y, DWIVEDI G, HUANG W,et al. Quantification of degeneracy in biological systems for characterization of functional interactions between modules[J]. Journal of Theoretical Biology, 2012, 302: 29-38.

[31]刘尚合，原亮，楮杰. 电磁仿生学--电磁防护研究的新领域[J]. 自然杂志, 2009, 31(1): 1-7.

LIU Shanghe, YUAN Liang, CHU Jie.Electromagnetic Bionics: A New Study Field of Electromagnetic Protection[J]. Chinese Journal of Nature, 2009, 31(1): 1-7.

*通信作者：岳训，男，副教授，硕士生导师，研究方向：计算系统生物学，生物信息学，数据挖掘；E-mail:yuexun@sdau.edu.cn.