混沌特征量识别切削颤振的试验研究

第一作者毛汉颖男，副教授，1968年生

通信作者毛汉领男，博士，教授，博士生导师，1963年生

混沌特征量识别切削颤振的试验研究

毛汉颖1，刘畅2，刘永坚2，毛汉领2

(1. 广西科技大学汽车与交通学院，广西柳州542506；2. 广西大学机械工程学院，南宁530004)

摘要：针对切削颤振具有的非线性，传统信号处理方法不能全面揭示颤振特征及难以识别预报等问题，通过改变切削速度及深度的多组切削试验，获得从平稳切削到颤振状态完整过程的多组振动加速度信号，采用关联维数、最大Lyapunov指数及Kolmogorov熵等分析测试信号的混沌特征。结果表明，三个混沌特征量均能从不同角度较好揭示切削过程从平稳到颤振的变化规律。多混沌特征可能将是识别预报颤振的新方向。

关键词：切削；颤振；混沌特征；识别

基金项目：国家自然科学基金(51365006,51445013)；南宁市科技计划项目(20131067,20130950)

收稿日期：2014-12-31修改稿收到日期：2015-01-04

中图分类号:TG51文献标志码：A

Experimental study on the identification of cutting chatter based on its chaotic characteristics

MAOHan-ying1,LIUChang2,LIUYong-jian2,MAOHan-ling2(1.College of Automobile and Transportation,Guangxi University of Science and Technology, Liuzhou 542506，China；2. College of Mechanical Engineering, Guangxi University, Nanning 530004，China)

Abstract:Because the cutting chatter is a nonlinear behavior, it is difficult to identify and predict the chatter phenomenon with the traditional signal processing method. A number of groups of cutting tests were designed and made under different spindle speeds and cutting depths. The vibration acceleration signals of the whole process from stable cutting to chatter were detected. The chaotic characteristics of the signals were analyzed by virtue of the correlation dimension, largest Lyapunov exponent and Kolmogorov entropy. It is demonstrated that the evolution of a sharp rise during chatter gestation can be revealed by all the three chaotic characteristics individually. The multi chaotic characteristics analysis might be the new direction for the identification and prediction of the cutting chatter.

Key words:cutting; chatter; chaotic characteristics; identification

颤振为金属切削过程中因刀具与工件间自激振动引起的异常状态。1907年Taylor首次提出并阐述切削颤振的产生及主要原因；Arnold等提出并完善颤振的负摩擦理论；Tusty提出切削机床颤振振型耦合理论；Hahn提出再生型切削颤振机理；土井静雄等提出滞后型颤振机理；Tobias等利用线性理论对切削颤振稳定性进行分析；Tlusty等在线性切削范围内进一步研究颤振机理，形成再生型、振型耦合及摩擦型等颤振机理模型；星铁太郎提出混合型颤振概念，认为混合型切削颤振由外部激励与再生效应共同作用结果[1-2]；杨叔子等提出切削颤振非线性理论模型，通过建立切削颤振非线性函数，揭示影响切削颤振的非线性因素；陈花玲等建立迟滞非线颤振模型；于骏一等用振动波形不规则系数及似然比统计量对颤振进行预报研究；黄强等揭示切削加工从稳定切削到颤振切削过渡过程特性；高国利等建立预报切削颤振的切削力二阶时序模型等。颤振产生原因及发生、发展规律与切削过程本身及切削机床动态特性存在本质联系，为极复杂的机械振动现象，颇受关注。

通过切削试验及传感检测技术拾取切削过程中振动、切削力、噪声或声发射等信号，利用适合的信号分析与处理手段提取表征颤振预兆的特征量进行颤振识别预报研究。如 Kim[3]基于铣削过程动态切削力模型，对切削力信号进行频谱分析，识别数控铣床中的颤振；Cardi[4]提出用切削力及切屑流出速度相位差提前识别颤振；Somkiat[5]将车削动态切削力的三个分量各自互功率谱函数用于研究颤振频率并识别颤振。迄今，识别颤振研究多为单值线性，但多参数值识别预报应较单值能更有效避免颤振的漏判、误判。提高切削颤振识别预报的容错能力及判别速度受到高度重视。如Tarng[6]用自适应推理(ART2-A)神经网络方法研究钻削中颤振识别；孔繁森等[7]研究基于试验数据经验分布与颤振信号理论分布贴近度的颤振识别模糊系统；陈展翼等[8]用加工过程中铣削力、振动信号功率谱及能量变化比识别颤振；李峥等[9]通过测量切削过程中产生的噪声进行时、频域分析识别颤振；吕凯波等[10]用时域方差及频域谱特征作为颤振发生的综合指标，对比研究颤振切削及正常切削。

切削颤振为非线性过程，检测的各种信号具有非线性。传统的线性理论分析方法不能较好识别、预测颤振，非线性分析方法应能全面完整揭示颤振本质。Canales等[11]发现铣削振动信号近似熵随机性指数能较好反映铣削过程的稳定性而提出颤振监测新方法；吴石等[12]通过对铣削振动信号的盒维数及近似熵分析，实现对颤振征兆识别；Wang等[13]通过关联维数及最大Lyapunov指数对再生型切削颤振的两模型中混沌现象进行对比分析，发现两模型关联维数及最大Lyapunov指数具有明显的可分性；刘鹏等[14]给出Lyapunov指数及Kolmogorov熵(K熵)与切削加工参数的关系曲线，通过该曲线监测切削颤振。尽管诸多研究采用Lyapunov指数、关联维数、K熵等分析某些颤振模型下的混沌特性，但仅对颤振、无颤振进行对比，未对从平稳切削至颤振整个过程特征量变化趋势进行分析，且采用单一指标，不能准确反映切削过程本质。因此，如何更准确揭示切削颤振特征、更好提高适应性及预报速度，由单值线性转向多参数融合的非线性识别预报，仍为研究热点及方向。

本文利用CA6140机床及MDR-80振动测试系统搭建实验平台进行多组切削试验。在不同切削速度下改变切削深度，测试从平稳切削到颤振全过程振动加速度信号，求出信号关联维数、最大Lyapunov指数及K熵，通过三个混沌特征量研究揭示颤振征兆，为多混沌特征识别、预报颤振奠定基础。

1混沌特征量

1.1关联维数

关联维数作为分形维数的一种较盒维数更适合描述复杂分形问题，且计算量小，工程中多用于描述系统的复杂程度[15]。计算关联维数主要用G-P算法，步骤为：先对一维时间序列进行相空间重构，在重构的相空间中取一个相点作为中心，以小距离r为半径作超球体，统计落在超球体内的相点数目并计算关联积分，即

(1)

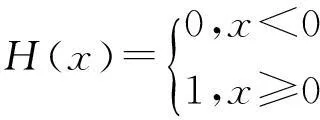
关联积分表示相空间中距离小于r的点对在所有点对中所占百分比。r足够小时关联维数逼近式为

(2)

计算时使超球体中先含少部分相点，再逐渐增加r至饱和状态绘出理想lnC(r,m)-lnr曲线，选曲线中线性性质较好部分对应的r为无标度区，该部分曲线对应的斜率即为饱和关联维数值，能反映混沌吸引子空间结构及复杂程度，因此能较好反映时间序列中隐藏的系统非线性性质信息[16]。此外，其对系统的复杂程度非常敏感，系统越不稳定关联维数越高。

1.2最大Lyapunov指数

该指数描述初始时刻距无限近两点随时间按指数方式分离特征，作为混沌运动特征量，表示相轨迹发散至覆盖整个吸引子快慢及对初始值的敏感程度[17]。

设时间序列为{x1,x2,…,xN}，N为时间序列长度。对时间序列进行相空间重构的相空间轨迹为

Xi={xi,xi+τ,…,xi+(m-1)τ}

(3)

式中：i=1,2,…,M,M=N-(m-1)τ，m为嵌入维数，τ为时间延迟。

最大Lyapunov指数计算步骤为在相空间中寻找给定轨迹上每个点的最近邻点，即

(4)

式中：p为时间序列平均周期。

计算轨道上每个点及最近邻点的分离速率，据此求出最大Lyapunov指数，即

(5)

最大Lyapunov指数大于0说明振动处于混沌状态，等于0说明处于稳定周期运动状态。

1.3K熵

K熵为将信息熵概念进一步精确化获得结果，用于描述系统运动混乱或无规则程度。最大似然算法为：初始邻近点间距离由无限小分离至大于给定距离r0，所经时间满足指数分布，即

c(t0)=e-Kbτs,(b=1,2,3,…)

(6)

式中：τs为时间序列采样间隔；b为初始邻近点之间距离首次超过r0时经历的演化步数。

在b个时间步长演化后，初始邻近点之间距离大于r0的概率为

P(b)=c(b-1)-c(b)=(e-k-1)e-kb

(7)

式中：k=Kτs。

将概率密度函数作归一化处理，在相空间中取出Q对不相关点，得似然函数为

(8)

S(k)最大值即为K熵最大似然估计量。由K熵大小可区别混沌运动、随机运动及规则运动。K熵为0对应规则运动；无界对应随机运动；大于0对应混沌运动。K熵越大信息损失速率越高，系统混沌程度越严重[18]。

2切削实验

2.1实验系统组成

整个实验平台见图1。实验机床为CA6140机床，试验工件为长240 mm、直径40 mm的45号钢圆柱形棒料，用YT15硬质合金机夹刀加工，三向加速度传感器为604B11/M006JW固定于刀杆测量振动加速度，数据采集用MDR-80移动数据记录器。切削试验时三向加速度传感器将机械振动信号转换成模拟电信号，经低通抗混滤波器滤波、MDR-80内部调理器及A/D转换器处理后转换成数字信号，传送至计算机，用MATLAB软件及计算程序对数据进行分析处理。

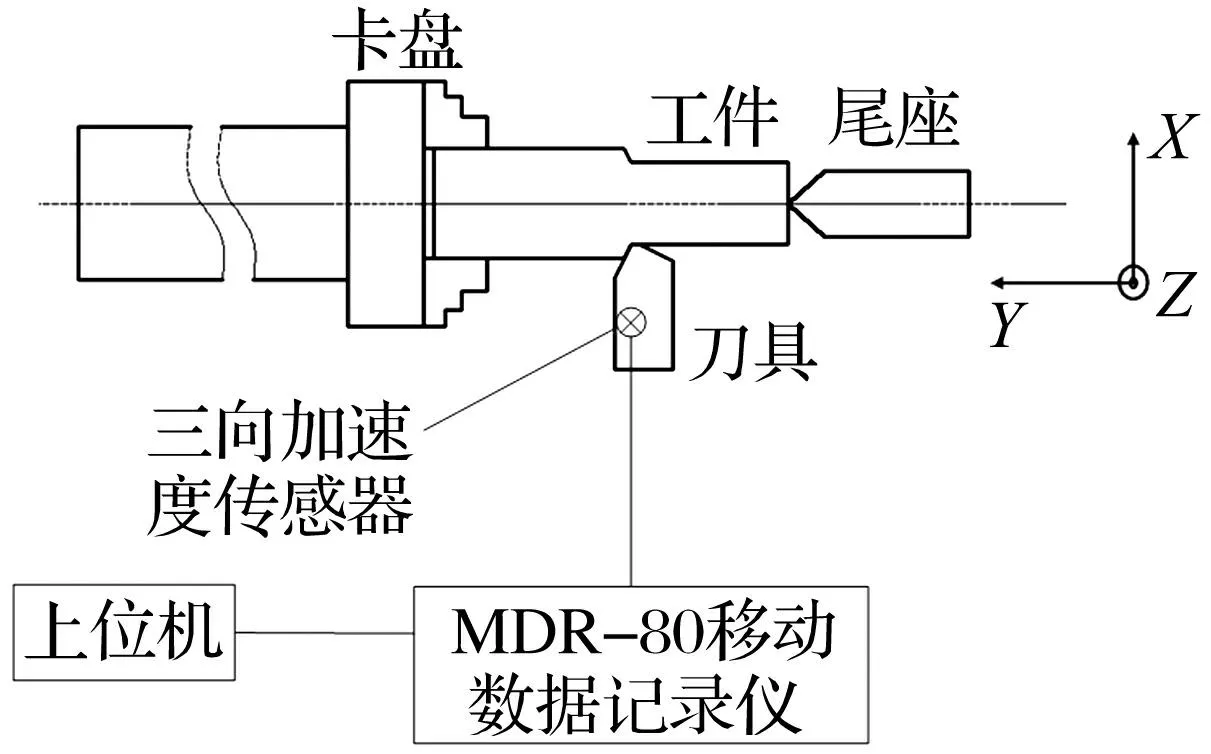
图1　机床颤振实验平台 Fig.1 Experimental platform of machine tool chatter

2.2实验参数

测试装置参数设置见表1，通讯接口为网口。

表1　数据测试参数

试验中切削用量设为Y轴方向刀具进给速度0.16 mm/r，在各主轴转速下分别改变切削深度进行切削，具体设置见表2。各主轴转速下最后切深时发生强烈颤振、不能切削。按表2分别进行三种不同转速下多种切削深度试验，由MDR-80测试系统，按表1各项参数检测、记录每次的振动加速度信号。

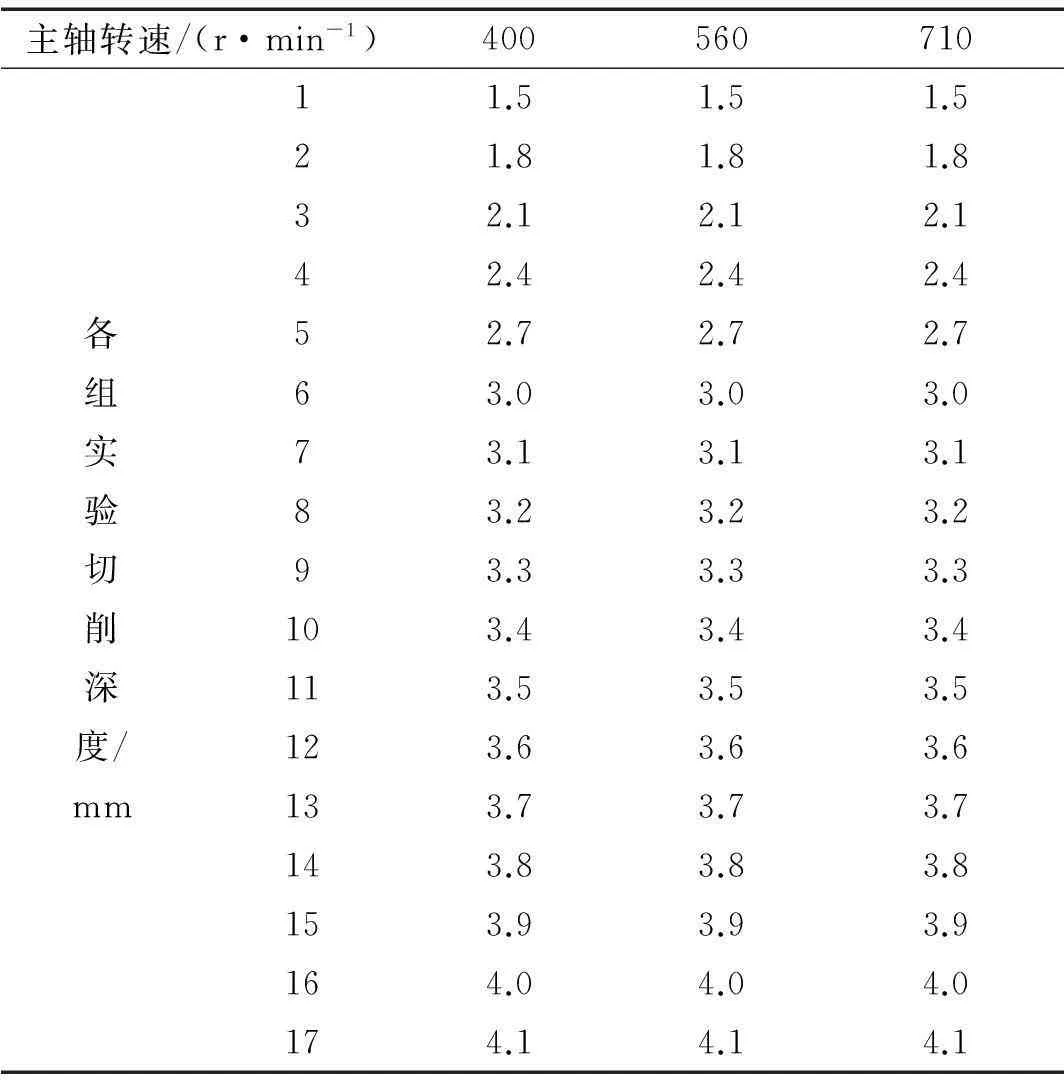
表2　主轴不同转速下切削深度(mm)

3实验数据分析

正常切削时刀具处Z向振动加速度幅值在5 m/s2附近波动，振动幅度并不大，切削处于较平稳状态；切削深度达到4.1 mm时出现颤振现象，振动加速度幅值变大，变化范围为30～40 m/s2，部分甚至超过40 m/s2，说明颤振发生时振动幅度明显增大，机床切削由稳定状态进入不稳定状态。与Z向类似，刀具处X向振动加速度幅值在0～5 m/s2范围内变化，颤振切削时振动加速度变化范围增大至20 m/s2。

3.1关联维数计算及结果分析

用G-P法获得转速为400 r/min、560 r/min、710 r/min时不同切深下的关联维数，见图2。由图2各转速下X，Z向关联维数随切深变化关系看出，切削深度较小时关联维数呈稳定状态，数值稳定在4.3附近，说明开始切削阶段振动信号稳定性未发生明显改变；随切削深度不断增加，达到临近颤振状态的几组切深时，关联维数急剧增加并在颤振发生时达最大值，说明接近颤振切深时振动信号的稳定性迅速下降；通过观察关联维数是否突然增大可对切削颤振进行预报。因尚无确切的度量标准衡量关联维数值变化率，据该参数无法准确预报颤振。

图2　各转速下X，Z向关联维数计算结果 Fig.2 The correlation dimension of X and Z direction under different cutting depths and spindle speeds

3.2最大Lyapunov指数计算及结果分析

用相空间法计算获得400 r/min、560 r/min、710 r/min时不同切深下振动信号最大Lyapunov值，见图3。由图3最大Lyapunov指数随切削深度变化曲线看出，最大Lyapunov指数始终大于0，说明平稳切削与颤振切削时均存在混沌现象。切深较小时最大Lyapunov指数呈缓慢增加趋势，接近颤振的几组切削深度下，最大Lyapunov指数曲线斜率变化明显增大，说明在颤振孕育阶段振动信号对初始值敏感性显著增强；颤振发生时最大Lyapunov指数出现一定程度下降，说明颤振孕育阶段振动信号混沌程度最高。因此，据最大Lyapunov指数变化规律可实现对颤振的预报。

图3　各转速下X，Z向最大Lyapunov指数计算结果 Fig.3 The largest Lyapunov exponent of X and Z direction under different cutting depths and spindle speeds

3.3K熵计算及结果分析

用最大似然法计算各组振动加速度序列K熵，获得转速为400 r/min、560 r/min、710 r/min时不同切深下试验振动信号K熵值，见图4。由图4的K熵与切深关系曲线看出，整个切削过程K熵均大于0，说明无论平稳切削或颤振切削均存在混沌振动。切削深度较小时K熵呈总体增加趋势，数值由0.03缓慢增至0.05，颤振发生前出现突增趋势，颤振出现时K熵略有下降但仍高于平稳切削时水平。说明切削过程稳定性微小改变会显著反映在K熵值上，K熵可用于切削状态的度量标尺。K熵规律与最大Lyapunov指数类似，在颤振发生前出现先升后降的跳变规律，可据此对颤振进行预报。

图4　各转速下X，Z向K熵计算结果 Fig.4 The K entropy of X and Z direction under different cutting depths and spindle speeds

4结论

(1)机床平稳切削时振动信号会呈现较弱的混沌特征,颤振现象发生时混沌特征明显增强，其加速度信号具有混沌特征原因为切削颤振的非线性。不同混沌特征含不同非线性信息，关联维数、最大Lyapunov指数及K熵分别能描述吸引子的空间结构、系统对初值敏感性及系统混乱程度。

(2)通过总结三个混沌特征量计算方法，搭建实验平台，在不同转速及多种切削深度条件下进行切削试验，获得从平稳切削到颤振状态全过程的多组振动加速度信号；由分析知，颤振前关联维数出现急剧上升，最大Lyapunov指数、K熵呈先升后降趋势，初步揭示出从平稳切削至颤振的变化规律。

参考文献

[1]师汉明.金属切削理论及其应用新探[M]．武汉:华中科技大学出版社，2003

[2]唐英,张大勇.切削颤振研究的关键技术与进展综述[J]．工具技术,2011,45(8):9-14

TANG Ying, ZHANG Da-yong.The summary on the key technique for the cutting chatter research[J].The Tools Technology, 2011,45(8):9-14.

[3]Kima S J. Prediction of chatter in NC machining based on a dynamic cutting force model for ball end milling[J]. International Journal of Machine Tools & Manufacture, 2007, 48(47): 1827-1838.

[4]Cardi A A. Workpiece dynamic analysis and prediction during chatter of turning process[J]. Mechanical Systems and Signal Processing, 2008, 35(22): 1481-1494.

[5]Charoen S T. In-process monitoring and detection of chip formation and chatter for CNC turning[J]. Journal of Materials Processing Technology,2009,209(56):4682-4688.

[6]Tarng Y S. On-line drilling chatter recognition and avoidance using an ART2-A neutral network[J] . Int. J. Mach. Tools Manufacture, 2002, 13(7): 949-957.

[7]孔繁森,于骏一,勾治践.颤振状态的模糊识别[J].振动工程学报, 1998,13(3):328-332.

KONG Fan-sen,YU Jun-yi, GOU Zhi-jian. Fuzzy identification for the chatter status[J].Journal of Vibration Engineering, 1998,13(3):328-332.

[8]陈展翼,袁军堂,汪振华,等，高速铣削颤振识别和稳定性预测[J]. 传感器与微系统, 2013, 32(3):59-61.

CHEN Zhan-yi, YUAN Jun-tang,WANG Zhen-hua, et al. Chatter identification and stability prediction for the high speed milling[J].Transducer and Microsystem,2013,32(3): 59-61.

[9]李峥,刘强.基于切削噪声测试的数控加工颤振识别系统[J].制造技术与机床, 2009 (2):16-18.

LI Zheng, LIU Qiang.The chatter identification system for the digital control processing based on the cutting noise detection[J].Manufacture and Machine Tools, 2009(2):16-18.

[10]吕凯波,景敏卿,张永强,等.一种切削颤振监测技术的研究与实现[J].西安交通大学学报, 2011, 45(11): 95-99.

LÜ Kai-bo,JING Min-qing,ZHANG Yong-qiang,et al.The research and realization of a chatter monitoring technology [J]. Journal of Xi’an Jiaotong University, 2011, 45(11): 95- 99.

[11]Pérez-Canales D,Vela-Martínez L,Carlos Jáuregui-Correa J, et al. Analysis of the entropy randomness index for machining chatter detection[J]. International Journal of Machine Tools and Manufacture, 2012, 62: 39-45.

[12]吴石,刘献礼,肖飞. 铣削颤振过程中的振动非线性特征试验[J].振动、测试与诊断, 2012, 32(6): 935-940.

WU Shi, LIU Xian-li, XIAO Fei.The test for the nonlinear characteristics on the milling chatter[J].Vibration, Detection and Diagnosis, 2012, 32(6): 935-940.

[13]Wang X S, Hu J, Gao J B. Nonlinear dynamics of regenerative cutting processes-comparison of two models [J]. Chaos, Solitons & Fractals, 2006, 29(5): 1219-1228.

[14]孔繁森,刘鹏,王晓明. 切削振动加速度时间历程演化过程的动力学特征[J].振动与冲击, 2011,30 (7): 10-15.

KONG Fan-sen, LIU Peng, WANG Xiao-ming. The dynamic characteristics of the vibration acceleration in the cutting[J].Vibration and Shock, 2011,30 (7): 10-15.

[15]汪慰军,吴昭同.关联维数的计算及其在大机组故障诊断中的应用[J].上海交通大学学报, 2000, 34(9): 1265-1268

WANG Wei-jun, WU Zhao-tong.The relative dimension calculation and application on the diagnosis of the big power generator[J].Journal of Shanghai Jiaotong University, 2000, 34(9):1265-1268.

[16]张征凯,薛松,张优云.基于特征参数的旋转机械智能故障诊断方法[J].振动、测试与诊断, 2009, 29 (3):256-260.

ZHANG Zheng-kai, XUE Song, ZHANG You-yun.The intelligent diagnosis method for the rotary machine based on the characteristic parameters[J]. Vibration, Detection and Diagnosis, 2009, 29 (3):256-260.

[17]杨智春,张蕊丽.基于最大李雅普诺夫指数的壁板热颤振特性分析[J].西北工业大学学报, 2009, 27(6): 770-776.

YANG Zhi-chun, ZHANG Rei-li.The chatter analysis of the wallboard based on Lyapunov exponent[J].Journal of Northwest Industry University, 2009, 27(6):770-776.

[18]余波,李应红,张朴.关联维数和Kolmogorov熵在航空发动机故障诊断中的应用[J].航空动力学报, 2006, 21(1): 219-224.

YU Bo,LI Ying-hong, ZHANG Pu.The application of the relative dimension and Kolmogorov entropy in the diagnosis for the aero-engine[J].Journal of the Aero-Power, 2006,21(1):219-224.