多联连续梁桥快速 MPA 方法

第一作者曹飒飒男，博士生,1982年生

通信作者袁万城男，博士,研究员,博士生导师,1962年生

多联连续梁桥快速MPA方法

曹飒飒1,2， 钟剑1， 袁万城1

(1.同济大学土木工程防灾国家重点实验室，上海200092； 2.广州大学土木工程学院，广州510006)

摘要：提出针对多联连续梁桥的快速MPA方法。通过等位移准则计算控制点目标位移，结合MPA方法进行多联连续梁桥快速多模态推倒分析，能极大简化多模态推倒分析步骤。以某3联连续梁桥为例，将等位移准则计算的控制点位移近似作为多模态推倒分析目标位移，用快速MPA方法对其抗震性能进行评估。与非线性动力时程分析结果对比表明，快速MPA方法可有效评估多联连续梁桥抗震性能。

关键词：等位移准则；多联连续梁桥；多模态推倒分析；目标位移

基金项目：国家自然科学基金(51478339，51278376);土木工程防灾国家重点实验室基金(SLDRCE14-B-14)

收稿日期：2014-05-14修改稿收到日期：2014-08-14

中图分类号:U442.5+5文献标志码：A

Rapid MPA method for multiple multi-span continuous bridges

CAOSa-sa1,2,ZHONGJian1,YUANWan-cheng1(1. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China；2. College of Civil Engineering, Guangzhou University, Guangzhou 510006, China)

Abstract:Rapid MPA method was proposed for multiple multi-span continuous bridges. In the rapid MPA, target displacements at control points were computed according to the rule of equal displacement, so the rapid MPA method can greatly simplify the procedure of MPA. For multiple multi-span continuous bridges, the control points’ displacements computed in accordance with the equal displacement rule were used as the approximation of modal pushover target displacements. The rapid MPA proposed has been carried out for seismic performance evaluation of the bridges. Compared with the time-history analysis, it turns out that the rapid MPA is capable of providing reasonable seismic responses of multiple multi-span continuous bridges.

Key words:equal displacement rule; multiple multi-span continuous bridges; rapid modal pushover analysis rapid (MPA); target displacement

桥梁结构初步设计阶段，由静力计算及抗震构造措施拟定的结构体系并非最佳抗震方案。此阶段对计算结果精度要求不高，但方案修改频繁，设计周期紧迫，因此对桥梁结构抗震性能评估的简化计算方法进行研究具有重要意义。非线性动力时程分析方法计算结果精确，但需耗费较多计算时间。推倒分析方法虽计算精度稍差，但计算速度快，可较好满足初步设计阶段要求。

众多推倒分析方法中多模态推倒分析(MPA)法优势突出：考虑高阶振型影响，且计算过程无需计算各阶模态实时动力特性，用SAP2000、MIDAS等即可实施[1]，较适合桥梁结构抗震性能评估。Kappos等[2-4]将MPA方法引入桥梁结构的抗震性能评估，研究应用所需修改及适用性、精度；且对MPA方法进行改进，以结构发生塑形变形后形状代替弹性模态形状进行推倒分析，计算效果更好，且计算方法对控制点选取依赖性更小。魏标等[5-6]以4跨带桥台的连续梁桥为背景，研究MPA方法评估非规则梁桥地震位移需求的具体细节。陈星烨等[7]提出修改的MPA方法用于对连续刚构桥抗震性能分析。

美国Caltrans规范[8]对桥梁抗震设计时通常对基本周期在0.7～3 s间桥梁结构用等位移准则。郭磊[9]通过研究国内外等位移准则的适用周期，结合我国四类场地特征周期，建议以0.7 s作为等位移准则在桥梁结构中应用的周期限值。

文献[10]通过讨论等位移准则在连续梁桥中的适用范围，将其用于评估多自由度连续梁桥横桥向位移需求；并将等位移准则从单自由度体系延伸到多自由度连续梁桥，认为当连续梁桥主要振型周期均大于单自由度等位移准则的周期下限、且主要振型质量参与系数之和超过90% 时，可以弹性反应谱分析位移近似作为连续梁桥弹塑性位移需求。延性设计的连续梁桥中，主要振型周期一般均大于0.7 s，等位移准则适用范围较广；但对连续梁桥抗震性能评估而言，梁体弹塑性位移仅为需评估的响应之一，其它如桥墩塑性铰区域剪力、桥墩塑性铰转角、承台底弯矩(用于评估桩基内力)、系梁内力及变形等仍需计算。而MPA方法可计算该响应量。

本文选取等位移准则适用的多联连续梁桥为研究对象(即主要振型周期均大于0.7 s的连续梁桥)，简要介绍基于等位移准则的快速MPA方法，结合某3联连续梁桥研究快速MPA方法的有效性及适用性。

1基于等位移准则的快速MPA方法

多联连续梁桥多模态推倒分析中，一般选各阶模态形状中位移最大节点为控制点，每阶模态对应不同控制点，每个控制点总位移响应主要由与该控制点相应阶模态控制。反之，可近似将控制点总位移响应作为与控制点相应阶模态的贡献即目标位移，即可将各控制点弹塑性位移响应作为目标位移。

对可用等位移准则的多联连续梁桥而言，连续梁桥各控制点弹塑性位移需求可由反应谱分析计算获得。取反应谱方法计算的各控制点位移作为目标位移可省去多模态推倒分析的诸多步骤(推倒分析曲线双折线化、单自由度体系目标位移计算及将单自由度体系目标位移转化为多自由度体系目标位移等)，使MPA方法得到很大程度简化。

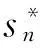
MPA方法大部分计算量均为计算各阶模态目标位移。基于等位移准则的快速MPA方法以5%阻尼比反应谱分析计算各控制点位移，取代多模态推倒分析中①～⑥，使MPA方法计算过程大大简化，故称为快速MPA方法。

2工程背景

所选某3联连续梁桥每边跨向外延伸一联作为边界联。5联主线桥跨径布置为3×31+(31+31.7+31)+(41+68+41)+3×31+(30.5+33+30.5) m，每3跨为一联，见图1。主梁采用预应力混凝土现浇箱梁，箱梁顶宽25.5 m，第3联主梁变高度、梁底变宽设计(墩顶3.8 m，跨中2 m)，其它联主梁高度不变(2 m)。梁体采用沿截面重心的单根框架单元模拟，据梁截面形状计算截面特性。梁体单元用弹性单元模拟，不计其非线性。桥墩为上部外伸的双柱式，墩高均约20 m。大跨度处(P54、P55)墩底截面2 m×1.8 m，墩轴间距5.2 m；其它墩底截面1.7 m×1.6 m，墩轴间距5.4 m。该连续梁支座布置见图2，每个墩与主梁在横桥向固定，纵桥向每联有一个固结墩。、、及○分别代表双向、纵向、横向活动及固定支座。

图1　某3联连续梁桥(m) Fig.1 A multi-span continuous bridge

图2　梁底支座布置图 Fig.2 Bearing arrangement

桩基础采用六弹簧单元进行模拟。在每个桥墩底、横系梁两端用纤维铰模拟墩非线性行为，纤维网格尺寸近似取0.1 m。纤维铰长度据经验公式[11]计算。将承台简化为质量块，置于承台中心。

据《城市桥梁抗震设计规范》[12]确定该桥E2(50年超越概率2%)抗震设防水准反应谱，其特征周期为0.4 s。采用SIMQKE随机生成与E2设计反应谱对应的3条人工地震波。3条地震波反应谱与设计反应谱对比见图3。由图3可见，人工地震波与设计反应谱拟合得较好，能有效反应场地在预定超越概率下的地震动水平。

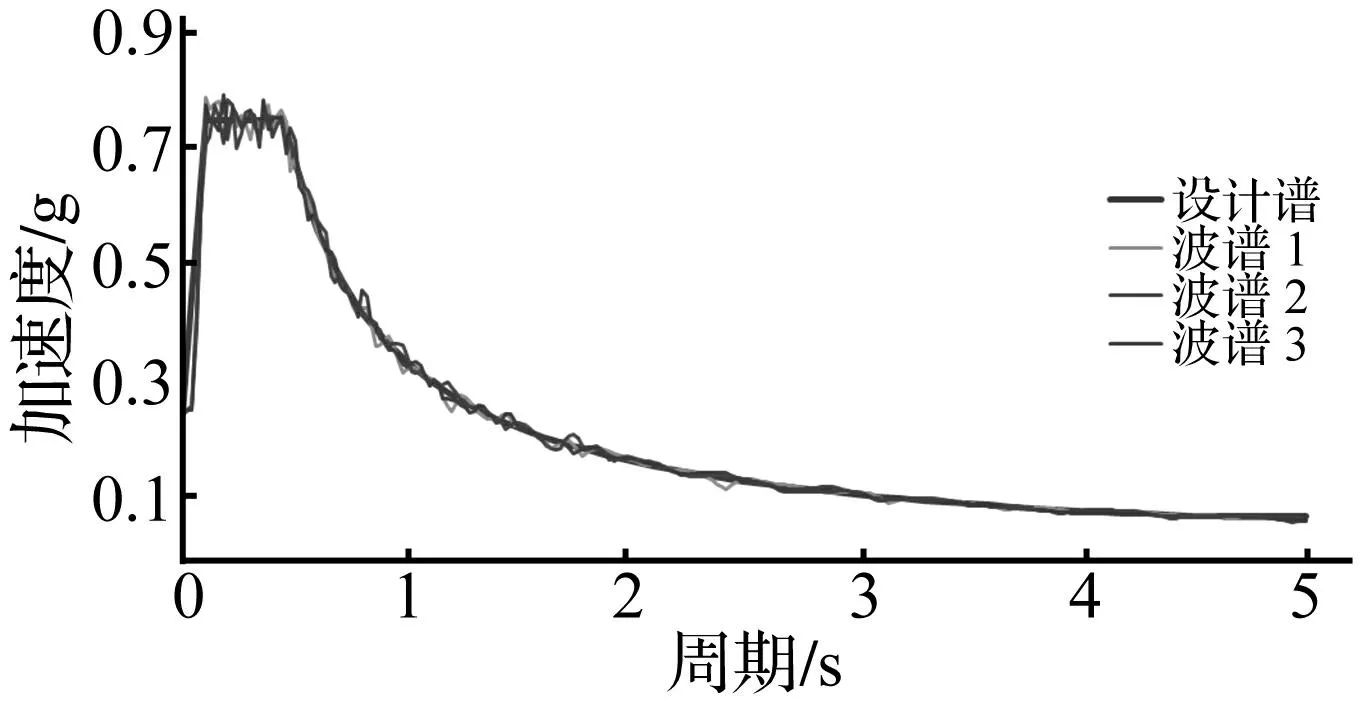
图3　设计反应谱及人工地震波反应谱 Fig.3 Design spectrum and spectra of artificial accelerograms

既有关于桥梁结构的MPA方法，桥梁两端延伸至桥台[4,13]，据桥台实际情况对梁端进行约束。桥梁总长不大、联数不多时可采用该做法；但桥梁联数较多、总长较大，而所选进行抗震性能评估的联数较少时，以上做法明显耗时费力。本文采取与非线性时程分析类似方法，将进行抗震性能评估的几联桥梁向外延伸一联作为边界联，边界联以外结构不考虑。用SAP2000软件建立有限元模型，见图4。

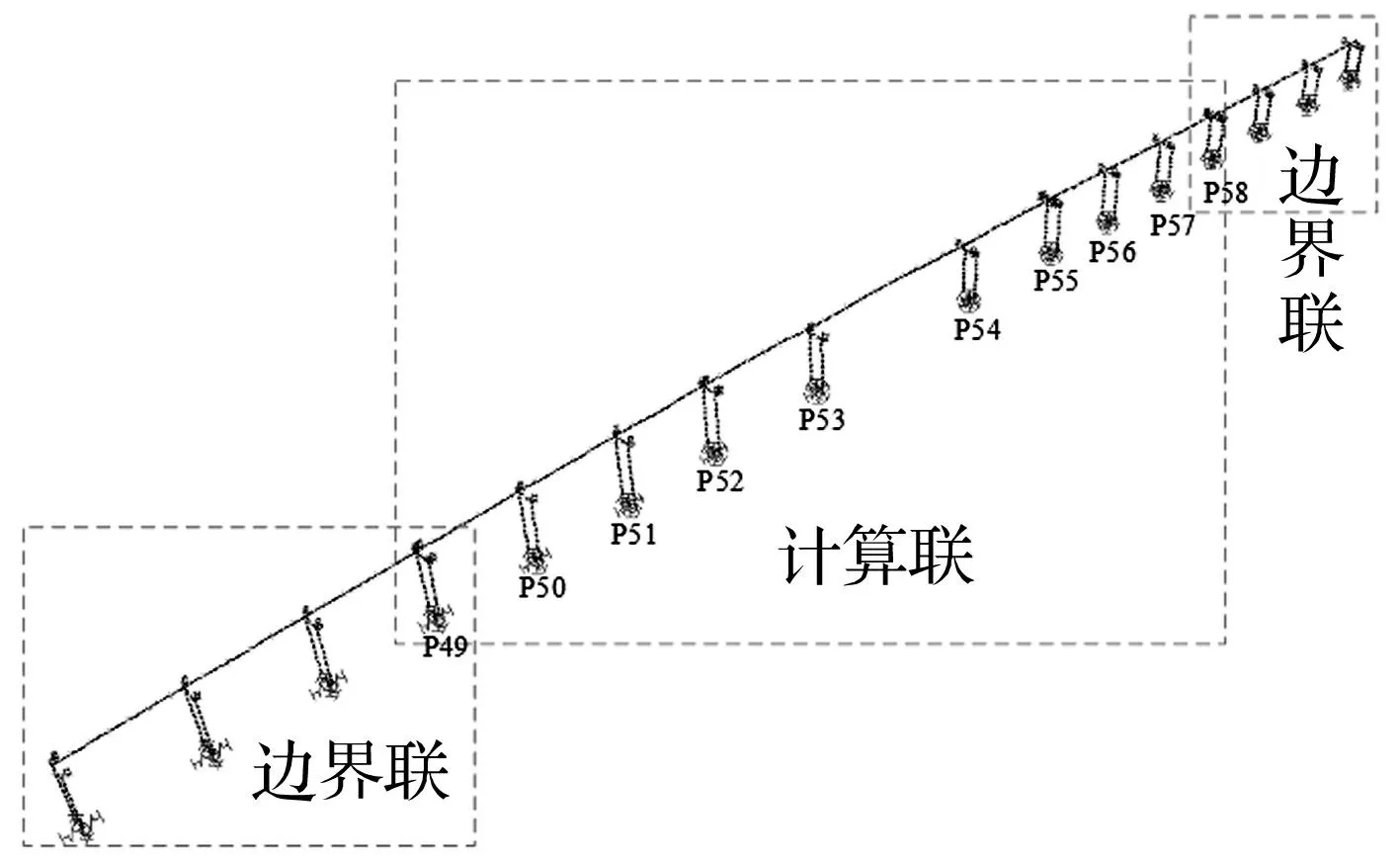
图4　3联主线桥SAP2000模型 Fig.4 SAP2000 model of the multi-span continuous bridge

3计算过程及结果分析

由于采用的5联连续梁桥轴线基本呈直线，墩高变化不大，为等位移准则使用提供了前提。此处，①给出该多联连续梁桥横桥向振型及周期；②验证与控制点相应的模态位移贡献近似等于控制点总位移响应规律；③据所选设计反应谱及3条地震波采用MPA方法、快速MPA方法及非线性动力时程分析方法评估所选连续梁桥抗震性能，并对比分析各种方法计算结果。

3.1横桥向振型及周期

该桥横桥向前6阶振型、周期及位移最大节点见图5。图中，uimax为横桥向第i阶模态位移最大节点。由图5看出，各阶模态位移最大点均在某一联梁梁端。多模态推倒分析中均选各梁端节点为控制点。由于各阶模态周期均大于0.7 s，故等位移准则适用该多联连续梁桥。

图5　前6阶横桥向振型形状 Fig.5 First six transverse modal shapes of the bridge

3.2各阶模态对控制点位移的贡献

由图5知，横桥向各阶模态位移最大点基本均在各联梁梁端，多模态推倒分析时分别选其作为控制点，与各阶模态对应，分别将其称为u1max(第2联右端点)、u2max(第1联右端点)、u3max(第3联右端点)、u4max(第4联右端点)、u5max(第1联左端点)及u6max(第5联右端点)；再增加第二个脚注，uij代表第j阶模态对第i个控制点位移响应的贡献。据MPA方法计算出各阶模态的目标位移，进一步计算出各阶模态对各控制点总位移的贡献(各阶模态位移贡献与SRSS组合后百分比)见表1。由表1看出，控制点位移响应主要由与其对应阶模态控制，模态贡献与总位移响应比值一般均在93%以上(除模态2外，最小时为88.3%)。说明可近似认为控制点位移响应主要来自与其对应阶的模态贡献。反之，即可近似将控制点弹塑性位移响应作为与该控制点相应阶模态的位移贡献，即该阶模态的目标位移。

该现象支持了本文第2部分观点，即可近似将控制点位移总响应作为与各控制点对应阶的模态贡献。即可将5%阻尼比反应谱分析的各控制点位移作为MPA分析中相应模态的目标位移。

3.33种计算方法结果对比分析

以设计E2反应谱作为地震动输入，对该多联连续梁进行反应谱分析获得各控制点目标位移，进行快速MPA分析。以3条人工地震波作为地震动输入，对该多联连续梁桥进行MPA及时程分析，并取3条人工地震波输入下响应最大值。

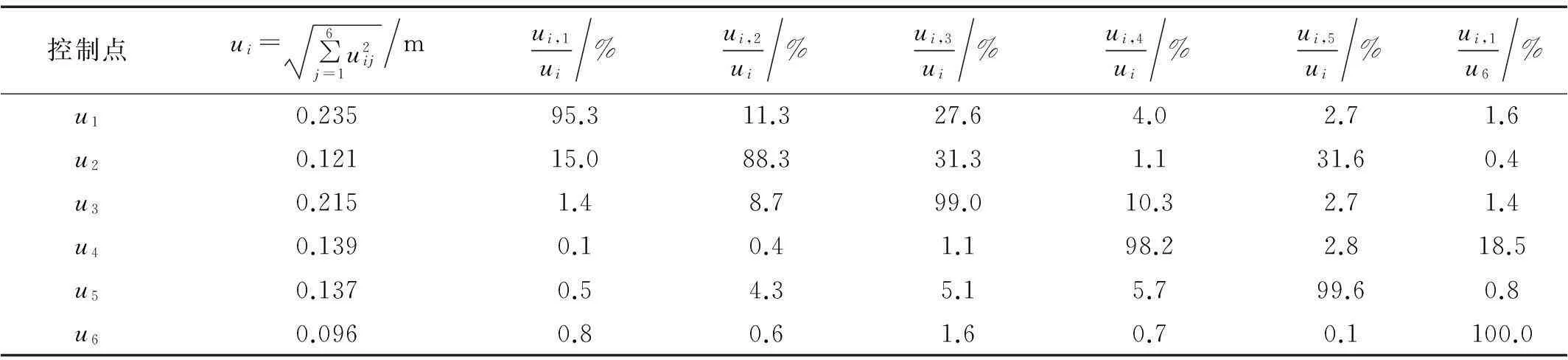
表1　各阶模态对控制点位移贡献

3.3.1墩顶处梁节点位移

3种方法计算所得各墩顶处梁侧向位移见图6。

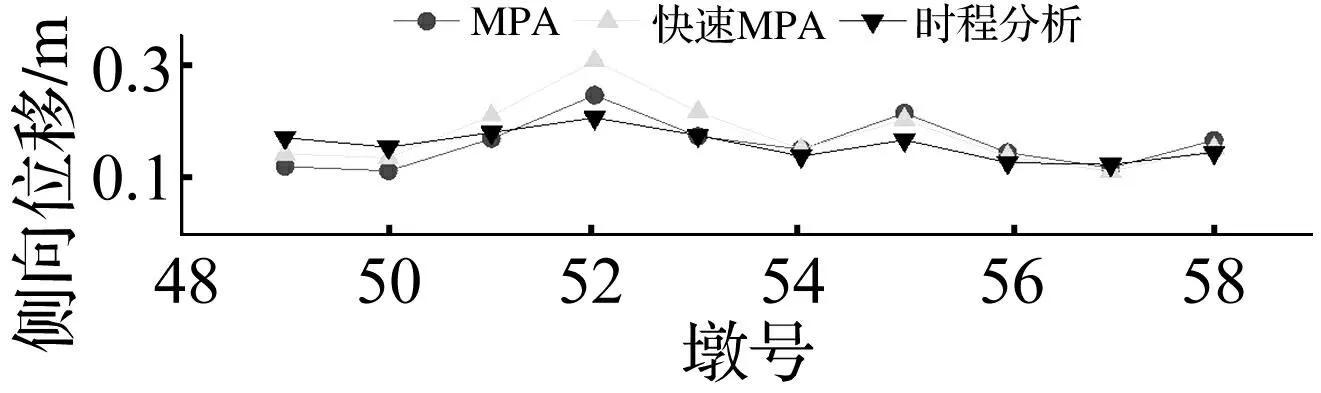
图6　各墩顶处梁侧向位移 Fig.6 Lateral displacements of girder at top of piers

用快速MPA方法计算的梁体位移接近或大于MPA方法，一般大于非线性动力时程分析的梁体位移(P49、P50号墩处快速MPA分析结果略小)。

与非线性动力时程分析结果相比，MPA方法对墩顶位移预测的最大误差为29.7%(P49墩顶)，快速MPA方法对墩顶位移预测最大误差为48.4%(P52墩顶)。因推倒分析时采用固定的侧向力分布模式，不能考虑塑性发展过程中结构刚度矩阵变化，一定程度上夸大过渡墩位移所致。若提高计算精度，考虑推倒分析过程中桥梁结构动力特性变化，则需采用自适应的MPA方法[14]。对整体效果而言，MPA方法可对梁体位移作出较好预测。快速MPA方法误差稍大，较MPA方法计算梁侧移结果保守，可用于梁体侧移快速评估。

3.3.2墩底、系梁端部塑性铰转角

用MPA、快速MPA方法及非线性时程分析方法计算获得各墩底、系梁端部最大塑性铰转角据各纤维截面屈服曲率及各塑性铰相应于屈服曲率的屈服转角见图7、图8。塑性铰转角超过屈服转角横线时表示该处产生塑性铰。

由图7知，与对梁侧移评估精度相比，MPA方法对P49、P50、P52墩底塑性铰转角评估精度较差，均超过30%，而对其它墩底塑性铰转角评估误差则在30%以内。说明MPA方法对结构局部变形评估精度低于对整体变形。快速MPA方法计算的塑性铰转角较MPA结果及误差偏大，P52墩塑性铰转角误差最大为90.4%。虽快速MPA方法误差稍大，但与MPA方法相比结果保守，可用于梁体侧移快速评估。

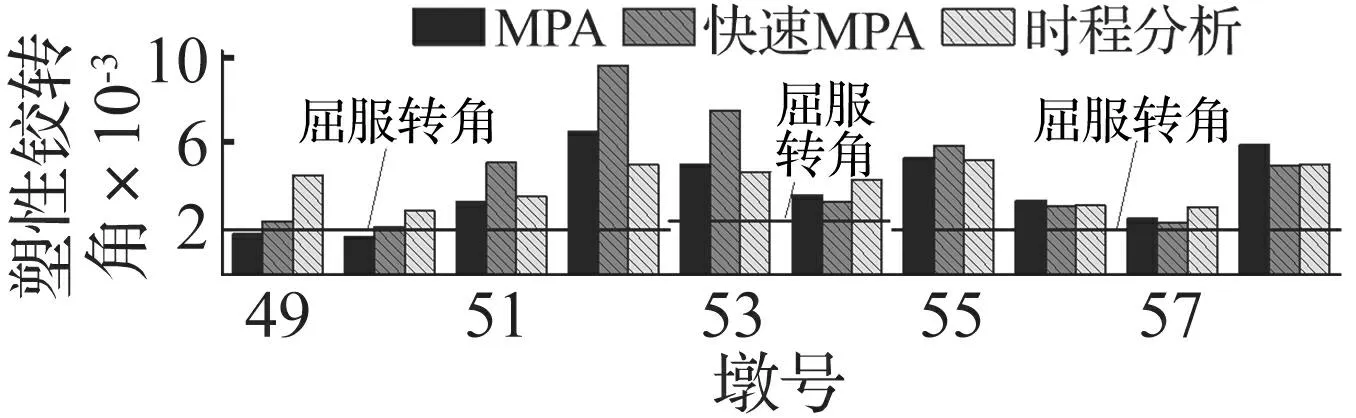
图7　各墩墩底塑性铰转角 Fig.7 Plastic hinge rotations at bottom of piers

由图8知，快速MPA方法对P52、P53墩处横系梁塑性铰转角计算值偏大。两种多模态推倒分析方法(MPA及快速MPA方法)对P49、P50处横系梁塑性铰转角计算值偏小。总体而言，两种推倒分析方法对横系梁塑性铰转角评估结果较好。

图8　各墩系梁最大塑性铰转角 Fig.8 Plastic hinge rotations at ends of strainingbeams

由图7、图8看出，MPA方法未能捕捉到P49、P50墩底塑性铰；快速MPA方法成功捕捉到连续梁桥产生的所有塑性铰。

3.3.3墩底塑性铰区剪力

用MPA、快速MPA方法及非线性时程分析方法计算所得各墩底塑性铰区最大剪力见图9。由图9看出，MPA、快速MPA方法计算所得墩底塑性铰区剪力与非线性动力时程分析结果非常接近，误差在22%以内。MPA方法可有效评估桥梁塑性铰区剪力。减小计算量情况下，快速MPA法对塑性铰区剪力的评估结果与MPA方法计算结果基本一致。

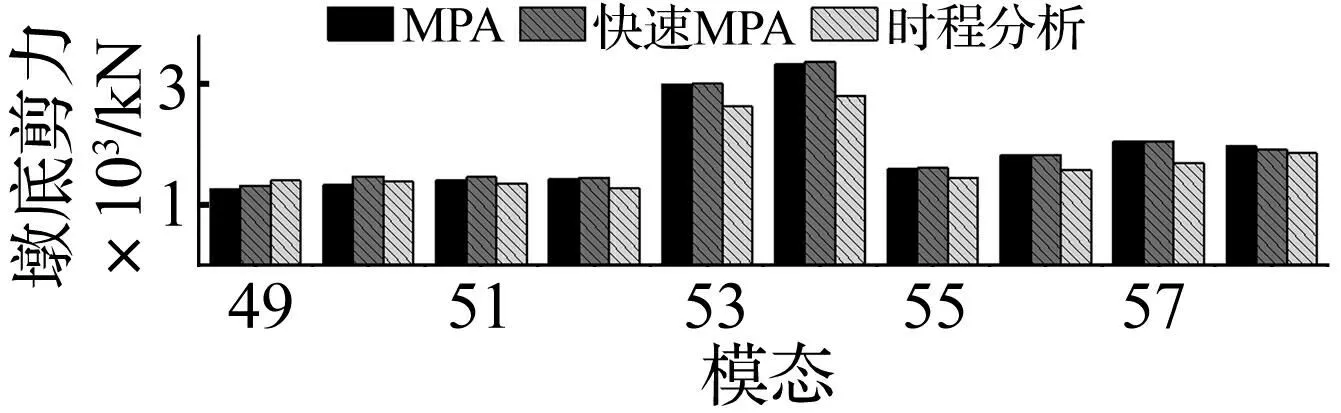
图9　各墩墩底塑性铰区剪力 Fig.9 Shear forces of plastic hinges at bottom of piers

3.3.4各墩承台底弯矩

由于采用六弹簧模型模拟群桩基础，承台底总弯矩大小可代表墩底最不利桩基的地震动响应。用MPA方法、快速MPA方法及非线性时程分析方法计算所得各承台底弯矩见图10。由图10看出，减小计算量情况下基于等位移准则的快速MPA法对承台底弯矩评估结果与MPA方法计算结果基本一致，仅对P54墩承台误差为15.9%，其它墩误差均在15%以内，为有效评估桩基的抗震性能提供有力保证。说明基于等位移准则的MPA可对桩基的抗震性能作出快速有效评估。

图10　各墩承台底弯矩 Fig.10 Moments at bottom of caps

3.3.5不同墩高参数分析

静力弹塑性方法为近似方法，无严密的理论基础。为验证快速MPA方法的适用性，本文在原墩高基础上选整体高度降低5 m、增加5 m、增加10 m的3种新模型进行参数分析。各种墩高下桥梁梁体侧移见图11。由图11看出，随墩高增加P52号墩顶处梁侧移误差有增大趋势(4种情况分别为50%、48%、98%、84%)。此为墩高增加桥墩延性变形增大所致，即大误差因固定侧向力分布模式局限性引起；但对其它墩顶处梁体侧移计算误差均在30%以内。整体而言，快速MPA方法可有效预测不同延性的多联连续梁桥抗震性能。

图11　各墩墩顶处梁侧向位移 Fig.11 Lateral displacements of girder at top of piers

对参数分析引入的3种新模型而言，快速MPA方法对其塑性铰转角、塑性铰区剪力及承台底弯矩评估效果与原模型基本一致，此处不再赘述。

4结论

提出以等位移准则计算多联连续梁桥目标位移，并与MPA方法结合形成快速MPA方法。通过对某3联连续梁桥分析、计算，结论如下：

(1)对等位移准则适用的多联连续梁桥进行多模态推倒分析时，若对各阶模态分别选取位移最大点为控制点，则该点模态位移贡献占控制点弹塑性位移的90%以上，可近似将5%阻尼反应谱分析的控制点位移作为多模态推倒分析的目标位移。

(2)快速MPA分析结果较MPA分析及时程分析结果稍大，但计算结果较保守，可作为初步设计阶段抗震依据，且适用不同墩高桥梁。

(3)快速MPA方法大大简化多联连续梁桥多模态推倒分析步骤，用SAP2000即可实施，易于掌握，可作为初设阶段多联连续梁桥抗震性能评估工具。

参考文献

[1]Chopra A K,Goel R K. A modal pushover analysis procedure for estimating seismic demands for buildings[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3): 561-582.

[2]Kappos A J,Paraskeva T S,extos A G. Seismic assessment of a major bridge using modal pushover analysis and dynamic time-history analysis[J]. Keynote lecture, ICCES, 2004, 4: 673-680.

[3]Paraskeva T S,Kappos A J,extos A G. Extension of modal pushover analysis to seismic assessment of bridges[J]. Earthquake Engineering & Structural Dynamics, 2006,35(10): 1269-1293.

[4]Paraskeva T S,Kappos A J. Further development of a multimodal pushover analysis procedure for seismic assessment of bridges[J]. Earthquake Engineering & Structural Dynamics, 2010, 39(2): 211-222.

[5]魏标,李建中. 非规则梁桥的模态推倒分析[J]. 振动与冲击, 2011, 30(2): 110-114.

WEI Biao, LI Jian-zhong.Modal pushover analysis of an irregular continuous bridge[J]. Journal of Vibration and Shock,2011, 30 (2): 110-114.

[6]魏标,李建中. 基于位移的非规则梁桥抗震设计[J]. 土木工程学报, 2011, 44(8): 95-101.

WEI Biao, LI Jian-zhong. Displacement-based seismic design of irregular continuous bridges[J]. China Civil Engineering Journal. 2011, 44 (8): 95-101.

[7]陈星烨,唐雪松,赵冰. 修改的 MPA 法用于连续刚构桥的抗震性能分析[J]. 振动与冲击, 2010, 29(12): 93-96.

CHEN Xing-hua,TANG Xue-song, ZHAO Bing. Modified MPA for seismic performance evaluation of continuous rigid frame bridges[J]. Journal of Vibration and Shock,2010,29(12): 93-96.

[8]Caltrans S D C. Caltrans seismic design criteria version 1.3[S]. California Department of Transportation, Sacramento, California, 2004.

[9]郭磊. 桥梁结构基于位移的抗震设计方法研究[D]. 上海: 同济大学, 2006.

[10]魏标,李建中. 连续梁桥横桥向等位移准则[J]. 振动与冲击, 2009, 28(11): 100-104.

WEI Biao, LI Jian-zhong. Equal displacement rule in transverse direction of multi-span continuous bridge[J]. Journal of Vibration and Shock,2009, 28 (11):100-104.

[11]Priestley M J N. Seismic design and retrofit of bridges[M].John Wiley & Sons, 1996.

[12]CJJ 166-2011,城市桥梁抗震设计规范[S].

[13]Pinho R, Monteiro R, Casarotti C, et al. Assessment of continuous span bridges through nonlinear static procedures [J]. Earthquake Spectra, 2009, 25(1): 143-159.

[14]Shakeri K, Tarbali K，Mohebbi M. Modified adaptive modal combination procedure for nonlinear static analysis of bridges[J]. Journal of Earthquake Engineering, 2013, 17(6): 918-935.