饱和土体中多排柱腔屏障对压缩快波隔离

第一作者徐平男，博士，副教授，1977年2月生

饱和土体中多排柱腔屏障对压缩快波隔离

徐平1，铁瑛2，陈斌3

(1. 郑州大学水利与环境学院，郑州450001；2. 郑州大学机械工程学院，郑州450001；3.宁波市轨道交通工程建设指挥部, 浙江宁波315012)

摘要：假定柱腔(圆柱形空腔)长度远大于直径，将多排柱腔组成的非连续屏障对平面P1波(压缩快波)隔离简化成弹性波多重散射的二维平面问题，利用复变函数保角映射法及波场势函数展开法，据柱腔自由(土骨架轴向、切向应力为零)边界条件获得散射波场势函数展开式的待定复系数理论解。通过分析位移比值(屏障后某点由入射、散射弹性波产生的总位移与入射弹性波单独产生的位移之比)变化规律，对比单、双及三排柱腔屏障的隔离效果。研究表明，边界不透水柱腔屏障隔离效果好于透水；多排柱腔屏障对高频入射P1波隔离效果好于低频入射；随排数增多柱腔屏障隔离效果明显提高，有效隔离区域明显增大；当排数达到三排时柱腔屏障后一定范围内隔离效果达70%，效果较理想。

关键词：饱和土体；多排柱腔；非连续屏障；隔离效果；隔振设计

基金项目：国家自然科学

收稿日期：2014-02-26修改稿收到日期：2014-08-19

中图分类号:TU435文献标志码：A

Isolation of fast longitudinal waves by barriers composed of several rows of cylindrical cavities in saturated soils

XUPing1,TIEYing2,CHENBin3(1. School of Water and Environment, Zhengzhou University, Zhengzhou 450001, China;2.School of Mechanical Engineering, Zhengzhou University, Zhengzhou 450001, China;3.Ningbo Urban Rail Transit Project Construction Headquarters, Ningbo 315012, China)

Abstract:The lengths of cylindrical cavities were considered as much larger than their diameters, so the isolation of incident plane P1 waves (fast compressive wave) by discontinuous barriers composed of several rows of cylindrical cavities was simplified as a two-dimensional plane problem. The conformal mapping method of complex functions and expansion method of wave functions were adopted, the cylindrical cavities were considered to be of free boundaries, where no stresses exist, and then the theoretical solutions about the complex coefficients of scattering wave potential functions were obtained. By studying the normalized displacement amplitudes, which are expressed as the ratios of displacement amplitudes of soils behind the barriers caused by both the incident and scattering waves to those only by the incident P1 waves, the isolation effects of the barriers composed of one, two and three rows of cylindrical cavities were compared. The results reveal that the isolation effects of barriers composed of several waterproof cylindrical cavities are better than those composed of permeable cylindrical cavities; the isolation effects of barriers composed of several rows of cylindrical cavities on incident P1 waves with higher frequencies are much better than on those with lower frequencies; with the increasing of row number of cylindrical cavities, the vibration isolation effects is obviously improved, and the effective isolation area is obviously increased; as the row number of cylindrical cavities reaches three, the isolation effects at some locations behind the barriers are much better and almost increase to 70%.

Key words:saturated soil; several rows of cylindrical cavities; discontinuous barrier; isolation effect; vibration isolation design

非连续屏障由多个不连续个体(如桩、柱腔)组成，尽管对振动波隔离效果略低于空沟，但施工方便、维护费用低，较空沟应用前景更广。大多采用理论分析及数值模拟等方法研究非连续屏障，Avilés等[1-2]首次用波动理论获得均质土体中单排桩对S波隔离的精确解；Kattis等[3-4]通过频域边界元技术建立三维单排圆桩、方桩隔振问题模型研究表明，桩间距为影响隔振效果的决定性因素。李志毅等[5]以瑞利波散射积分方程为基础，研究多排桩屏障对瑞利波的三维隔离问题，认为多排桩屏障体系隔振效果主要取决于桩的排数，而排距对隔振效果影响较小。时刚等[6]通过推导单排桩屏障对瑞利波散射的三维边界元方程，认为增加单排桩长度、提高桩身剪切模量均能有效提高隔振效果；高广运等[7]利用迭代法对瑞利波散射积分方程精确求解，分析弹性土体中多排桩对瑞利波隔离。陆建飞等[8]用数值方法模拟多排桩对高速列车振动隔离表明，小间距、大桩长多排桩屏障隔离效果最好。徐平[9]用保角映射法及波场位移势函数展开法对多排空心管桩屏障对平面SV波隔离问题进行理论求解及数值计算，并分析管桩壁厚、排数对隔离效果影响。李校兵等[10]利用一组可求解多散射问题的圆柱坐标系统及界面处位移连续条件，建立饱和土体中单排柱腔对压缩快波的理论解答，认为饱和土的渗透性对隔离效果影响较明显。天然土体为由固、液、气三相介质组成的集合体，若孔隙被流体(通常意义的水)充满则为饱和土，故需研究饱和土体中非连续屏障隔振效果，但关于饱和土体中多排柱腔组成的非连续屏障隔振效果研究尚少见。

不同于一般弹性介质，饱和土体中可传播一种剪切波(S波)与两种压缩波，即快压缩(P1)波与慢压缩(P2) 波[11]。本文用复变函数的保角映射法及波函数展开法，获得多排柱腔屏障对平面弹性波隔离问题的理论解，并对比单、双、三排柱腔屏障隔离效果。

1饱和土体中多排柱腔波场展开

1.1饱和土体中波场理论

据Biot波动理论[11]，饱和土体基本控制方程为

土体应力-应变关系

σij=λui,iδij+2μεij-αpfδij

(1)

渗流连续性方程

-pf=Mwi,i+αMui,i

(2)

土体运动方程(不计体力)

(3)

流体运动方程

(4)

式中：pf为孔隙流体压力；λ，μ为固相土骨架Lamé弹性常量；u为固相土骨架位移；w为孔隙流体相对土骨架位移；M，α分别为表征土颗粒、孔隙流体压缩性常数；δij为Kronecker Delta符号；ρ=fρf+(1-f)ρs为饱和土体总密度，ρs为土颗粒密度，ρf为孔隙流体密度，f为饱和土体孔隙率；m=ρf/f；b=η/kd，η，kd分别为孔隙流体粘滞、渗透系数。

将式(1)、(2)代入式(3)、式(2)代入式(4)，整理可得饱和土体波动问题矢量方程为

(5)

式中：λc=λ+α2M；u，w为位移矢量。

引入标量势φ，φ及矢量势ψ，χ表示土骨架与孔隙流体中波函数，则波场可分解为

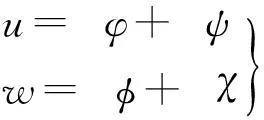
(6)

将式(6)代入式(5)，得饱和土体的波动方程为

(7)

式中：ω为入射频率；Q=mω2+iωb。

经求解可得饱和土体中P1波、P2波及S波波数k1，k2，ks计算公式为

(8)

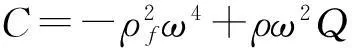
用势函数φ1，φ2，ψ分别表示土骨架中P1、P2、S波波场，φ1，φ2，χ分别表示孔隙流体中P1、P2、S波波场，据式(7)、(8)可得势函数φ1，φ2，χ与φ1，φ2，ψ之间转换关系式为

φ1=γ1φ1,φ2=γ2φ2,χ=γsψ

(9)

式中：γ1，γ2，γs表达式为

(10)

1.2入射波场势函数展开

饱和土体中P2波衰减较快，且占总弹性波能量比例较小，因此对爆炸、交通、重工业厂房等常见振动问题，通常不考虑入射P2波。入射P1及S波会产生耦合散射，即饱和土体散射波中同时含P1、P2、S波成分，因此P1波与S波求解过程完全相似，限于篇幅，本文仅对入射P1波解答。

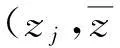
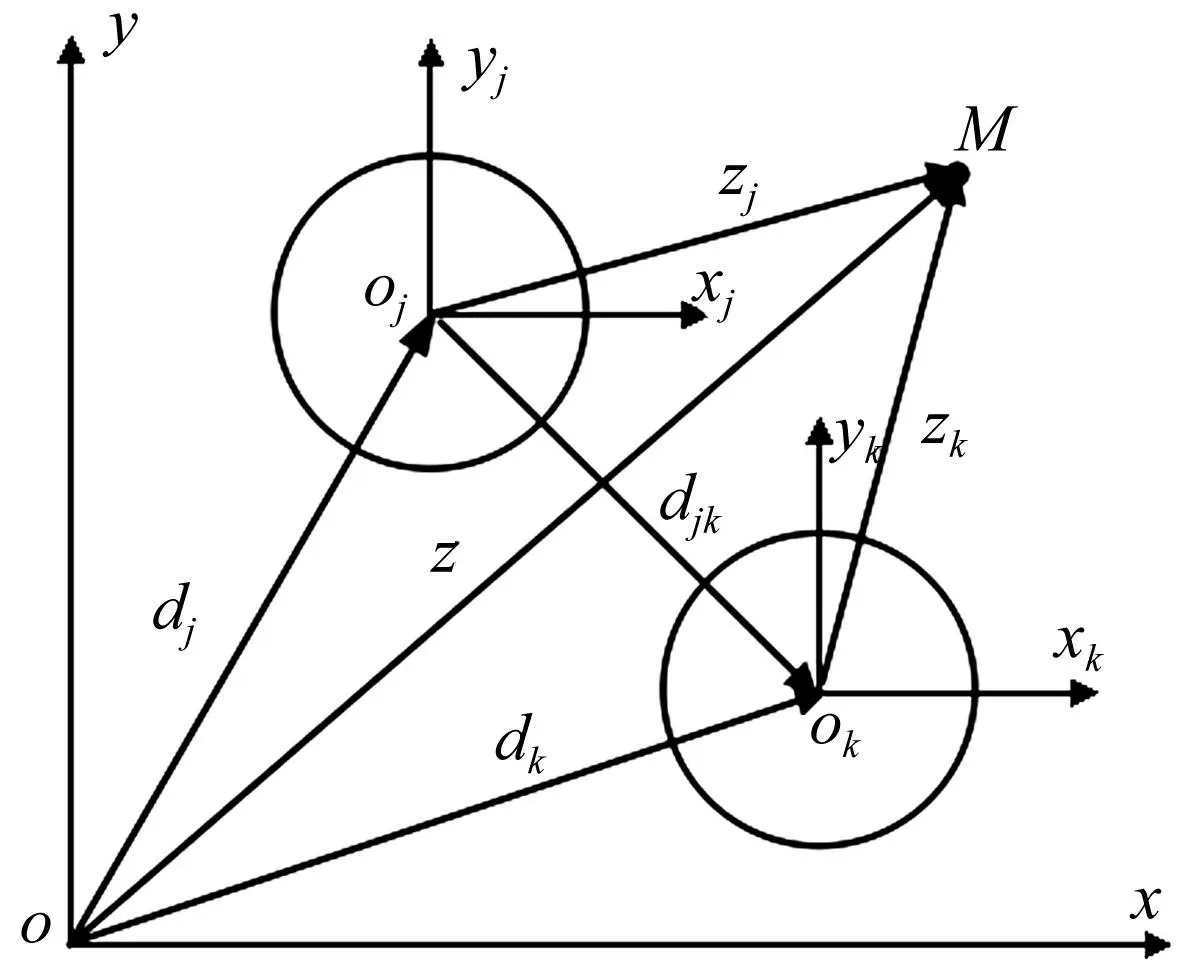
图1　柱腔分布及坐标系设置 Fig.1 Distribution of cylindrical cavities and coordinate systems

取入射平面P1波幅值为φ0，在参考直角坐标系(x,y)下，饱和土体土骨架中入射平面P1波势函数为

φinc=φ0exp[ik1(xcosβ+ysinβ)]

(11)

式中：上标inc表示入射；β为入射P1波与水平方向(即x轴)夹角。

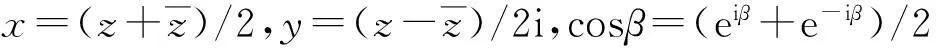
(12)

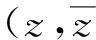
(13)

1.3散射波场势函数展开

(14)

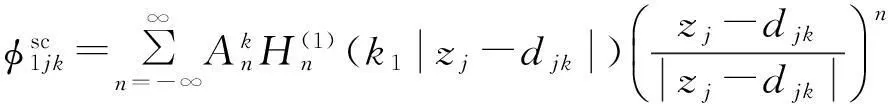
(15)

通过叠加，观测点M处饱和土体土骨架中总散射P1波的势函数展开式及M处总散射S波势函数为

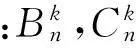
2待定复系数求解

引入保角变换zj=rjexp(iθj)，由弹性介质中应力、位移极坐标表达式[12]，得饱和土体中应力、位移极坐标表达式为

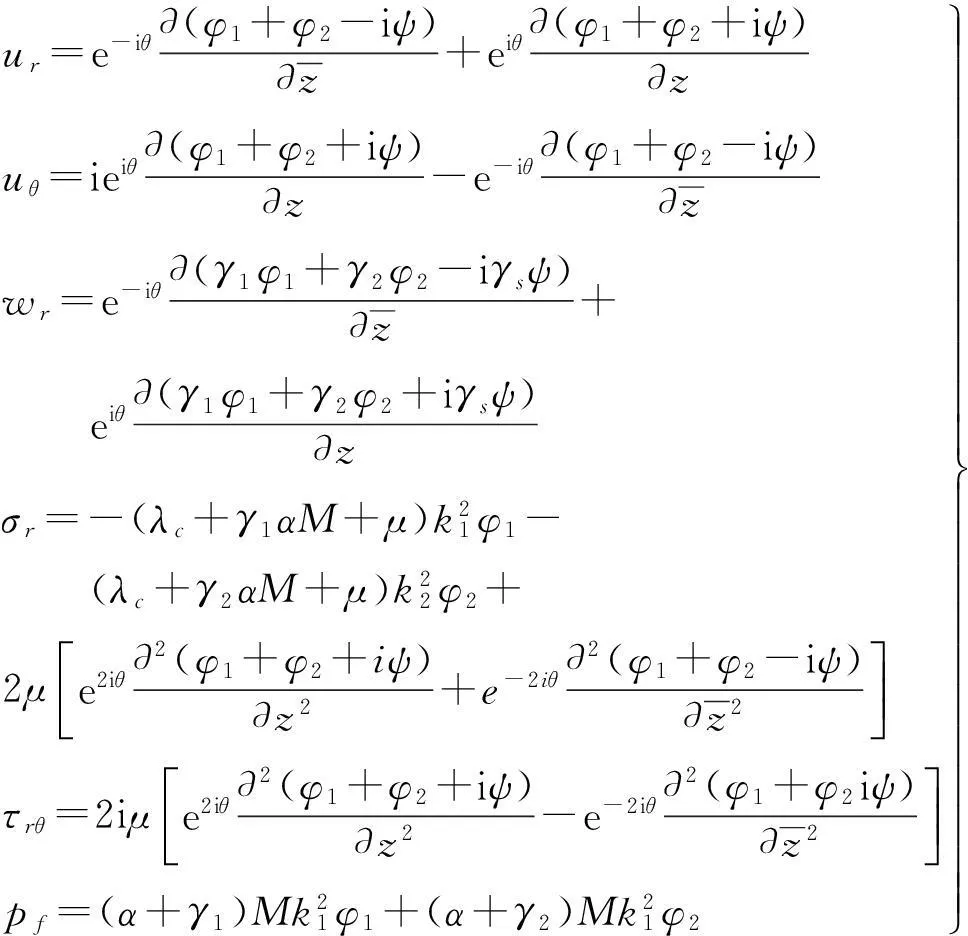
设饱和土体在柱腔边界处(rj=aj)自由，边界分不透水(柱腔建成后立即插入PVC管材，阻断水渗透)、透水(柱腔建成后保持土体原有渗透性)两种，即

(18)

(19)

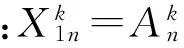
边界不透水为

边界透水为

(20)

(21)

由于式(21)为Fourier-Bessel函数的无穷级数解，n的取值为-∞～∞，实际计算时无法实现，更无必要，只需将n截取到N，保证N已对应力、位移不再产生明显影响即可，由文献[14]，规定本文计算的容许误差为0.005%。

3隔离效果分析

为简化算例计算，取所有柱腔半径a相同，且均匀布置，设入射波垂直屏障入射，即β=π/2。为分析屏障隔离效果引入位移比值(屏障后某点由入射P1波与散射P1波、P2波、S波产生的位移之和vy与未设屏障时由入射P1波单独产生的位移v0比值)|vy/v0|，该比值越小，说明屏障隔离效果越好。由文献[13]取饱和土体物理力学参数见表1。

表1　饱和土体的物理力学参数

由文献[1-2]知，d/a=3.0时单排桩屏障的隔离效果最佳，故本文取柱腔间距d/a=3.0，柱腔按正三角形布置，见图2。计算时单排柱腔N=8，双排柱腔N=17，三排柱腔N=25。

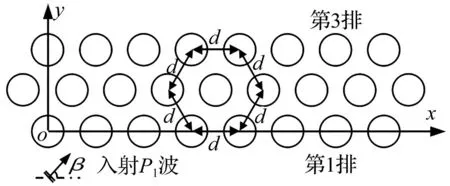
图2　多排柱腔布置 Fig.2 Arrangement of several rows of cylindrical cavities

3.1计算结果正确性验证

与文献[10]对比分析，取单排柱腔屏障(N=8、d/a=3.0)，绘制屏障中心线(x/a=10.5)|vy/v0|沿y/a的变化曲线，见图3。由图3看出，本文与文献[10]结果相同，从而验证本文理论解答与计算程序(Matlab软件编制)的正确性。

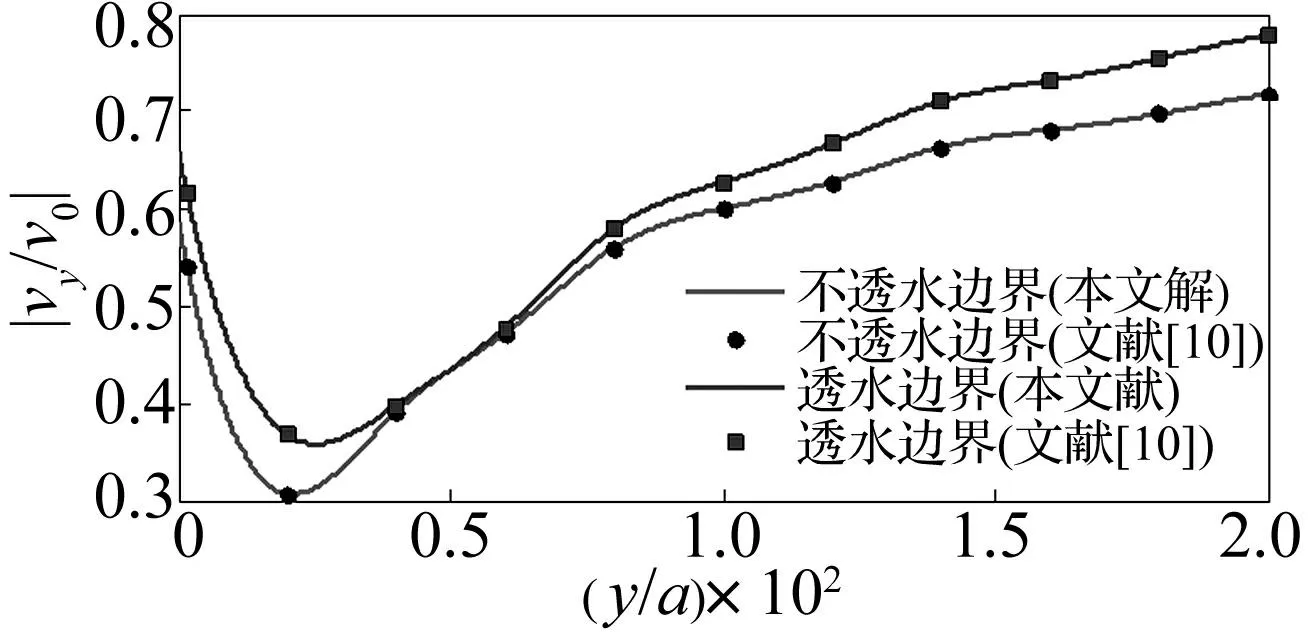
图3　单排柱腔屏障中心线|v y/v 0|沿y/a变化曲线 Fig.3 Curves of|v y/v 0|changing with y/a at the center of one row of cylindrical cavities

3.2柱腔排数及边界透水对隔离效果影响

取入射P1波无量纲频率Re(k1a)=0.2(低频)，绘制单、双、三排柱腔屏障后一定区域内(0≤x/a≤21, 0≤y/a≤300)的|vy/v0|等值线，见图4～图6。比较图4～图6看出，①对相同柱腔屏障，不透水边界的柱腔屏障隔离效果好于透水边界，因不透水边界，孔隙流体相对土骨架位移wr在柱腔边界上为零，孔隙流体位移不能继续传递，屏障后位移有所减小，即不透水边界更能有效耗散振动波能量。②随柱腔排数增多，屏障隔离效果明显提高，有效隔离区域明显扩大，达到三排时屏障后一定区域内(不透水边界y/a≤110、透水边界y/a≤90)|vy/v0|≤0.3，即隔离效果超过70%，较理想。

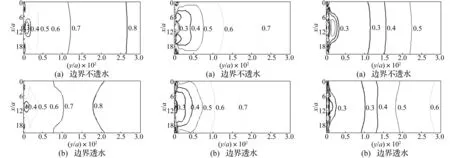
图4 单排8个柱腔后位移比值vy/v0等值线(低频)Fig.4Contoursofvy/v0behindarowof8cylindricalcavitiesforincidentP1waveswithlowfrequencies图5 双排17个柱腔后vy/v0的等值线(低频)Fig.5Contoursofvy/v0behindtworowsof17cylindricalcavitiesforincidentP1waveswithlowfrequencies图6 三排25个柱腔后vy/v0的等值线(低频)Fig.6Contoursofvy/v0behindthreerowsof25cylindricalcavitiesforincidentP1waveswithlowfrequencies

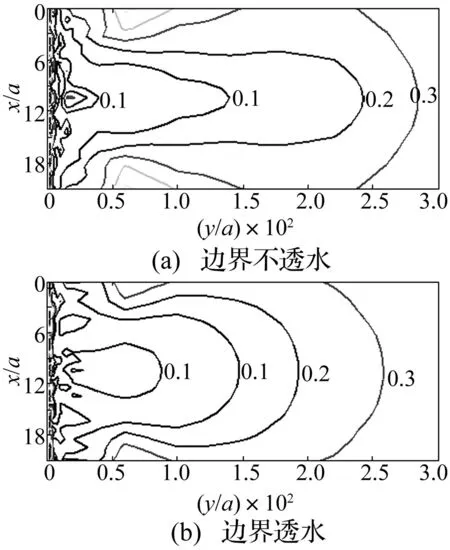
图7　三排25个柱腔后|v y/v 0|等值线(高频) Fig.7 Contours of |v y/v 0|behind three rows of 25 cylindrical cavities for incident P 1 waves with high frequencies

3.3入射频率对隔离效果影响

取入射P1波无量纲频率Re(k1a)=1.0(高频)，绘制三排柱腔屏障后一定区域内(0≤x/a≤21, 0≤y/a≤300)的|vy/v0|等值线，见图7。

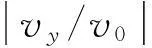
4结论

用复变函数保角映射法与波场势函数展开法获得饱和土体中多排柱腔屏障对各种平面P1波隔离问题的理论解。通过数值计算，结论如下：

(1)边界不透水时，柱腔屏障隔离效果好于透水；柱腔屏障对高频入射P1波隔离效果好于低频；屏障后一定区域内隔离效果超过70%，较理想。

(2)柱腔排数达到三排时屏障后y/a≤100长度范围内隔离效果达到或超过70%，隔振效果较理想。

参考文献

[1]Avilés J, Sánchez-Sesma F J. Piles as barriers for elastic waves[J]. Journal of Geotechnical Engineering, 1983,109(9): 1133-1146.

[2]Avilés J, Sánchez-Sesma F J. Foundation isolation from vibrations using piles as barriers[J]. Journal of Engineering Mechanics, 1988, 114(11): 1854-1870.

[3]Kattis S E, Polyzos D, Beskos D E. Modelling of pile wave barriers by effective trenches and their screening effectiveness [J]. Soil Dynamics and Earthquake Engineering,1999,18(1): 1-10.

[4]Kattis S E, Polyzos D, Beskos D E. Vibration isolation by a row of piles using a 3-D frequency domain BEM[J]. International Journal for Numerical Methods in Engineering, 1999, 46(5): 713-728.

[5]李志毅,高广运,邱畅,等. 多排桩屏障远场被动隔振分析[J]. 岩石力学与工程学报, 2005, 24(21): 3990-3995.

LI Zhi-yi, GAO Guang-yun, QIU Chang, et al. Analysis of multi-row of piles as barriers for isolating vibration in far field[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(21): 3990-3995.

[6]时刚,高广运. 饱和地基中单排桩远场被动隔振研究[J]. 振动工程学报,2010, 23(5): 546-553.

SHI Gang, GAO Guang-yun. Three-dimensional analysis of a row of piles as passive barriers in saturated soil[J]. Journal of Vibration Engineering, 2010, 23(5): 546-553.

[7]Gao G Y, Li Z Y,Yue Z Q. Three-dimensional analysis of rows of piles as passive barriers for ground vibration isolation[J]. Soil Dynamics and Earthquake Engineering, 2006,26(11): 1015-1027.

[8]Lu J F, Xu B,Wang J H. A numerical model for the isolation of moving-load induced vibrations by pile rows embedded in layered porous media[J]. International Journal of Solids and Structures, 2009, 46(21): 3771-3781.

[9]徐平. 多排弹性空心管桩屏障对平面SV 波的隔离[J]. 岩土工程学报, 2011, 33(3): 392-397.

XU Ping. Rows of elastic hollow pipe piles as isolation barriers for plane SV waves[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 392-397.

[10]李校兵,戴鹏燕. 饱和土中孔列对平面快纵波的隔离效应[J]. 地震工程与工程振动, 2011, 31(2): 25-30.

LI Xiao-bing, DAI Peng-yan. Isolation effect of cavity array in saturated soils on plane fast longitudinal waves[J]. Journal of Earthquake Engineering and Engineering Vibration, 2011, 31(2): 25-30.

[11]Biot M A. Mechanics of propagation of elastic waves in a fluid-saturated porous solid[J]. Acoust Soc America, 1956, 28(2): 168-191.

[12]Liu D K, Gai B Z, Tao G Y. Applications of the method of complex function to dynamic stress concentration[J]. Wave Motion, 1982 (4): 293-304.

[13]吴世明. 土介质中的波[M].北京:科学出版社,1997: 80-84.

[14]Davis C A, Lee V W, Bardet J P. Transverse response of underground cavities and pipes to incident SV waves[J]. Earthquake Engineering and Structural Dynamics, 2001, 30: 383-410.