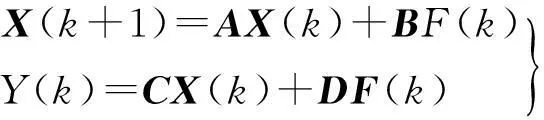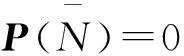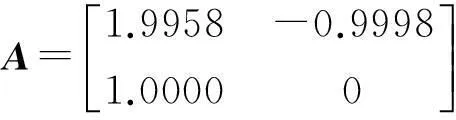变分数阶振子振动控制方法研究

第一作者叶宇旻女，硕士，工程师，1983年9月生

变分数阶振子振动控制方法研究

叶宇旻1,周林根2,谢兴博3

(1.中交第三航务工程勘察设计院有限公司，上海200032；2.上海东华建设管理有限公司，上海200032;3.中国人民解放军理工大学野战工程学院，南京210007)

摘要：针对含变分数阶的无量纲振子振动方程，考虑变分数阶微分算子表达式的复杂性，直接进行控制器设计不现实。通过分析位移时程曲线，采用截断变分数阶微分算子方式获得较好拟合效果。提出变遗忘因子概念，使变分数阶算子变为有限阶次，用其进行控制器设计成为可能，并仿真实例验证该方法的有效性。

关键词：变分数阶；振动控制；变遗忘因子；截断模态

基金项目：国家自然科学基金重点项目(U1134207)； 国家自然科学基金(51178160)

收稿日期：2014-05-14修改稿收到日期：2014-07-23

中图分类号:TU311.3文献标志码：A

Active vibration control method for variable order oscillator

YEYu-min1,ZHOULin-gen2,XIEXing-bo3(1.CCCC Three Harbor Consultants Co. Ltd, Shanghai 200032, China；2. Shanghai Dong Hua Construction Management Co. Ltd, Shanghai 200032, China;3. College of Field Engineering, PLA University?of Science & Technology, Nanjing 210007, China)

Abstract:The dimensionless version of a model oscillator was studied, whose equation of motion is given. Due to the complication of the approximate expression of variable order(VO) differential operator, it is difficult to design directly the controller. Based on the analysis of the curve of displacement versus time, a truncation mode of VO differential operator was proposed. The concept of variable oblivion factor was introduced, meanwhile, an optimal controller was developed for the VO differential equation under study in order to reduce the dynamic responses.

Key words:VO; vibration control; variable oblivion factor; truncation mode

近年来有关分数阶的研究日益增加，在流体力学、固体力学、流变、电磁、电化学、生物学等领域已证明分数阶能更好反映系统的物理特性[1]。将分数阶用于振动控制已显出较好的控制效果[2]，如PID控制[3]等，但分数阶求解较困难，即使周期荷载作用也不存在周期解[4]。目前研究多为常分数阶，即阶次为常数。当阶次为函数表达式时则成为变分数阶，更能反映系统的物理特性。变分数阶概念由Coimbra等[5-6]提出，计算多采用滤波器近似处理。针对变分数阶定义式，Chan等[7]比较FIR与IIR滤波器认为，分别需427及305项方可获得较好计算精度。由此可见计算的复杂性。

振动控制常用黏弹性阻尼器，其阶次函数主要有3种函数[8]，即x，1+x，(1+x2)/2。Balachandran等[9]基于Banach空间探讨其可控性。Diaz等[10]提出忽略微分算子的最优控制策略。Piotr等[11]为避开变阶次项，提出无差拍控制策略。由于变分数阶微分算子表达式含无穷项，直接进行控制器设计不可能。本文以文献[8]的黏弹性振子系统为研究对象，对以上3种阶次函数进行仿真发现，变分数阶表达式主要成分为近计算点的微分算子，可采用有限项近似处理，进行控制器设计。其中，只有阶次函数为(1+x2)/2时项数偏少，适合控制器设计。此类可模拟摩擦阻尼情况(本文研究的主要内容)，其它两类近似项偏多，若用较少项数进行控制器设计，效果不理想。

1模型描述

无量纲变黏弹性振子系统为

D2x(t)+c0Dq(x)x(t)+k0D0x(t)=F(t)

(1)

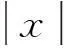
初始条件为

x(0)=0，D1x(0)=0

(2)

对不同黏弹性材料，变阶次函数q(x)表达式不同，即x，1+x，(1+x2)/2。当q(x)=(1+x2)/2时可描述摩擦阻力，此时式(1)可改写为

D2x(t)+c0D(1+x2)/2x(t)+k0D0x(t)=F(t)

(3)

式(3) 可用离散方式求解，简记q(x)为q，有

(4)

(5)

振子离散方程为

xn+2=(Δt)2[F(tn)-

c0Dqxn-k0xn]+2xn+1-xn

(6)

2变分数阶截断模态

在时间间隔[0,tn]内，令h=tn/N，则[tn=nh,n=0,1,…,N]。基于二阶Runge-Kutta法可得Euler预测-校正公式为

(7)

通过仿真发现，当频率处于0～1 300 Hz内时，若阻尼较小位移时程曲线呈现经一段时间波动后位移峰值近似平稳特点；若阻尼较大会很快衰减为零，此时无需振动控制。分析式(4)发现，随时间推移计算项数逐渐增加，为减少计算量借鉴遗忘因子概念，提出变遗忘因子概念，即遗忘因子为变量。截断算法可表示为

(8)

式中：n1为遗忘因子，只保留与当前计算时刻前n1步，即n-n1=const。

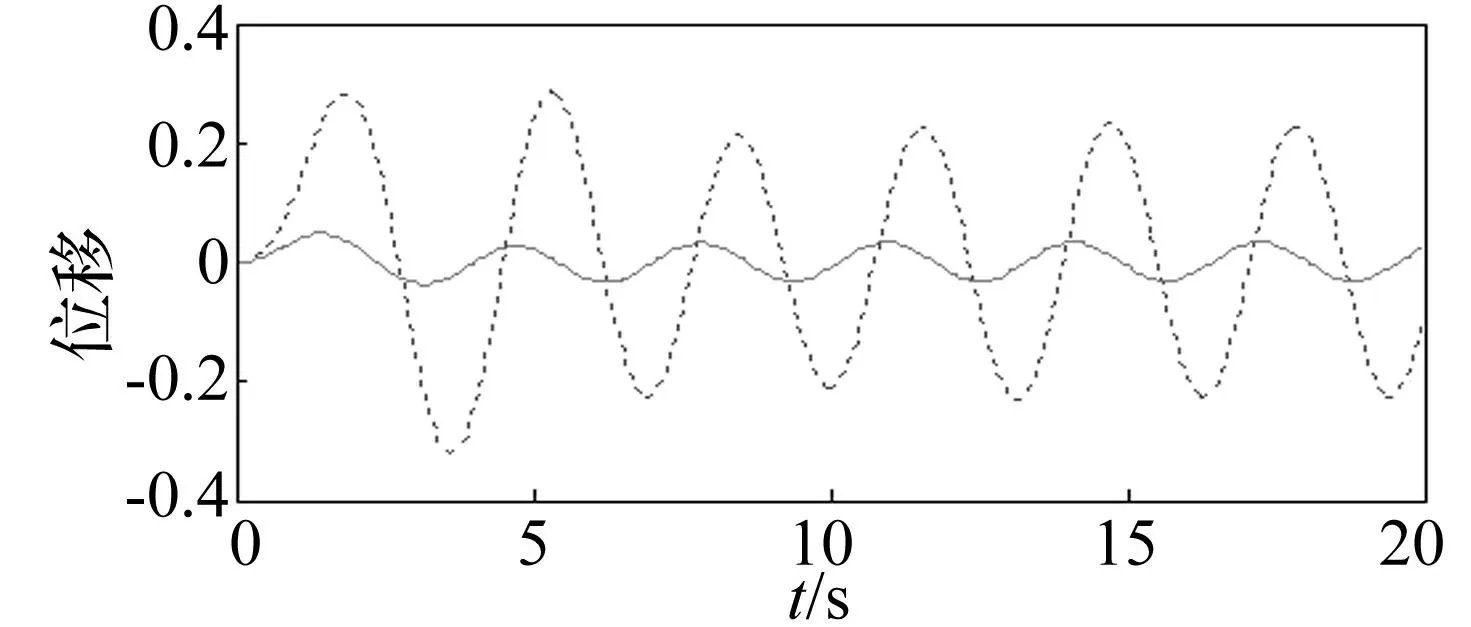
考虑高阻尼系统无需进行控制器设计，故以小阻尼为例，令c0=0.3，k0=1，F(t)=0.5sin(2t)，取N=200，仿真结果见图1实线；若以式(8)计算，取n-n1=30，仿真结果见图1虚线。由图1看出，5 s后仿真逼近效果较好。

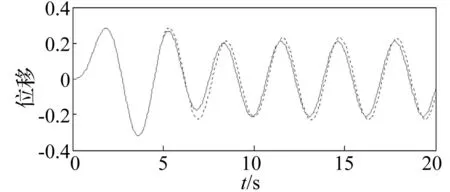
图1　完整及截断模态位移时程曲线 Fig.1 The history curve of displacement versus time of the whole and oblivion modes

3振子控制策略

利用向前差分公式，一阶导数可写为

(9)

将式(9)代入式(8)，得

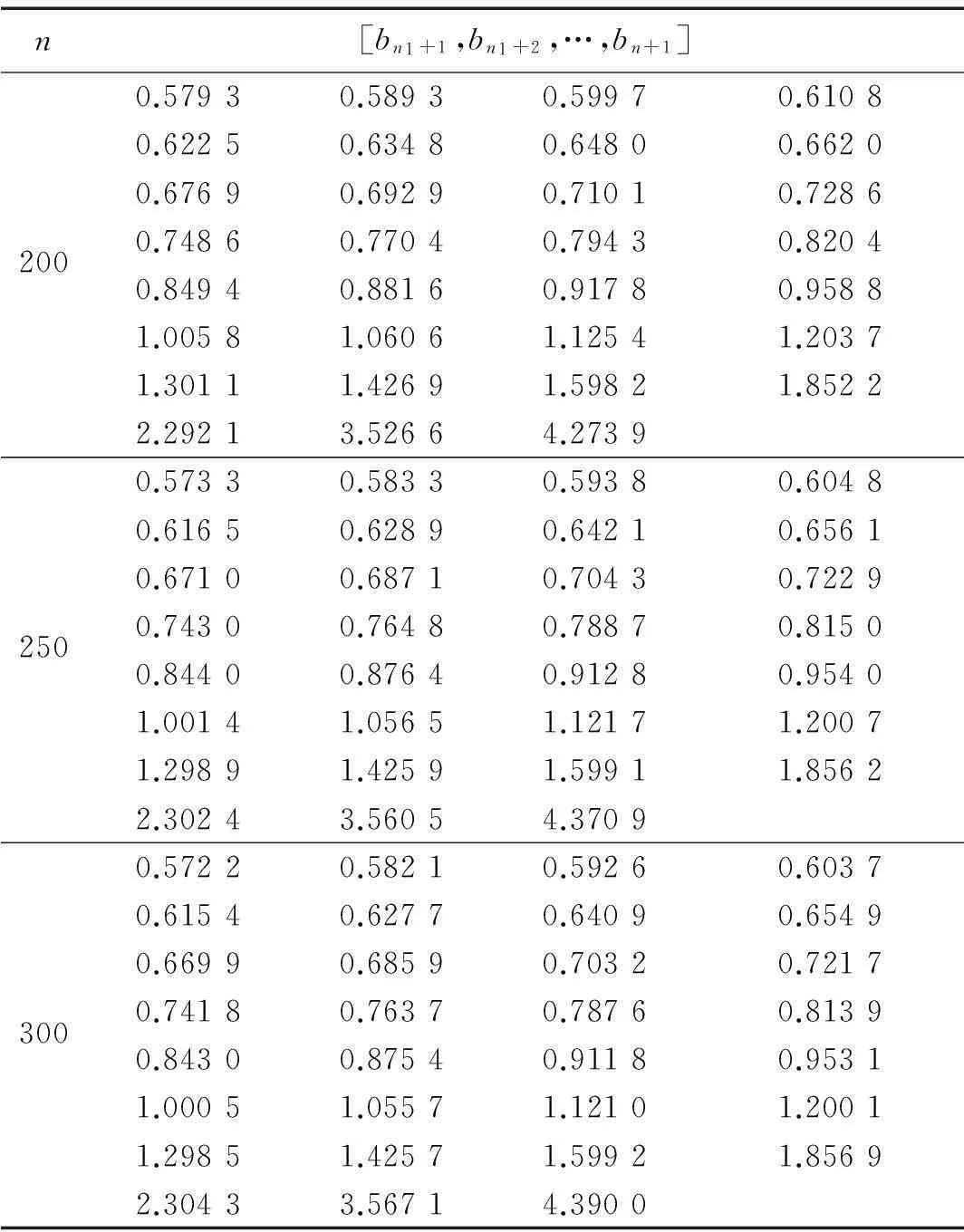
Dqxn≈bn+1xn+1+bnxn+…+bn1+1 xn1+1

(10)

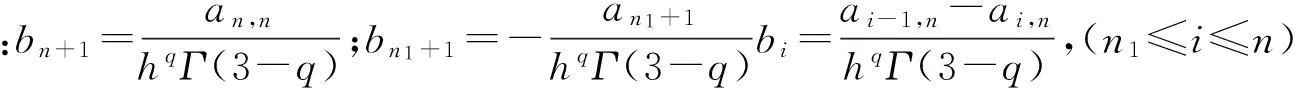
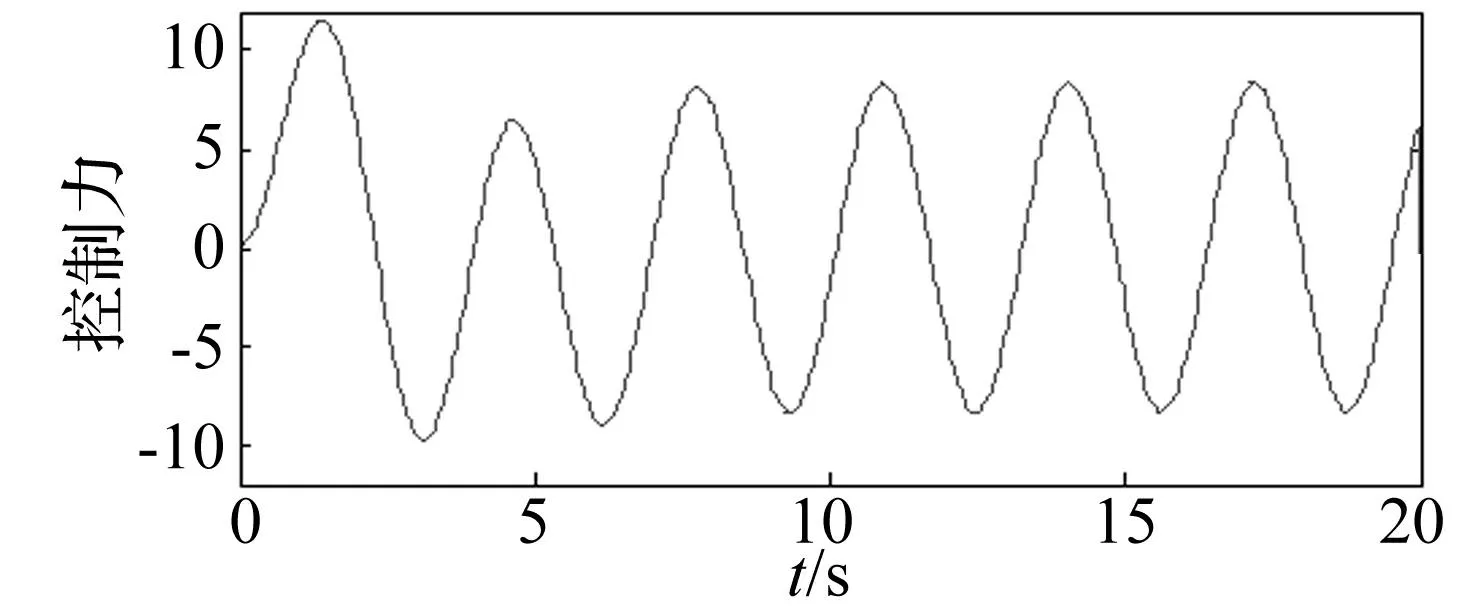
取n-n1=30，令n=200，250，300，式(10)系数见表1。由表1看出，bi

表1　式(10)对于n=200，250，300时系数项

此时可利用靠近计算值处前n2项进行控制器设计，即

Dqxn≈bn+1xn+1+bnxn+…+

bn2+1xn2+1 ,(n2≪n1)

(11)

将式(11)代入式(6)，得

xn+2+(h2c0bn+1-2)xn+1+(h2c0bn+h2k0+1)xn+

h2c0bn-1xn-1+…+h2c0bn2+1xn2+1 =h2F(tn)

(12)

将其变为离散状态方程，即

(13)

式中：X为(n-n2+1)维状态向量；A为(n-n2+1)维矩阵；B，C均为(n-n2+1)向量，均为变换矩阵。

本文以位移为控制对象，兼顾控制力，采用最优控制策略，定义性能指标为

u(kh)Ru(kh)]

(14)

式中：Q为(n-n2+1)维正定权矩阵；R为正数。

通过极小化方程(14)，可得

u(k)=-KX(k)

(15)

K=[BTP(k+1)B+R]-1BTP(k+1)A

(16)

式中：P(k)满足Riccati方程，即

P(k)=[A-BK]TP(k+1)[A-BK]+

(17)

(18)

本文提出调节系数概念，定义实际控制力为

u(k)=-βKX(k)

(19)

式中：β为正调节系数。

此时，式(7)最后两项可重新写为

(20)

D2xn+1=F(tn+1)-KX(n+1)-

c0Dq(xn+1)xn+1-k0D0xn+1

(21)

仍以上算例为例，取n=200，据式(11)前二项进行控制器设计，即

Dqxn≈bn+1xn+1+bnxn=4.2739xn+1+3.5266xn

(22)

式中：

权矩阵取Q=diag[1×1081×108]，R=0.2，则控制增益为K=[63.865 0-31.992 6]，取β=8，则u(k)=-8×(63.865 0xk+1-31.992 6xk)，控制效果见图2(实、虚线分别为控制、未控制时响应)，无量纲控制力见图3。

图2　位移控制效果 Fig.2 Control result of displacement

图3　控制力时程曲线 Fig 3 Dimensionless control force

有关调节系数β的选取，原则上以仿真效果为基础进行调节，建议在0.1～100之间选取。

有关变分数阶系统振动控制研究较少，主要因变分数阶表达式具有渐近累加特点，项数不固定，会对控制器设计造成很大麻烦。

4结论

本文针对由二次函数表示的变分数阶系统，提出基于位移时程拟合的模态截断算法及调节系数概念。研究表明控制效果较好。需要说明的是，本文方法不太适合阶次为x，1+x情况。

参考文献

[1]孙春艳,徐伟. 分数阶导数阻尼下非线性随机振动结构响应的功率谱密度估计[J]. 应用力学学报,2013,30(3):401-405.

SUN Chun-yan,XU Wei. Response power spectral density estimate of a fractionally damped nonlinear oscillator[J]. Chinese Journal of Applied Mechanics, 2013,30(3):401-405.

[2]石星星,周星德,竺启泽,等.建筑结构含分数阶振动控制的最优阶次研究[J]. 振动、测试与诊断,2013,33(2):269-272.

SHI Xing-xing, ZHOU Xing-de,ZHU Qi-ze,et al.Optimal order of fractional-order vibration control of building structure[J]. Journal of Vibration,Measurement & Diagnosis,2013,33(2):269-272.

[3]Saptarshi D, Amitava G, Shantanu D. Generalized frequency domain robust tuning of a family of fractional order PI/PID controllers to handle higher order process dynamics[J]. Advanced Materials Research, 2012, 403: 4859-4866.

[4]Eva K, Seenith S. Non-existence of periodic solutions in fractional-order dynamical systems and a remarkable difference between integer and fractional-order derivatives of periodic functions[J]. Nonlinear Analysis: Real World Applications, 2012,13(3): 1489-1497.

[5]Coimbra C F M. Mechanics with variable-order differential operators[J]. Ann. Phys.,2003,12(11/12): 692-703.

[6]Shyu J J, Pei S C, Chan C H. An iterative method for the design of variable fractional-order FIR differintegrators[J]. Signal Processing, 2009, 89(3): 320-327.

[7]Chan C H, Shyu J J, Yang R H. Iterative design of variable fractional-order IIR differintegrators[J]. Signal Processing, 2010, 90(2): 670-678.

[8]Soon C M, Coimbra C F M, Kobayashi M H. The variable viscoelasticity oscillator[J]. Ann. Phys., 2005,14(6):378-389.

[9]Balachandran K, Park J Y, Anandhi E R. Controllability of fractional integrodifferential systems in banach spaces[J]. Nonlinear Analysis: Hybrid Systems, 2009, 3(4): 363-367.

[10]Diaz G, Coimbra C F M. Nonlinear dynamics and control of a variable order oscillator with application to the van der pol equation[J]. Nonlinear Dynamics, 2009,56(1/2):145-157.

[11]Piotr O, Tomasz R. Variable-fractional-order dead-beat control of an electromagnetic servo[J]. Journal of Vibration and Control, 2008,14(9/10): 1457-1471.