基于双树复小波与非线性时间序列的降噪方法

第一作者胥永刚男，博士，副教授，1975年生

邮箱:xyg@bjut.edu.cn

基于双树复小波与非线性时间序列的降噪方法

胥永刚，赵国亮，马朝永，张建宇

(北京工业大学机电学院先进制造技术北京市重点试验室，北京100124)

摘要：针对双树复小波变换传统软阈值降噪方法对实、虚部树系数分别进行阈值处理时提取的强背景噪声下轴承故障特征信号效果不理想，且实、虚部分离的阈值处理方法会引起局部相位失真问题，利用故障信号小波变换系数具有周期性与双树复小波系数模震荡小等特点，提出双树复小波变换与非线性时间序列方法相结合的强背景噪声下轴承故障特征提取方法。对故障信号进行双树复小波变换，获得各层小波系数并求模，选择系数模周期性较强层系数进行非线性时间序列处理，增强系数中周期性成分，抑制随机噪声；对增强后系数进行软阈值处理消除直流成分对提取结果的影响；将处理后系数还原为复数形式进行双树复小波重构，可成功提取弱故障特征信号。仿真、试验信号处理结果表明，该方法能有效提取强背景噪声下的故障特征信号。

关键词：双树复小波变换；非线性时间序列；软阈值；降噪

基金项目：国家自然科学基金(51375020)；北京市优秀人才培养资助计划(2011D005015000006)；北京市教委科研计划项目(KM201310005013)；北京市属高等学校青年拔尖人才培育计划；北京工业大学基础研究基金

收稿日期：2014-04-01修改稿收到日期：2014-07-16

中图分类号:TH133.3；TH165文献标志码：A

New denoising method based on dual-tree complex wavelet transform and nonlinear time series

XUYong-gang,ZHAOGuo-liang,MAChao-yong,ZHANGJian-yu(Key Laboratory of Advanced Manufacturing Technology, Beijing University of Technology, Beijing 100124, China)

Abstract:A new denoising method based on dual-tree complex wavelet transform and nonlinear time series was proposed, considering the weakness, such as the phase distortion, of the wavelet soft-threshold denoising method, in which the real and image parts of the coefficient are processed individually. The new method process the magnitude of the complex coefficients instead, taking into account the fact that the magnitude does not oscillate in positive and negative directions which is more suitable for threshold denoising and the fact that the coefficients of the fault signal are always periodic. The nonlinear time series method can be used to strengthen the periodicity of the coefficients caused by the fault signal and to restrain the noise meanwhile. In the method proposed, the fault signal was decomposed by dual-tree complex wavelet transform to obtain the coefficients of different layers, the nonlinear time series method was used to strengthen the periodicity of the coefficient, and then the soft-threshold denoising was carried out to remove the DC component. Finally, the fault characteristic signal was obtained by coefficient reconstruction. The simulation and experimental results show the effectiveness of the method, and a new efficient denoising method was provided.

Key words:dual-tree complex wavelet transform (DT-CWT); nonlinear time series; soft threshold; denoising

滚动轴承作为旋转机械的关键组成部分最易发生故障。据统计，旋转机械故障的30%均由轴承故障引起。滚动轴承故障振动信号常表现出非线性非平稳特性，且现场存在强噪声干扰，较难提取滚动轴承故障特征[1]。 因此，研究强背景噪声下滚动轴承故障特征信号的提取方法具有重要意义。

传统离散小波变换(DWT)对非线性非平稳信号的处理效果良好。基于小波变换的降噪方法研究主要集中于小波系数阈值的选取，且较成熟；但由于DWT小波系数震荡剧烈，采用阈值降噪会丢失部分细节信息。双树复小波变换[2]作为传统离散小波变换的改进方法，采用两树滤波器组完成小波分解与重构，较传统方法具有良好的抗频率混叠特性、近似平移不变性与完全重构特性。已成功用于图像处理[3]、语音识别[4]、电力系统[5]及故障诊断[6-8]等。邱爱中[9]通过研究软阈值降噪方法，提出阈值降噪并用于水轮机轴承故障诊断。陈志新[10]对双树复小波的NeighBlock降噪方法进行研究；但均忽略故障特征信号周期性造成小波系数周期性对降噪的重要性。

本文提出基于双树复小波与非线性时间序列的降噪方法，充分利用小波系数的周期性进行强背景噪声信号故障特征提取。仿真、试验信号处理结果证明该方法的可行性、有效性。

1双树复小波变换

双树复小波变换(Dual-tree Complex Wavelet Transform, DT-CWT)采用两树平行近似互为希尔伯特变换对的滤波器进行信号分解与重构，分别称为实部树、虚部树。分解、重构过程中两树滤波器采样频率相同，但要求虚部树采样位置落后实部树采样间隔1/2。半个采样间隔延迟与互为希尔伯特变换对的滤波器性质使实、虚部树联合能更充分利用采样前小波变换系数信息，亦能克服传统离散小波变换的平移不变性差与频率混叠等缺陷，且具有良好的方向选择性、完全重构性及较高计算效率。双树复小波小波函数可表示为

ψ(t)=ψh(t)+iψg(t)

(1)

式中：ψh(t)，ψg(t)为两实小波；i为复数单位。

双树复小波变换由两个并行的实小波变换组成，分解、重构过程见图1。其中h0，h1分别为实部树对应的低、高通滤波器；g0，g1分别为虚部树对应的低、高通滤波器；h0′，h1′为重构时实部树滤波器组；g0′，g1′为重构时虚部树滤波器组。

2非线性时间序列局部投影算法原理

2.1基本原理

非线性时间序列分析方法已成功用于医疗[11]及故障诊断[12-13]等。该方法基本思想为将非线性时间序列进行相空间重构，通过局部投影方法将背景信号、特征信号及噪声投影到不同子空间，抑制时间序列中随机噪声成分，达到分离效果。

设动力系统非线性状态方程为

xk+1=F(xk)

(2)

当F未知时，xk+1可近似为状态xk在{xk},k=1,…,N中u(n)邻域内的线性化估计，即

(3)

不存在噪声时Anxn+bn-xn+1=0，系统处于超平面内；受噪声干扰时yn=xn+ηn，对信号进行相空间重构，噪声处于超平面外的相空间中。可将yn投影到该超平面进行信号消噪。

对任意时间序列sn，可重构m维相空间为

sn={sn(m1)τ,sn(m2)τ,…,snτ,sn}

(4)

式中：τ为延时时间；m为嵌入维数。

该相空间与原系统动力学特性相同，与原系统动力学行为微分同胚。通过sn最小化解对其修正。该投影降噪法称为非线性空间局部投影算法。具体步骤如下：

(1)对时间序列S=s1,s2,…,sn，确定延时时间τ及嵌入维数m，进行m维相空间重构，即

sn={sn-(m-1)τ,sn-(m-2)τ,…,sn}

(5)

(2)确定邻域半径ε，寻找满足‖sk-sn‖∞<ε的向量及个数N。

(3)计算满足条件的N个向量质心，即

(6)

(4)计算协方差矩阵，即

(7)

式中：R为对角权重矩阵，可抑制相点首尾元素产生的畸变。R11，Rmm取较大值，其它Rii=1。

(8)

(6)返回步骤(2)，直到所有相点处理完毕。

修正完毕后将sn中标量信号取平均值即可重构获得降噪后信号，投影多次效果更佳。

2.2参数确定方法

参数选择直接影响算法的降噪效果。延迟时间τ的确定方法有自相关函数法、平均位移法、复自相关法及平均互信息法等。其中自相关函数法与复自相关法较常用。嵌入维数m的确定方法有几何不变量法、虚假邻点法及改进虚假邻点法等。文献[14]对非线性时间序列局部投影算法参数确定的几种常用方法进行总结，并讨论各自计算复杂性与使用便捷性。

本文利用局部投影算法对周期性较明显的小波分解系数进行随机噪声抑制与周期性特征增强。由于处理数据周期性特征较明显，故在确定延迟时间τ时采用自相关函数法。对嵌入维数m，采用效果更好的改进虚假邻点法进行确定，Q一般为3～5。

3DT-CWT与非线性时间序列局部投影算法相结合的降噪方法

通常小波变换系数在信号冲击特征明显处幅值较大，且实小波变换系数在特征明显处出现正负值剧烈交替震荡，给局部投影算法对周期性特征提取造成较大影响，如对延迟时间十分敏感等。信号经双树复小波变换所得小波系数可表示为复数形式，其模在信号冲击特征明显处具有幅值较大特点，且变化较平稳(无剧烈正负值交替震荡)，周期性更明显，使其对延迟时间与嵌入维数的敏感性降低从而更适合非线性时间序列局部投影算法的处理要求。

对系数模进行降噪，利用保留的相位信息可将降噪后的模还原为复数形式，避免对实虚部分别进行阈值降噪再还原为复数所致相位失真现象(在实部树系数较大被保留、虚部树较小归零下出现)。具体实施步骤为：①对信号进行双树复小波变换，获得不同层系数矩阵，计算其模保留相位信息。②选模周期性较明显的层系数及合适的τ，m及Q值进行单次或多次非线性局部投影算法处理。当系数模的周期性不十分明显时，可借助系数谱选择；当系数模存在周期性时其系数谱必定会出现倍频现象。③选取合适阈值对周期增强后的小波系数模进行软阈值处理以消除直流成分对重构信号影响，再利用保留的相位信息还原为复数形式的小波系数。④将处理后的小波系数进行单支重构，即可获得降噪后信号。

4仿真与试验

4.1仿真信号处理效果

单边冲击序列x(t)由10段衰减正弦信号组成，x(t)定义为

(9)

式中：fn=2 000；ζ=0.1。

采样频率10 kHz，每段100点，总点数N=1 000。通过向x(t)添加信噪比为-5 dB高斯白噪声获得噪声污染信号y(t)。x(t)与y(t)的时域波形见图2。由图2可见，y(t)中未发现明显的周期性冲击成分。

将y(t)进行3层双树复小波分解，绘制各层系数模波形，见图3。图中d1～d3为1～3层小波系数模，c3为第3层尺度系数模，由图3看出，d2的周期性较明显，故选择对d2进行降噪。

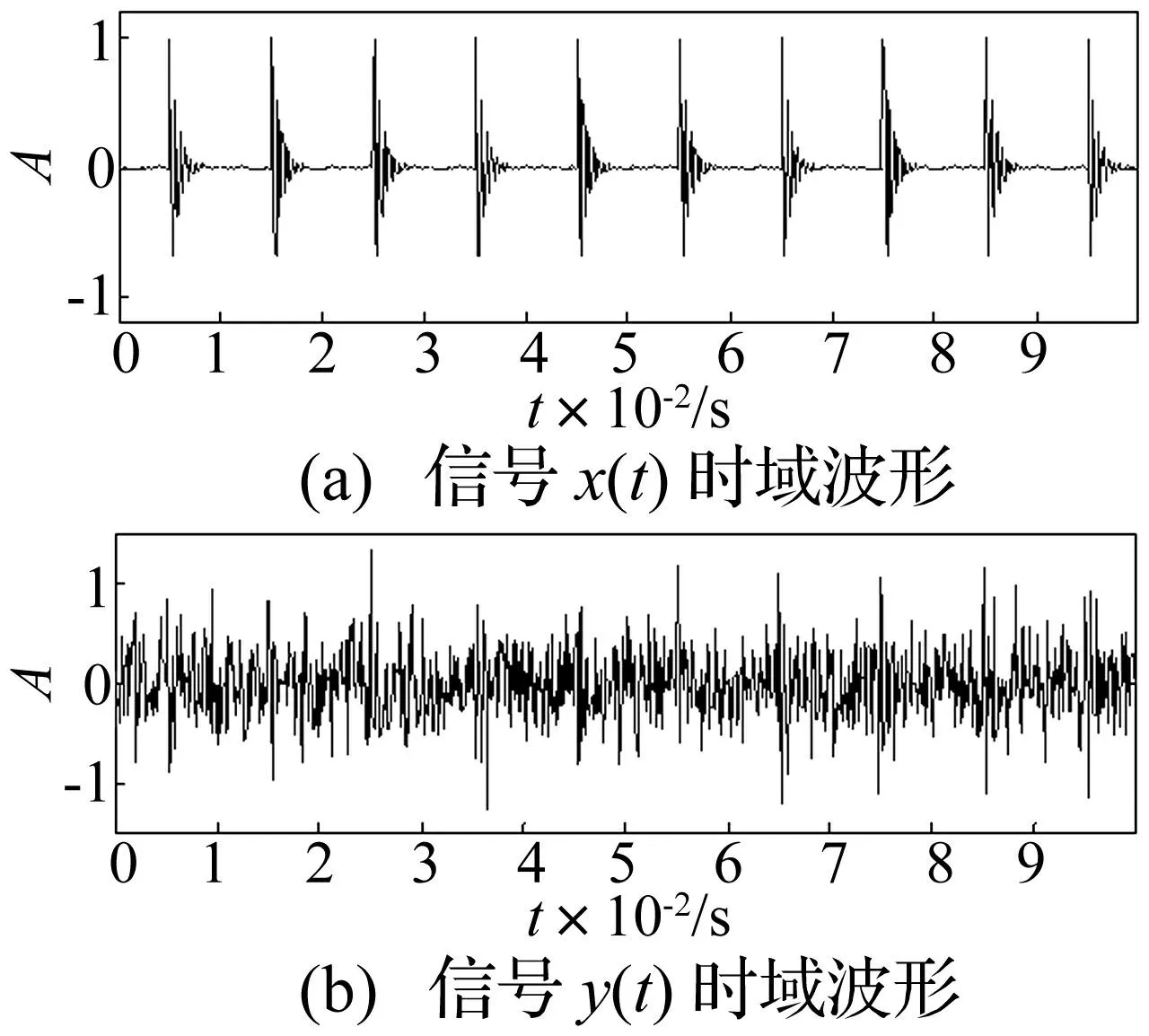
图2　x(t)与y(t)时域波形 Fig.2 Waveform of x(t) and y(t)

图3　双树复小波分解各层系数模 Fig.3 The magnitude of the DT-CWT coefficients

采用自相关函数法获得延迟时间间隔见图4。图中虚线为门限值1-1/e位置，十字线表示自相关函数随时延τ的变化趋势，相关值下降接近该门限值时即为合适的时延时间，本文选τ=6。据改进虚假临近点法(Cao方法)指标E1，E2随嵌入维数变化曲线见图5。由图5看出，选两条线变化平稳、值较接近的点作为嵌入维数即可，故本文选m=13。邻域半径选择方法较简单，只需略大于噪声的平均幅值水平即可，本文选邻域半径ε=0.5。R11，Rmm一般为103，Q=3。

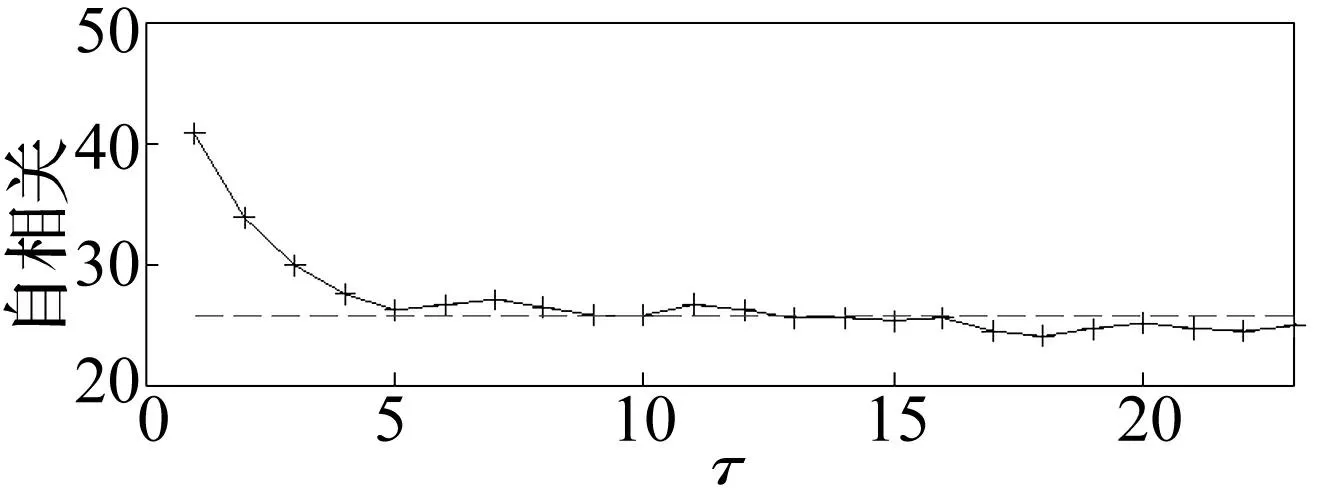
图4　自相关函数法选取延迟时间间隔 Fig.4 Choose the time delay using autocorrelation function

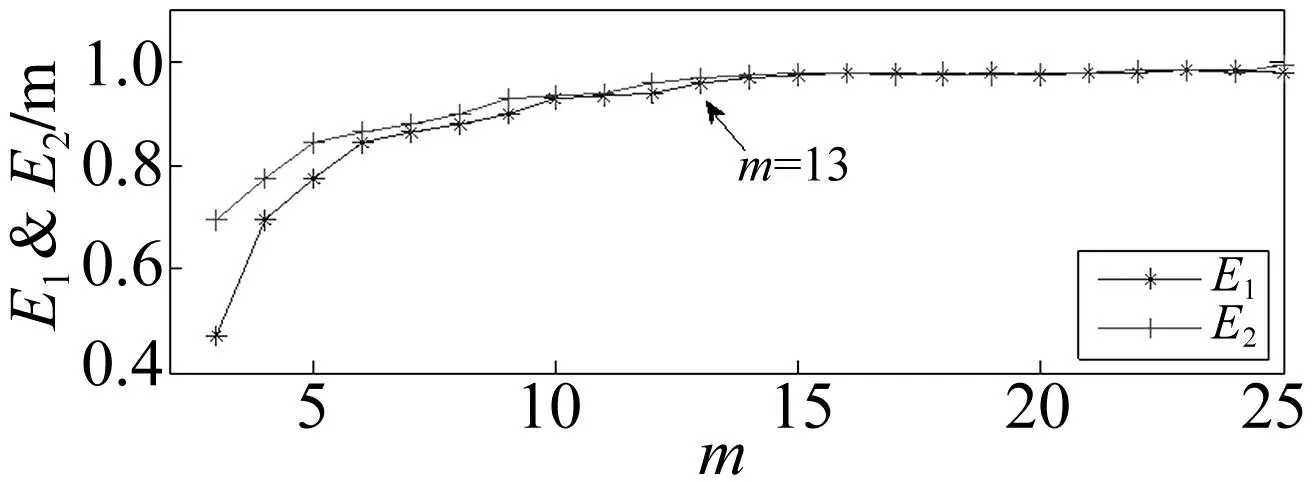
图5　改进虚假邻点法选取嵌入维数 Fig.5 Choose the embedding dimension using Cao method

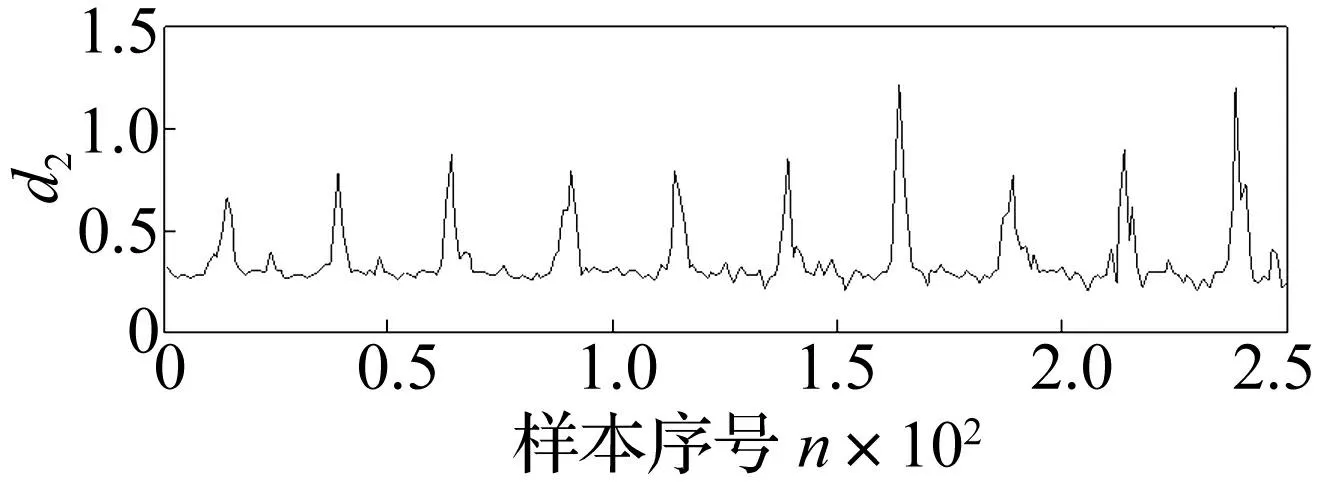
图6　d 2非线性时间序列降噪结果 Fig.6 Denoising result by nonlinear time series

图6为对d2进行两次非线性时间序列局部投影算法降噪结果(参数相同)。由图6发现，d2经投影算法处理后波形中随机冲击成分已明显减少，只保留周期性成分及直流成分(直流分量约0.3)。

为去除直流成分降低其对重构波形干扰，对降噪后的结果进行简单的阈值为0.3的软阈值处理，结果见图7。

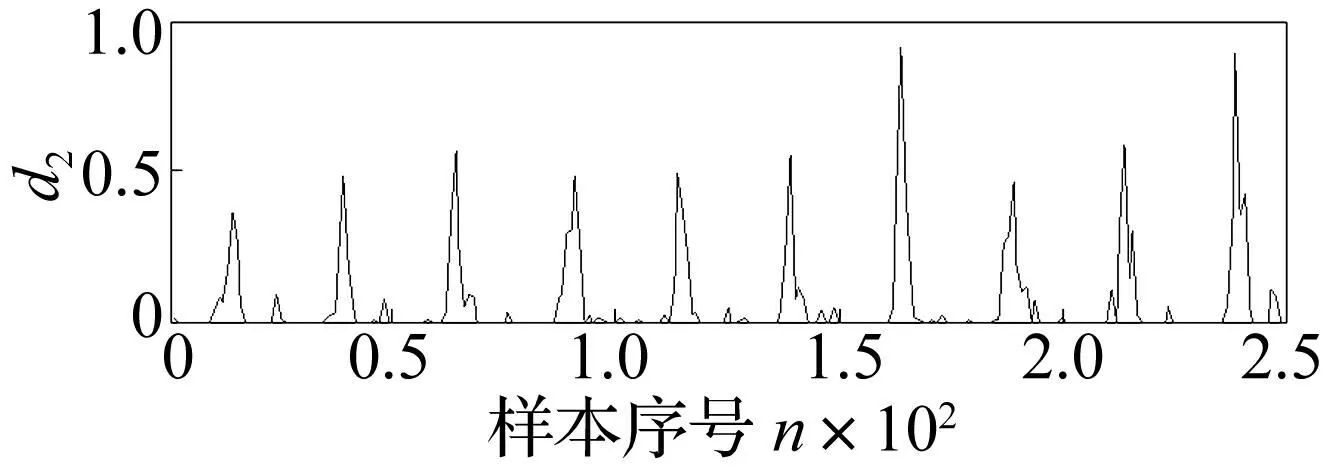
图7　d 2最终降噪效果 Fig.7 The final magnitude of the second layer complex coefficient after denoising

对d2进行单独软阈值处理，结果见图8。其中阈值用Donoho方法[15]计算，即

(10)

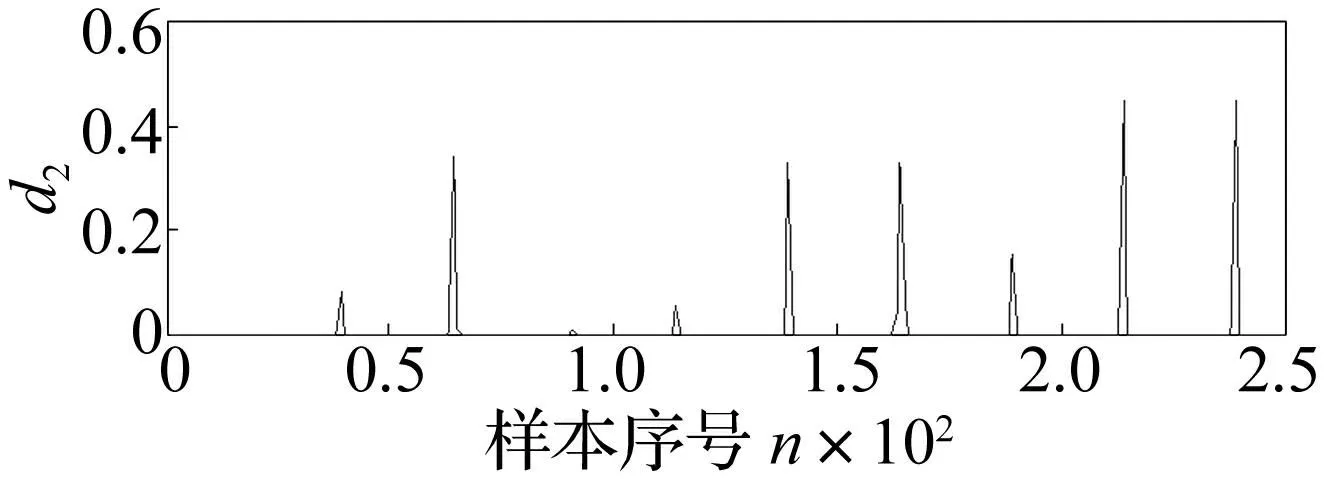
图8　Donoho软阈值降噪 Fig.8 Denoising using Donoho soft-threshold

分别将处理后系数进行重构，获得降噪信号，结果见图9。由图9看出，时域波形方面，d2直接重构信号虽出现周期性冲击特征，但仍含较强噪声；软阈值降噪结果虽保留部分冲击特征，但大部分冲击特征与背景噪声被一并去除，不能达到良好的降噪效果；基于非线性时间序列的降噪方法在去除强背景噪声的同时更完整保留故障特征信号，较传统软阈值降噪方法降噪效果更好。该效果可用信噪比定量评价，即

(11)

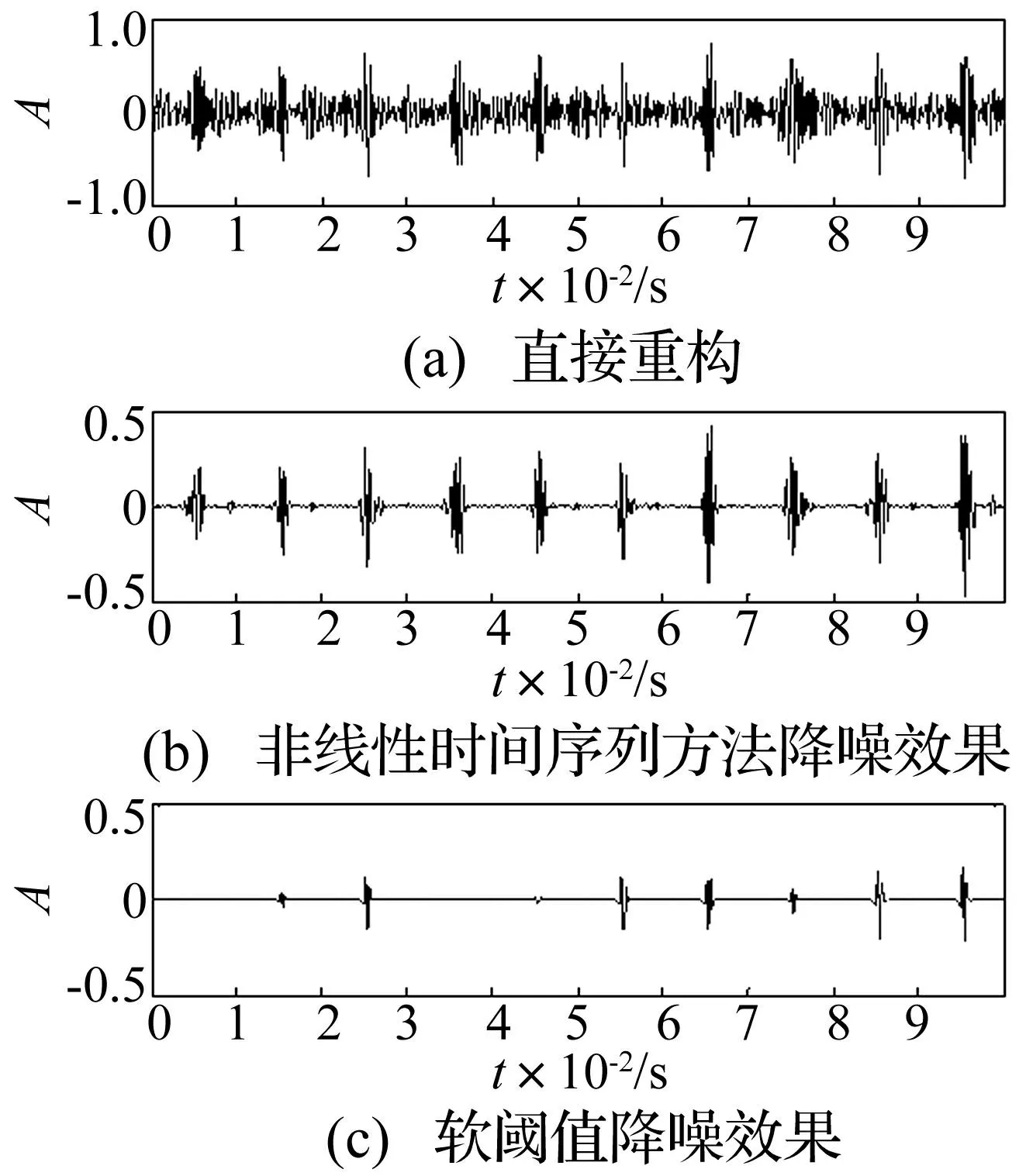
图9　非线性时间序列与软阈值降噪效果对比 Fig.9 Comparison of the noise reduction effect based on nonlinear time series and soft-threshold

图9中3种信号相对x(t)信噪比见表1，对比发现，本文方法所得信号信噪比更高，降噪效果更好。

表1　降噪效果对比

4.2试验信号处理效果

试验系统包括轴承试验台、压电式加速度传感器及数据采集仪。滚动轴承故障模拟试验台结构见图10。试验台滚动轴承型号为6307，传感器垂直安装于末端轴承座。通过末端轴承座内分别安装正常轴承及模拟故障轴承获取试验台正常及轴承模拟故障下振动信号。

图10　轴承试验台 Fig.10 Rolling bearing test rig

为模拟轴承外圈裂纹故障，利用线切割技术在正常轴承外圈滚道加工宽约0.5 mm，深0.5 mm凹槽。试验时，电机转速为1 496 r/min，采样频率设为15 360 Hz，采样点数2 048。所得外圈裂纹模拟故障振动信号见图11，可见无明显周期性冲击。

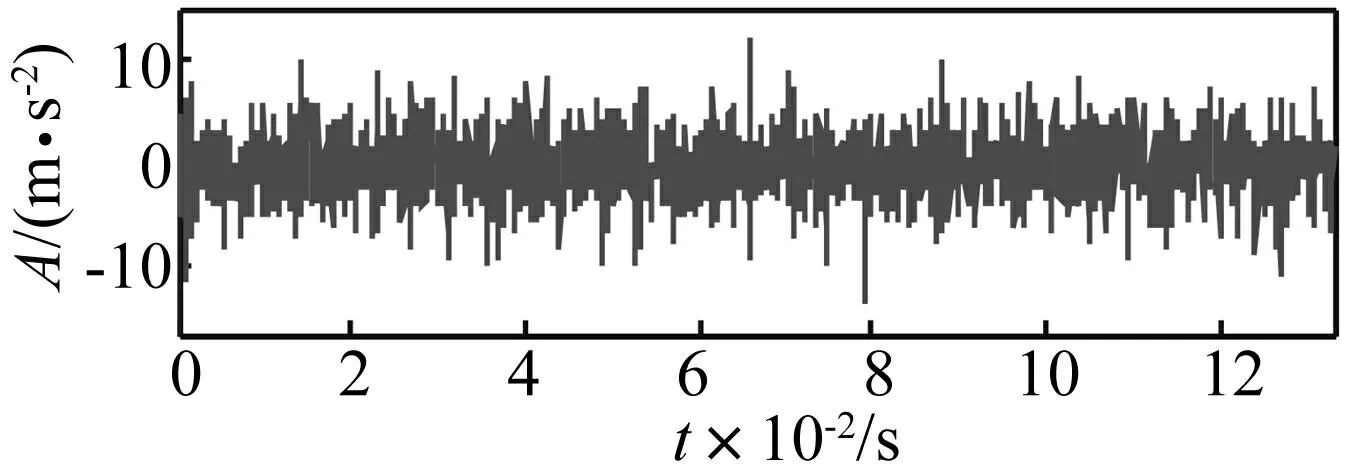
图11　外圈故障模拟信号 Fig.11 Outer ring fault simulation signal

利用DT-CWT对试验信号进行3层分解，获得3层小波系数及第3层尺度系数，见图12。其中，d1～d3分别为第1～3层小波系数模，c3为第3层尺度系数模。由图12看出，各层小波系数与尺度系数模无明显的周期性。

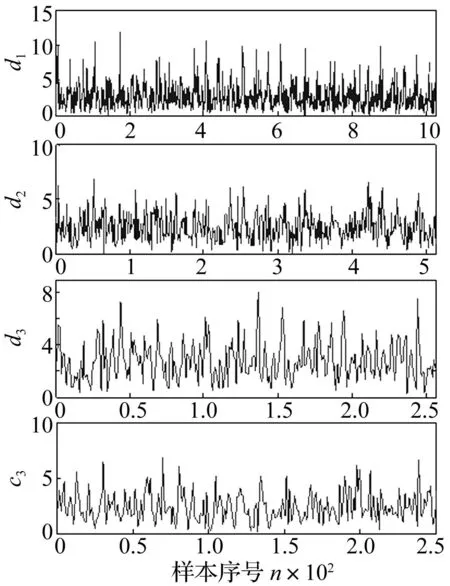
图12　小波系数与尺度系数模 Fig.12 The magnitude of the detail coefficients and approximation coefficients computed using DT-CWT

求得各层系数模的系数谱见图13。由图13看出，d1的系数谱呈现倍频特征，预示其存在周期性特征，故选d1分别进行非线性时间序列局部投影算法及单独软阈值处理。

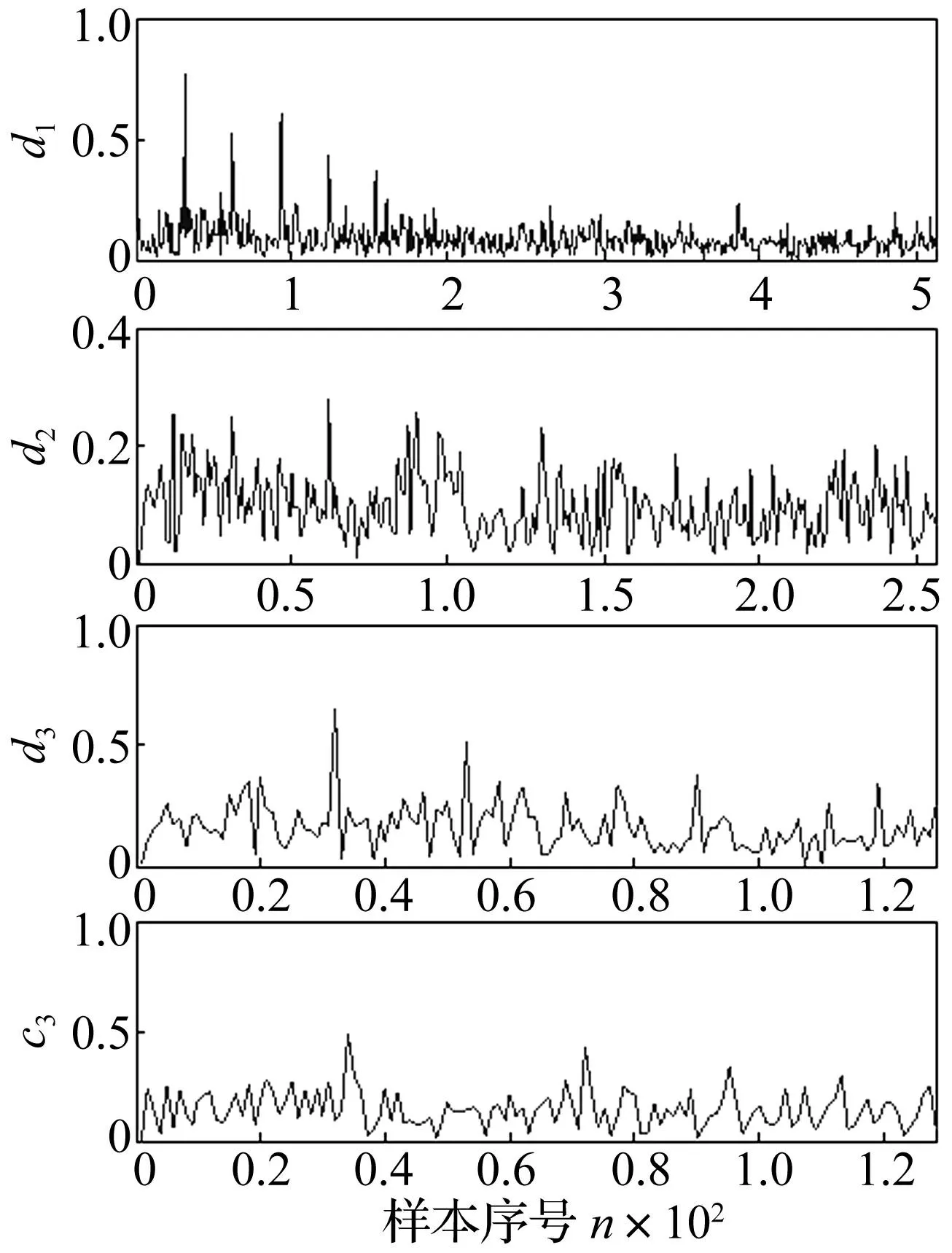
图13　小波系数与尺度系数系数谱 Fig.13 Spectrum of the detail coefficients and approximation coefficients

分别利用自相关函数法与改进虚假临近点法确定延迟时间及嵌入维数，即τ=100，m=10。邻域半径ε=5，Q=3。通过分析处理结果可确定软阈值处理过程阈值为3。经计算单独Donoho软阈值处理的阈值为3。处理结果见图14。

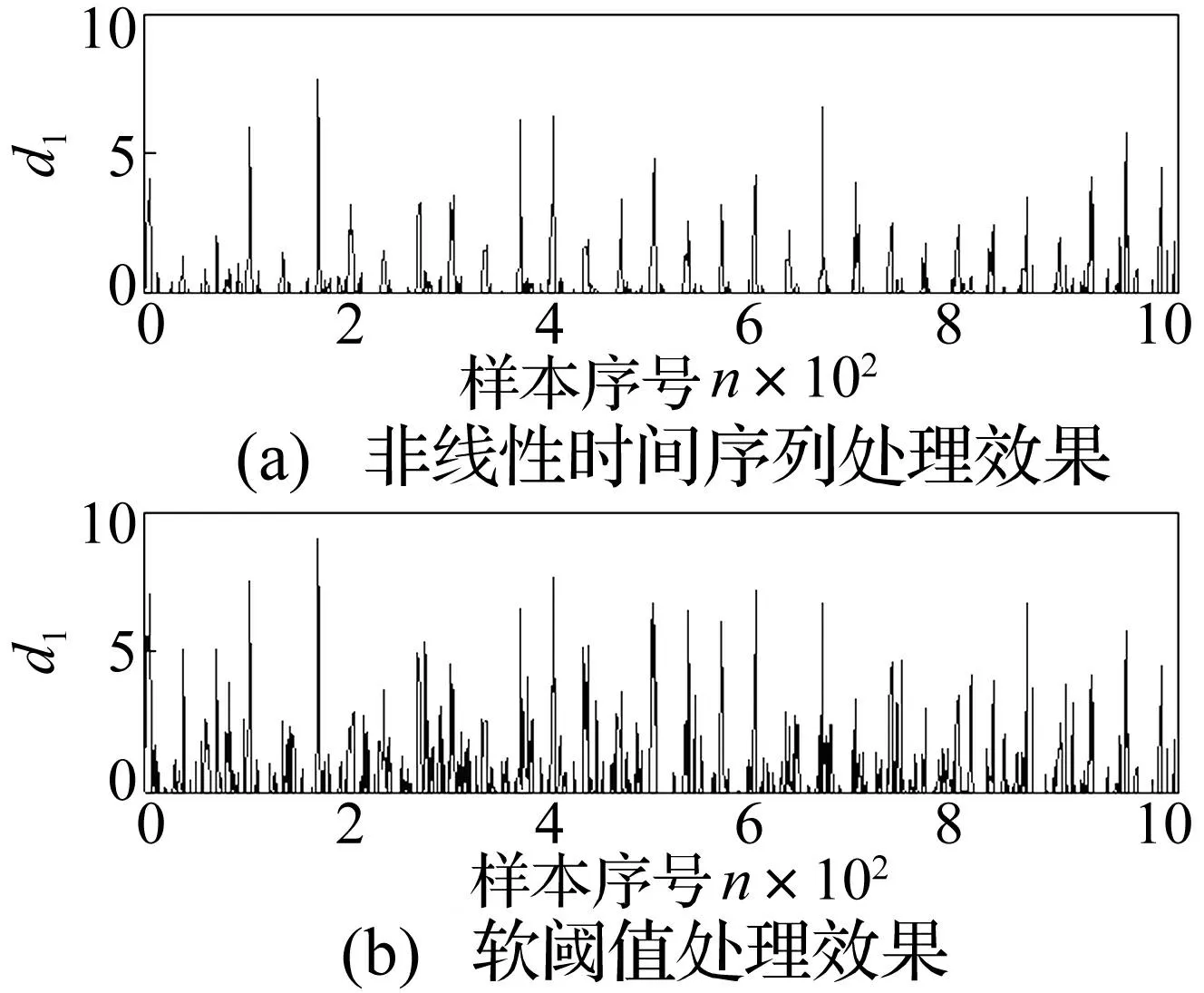
图14 　d 1非线性局部投影算法与单独软阈值降噪效果 Fig.14 Comparison of the coefficients noise reduction effect based on nonlinear time series and soft-threshold

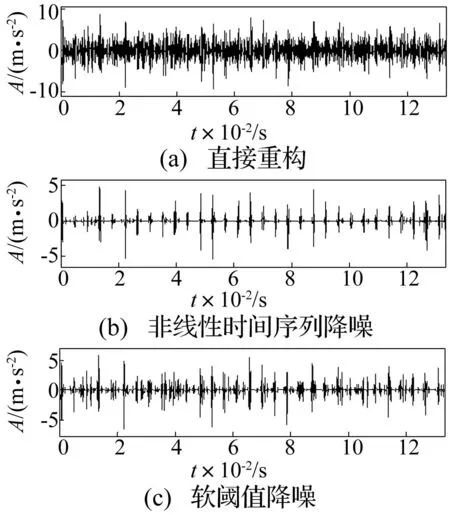
图15　降噪效果对比 Fig.15 Comparison of the noise reduction effect based on nonlinear time series and soft-threshold

将处理的系数模还原为小波系数，进行双树复小波重构，获得降噪后信号见图15。由图15看出，直接重构信号仍存在较强的背景噪声，由于故障频带内含较强烈背景噪声，单独双树复小波单支重构降噪方法并不能成功提取强背景噪声下的故障特征信号；软阈值降噪方法降噪效果同样不理想，难以分辨是否存在周期性冲击；本文的基于双树复小波与非线性时间序列降噪方法能在去除强背景噪声同时较完整保留弱冲击故障特征，成功提取到强背景噪声下故障特征信息，降噪效果明显优于传统软阈值降噪方法。

5结论

通过研究双树复小波变换与非线性时间序列局部投影方法相结合的轴承故障特征信号提取，利用故障特征信号引起的小波系数周期性实现强背景噪声下故障特征提取，结论如下：

(1)双树复小波变换的小波系数模能更准确反映信号中周期性冲击成分；可利用故障频带所处层小波系数的周期性进行故障特征信号提取。

(2)非线性时间序列局部投影算法能提取小波系数的周期性成分，有效降低系数中随机噪声，进而从小波系数层面进行降噪。

(3)将双树复小波变换与非线性时间序列局部投影方法相结合能有效提取强背景噪声中轴承故障特征信号，较传统软阈值降噪方法降噪效果更好，同时亦为小波系数降噪提供了新方法。

参考文献

[1]杨国安. 滚动轴承故障诊断实用技术[M]. 北京：中国石化出版社，2012：13-17.

[2]Selesnick I W, Baraniuk R G, Kingsbury N G. The dual-tree complex wavelet transform[J]. IEEE Digital Signal Processing Magazine, 2005, 22(6): 123-151.

[3]Snekhalatha U, Anburajan M. Dual tree wavelet transform based watershed algorithm for image segmentation in hand radiographs of arthritis patients and classification using BPN neural network[C]. Information and Communication Technologies(WICT),World Congress on, IEEE, 2012: 448-452.

[4]王娜,郑德忠,刘永红. 双树复小波包变换语音增强新算法[J]. 传感技术学报,2009,22(7):983-987.

WANG Na, ZHENG De-zhong, LIU Yong-hong. New method for speech enhancement based on dual tree complex wavelet packet transform[J]. Journal of Sensors and Actuators, 2009, 22(7): 983-987.

[5]季晨宇,袁振海. 基于双树复小波的行波选线选相法[J].电力系统保护与控制,2011,39(12)：48-54.

JI Chen-yu, YUAN Zhen-hai. Fault line and phase selection based on traceling wave and dual-tree complex wavelet[J]. Power System Protection and Control, 2011, 39(12): 48-54.

[6]苏文胜,王奉涛,朱泓，等. 双树复小波域隐Markov树模型降噪及在故障诊断中的应用[J]. 振动与冲击,2011,30(6)：47-52.

SU Wen-sheng, WANG Feng-tao, ZHU Hong, et al. Denoising method based on hidden Markov tree model in dual tree complex wavelet domain and its application in mechanical fault diagnosis[J]. Journal of Vibration and Shock, 2011,30(6): 47-52.

[7]胥永刚,孟志鹏,陆明,等. 基于双树复小波和奇异差分谱的齿轮故障诊断研究[J]. 振动与冲击,2014,33(1)：11-16.

XU Yong-gang, MENG Zhi-peng, LU Ming, et al. Gear fault diagnosis based on dual-tree complex wavelet transform and singular value difference spectrum[J]. Journal of Vibration and Shock, 2014, 33(1): 11-16.

[8]陈彬强,张周锁,何正嘉. 双密度双树复小波变换及其在机械故障微弱特征提取中的应用[J]. 机械工程学报,2012, 48(9): 56-63.

CHEN Bin-qiang, ZHANG Zhou-suo, HE Zheng-jia. Enhancement of weak feature feature extraction in machinery fault diagnosis by using double density dual tree complex wavelet transform[J]. Journal of Mechanical Engineering, 2012, 48(9): 56-63.

[9]邱爱中. 对偶树复小波阈值降噪法及在机械故障诊断中的应用[J]. 机械传动，2011，35(9)：58-61.

QIU Ai-zhong. A new denoising method of DT-CWT and its application in mechanical fault diagnosis[J]. Journal of Mechanical Transmission, 2011, 35(9): 58-61.

[10]陈志新. 对偶树复小波分析及其在故障诊断中的应用[D]. 北京：北京科技大学，2007.

[11]任明荣,王晨,方滨,等. 基于非线性时间序列的胎儿心电信号提取算法[J]. 系统仿真学报,2009，21(16)：5006-5008.

REN Ming-rong, WANG Chen, FANG Bin, et al. Fetal ECG extraction algorithm based on nonlinear time series[J]. Journal of System Simulation, 2009, 21(16): 5006-5008.

[12]阳建宏,徐金梧,杨德斌,等. 邻域自适应选取的局部投影非线性降噪方法[J]. 振动与冲击,2006,25(4)：64-67.

YANG Jian-hong, XU Jin-wu, YANG De-bin, et al. Nonlinear noise reduction method by local projection with adaptive neighborhood selection[J]. Journal of Vibration and Shock, 2006, 25(4): 64-67.

[13]黄艳林,李友荣,肖涵,等. 基于相空间重构与独立分量分析的局部独立投影降噪算法[J]. 振动与冲击,2011,30(1)：33-36.

HUANG Yan-lin, LI You-rong, XIAO Han, et al. Local independent projection de-noising algorithm based on phase-space reconstruction technique and independent component analysis[J]. Journal of Vibration and Shock, 2011,30(1): 33-36.

[14]王晨. 基于非线性时间序列的胎儿心电信号分析与提取[D]. 北京:北京工业大学,2009.

[15]Donobo D L. De-noising by soft-thresholding[J]. Transactions on Information Theory, 1995, 41(3): 613-627.