深水缓波形脐带缆结构响应及参数敏感性分析

深水缓波形脐带缆结构响应及参数敏感性分析

宋磊建1，韩芸2，付世晓1,李梨3

(1. 上海交通大学海洋工程国家重点实验室，上海200240； 2. 中国船舶及海洋工程设计研究院，上海200011；3.上海江南长兴造船有限责任公司，上海201913)

摘要：对某采用缓波形布局的深水脐带缆进行静态分析，得到了脐带缆的整体结构响应，包括脐带缆初始线形、有效张力和弯曲曲率的分布特性。同时对脐带缆缓波形布局下的总体布局参数进行了参数敏感性分析，得到了浮子段长度、浮力因子、浮子段起始位置及顶部悬挂角对脐带缆结构响应的影响。这些研究结果可以为深水脐带缆的缓波形布局设计提供参考。

关键词：脐带缆；缓波形；结构响应；敏感性分析

中图分类号:TH212；TH213.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.017

Abstract:Here, the structural responses of a Lazy-wave deepwater umbilical were obtained including configuration, distributions of effective tension and curvature with the static analysis. Meanwhile, the sensitivity analysis of the general layout parameters including length of buoyancy catenary, buoyancy factor, starting location of buoyancy catenary and top hang-off angle was performed and the influences of the general layout parameters on the structural response of the umbilical were analyzed. These study results provided a reference for Lazy-wave configuration design of deepwater umbilicals.

基金项目：国家自然科学基金(11472107)资助项目

收稿日期：2014-08-19修改稿收到日期：2014-10-17

Structural responses and parameter sensitivity analysis of a Lazy-Wave deepwater umbilical

SONGLei-jian1,HANYun2,FUShi-xiao1,LILi3(1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;2. Marine Design & Research Institute of China, Shanghai 200011, China;3. Shanghai Jiangnan Changxing Shipbuilding Co., LTD, Shanghai 201913, China)

Key words:umbilical; Lazy-wave; structural responses; sensitivity analysis

脐带缆是连接平台或浮式生产系统与海底油井的控制管缆，主要功能是化学药剂(如甲醇、乙醇)的注入、水压的控制、信号的控制、电力的控制等。脐带缆一般悬挂于平台或浮式结构底部，脐带缆底部与水下终端相连，其受到的主要荷载为自重引起的拉伸荷载和波浪、流以及船体运动作用导致缆在水中运动所产生的动态弯曲荷载[1]。脐带缆由于其典型的柔性特征以及复杂的环境载荷，其设计和分析一直受到极大的关注。

在深海脐带缆和深海立管等柔性管线的设计中，管线的布局形式在很大程度上决定着其承受载荷的大小。悬链线布局与缓波形布局是深海管线常用的两种布局形式。悬链线布局具有结构简单，施工方便，成本较低，无需张力补偿，对浮体运动有较大的适应性等优点，但是随着工作水深的增加，管线长度和重量会相应的增加，顶部悬挂点处的张力会很大，从而对张紧器的要求提高，且在恶劣的环境下或者顶部平台运动剧烈时，立管触地点处的疲劳损伤很大[2-5]。而缓波形布置可以减小悬挂点处的张力，减小顶部平台运动和波浪对触地点的影响，提高触地点的疲劳寿命[6-9]。随着海洋油气的开采不断走向深水，缓波形布局将会得到越来越多的应用。

在立管和脐带缆的设计中，静态分析具有很重要的作用。一方面，在进行动态分析之前需要先进行静态分析，只有静态分析的结果满足设计要求才能继续下一步的工作；另一方面，一般来讲，动态响应大于静态响应，静态分析得到的结果与设计要求之间有15%～30%以上的差额时，其动态响应结果才有可能满足设计要求[10]。本文对某采用缓波形布局的深水脐带缆进行静态分析以及参数敏感性分析，得到深水脐带缆在缓波形布局下的整体结构响应，包括：脐带缆的初始线形、有效张力和弯曲曲率，以及浮子段长度、浮力因子、浮子段起始位置和顶部悬挂角对脐带缆整体结构响应的影响。

1深水缓波形脐带缆线形分布及计算模型

1.1缓波形脐带缆线形分布理论分析

深水脐带缆缓波形布局整体线形分布见图1。在缓波形布局下，脐带缆可以分为四段：悬垂段AC、浮子段CE、下降段EF以及流线段FG。其中悬垂段又可以分为悬挂段AB和跳接段BC，浮子段分为升举段CD和拖曳段DE。图1中的H为脐带缆的工作水深，θ为顶部悬挂角。

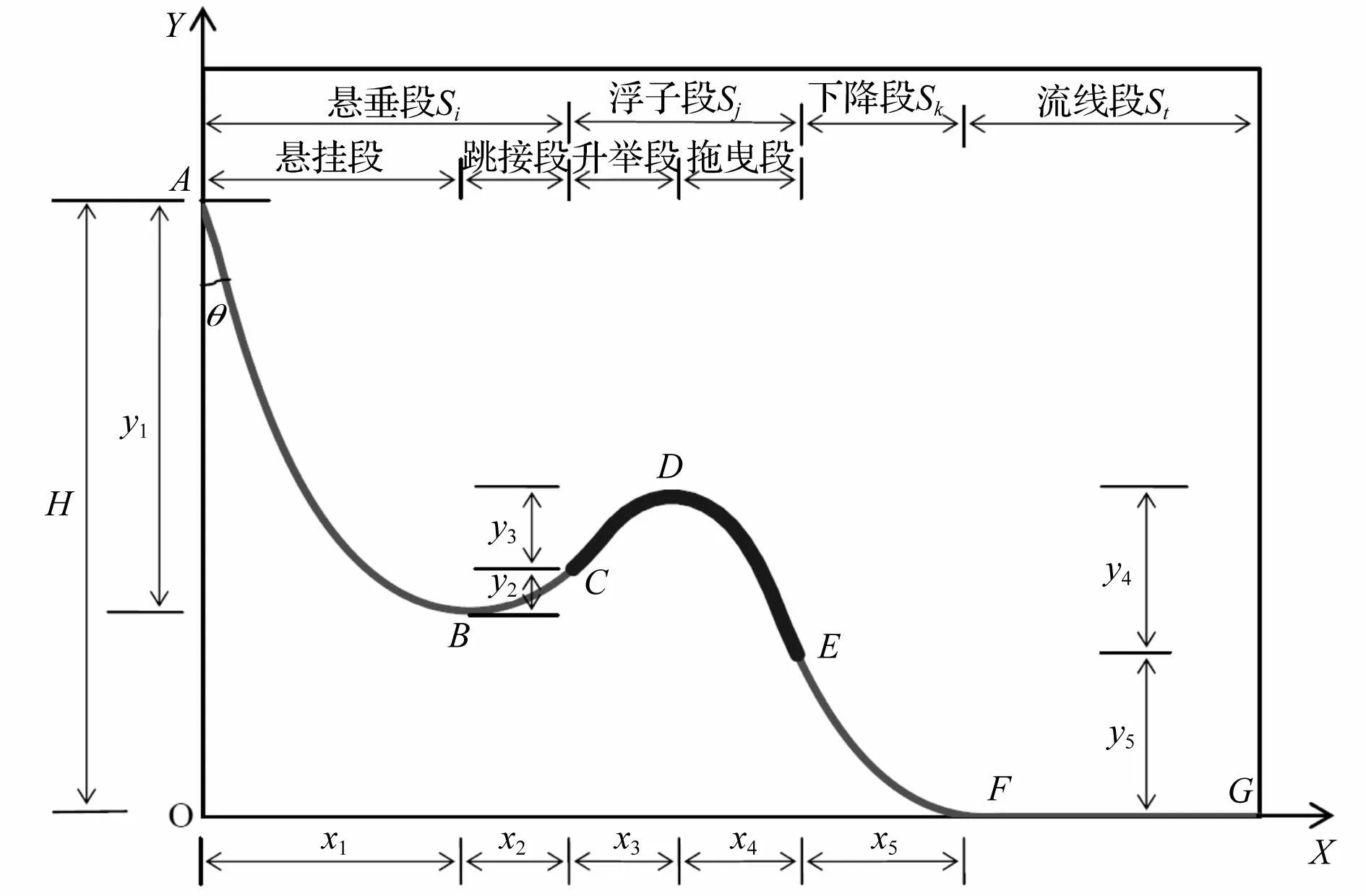
图1　缓波形脐带缆整体线形分布 Fig.1 Configuration of the Lazy-wave umbilical

缓波形脐带缆的悬挂段AB、跳接段BC、升举段CD和拖曳段DE以下降段EF可以看作为自由悬挂的悬链线[11]。若已知悬垂段AC、浮子段CE、下降段EF的长度：Si、Sj和Sk及管线单位长度的湿重w和浮子段的湿重wf，即可以算出根据悬链线理论可以得到悬挂段AB、跳接段BC、升举段CD、拖曳段DE以及下降段EF线形的水平跨距和垂直高度，即为：x1～x5和y1～y5,见图1，同时点B、点D和点F处的曲率ai、aj、ak也可以求得，各参数的表达式如下：

x1=aiarcsinh(cotθ)

y1=ai(cosh(x1/ai)-1)

(1)

x2=aiarcsinh(Si/ai-cotθ)

y2=ai(cosh(x2/ai)-1)

(2)

x4=-aiwfarcsinh(Sk/ai)/w

(3)

x3=-x2wf/wy3=-y2wf/w

(4)

x5=-x4w/wfy5=-y4w/wf

(5)

ai=ak=(Si+Sk-nSj)tanθaj=-aiwf/w

(6)

从图1中可以得到脐带缆顶部悬挂点到底部触地点的垂直高度H，如下式：

H=y1+y4+y5-y2-y3

(7)

在管线的缓波形布局设计中，一般给出的参数为顶端悬挂点的水深h，即顶部悬挂点到底部触地点的垂直高度H，顶端悬挂角θ，管线单位长度的湿重w，悬挂段长度Si，浮子段的长度Sj以及浮力块的直径、密度等参数，下降段的长度Sk是不知道的，因此为了得到缓波形的线形布局，需要根据式(1)～式(7)进行迭代计算，得到下降段的长度Sk以及x1～x5，y1～y5和ai、aj、ak。脐带缆的整体线形分布可表示为：

1.2深水缓波形脐带缆计算模型

本文计算所选取的深水脐带缆在缓波形布局下的关键参数见表1。脐带缆的工作水深为1300m。

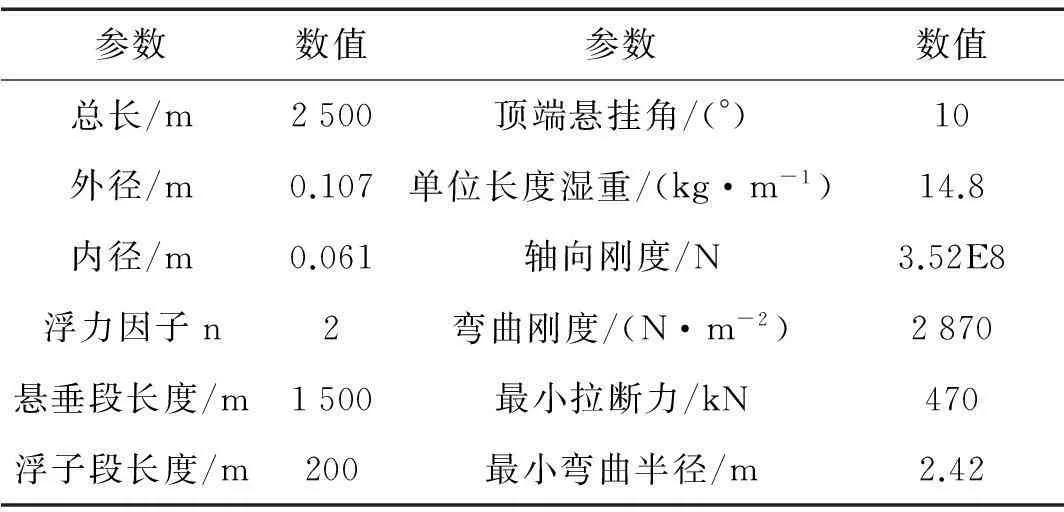
表1　缓波形脐带缆的关键参数

浮力因子n的定义如下：

n=-wf/w

(1)

式中，w为脐带缆单位长度裸缆的湿重，wf为带浮力块的浮子段单位长度的湿重，其为负值。浮力因子的大小表征了单位长度浮力段提供的浮力大小，浮力因子越大，单位长度浮力段提供的浮力越大。根据浮力因子n的定义，即可由上表1得到脐带缆在缓波形布局下浮子段单位长度的湿重。

利用表1中的参数结合式(8)计算得到脐带缆在缓波形布局下的线形分布，包括脐带缆顶部端点和底部端点的坐标，然后在软件OrcaFlex中建立此脐带缆在缓波形布局下的有限元模型，见图2。脐带缆模型的悬垂段、下降段和流线段采用Line单元，浮子段采用Line 单元中Buoyancy modules attached to a line(Line with Floats)方法进行模拟[12]，模型的顶部悬挂在Spar平台模型上，底部固定在海床上，模型顶部和底部的连接方式均为铰接，故模型的两端均可自由转动。

图2　缓波形脐带缆有限元模型 Fig.2 FEM of Lazy-wave umbilical

2深水脐带缆缓波形布局整体结构响应分析

利用建立的有限元模型对脐带缆进行静态分析，得到脐带缆的线形分布,见图3。脐带缆有效张力的分布见图4。从图4中可以看出，在缓波形布局下，由于浮子段浮力的作用，脐带缆有效张力的基本变化趋势为先减小后增大再减小，从而导致在顶部悬挂点以及浮子段的末尾点出现张力极大值。有效张力的最大值则出现在顶部悬挂点处。在流线段上，有效张力减小的原因为在计算时考虑了海底摩擦对脐带缆的作用。

脐带缆弯曲曲率的分布见图5。从图5中可以看出，缓波形布局下，脐带缆弯曲曲率的极大值点有3个，分别为悬垂段上悬挂段的末端、浮子段上升举段的末端以及触地点。弯曲曲率的最大值则出现在浮子段上升举段的末端，而不是出现在触地点上，这与悬链线布局是不一致的， 这是由于浮子段提供的浮力使得浮子段产生大的局部弯曲变形导致的。

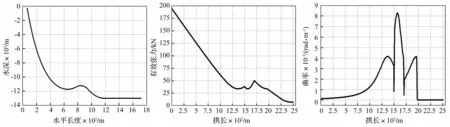
图3 缓波形脐带缆初始线形分布Fig.3ConfigurationofLazy-waveumbilical图4 缓波形脐带缆有效张力分布Fig.4EffectivetensionofLazy-waveumbilical图5 缓波形脐带缆弯曲曲率分布Fig.5CurvatureofLazy-waveumbilical

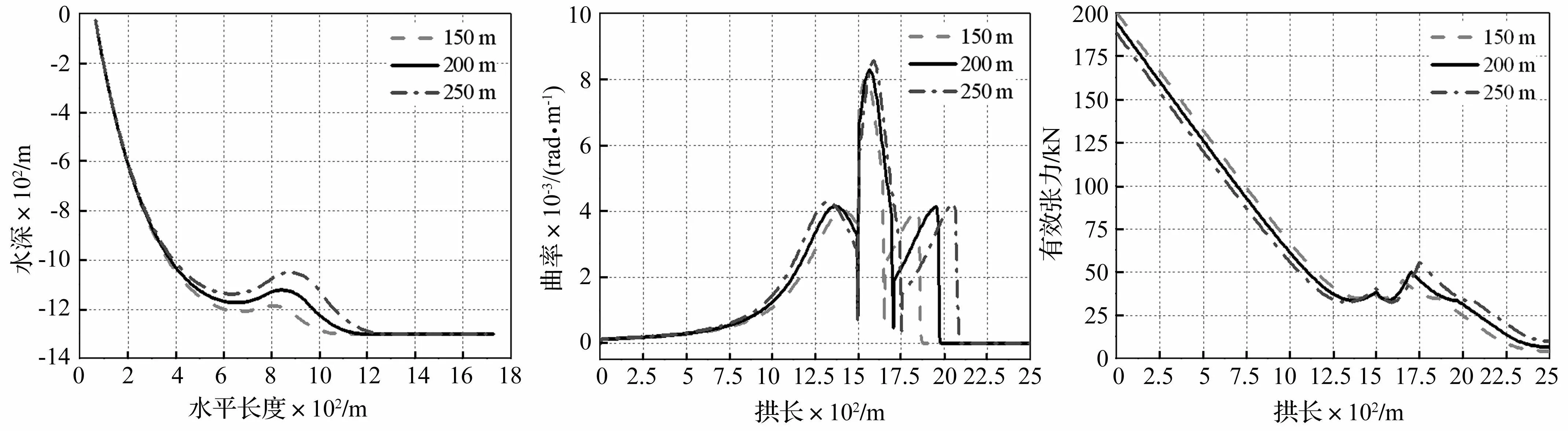
图6 浮子段不同长度下脐带缆初始线形Fig.6Configurationfordifferentlengthsofthebuoyancycatenary图7 浮子段不同长度下脐带缆弯曲曲率Fig.7Curvaturefordifferentlengthsofthebuoyancycatenary图8 浮子段不同长度下脐带缆有效张力Fig.8Theeffectivetensionfordifferentlengthsofthebuoyancycatenary

3深水脐带缆缓波形布局参数敏感性分析

3.1浮子段长度的参数敏感性分析

为了研究浮子段长度对深水脐带缆结构响应的影响，保持其余参数不变，计算浮子段长度为150m、200m和250m时脐带缆的静态响应，得到不同浮子段长度下脐带缆的线形分布，见图6。从图中可以看出，浮子段越长，其提供的浮力越大，脐带缆的波形越陡。相应的，脐带缆弯曲曲率的最大值也越大，见图7和表2。

表2　浮子段不同长度下最大张力和最大曲率

浮子段长度对脐带缆有效张力的影响见图8。从图中可以看出，当浮子段起始位置不变，浮子段的长度增大时，其提供的浮力变大，减小了脐带缆对顶部悬挂点处张力的需求，从而使得顶部悬挂点处脐带缆的最大有效张力减小，见表2。但是由于浮力的增大，使得脐带缆的下降段增长，从而使得浮子段末尾处以及下降段上的有效张力变大。

3.2浮力因子的参数敏感性分析

为了研究浮力因子对脐带缆结构响应的影响，保持其他参数不变，计算浮力因子为2、3、4时脐带缆的静态响应，得到浮力因子对脐带缆初始线形的影响,见图9。从图中可以看出，当浮力因子增大时，脐带缆的波形变陡，从而导致脐带缆最大弯曲曲率变大，见图10和表3。从图10和表3中还可以发现，脐带缆浮子段上的弯曲曲率对浮力因子的变化很敏感，在设计中，应注意浮力因子的选取，防止因浮力过大导致浮子段上发生过大的弯曲。

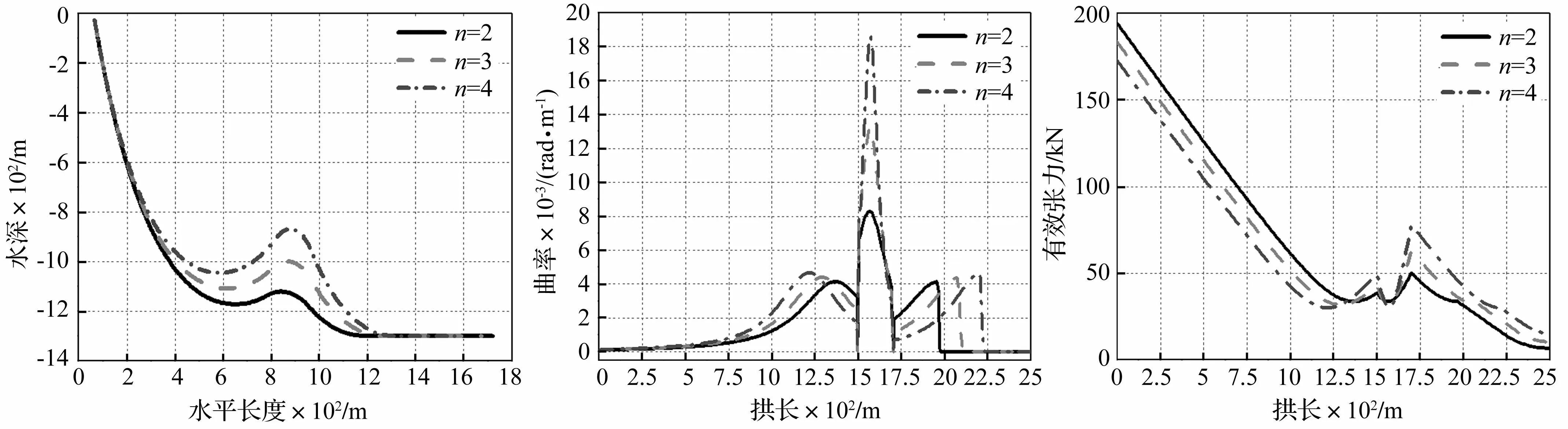
图9 不同浮力因子下脐带缆初始线形Fig.9Configurationfordifferentbuoyancyfactors图10 不同浮力因子下脐带缆弯曲曲率Fig.10Curvaturefordifferentbuoyancyfactors图11 不同浮力因子下脐带缆有效张力Fig.11Effectivetensionfordifferentbuoyancyfactors

表3不同浮力因子下脐带缆最大张力和曲率

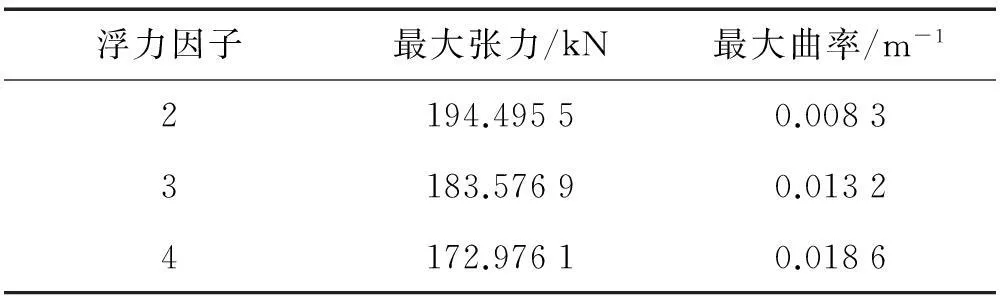
Tab.3 Max tension and curvature for different buoyancy factors

图11给出了浮力因子对脐带缆有效张力分布的影响。从图11中可以看出，当浮力因子增大时，脐带缆的最大张力，即顶部悬挂点处的有效张力减小，而浮子段末端的有效张力增大。这符合实际情况，因为浮力因子越大，浮子段提供的浮力也越大，从而减小对顶部悬挂点处张力的需求。同时，浮力因子越大，脐带缆下降段的长度也越大(见图9)，使得下降段对浮子段末尾处的拉力增大，从而使得浮子段末尾处的有效张力变大。

3.3浮子段起始位置的参数敏感性分析

浮子段起始位置为浮子段的起点与顶部悬挂点间脐带缆的长度，也就是悬垂段的长度。为了研究浮子段起始位置的参数敏感性，保持其他参数不变，计算当浮子段起始位置分别为：1400m、1500m和1600m时脐带缆的静态响应，得到不同浮子段起始位置下脐带缆的初始线形分布，见图12。从图12中可以发现，浮子段的起始位置越大，脐带缆顶部悬挂点距底部触地点之间的水平跨距越大，脐带缆的波形越缓。相应的，最大弯曲曲率随着浮子段起始位置的增大而减小，见图13和表4。在水平跨距为700～1000m处大致为脐带缆的浮子段区域，从图12可以看出，浮子段起始位置越大，脐带缆浮子段区域的跨距越大，波形越缓，从而导致浮子段上的曲率变小，见图13。

浮子段起始位置对脐带缆有效张力的影响见图14。从图14中可以看出，当浮子段起始位置变大时，悬挂段的长度变大，但浮子段提供的浮力未变，从而导致顶部悬挂点处的有效张力，也就是脐带缆的最大张力变大，见表4。而与之相反的，当浮子段起始位置变大后，脐带缆下降段的长度变短，导致下降段对浮子段的拉力变小，从而导致浮子段末尾处的有效张力变小。

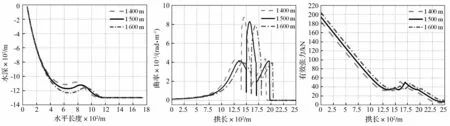
图12 浮子段不同起始位置下脐带缆初始线形Fig.12Configurationfordifferentstartinglocationsofthebuoyancycatenary图13 浮子段不同起始位置下脐带缆弯曲曲率Fig.13Curvaturefordifferentstartinglocationsofthebuoyancycatenary图14 浮子段不同起始位置下脐带缆有效张力Fig.14Effectivetensionfordifferentstartinglocationsofthebuoyancycatenary

表4　浮子段不同起始位置下的最大张力和曲率

3.4顶部悬挂角的参数敏感性分析

在保持其他参数不变的情况下，计算当顶部悬挂角为8°、10°和12°时脐带缆的静态响应，得到不同悬挂角下脐带缆的初始线形见图15。从图15可看出，顶部悬挂角决定着脐带缆顶部悬挂点与触地点之间的水平跨距。当顶部悬挂角增大时，脐带缆水平跨距增大，波形变缓，从而导致脐带缆的最大弯曲曲率变小，见图16和表5。在水平跨距为700～1000m处大致为脐带缆的浮子段区域，从图15可以看出，当悬挂角变大，脐带缆浮子段区域处的跨距也变大，波形变缓，从而导致浮子段上的曲率变小，见图16。

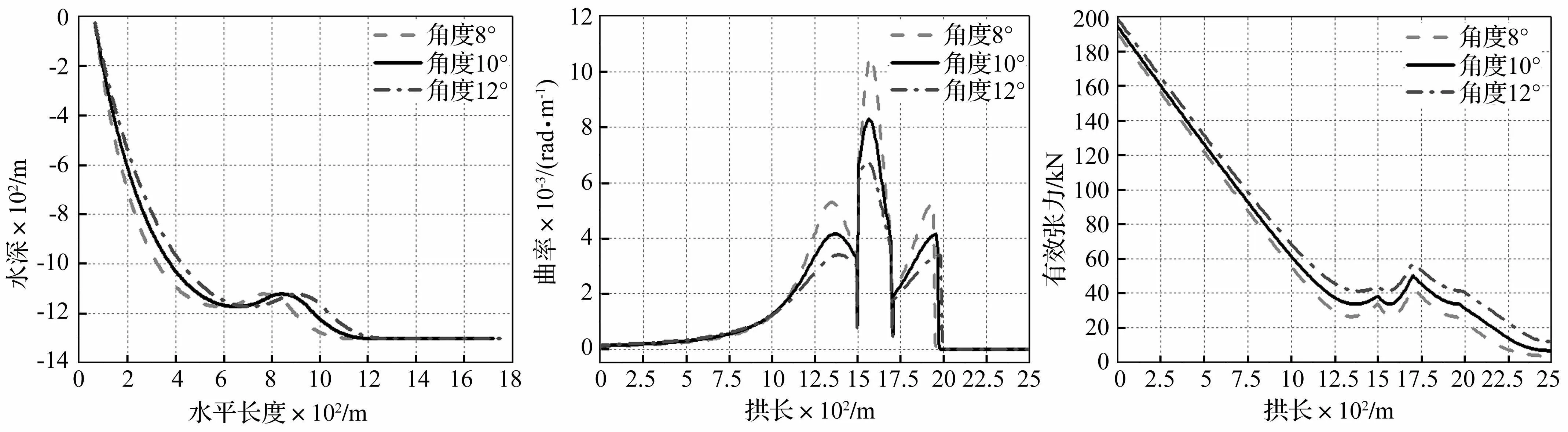
图15 不同顶部悬挂角下脐带缆初始线形Fig.15Configurationfordifferenttophang-offangles图16 不同顶部悬挂角下脐带缆弯曲曲率Fig.16Curvaturefordifferenttophang-offangles图17 不同顶部悬挂角下脐带缆有效张力Fig.17Effectivetensionfordifferenttophang-offangles

表5　不同顶部悬挂角下脐带缆最大张力和曲率

顶部悬挂角对脐带缆有效张力的影响见图17。从图中可以看出，沿着长度方向，整条脐带缆上的有效张力都随着悬挂角的增大而增大。从表5可看出，脐带缆上最大有效张力随着顶部悬挂角的增大而增大。

4结论

本文分析了脐带缆在缓波形布局下的整体结构响应性能，讨论了浮子段长度、浮力因子、浮子段起始位置以及顶部悬挂角对脐带缆结构响应的影响。本文的主要结论如下：

(1)缓波形布局下，脐带缆有效张力的极大值点为顶部悬挂点及浮子段末尾点，而张力最大值出现在顶部悬挂点；弯曲曲率的最大值点为浮子段上升举段的末尾点，而不是触地点，这与悬链线布局是不一致的。在缓波形布局下，脐带缆浮子段的曲率是否大于触地点曲率，可以通过浮力设计进行控制，尤其是对深水脐带缆的设计。

(2)浮子段长度与浮力因子对脐带缆结构响应的影响是类似的。增大浮子段长度或浮力因子会使脐带缆波形变陡，最大有效张力减小，最大弯曲曲率变大。浮子段上的弯曲曲率对浮力因子的变化很敏感，在设计中，应注意浮力因子的选取，防止因浮力过大导致浮子段上发生过大的弯曲。

(3)浮子段起始位置与顶部悬挂角对脐带缆结构响应的影响是类似的。增大浮子段起始位置或顶部悬挂角会使脐带缆波形变缓，最大有效张力增大，而最大弯曲曲率减小。

参考文献

[1]International standard 13628-5: Petroleum and natural gas industries-Design and operation of subsea production systems-Part 5: Subsea umbilicals [S]. 2002.

[2]Arnesen G, Dalane J I, Aramanadka S S B, et al. Integrated semi and Steel Catenary Risers (SCRs) in deep water and harsh environment conditions [C]//Offshore Technology Conference, Houston, Texas, U.S.A, 2006.

[3]Nolop N C, Wang H H, Kan W C, et al. Steel catenary risers and offloading system [C]//Offshore Technology Conference, Houston, Texas, U.S.A, May 2007.

[4]黄维平，李华军. 深水开发的新型立管系统-钢悬链线立管(SCR) [J]. 中国海洋大学学报, 2006, 36(5): 775-780.

HUANG Wei-ping, LI Hua-jun. A new type of deepwater riser in offshore oil&gas production: the Steel Catenary Riser, SCR [J]. Periodical of Ocean University of China, 2006, 36(5): 775-780.

[5]梁辉. 深水开发中的SCR立管系统[J]. 中国造船，2008,49(增刊2):80-84.

LIANG Hui.Steel Catenary Risers in Deepwater [J]. Shipbuilding of China, 2008,49(Sup2):80-84.

[6]Yue B, Walters D, Yu W W. Lazy wave SCR on turret moored FPSO [C]//2H Offshore Inc, Houston, TX, USA, ,2011:19-24.

[7]Yang He-zhen, LI Hua-jun. Sensitivity analysis of fatigue life prediction for deepwater steel lazy wave catenary risers [J]. Technological Sciences,2011.

[8]李清泉,杨和振.深海缓坡型脐带缆干涉分析研究[J].振动与冲击,2012,31(15):180-184.

LI Qing-quan, YANG He-zhen. Interference analysis for deepwater lazy-waveumbilical [J]. Journal of Vibration and Shock, 2012, 31(15):180-184.

[9]孙丽萍，周佳，王佳琦. 深水柔性立管缓波型布置及参数敏感性分析[J]. 中国海洋平台，2011,26(3):37-42.

SUN Li-ping, ZHOU Jia, WANG Jia-qi. Lazy wave configuration and parameter sensitivity analysis of deepwater flexible riser[J]. China Offshore Platform, 2011,26(3):37-42.

[10]API RP 2RD: Design of Risers for Floating Production Systems (FPSs) and Tension Leg Platforms (TLPs) [S]. American Petroleum Institute, Washington, DC, 1998.

[11]Li Song-cheng, Dynamic response of deepwater lazy-wave catenary riser[C]//2H Offshore Inc. & Chau Nguyen, 2H Offshore Inc.

[12]OrcaFlex Manual: Version 9.5a, UK, 2006.

第一作者上官文斌男，博士，教授，博士生导师，1963年生