铁道罐车流固耦合纵向冲击振动特性实验研究

铁道罐车流固耦合纵向冲击振动特性实验研究

张济民1,张琴1,周和超1,王开文2

(1.同济大学铁道与城市轨道交通研究院，上海201804; 2 西南交通大学牵引动力研究中心,成都610031)

摘要：考虑流固耦合作用下建立由铁道罐车组成的列车的纵向振动及冲击模型的方法仍然是该领域研究长期面临的挑战。为实现此目标，使用某原型车1∶5缩比简化的铁道罐车车辆进行实验，基于随机减量技术和Morlet小波变换方法来研究空载、不同装载高度及装载不同介质时罐车流固耦合模型的纵向冲击及振动特性。随机减量技术用于获得罐车系统的纵向自由响应信号，然后使用Morlet小波变换方法分析自由振动信号，从而辨识出系统的纵向振动频率及阻尼比。

关键词：铁道罐车；流固耦合；纵向冲击实验；Morlet小波变换

中图分类号:U272.4文献标志码：A

Tests for a railway tank car’s longitudinal vibration and impact characteristics considering fluid-structure interaction

ZHANGJi-min1,ZHANGQin1,ZHOUHe-chao1,WANGKai-wen2(1. Institute of Railway and Urban Mass Transit,Tongji University, Shanghai 201804, China; 2. Traction Power Research Center, Southwest Jiaotong University, Chengdu 610031, China)

Abstract:It faces long-term challenges to establish the longitudinal vibration and impact dynamic models of a train consisting of railway tankers considering fluid-structure interaction. In order to realize this goal, a railway tank car model was built with a scale ratio of 1∶5. The longitudinal impact and vibration characteristics of this model with different filling ratios of tanker and different types of rice were studied based on the method of random decrement technique (RDT) and Morlet wavelet transformation(WT). Morlet WT was applied to analyze free longitudinal responses of the railway tank car model while these free long itudinal vibration signals were obtained with the random decrement technique (RDT), thus the system’s longitudinal resonance frequencies and damping ratios were identified.

Key words:railway tank car; fluid-structure interaction; rail impact testing; Morlet wavelet transformation

通过公路运送高危险液体货物考虑流固耦合相互作用的汽车的方向动力学性能及稳定性特性已经受到广泛地关注和较深入的研究[1-2]；而在铁路系统，运输液态物品的罐车考虑流固耦合作用的动力学特性及纵向冲击振动特性的研究还很少，即使在某专向特性方面的尝试研究也非常少。Ursuljak等[3]研究了在制动模式下不同列车编组时装有液体货物列车的纵向动力学性能；Vera等[4]运用四个装满液体容器并把其视为多体系统并模拟流固耦合作用下的，包括流体晃动和等效液体力学模型。Tyrell等[5]运用实验进行了不同速度等级下冲击测试，以期确定在纵向冲击下主线发生事故可能的范围。还有其他一些研究者进行了流固耦合作用下的结构强度，包括冲击的动态响应。

虽然涉及列车脱轨事故已得到一定的研究，但从根本上找到这些事故的原因，尤其是列车中编组有装有流体的罐车时，一直难以实现。装运流体的罐车除自身是一个非常复杂的动态系统外，复杂的流体系统本身构成了子系统之一，罐车流固耦合系统振动的所有动态特性很难完整和准确的获得。同时，列车的载重和速度在最近几年都有很大程度上增加和提高，质量和速度的增加也增加了车辆和流体、轮轨之间以及列车车辆之间的相互作用，这种多重复杂的耦合作用最终将影响车辆或列车运行的安全性能。

为了解决直接影响到车辆结构强度和运行的列车运行安全的流固相互作用及耦合振动特性的认识及模型建立这一困境，设计了一个原型为G70罐车的1∶5比例的实验罐车，来研究装运流体铁道罐车复杂的动态特性。使用罐车进行了实验并对纵向流固耦合振动动态特性进行了研究。对实验采集的纵向振动信号运用随机减量方法(RDT)得到纵向流固耦合振动线性模型的响应，引入小波变换分析方法来计算分析不同装载工况下罐车的纵向振动特性，以期建立罐车纵向流固耦合振动的合理模型。

1实验及数据处理

1.1实验设计

大型工程结构的实物实验不仅要花费大量的人力、物力和时间，而且一定要先有实物，不能在实物产生以前预知其实验结果并为新方案结构的设计事先提出实验数据。为弥补这个不足，就需要进行模型实验，将其实验结果按一定的原理和方法再推算到实物上去，以此来了解实物的性能。模拟实验方法是以相似理论[6]为基础的，要使模型实验结果能运用到实物上来，就需要遵守相似理论的制约。力学相似理论是模拟研究的基础，要使实物与模型完全的力学相似，则它们必须是几何相似、物质相似以及运动相似，由此得出的长度、速度、加速度、作用力、振动频率、以及阻尼系数可通过相应的比例系数换算到实物模型。

根据相似理论设计了原型为G70罐车的1∶5比例实验罐车(图1)，并对此实验罐车进行纵向耦合冲击的实验研究。实验罐车具体结构：长度为2 700 mm的空心圆筒罐，罐体直径为600 mm，厚度为2 mm；罐车底架宽度为1 300 mm。为了获得罐车纵向加速度，加速度计沿纵向安装在构架前端靠近冲击端处，以采集纵向振动及冲击后的加速度。

图1　罐车模型 Fig.1 Therailway tanker model

实验轨道包括上平道，坡道和下平道，其中坡道斜率约为15%。上下平道分别为3 m、10 m，坡道长约10 m，坡度约15%。在下平道的末端设置一个装有弹簧的挡车装置，用于给行驶车辆提供减速缓冲，且可以通过更换不同刚度的弹簧来改变缓冲刚度。实验线路端部止挡弹簧刚度选为0.41 MN/m。如图2所示。

图2　线路模型 Fig.2 The line model

1.2实验数据采集

采用美国国家仪器公司(NI)的数据采集系统的SXCI平台进行实验数据的采集。纵向加速度传感器为AS-7GB，采样频率1 000 Hz的采样频率。按照罐体内装载容量的不同和装载介质的不同，分为空车、50%米、75%米、95%米、50%水、75%水、95%水共7个工况进行实验。为了得到准确的实验结果，每个工况进行多次实验，且同一工况的每次实验都将罐车推到斜坡的固定位置处(图2标记处)以期得到罐车一定的运行速度。当罐车空载、装载容量为75%大米以及75%水时，罐车系统纵向加速度时间历程如图3所示。

图3　空载与75%工况罐车加速度时间历程 Fig.3 Theacceleration signal of no-load and 75% filled

由图3可知，装水时罐车纵向振动幅度远大于装米及空载时的纵向振动，说明水的作用增大了罐体的纵向振动；空载时罐车纵向振动幅度大于罐车装大米工况，是由于罐车系统质量在空载时小于装大米工况。

为了研究基于流固耦合的罐车纵向特性，需要具有罐车系统的纵向自由振动响应信号，本文采用随机减量技术的方法分析加速度信号获得罐车自由振动响应信号。

1.3随机减量技术及实现

随机减量技术是一种利用随机激励下系统的响应信号构造一个系统的自由振荡信号的方法，在环境激励条件下，对一个线性系统来说，其自由响应信号可以定义为：

(1)

y为加速度响应，N代表触发点的数量，y(t)是样本的平均值，t为自由响应时间长度，ti是第i个触发点对应的时刻。

将随机减量技术应用于铁路罐车流固耦合纵向加速度信号的处理，可以得到空载罐车、装大米与装水罐车分别在装载容量50%、75%和95%工况下的冲击振动的自由衰减信号。图4表示空载及装载容量为75%时罐车纵向的自由振动响应历程。

图4　空载及装载高度为75%时罐车纵向的自由振动响应 Fig.4 The RD signal of no-load and 75% filled

2基于小波变换的罐车流固耦合纵向振动模态参数辨识

2.1小波变换

小波变换具有时域和频域的局部化特性，因而能够有效的从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析。相比于傅里叶变换，小波变换不仅能够在频域内对信号进行分析，也能在时域内对信号进行分析。与其他线性的时间-频率方法相比，小波变换的主要特征是保证了多分辨率：在高频时具有低分辨率，低频时具有高分辨率。在数学上，函数y(t)的连续小波变换为：

(2)

在频域内，

(3)

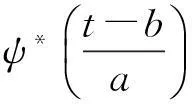
本文采用Morlet小波[8]：

ψ(t)=ejω0t e-t2/2

(4)

在频域表达为：

(5)

ω0是母波频率。当ω=ω0/a时，ψ(aω)取得最大值，此时Morlet小波可视为带宽与1/a或者中心频率ω0成正比的线性带通滤波器。

由于在某阶固有频率处小波变换系数将达到局部最大值，本文利用这一特性来辨识系统频率。当采用Morlet小波函数时，频率和扩张系数a之间的关系是fj=f0(fs/fω)(1/aj)，其中fs和fω是信号和小波的采样频率，f0是小波的中心频率。图5(a)～图5(e)为装75%水时实验罐车纵向振动频率的分析过程。

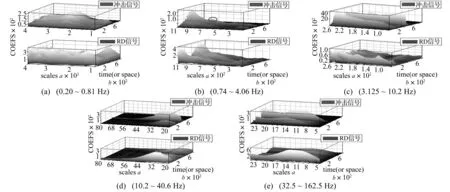
图5　装载75%水时小波变换图 Fig.5 The WT of 75% filled with water

图5(a)～(e)中，上下两图分别为冲击信号和随机减量(RD)信号的小波变换(WT)图，RD图是过滤掉冲击信号之后的WT图。图(a)上下两图都在a=3500(0.23 Hz)处有脊，RD图在a=1 500(0.54 Hz)处有较大的脊，这两个脊都由振动产生。图(b)中a=800(1.02Hz)处，上图有脊RD图没有脊，说明1.02 Hz处的脊是由冲击产生的，此处的局部放大图如图6所示。图(c)中上下两图的脊都很小，都是由振动产生的。图(d)a=32(25.4 Hz)处，上、下两图都有较大的脊，说明此处的脊由罐车本身振动产生。图(e)中a=14.2(57.2 Hz)处，上图有较大脊，RD图中没有脊，说明是由于冲击产生的脊；在a=13.4(60.6 Hz)及a=11(73 Hz)处RD图有较大脊，两处脊皆由振动产生。

图6　a=800(f=1.02 Hz)处局部放大图 Fig.6 The partial enlargement at a=800(f=1.02 Hz)

用同样的方法分析其他工况的冲击信号和RD信号，各工况各阶频率见表1至表4。对比表1至表4可以得出以下几个结论：第一，0.23 Hz、0.54 Hz、0.9 Hz和1.02 Hz是所有工况共有的频率，表示这四个频率是罐车本身固有的振动频率，不受装载介质与装载容量的影响，其中，罐车系统所有工况在1.02 Hz时都有冲击产生；第二，随着装载容量的增加，罐车系统的总质量增加，系统的振动频率和冲击频率逐渐减小。对比表2至表4，装大米工况与装水工况相同装载容量下，罐车装米时振动频率及冲击频率都远远小于罐车装水时相应的频率。

2.3基于小波变换的阻尼比辨识

本文实验用罐车具有强烈的非线性，难以定义其阻尼。为了获得系统的阻尼比系数，把系统视作线性。具有粘性阻尼的单自由度系统的脉冲响应是：

(6)

若认为系统是无阻尼的，则可以定义：

Α(t)=Y0e-ξωnt

(7)

φ(t)=ωdt+φ0

(8)

具有粘性阻尼的单自由度系统的脉冲响应信号y(t)的小波变换为:

按照贫困村退出标准，对各村的排水、道路、供电、供气、便民服务中心、警务室、村办公场所、幼儿园和活动广场等基础设施进行了完善。

式(9)的模表示为：

(10)

(11)

对等式(11)的两边求对数，则得到：

图7　载75%水时RD信号在57.2 Hz下小波的拟合线 Fig.7 The WT linear fitting of the RD signal when 75% filled with water

用小波变换方法分析罐车系统分别在空载、50%大米、75%大米、95%大米、50%水、75%水和95%水工况下的自由振动响应信号，得到所有这些工况的阻尼比列在表1至表4中。

表1　空车工况频率和阻尼比识别统计

表2　工况50%频率和阻尼比识别统计

表3　工况75%频率和阻尼比识别统计

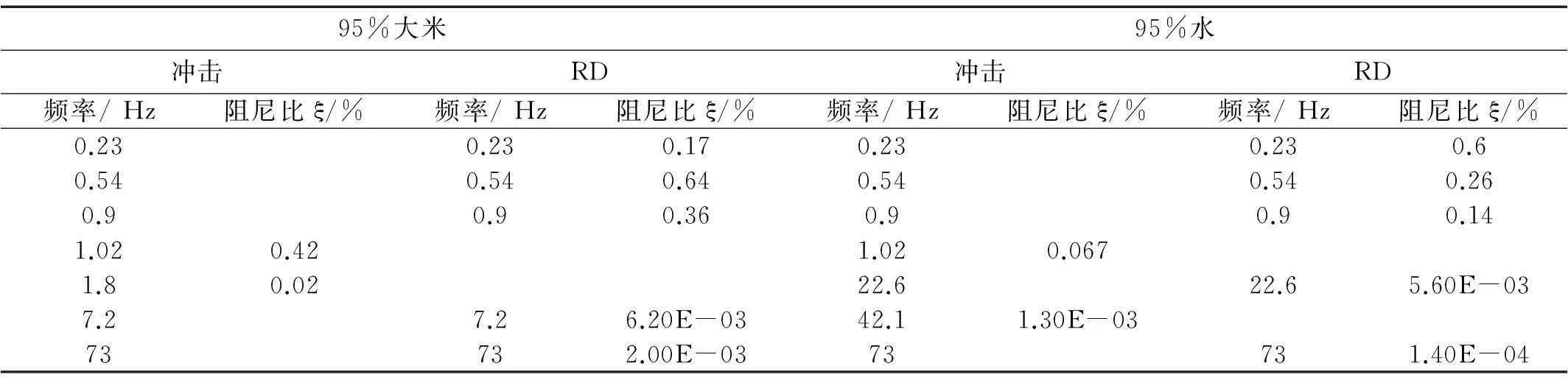
表4　工况95%频率和阻尼比识别统计

从表1至表4可以看出，在所有工况共有的低频区，包括0.23 Hz、0.54 Hz、0.9 Hz和1.02 Hz，装载条件不同导致不同工况在这些频率下的阻尼比不同；在所有工况条件下，罐车系统纵向振动频率处于中高频区域时阻尼比都很小，低频域的阻尼比要大于高频域时；罐车装米工况下冲击频率对应的阻尼比大于装水工况下相应阻尼比。

3结论

本文运用随机减量技术(RDT)从罐车系统原始冲击信号响应获得纵向自由振动响应，并应用Morlet 小波变换对该自由振动信号进行分析获得不同工况下模型振动频率及阻尼比。结论如下：

(1)从罐车系统不同工况下纵向振动加速度图可以得知，罐车装水时的纵向振动幅度远大于罐车装米及空载时的纵向振动，说明水的作用增大了罐体的纵向振动；空载时罐车纵向振动幅度大于罐车装大米工况，是由于罐车系统质量在空载时小于装大米工况。

(2)罐车系统的纵向振动频率随着载重质量的增加而逐渐减小。装大米工况与装水工况相同装载高度下，罐车装米时振动频率及冲击频率都远远小于罐车装水时相应的频率。

(3)在所有工况共有的低频区，包括0.23 Hz、0.54Hz、0.9 Hz和1.02 Hz，装载条件不同导致不同工况在这些频率下的阻尼比不同；罐车装米工况下冲击频率对应的阻尼比大于装水工况下相应阻尼比。

参考文献

[1]Ranganathan R, Rakheja S, Sankar S. Directional response of a B-Train vehicle combination carrying liquid cargo[J]. Journal of Dynamics System, Measurement and Control, 1993, 115.

[2]Rakheja S, Ranganathan R. Estimation of the rollover threshold of heavy vehicles carrying liquid cargo: a simplified approach[J]. International Journal of Heavy Vehicle Systems, 1990,1(1):79-98.

[3]Ursuljak L V, Romanjuk Y N. On the problem of dynamic response of the long trains including joint ones with the liquid cargo[J] Transbaltica,2011:269-274.

[4]Vera C, Paulin J, Suarez B, et al. Simulation of freight trains equipped with partially filled tank containers and related resonance phenomenon[C]// Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2005: 219-245.

[5]Tyrell D, Martinez E, Jeong D, et al. Improved Tank Car Safety Research[R]. RTDF2007-46013.

[6]王福天. 车辆系统动力学[M].北京：中国铁道出版社，1994.

[7]聂雪媛，丁桦. 基于随机减量技术的模态参数辨识方法探讨[J]. 机械设计学报，2012，29(8)：1-5.

NIE Xue-yuan, DING Hua. Discusstion of the Modal parameter identification method based on random decrement technique[J]. Journal of Machine Design, 2012, 29(8): 1-5.

[8]罗光坤，张令弥. 基于Morlet小波变换的模态参数识别研究[J]. 振动与冲击，2007，26(7)：135-138.

LUO Guang-kun, ZHANG Ling-mi. Modal parameter identification researches based on the Molet wavelet transform[J]. Journal of Vibration and Shock, 2007, 26(7): 135-138.