基于风洞试验的大跨度钢桁梁悬索桥颤振性能研究

基于风洞试验的大跨度钢桁梁悬索桥颤振性能研究

王凯， 廖海黎， 李明水

(西南交通大学风工程试验研究中心，成都610031)

摘要：目前研究大跨度桥梁颤振性能的主要手段是节段模型风洞试验，而如何利用试验结果对桥梁主梁断面进行优化还没有得到彻底解决。以某大跨度钢桁梁悬索桥为工程背景，给出了桥梁设计基准风速的计算方法和结果。进行1∶48比例节段模型颤振振动试验，得出了主梁在各个攻角下的颤振临界风速。在最不利工况下，试验了下中央稳定板、上中央稳定板和水平稳定板对主梁颤振性能的影响，最后根据试验结果，在考虑安全、经济和美观等因素的条件下，选择最优气动方案，满足了桥梁抗风设计的要求。最后用1∶100比例全桥气弹模型试验验证了节段模型试验结果的可靠性。同时总结了大跨钢桁梁悬索桥颤振折算风速值一般位于数值4左右的规律，为今后类似钢桁梁悬索桥的颤振性能研究提供了借鉴和参考。

关键词：钢桁梁；悬索桥；节段模型；颤振；气动优化；风洞试验

中图分类号:U441.3文献标志码：A

基金项目：国家自然科学

收稿日期：2014-10-13修改稿收到日期：2015-01-22

基金项目：国家安全重大基础研究项目(613157);国家自然科学基金重点项目(50939002);国家自然科学基金项目(51279038，51109042);黑龙江省四项基金资助项目(E201124)

收稿日期：2013-11-29修改稿收到日期：2014-05-20

Flutter performances of a long-span suspension bridge with steel trusses based on wind tunnel testing

WANGKai,LIAOHai-li,LIMing-shui(Research Center for Wind Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Abstract:Section model wind tunnel test is currently the main technique to investigate the flutter performance of long-span bridges. But a further study on applying test results in aerodynamic optimization of the bridges’ main beam is still needed. Here, the calculation methods and results for base wind speed of bridge design were presented with an example of one long-span steel truss girder suspension bridge. The flutter critical wind speeds at different attack angles were obtained through 1:48 proportion section model flutter tests. Under the most unfavorable working condition, tests to investigate the effects of upper central stabilized plate, lower central stabilized plate and horizontal stabilized plate on the flutter performance of the main beam were conducted. According to the test results, the optimal aerodynamic scheme was chosen to meet the requirements of the bridge wind resistance design in consideration of safety, economy and aesthetics. At last, the reliability of the results was verified with a 1:100 proportion full bridge aerodynamic elastic model test. The law that the flutter converted wind speed of long-span steel truss suspension bridges is approximately 4 was concluded as a reference for the investigation of the flutter performance of similar steel truss girder suspension bridges.

Key words:steel truss; suspension bridge; section model; flutter; aerodynamic optimization; wind tunnel testing

大跨度悬索桥由于其结构轻柔、阻尼较小，主梁自振频率低，对风的作用比较敏感，主梁的抗风安全性已成为大跨悬索桥设计中的重要考虑因素。特别是1940年美国Tacoma[1]大桥风毁事故，使得悬索桥的颤振稳定性研究得到大家广泛关注。1948年Bleich首次采用Theodor-son的平板气动自激力理论分析悬索桥颤振，1971年开始，Scanlan[1]长期致力于桥梁颤振稳定性研究，形成了一套风洞试验与理论分析相结合的方法。Ito等[2]采用概率分析方法研究了明石海峡大桥的颤振可靠性，明石海峡大桥针对桁架主梁断面采用了下中央稳定板与桥面开孔方案，提高了该桥的颤振稳定性。杨泳昕等[3]研究了西堠门大桥中央开槽箱型断面的颤振稳定性，分析了箱梁气动外形的改变及开槽宽度对悬索桥颤振稳定性的影响。陈政清等[4]对中央稳定板提高钢桁梁桥颤振稳定性的作用机理进行了详细研究，认为中央稳定板的作用机理是使颤振形态由单自由度向弯扭耦合颤振转移，从而提高了颤振临界风速。刘高等通过计算分析研究了采用主动控制翼板来抑制悬索桥的颤振。

桁架梁是大跨度悬索桥较常采用的一种断面形式，桁架断面具有抗扭刚度大、透风率高及方便在运输困难地区施工等优点，我国在山区峡谷地区修建了多座桁架悬索桥，如矮寨大桥、四渡河大桥、坝陵河大桥等。由于山地地形起伏影响，气流可能呈波浪状，自然风的非平稳特性将对桥梁结构产生非常不利影响，因此采取适当的措施确保桁架主梁断面颤振稳定性具有重要的工程实用价值。如矮寨大桥在钢桁梁中部设置下中央稳定板提高了该桥的气动稳定性。

本文以某山区大跨钢桁梁悬索桥为例，通过风参数计算、风洞试验等研究了上、下中央稳定板和水平导流板等不同措施组合对桁架悬索桥颤振稳定性的影响[5]，总结出了最优的颤振控制措施。

1工程概况

颤振性能试验基于某大跨度钢桁梁悬索桥进行，大桥跨越大峡谷，峡谷两岸地势陡峭，地形变化急剧，起伏很大，河谷深达几百米，桥位处为喀斯特地貌，桥位区气象条件为典型的山区峡谷风，桥梁主跨1130m，主梁为板-桁组合体系，宽27m、高7m，桥型布置如图1所示，主梁立面如图2所示。

图1 桥型布置 Fig.1 Arrangement of bridge

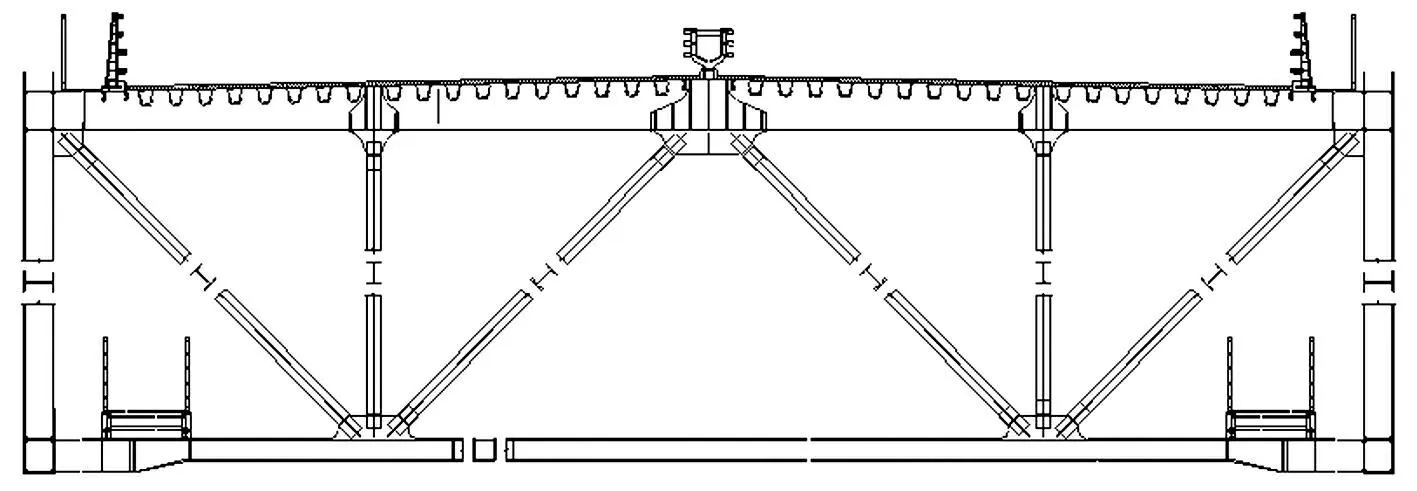
图2　主梁断面 Fig.2 Main girder cross section

2桥位风参数

桥梁桥址处为西南山区典型的峡谷地貌，桥梁两岸为悬崖峭壁，自然风经峡谷的狭管效应放大和缩小、反转和折回后，将产生众多涡旋，从而变得极为复杂。为了准确把握桥址处的实际风环境，根据从《公路桥梁抗风设计规范》中查出桥位200km范围内十个地区的最大风速和对应的百年风速，应用统计学中Gumbel Type Ⅰ极值分布计算得到桥位处基本风速[6]为29.40 m/s。

由于大桥位于山区峡谷，桥面高度处设计基准风速的确定还需要考虑山区峡谷的影响，即山区峡谷对基本风速的修正。假设大桥桥址处“虚拟”标准气象站的基本风速为峡谷进口风速，对于建于峡谷处的桥梁，可以借用以下经验关系式获得设计基准风速[7]：

(1)

式中：ud为建于峡谷上口处桥梁的设计基准风速；u10为桥位虚拟气象站的基本风速，即设为峡谷进口风速；H为峡谷深度，当桥梁建于峡谷上口处，可取桥面至峡谷下底面的高度；B1为峡谷上口处宽度，一般为桥梁桥面长度；B2为峡谷下底面宽度；κ为山谷效应修正系数。由式(1)计算出大桥设计基准风速见表1。

表1　设计风参数

3节段模型风洞试验

3.1静力试验

静力三分力系数是表征结构断面在平均风作用下受力大小的无量纲系数，它反映了风对桥梁的定常气动作用。目前随着理论发展和计算机技术进步，人们很多时候采用CFD技术计算某些断面的三分力系数，但是对于桁架主梁，计算结果往往与实际存在明显差距，因此对于桁架主梁，风洞试验仍然是必须的。风轴坐标系下的静力三分力系数按下式定义：

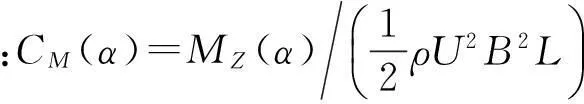
大桥主梁每个节间7.6m，考虑到模型每个桁架节间长度，模型采用1∶48几何缩尺比，模型弦杆采用优质木材制作，其余杆件、桥面防撞护栏、人行道护栏、检修轨道等均采用塑料板雕刻而成。图2为大桥钢桁架主梁断面。

试验在均匀流条件下进行，试验攻角为：α=-12°～+12°，Δα=1°，利用风速仪监测洞内风速。对大桥主梁标准梁段在成桥状态和施工状态时进行试验，测试风速为15 m/s，主梁成桥状态和施工状态的试验结果如图3和图4(体轴系)。

图3　成桥状态主梁断面三分力系数 Fig.3 Static force coefficients of completed bridge deck

图4　施工状态主梁断面三分力系数 Fig.4 Static force coefficients of bridge deck during erection

从图中可以看出，由于施工状态对比成桥状态，少了桥面铺装、栏杆、检修道等附属结构，主梁成桥状态和施工状态的三分力系数相差比较大，说明主梁成桥状态和施工状态的气动性能相差比较大。

3.2动力试验

针对钢桁架桥，动力试验主要检测主梁的颤振稳定性。颤振属于危险性的自激发散振动，当来流达到桥梁的颤振临界风速时，振动的桥梁通过气流的反馈作用不断从风中吸取能量，从而使振幅逐步增大，直至结构破坏。桥梁抗风设计要求桥梁的颤振临界风速必须高于相应的颤振检验风速。

试验是通过主梁动力节段模型风洞试验，直接测试主梁在不同攻角下发生颤振的临界风速，从而对该桥的动力抗风稳定性进行初步评估[8-9]，如果桥梁在颤振检验风速范围内出现发散性的颤振失稳，就必须进行气动措施优化。

试验在风洞实验室中进行，试验段设有专门进行桥梁节段模型动力试验的装置，模型由8根拉伸弹簧悬挂在支架上，形成可竖向运动和绕模型轴线转动的二自由度振动系统，试验支架置于洞壁外，以免干扰流场。为保证主梁断面气动绕流的二维特性，在主梁模型两端设置端板。在模型前方不干扰流场处设置风速仪，用来监控风洞内的风速。模型试验示意图如图5所示。

动力节段模型试验将桥梁的三维风致振动近似简化为弯扭耦合的二维振动问题处理。为考虑全桥的整体运动及不同方向振动间可能的耦合，试验时模型系统更精确的采用了计入全桥共同作用的等效质量和等效质量惯性矩。动力试验模型的试验参数见表2。

到目前为止，还没有一种被广泛接受用来估算桥梁结构阻尼比的方法。我国《公路桥梁抗风设计规范》中建议的桥梁结构阻尼比按下列取值：钢桥为0.5%、结合梁桥为1%、混凝土桥为2%。这些参考值主要针对主梁而言，桁架梁桥的主梁根据规范建议可以取为0.5%。为得到偏于安全的试验结果，在试验中偏安全地将模型系统的竖弯和扭转阻尼比均控制在0.5%水平以下。

考虑到断面的颤振临界风速对风攻角的敏感性，节段模型动力试验分别在0°、+3°、-3°三种攻角(来流风指向主梁下底面时为正攻角)情况下进行，试验均是在均匀流场中进行。颤振试验节段模型见图6。

试验是通过在模型下放置两个激光位移器，直接测量主梁节段模型的位移，同时观测发生颤振时对应的颤振临界风速，并通过风速比(模型试验风速与实桥自然风速之比)推算出实桥的颤振临界风速(由风致振动稳定状态转变为不稳定状态的临界点)。主梁的颤振风速见表3。

表2　节段模型主要试验参数

注：V—-竖向，T—扭转，S—对称，A—反对称，例：V-S-1表示第一对称竖弯。

表3　桥梁颤振临界风速

从表3中可以看出大桥主梁在-3°攻角下颤振临界风速高于颤振检验风速，主梁是安全的；但是在0°和+3°攻角下，颤振临界风速小于颤振检验风速，主梁的抗风设计不满足桥梁的设计要求，主梁断面需要进行一定的气动优化试验。

根据表3的结果，计算出桥梁的颤振折算风速，同时总结明石海峡大桥(主跨1991m钢桁梁悬索桥，世界第一跨径)、矮寨大桥(主跨1176m钢桁梁悬索桥)、抵母河大桥(主跨538m钢桁梁悬索桥)和清江大桥(主跨420m钢桁梁悬索桥)的颤振折算风速，将五座桥梁的颤振折算风速列于表4。

表4　桥梁颤振折算风速

从表4可以看出，大跨钢桁梁悬索桥的颤振折算风速基本位于数值4左右。清江大桥由于桥梁较窄，颤振折算风速稍微偏高。明石海峡大桥由于主跨较长，主梁扭转基频较低，并且主梁断面很宽，颤振折算风速也偏高。根据这个数值规律，可以大致推算大跨钢桁梁悬索桥的颤振临界风速，并对某些大跨钢桁梁悬索桥的颤振临界风速进行评价。

图5　模型试验示意图 Fig.5 Schematic diagram of model test

图6　安装在风洞中的节段模型 Fig.6 Section model installed at wind tunnel

4主梁气动优化试验

依据节段模型试验结果，大桥主梁在部分攻角范围内，颤振临界风速小于颤振检验风速。为了使大桥在山区特定条件下的颤振特性满足设计要求，避免因风致颤振引起的桥梁破坏事件发生，需要利用风洞试验对大桥主梁的气动外形进行一系列的风洞试验研究[10-12]。

试验中选择最不利攻角+3°进行优化试验，系统阻尼比设为0.5%，桥梁断面的优化方案(表5中的图圈出部分)及结果如表5(表中数据均换算到实桥)所示。

从表5可知，通过一系列节段优化试验，各方案对提高主梁的颤振发散风速都有一定作用，但是效果各不相同，结果如下：

(1)下中央稳定板对大桥主梁作用不明显，无论下稳定板多高，颤振临界风速都小于颤振检验风速；

(2)采用1.1m宽水平稳定板，颤振临界风速大于颤振检验风速，大桥颤振可以满足规范要求；

(3)上中央稳定板对颤振临界风速提高作用明显，当上稳定板与中央分隔带栏杆高度一样时，颤振临界风速略低于颤振检验风速；当上稳定板比中央分隔带栏杆高100mm或150mm时，主梁颤振稳定性都能很好满足抗风要求。

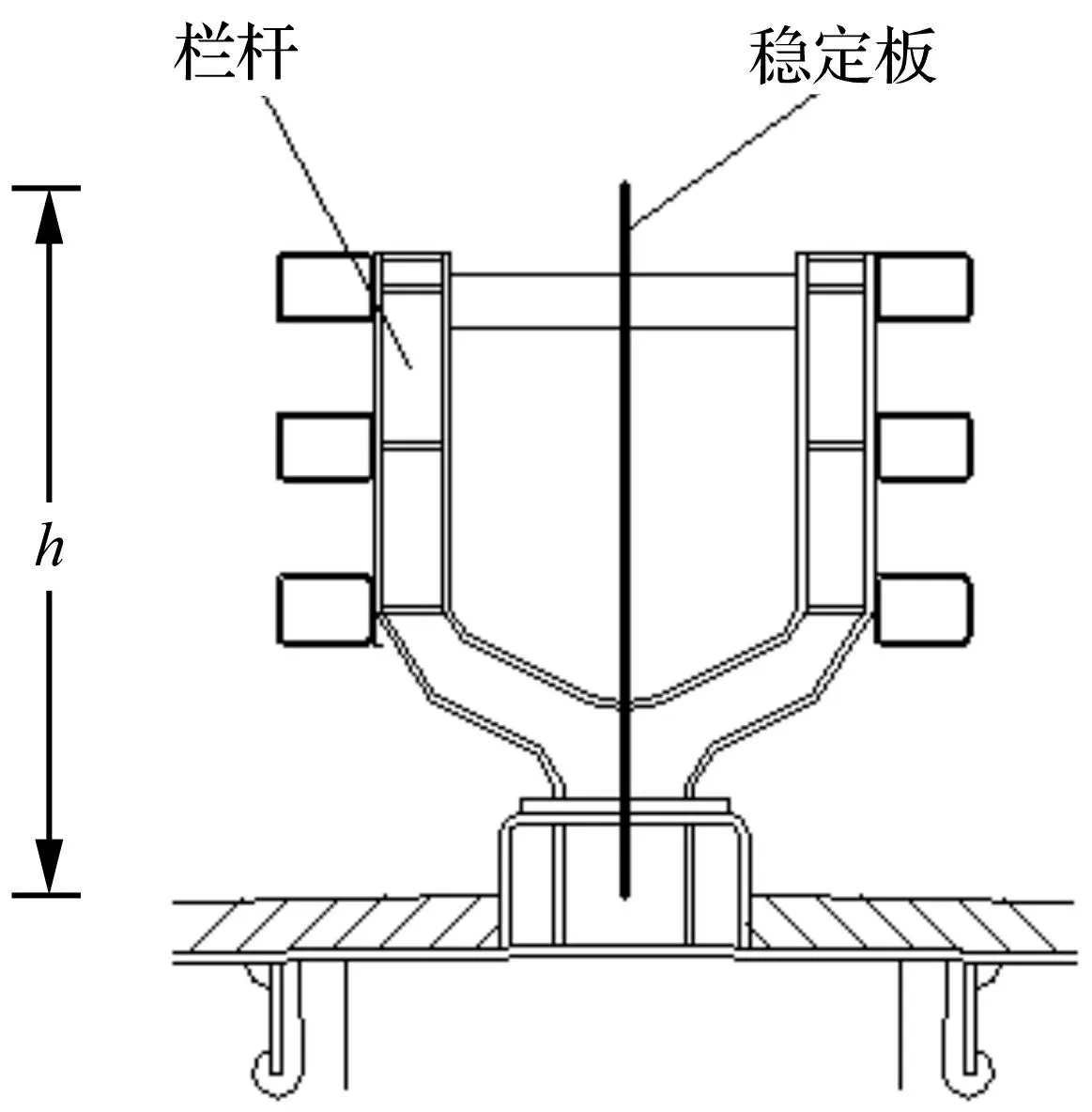
图7　稳定板断面布置图 Fig.7 Section arrangement of the central stability boards

综合以上分析，在不改变目前主梁断面的前提下，实际采用封住中央分隔带栏杆的措施，可以很好的改善主梁的抗风安全性。从主梁安全性和经济性两方面考虑，设置比栏杆高100mm的上中央稳定板是最优方案，见图7和图8。

表5　大桥主梁气动优化方案

图8　稳定板纵向布置图 Fig.8 Longitudinal arrangement of the central stability boards

5颤振性能的验证

全桥气动弹性模型能较真实地模拟结构的动力特性，较准确地反映结构与空气的动力相互作用，主要用于检验桥梁结构在均匀来流下的静风稳定、涡振、颤振、驰振等气动性能，以及在紊流条件下的抖振性能等。以全桥气弹模型试验进行节段模型颤振稳定性试验的验证[13]。

大桥设计阶段最终方案的确认是由西南交通大学XNJD-3风洞中的全桥气弹模型试验来进行的。XNJD-3风洞试验段长36m，宽22.5m，高4.5m，风洞空置时，风速范围为0～16.5 m/s，紊流度1.0%以下。该试验段可通过安装尖塔、锯齿板和粗糙元等装置模拟大气边界层。根据模型试验相似理论，并考虑桥位高度附近地形条件的模拟，设计制作了缩尺比1∶100的全桥气弹模型。全桥及桁架梁局部模型如图9、图10所示。

图9　全桥气弹模型 Fig.9 Full bridge aerodynamic elastic model

图10　主梁局部模型 Fig.10 Section girder model

全桥气弹模型风洞试验测试了均匀流及紊流场中-3°、0°、+3°三种风攻角下的颤振临界风速，紊流和均匀流场中均未观测到颤振失稳现象。表6为全桥气弹模型无中央稳定板和设置中央稳定板的颤振临界风速对比结果。

表6　全桥气动弹性模型颤振临界风速对比试验结果

从表6中可知，大桥成桥状态，在0°和-3°攻角下，颤振临界风速大于颤振检验风速；在+3°攻角下，颤振临界风速小于颤振检验风速，不满足抗风设计要求。

通过设置比栏杆高100mm的上中央稳定板，大桥在成桥状态0°、-3°和+3°风攻角下颤振临界风速均大于颤振检验风速，满足抗风设计要求。

由于节段模型试验时一般为单模态振动，而全桥气弹模型试验，有多个模态参与主梁的振动，全桥气弹模型试验结果一般都大于节段模型试验结果，全桥气弹模型试验结果也验证了节段模型试验结果的准确性。

6结论

通过节段模型风洞试验、气动优化风洞试验及全桥气弹模型风洞试验对结果的验证，可得到以下主要结论：

(1)当桥位周围缺少气象资料时，可以通过附近国家气象站的资料，通过数学统计方法、山区地形修正，计算得到桥梁设计基准风速。

(2)对于大跨度钢桁梁悬索桥，运用合适的气动优化措施，一定能解决桁架梁的颤振稳定性问题。

(3)大跨钢桁梁悬索桥颤振折算风速值一般位于数值4左右。

(4)下中央稳定板对于板-桁组合式桁架梁桥的颤振临界风速的提高作用不明显。

(5)上中央稳定板和水平稳定板对板-桁组合式桁架梁桥，都能很明显的提高颤振临界风速。

(6)上中央稳定板、下中央稳定板和水平稳定板安装的高(宽)度等对颤振发散风速影响较大，需通过试验确定稳定板安装的位置、高(宽)度和是否通长设置等参数。

因此，在对大跨钢桁梁悬索桥进行颤振性能评价时，需要结合试验，考虑阻尼、频率等一些因素，对主梁断面进行综合评价，选择最优断面形式。

参考文献

[1]Scanlan R H. Problematics in formulation of wind-force models for bridge decks[J]. Journal of Engineering Mechanics, ASCE, 1993, 119(7):1433-1446.

[2]Ito M, Fujino Y. A probabilistic study of torsion flutter of suspension bridge under fluctuating wind[C]// Proceedings of the 4th International Conference on Structural Safety and Reliability. New York: ASCE, 1985:145-160.

[3]杨泳昕, 葛耀君, 曹丰产. 大跨度悬索桥中央开槽箱梁断面的颤振性能[J]. 中国公路学报, 2007, 20(3):35-40.

YANG Yong-xin, GE Yao-jun, CAO Feng-chan. Flutter performance of central-slotted box girder section for long-span suspension bridges[J]. China Journal of Highway and Transport, 2007,20(3):35-40.

[4]陈政清, 欧阳克俭, 牛华伟, 等. 中央稳定板提高桁架梁悬索桥颤振稳定性的气动机理[J]. 中国公路学报, 2009, 22(6):53-59.

CHEN Zheng-qing, OUYANG Ke-jian, NIU Hua-wei, et al. Aerodynamic mechanism of improvement of flutter stability of truss-girder suspension bridge using central stabilizer[J]. China Journal of Highway and Transport, 2009, 22(6):53-59.

[5]中华人民共和国交通部. JTG/T D60-01-2004 公路桥梁抗风设计规范[S].北京:中国交通出版社,2004.

[6]王凯, 廖海黎, 李明水. 山区峡谷桥梁设计基准风速的确定方法[J]. 西南交通大学学报,2013,48(1): 29-36.

WANG Kai, LIAO Hai-li, LI Ming-shui. Determination method for basic design wind speed of mountainous valley bridge[J]. Journal ofSouthwest Jiaotong University, 2013, 48(1): 29-36.

[7]徐洪涛.山区峡谷风特性参数及大跨度桁梁桥风致振动研究[D]. 成都：西南交通大学,2009.

[8]徐洪涛, 廖海黎, 李明水. 坝陵河大桥节段模型风洞试验研究[J]. 世界桥梁, 2009(4): 83-89.

XU Hong-tao, LIAO Hai-li, LI Ming-shui. Wind tunnel test study of sectional model of baling river bridge[J]. World Bridges, 2009(4): 83-89.

[9]许福友, 陈艾荣, 张哲. 确定桥梁模型颤振临界风速的实用方法[J]. 振动与冲击, 2008, 27(12) : 97-102.

XU Fu-you, CHEN Ai-rong, ZHANG Zhe. Practical technique for determining critical flutter wind speed of bridge model[J]. Journal of Vibration and Shock, 2008, 27(12): 97-102.

[10]胡峰强. 山区风特性参数及钢桁架悬索桥颤振稳定性研究[D]. 上海：同济大学, 2006.

[11]刘慕广, 陈政清. 典型钝体断面大攻角下的颤振自激力特性[J]. 振动与冲击, 2013,32(10):22-25.

LIU Mu-guang, CHEN Zheng-qing. Characteristcs of self-excited forces in flutter of typical blunt body under large attack angles[J]. Journal of Vibration and Shcok, 2013,32(10):22-25.

[12]李春光, 张志田, 陈政清, 等. 桁架加劲梁悬索桥气动稳定措施试验研究[J]. 振动与冲击, 2008,27(9):40-43.

LI Chun-guang, ZHANG Zhi-tian, CHEN Zheng-qing, et al. Experimental study on the aerodynamic stability measure of a suspension bridge with truss stiffening girder[J]. Journal of Vibration and Shock, 2008,27(9):40-43.

[13]Zhu L D, Wang M, Wang D L. Flutter and buffeting performances of third Nanjing bridge over Yangtze river under yaw wind via aeroelastic model test [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007,95(9/10/11): 1579-1606.

第一作者朱喜锋男，博士生，讲师，1980年生

通信作者罗冠炜男，教授，博士生导师，1963年生

邮箱: luogw@mail.lzjtu.cn

第一作者王军男，博士生，1989年生

通信作者郭君男，博士，副教授，1981年生