剪式齿轮传动机构非线性动力学特性研究

剪式齿轮传动机构非线性动力学特性研究

何文运，张俊红，马梁

(天津大学内燃机燃烧学国家重点实验室，天津300072)

摘要：考虑齿侧间隙、时变啮合刚度和摩擦力等因素，建立7自由度剪式齿轮传动系统非线性动力学模型，采用Runge-Kutta法对转速、啮合齿隙、扭簧刚度、预紧力矩等对系统振动特性的影响进行了研究。结果表明，随着转速的升高系统逐渐进入混沌状态，中等转速区间系统的非线性动力学行为对转速的变化更为敏感；随着齿侧间隙的增大，混沌区间增大，混沌特性加强；扭簧刚度影响系统的非线性运动状态，但对冲击现象的影响较小，较小的扭簧刚度更有利于消除冲击现象；扭簧的预紧力矩影响系统啮合状态，最小预紧力矩的大小受负载力矩的影响且近似呈正比例关系。

关键词：剪式齿轮；非线性动力学；扭簧刚度；预紧力矩

中图分类号:TH132.41文献标志码：A

基金项目：南京总参创新工作站(NJCX-RW-20120226)

收稿日期：2014-02-12修改稿收到日期：2014-05-15

基金项目：国防基础科研计划(A2620110003,A2620130003)

收稿日期：2013-10-09修改稿收到日期：2014-07-12

Nonlinear dynamic characteristics of a scissor gear transmission system

HEWen-yun,ZHANGJun-hong,MALiang(State key Laboratory of Engines，Tianjin University，Tianjin 300072, China)

Abstract:Considering backlash of gear pairs, time-varying mesh stiffness and friction, a nonlinear dynamic model of a scissor gear transmission system with 7-DOF was established with the analytical mechanics theory. An example of such a system was used to investigate the effects of rotational speed, backlash, stiffness and preload of torsional spring on the nonlinear dynamic behavior of the system with Runge-Kutta method. The results showed that the system enters a chaotic state with increase in rotating speed, the nonlinear dynamic behavior of the system in the medium rotating speed range is more sensitive to the change of rotating speed; the larger the backlash, the bigger the rotating speed interval of chaos, the stronger the chaotic characteristics; the torsional stiffness of spring has an effect on the non-linear dynamic behavior of the system, but it has a smaller effect on the impact phenomenon, the smaller torsional stiffness is more helpful to avoiding separating and impacting states of the gear pair; preload of torsional spring affects meshing states of the system, the minimum preload torque is almost proportional to the effect of the load torque.

Key words:scissor gear; nonlinear dynamics; torsional stiffness of spring; preload of torsional spring

剪式齿轮可以及时动态弥补齿侧间隙，缓解齿轮啮合时的冲击，既降低了齿啮合的撞击噪声，又对所驱动附件的噪声有较大影响，从而在汽车行业噪声控制上得到广泛应用。国内外学者对剪式消隙齿轮机构的应用、设计、计算等方面进行了大量的研究取得了许多研究成果[1-4]，但对剪式齿轮传动系统非线性动力学方面的研究却较少。Kwon等[5]用三段柔性连接曲线表示消隙齿轮刚度模型，建立了消隙齿轮伺服机构动力学模型；Allan等[6]提出了一种计算消隙弹簧最小预紧力矩的方法，建立了不考虑时变啮合刚度的多刚体系统扭转运动学方程。杨政等[7-8]分析了齿轮参数变化对消隙齿轮综合啮合刚度的影响，建立了纯扭转动力学运动方程，分析了摩擦对消隙机构的影响。剪式齿轮消隙机构在工作时表现出复杂的非线性特性，对剪式齿轮的齿面接触特性、工作状态及传动系统的振动噪声会产生很大影响。本文考虑摩擦、齿侧间隙、时变啮合刚度、传动误差等因素，建立了7自由度剪式齿轮传动系统非线性动力学模型，采用数值计算方法对啮合齿隙、扭簧刚度、预紧力矩、转速等对系统振动特性的影响进行了研究，为剪式齿轮传动机构的优化设计提供参考与依据。

1非线性动力学模型

剪式齿轮，如图1所示，又称双片齿轮、消隙齿轮等，由固定齿轮Z2、浮动齿轮Z3和扭转弹簧组成。固定齿轮与传动轴固连，浮动齿轮空套在固定齿轮上，双片齿轮之间用加载的扭簧连接。当双片齿轮与配对齿轮啮合时，扭簧将迫使浮动齿轮相对于固定齿轮作微量转动，从而可有效消除齿轮本身误差引起的齿隙。但剪式齿轮不能完全消除轴承以及其它因素引起的齿隙，仍存在少量的残余回差[1]。

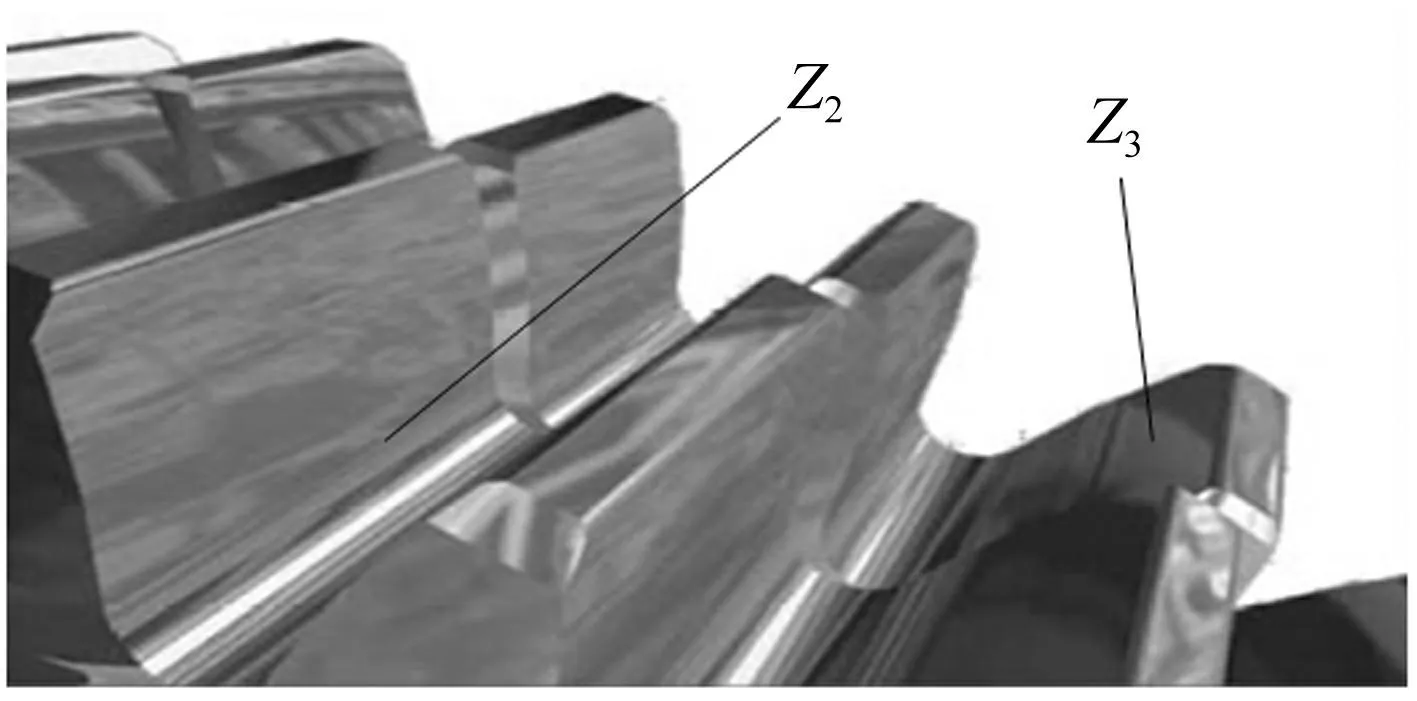
图1　剪式齿轮结构 Fig.1 Structure of scissor gear

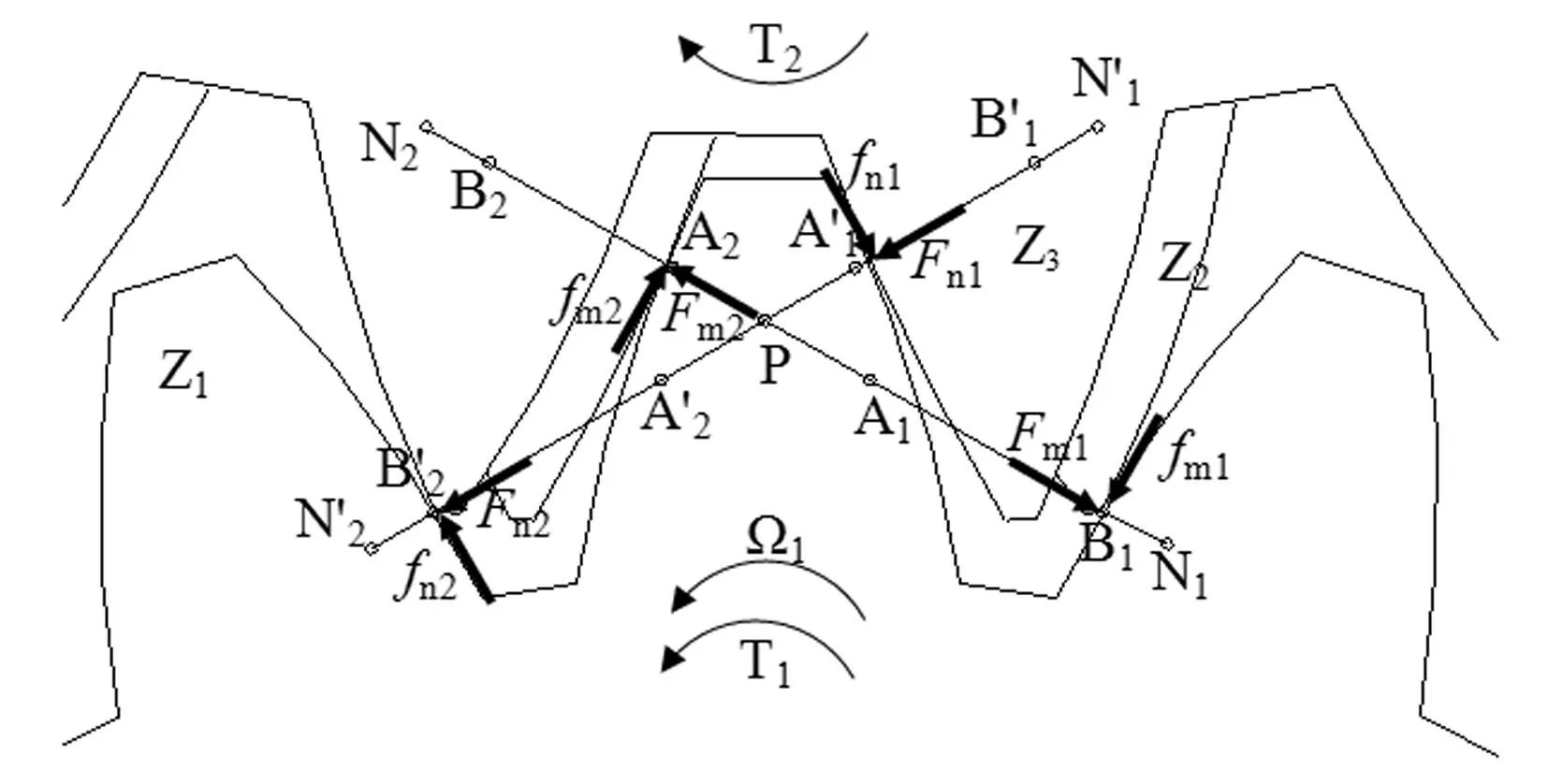
图2　剪式齿轮传动机构啮合过程分析 Fig.2 Meshing states of scissor gear transmission

建立剪式齿轮机构7自由度平移-扭转动力学模型如图3所示。该模型是一个集中参数模型，齿轮采用集中质量和集中转动惯量模拟，且系统对轴向误差不敏感，每个构件都在垂直于轴线的平面内振动；轴采用无质量的刚体模拟，轴承为弹性支撑；剪式齿轮组(齿轮2、3)同心配置，能彼此相对旋转，但没有相对平移。

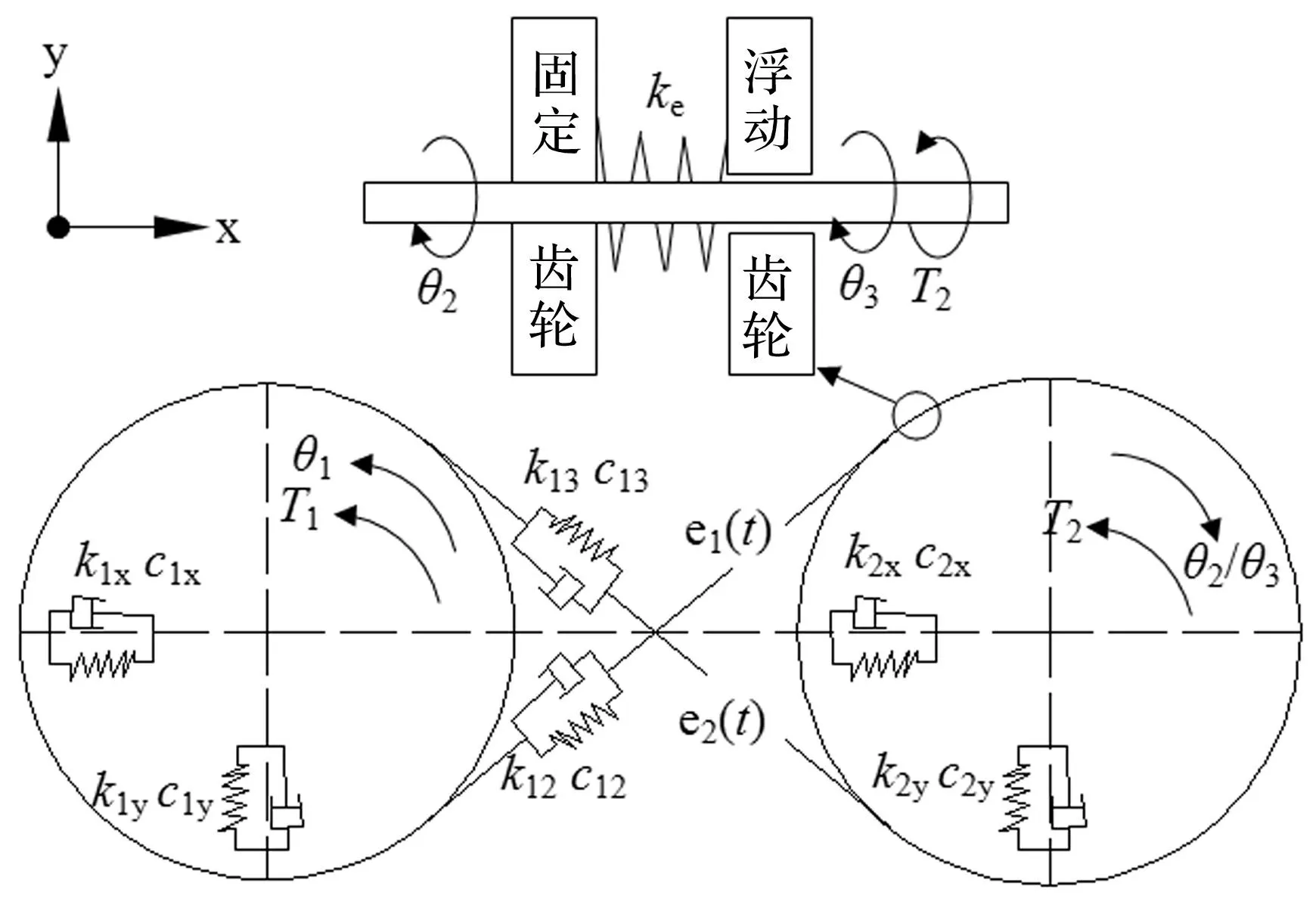
图3　剪式齿轮传动机构动力学模型 Fig.3 Dynamic model of scissor gear transmission

图3中cij、kij(i=1,2；j=x,y)为轴承的阻尼、刚度；ke为扭簧扭转刚度；c1i、k1i(i=2,3)为齿轮啮合的阻尼、刚度；θi(i=1,2,3)为各齿轮的扭转角。ei(t)(i=1,2)为齿轮副的法向静态传递误差，

式中，Aiel为误差的l阶谐波幅值；Ωe为齿轮副啮合频率；Φiel为l阶谐波相位。

该模型的非线性振动微分方程如下：

2时变啮合力及摩擦力分析

在齿轮系统中，时变刚度、时变摩擦和轮齿间隙及其之间的非线性强耦合使传动系统表现出复杂的非线性特性，是齿轮系统中最重要的内部激励。

由Ishikawa公式[9]可得单个啮合齿轮受啮合力作用时接触线上单位宽度的刚度ki(t)，

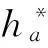
令齿轮副Z1-Z2的轮齿对1第一次在B1点啮入时为初始时刻t=0，由渐开线齿轮特性和啮合原理可知，齿轮副Z1-Z2轮齿对1与轮齿对2、齿轮副Z1-Z3轮齿对3与轮齿对4的瞬时啮合刚度如下式：

km1=k(mod(Ω1t,θ0))

kn1=k(mod(Ω1t+θ2-3,θ0))

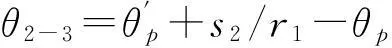
两齿轮齿面啮合点间由于振动和误差而产生的沿啮合点法线方向的相对位移为：

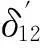
结合齿侧间隙位移函数g(δ′)可以求出啮合弹性力与阻尼力，其合力即为轮齿间的时变啮合力Fi(t)，

式中，cai为啮合阻尼，ki(t)为时变啮合刚度。啮合刚度是随啮合位置作周期性变化的时间函数，对其进行Fourier级数展开，以谐波形式拟合ki(t)，

式中，kai为时变啮合刚度的平均值；Aikl为时变啮合刚度的l阶谐波幅值；Ωh为齿轮副啮合频率；Φikl为l阶谐波相位。

齿轮副在连续运转的过程中，齿面摩擦力的大小和方向都发生周期性的变化，定义λ(t)为摩擦力方向系数，μ(t)为齿面摩擦系数，则齿面摩擦力fi(t)可以表示为：

fi(t)=λ(t)μ(t)Fi(t)(i=m1,m2,n1,n2)

式中，齿对Z1-Z2、Z1-Z3的摩擦力方向系数为：

润滑处于混合润滑状态时，齿面摩擦系数μ(t)适用Benedict & Kelly模型[10]，

式中，Savg为齿面间平均粗糙度；η为润滑油动力粘度；ξs为啮合点处滑移速度；ξe为啮合点处卷汲速度。

3动力学方程的无量纲化

式中，

a1=sinα，a2=cosα

ξij=cij/2miωn,(i=1,2;j=x,y)

ξνij=cij/2mνωn,(ν=1,2,e1,e2,e3;i=m,n;j=1,2)

φAmi=a1+λmiμmia2，φAni=a1+λniμnia2

φBmi=a2-λmiμmia1，φBni=a2-λniμnia1

4计算与讨论

以一压力角17.5°、模数2.25的剪式齿轮机构为研究对象，采用四阶Runge-Kutta方法对非线性微分方程进行求解，通过时间序列、相图、分岔图、Poincare截面、频谱及Lyapunov指数等方法对求解结果进行分析，研究系统参数对非线性动力学行为的影响。各齿轮参数如表1所示，各齿轮材料均为20CrMnTi。

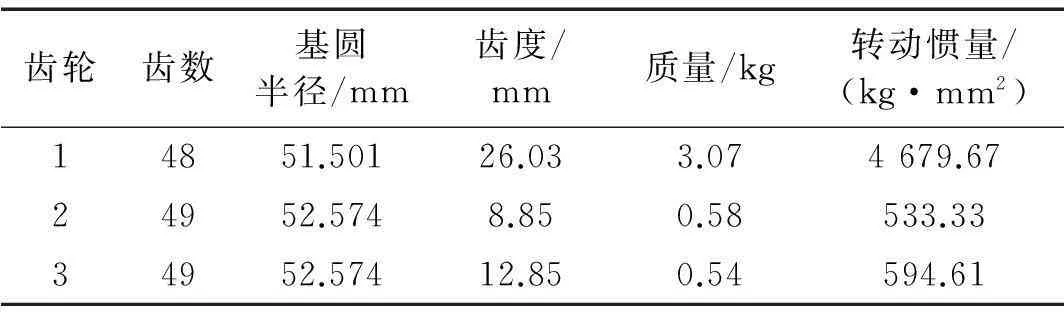
表1　传动机构各齿轮基本参数

齿轮的啮合阻尼可由下式计算[11]：

式中，ξg为齿轮啮合的阻尼比，一般为0.03～0.17，取ξg=0.09。各轴承的支撑刚度、阻尼取相同值，分别为：刚度Ks=5×108N/m，阻尼Cs=1 000 N·s/m。扭簧扭转刚度Ke=5×104N·m/rad。图4所示为只有主动齿轮Z1和固定齿轮Z2时的普通齿轮机构与剪式齿轮机构综合啮合刚度[7]对比曲线，可以看出剪式齿轮传动时的综合啮合刚度大于普通齿轮机构。

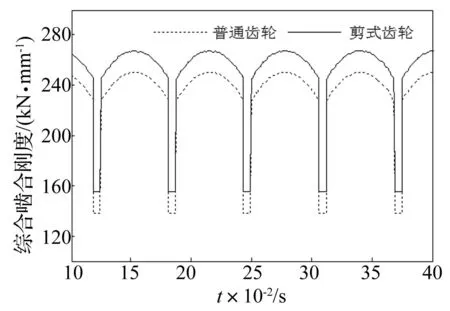
图4　剪式齿轮与普通齿轮综合啮合刚度对比曲线 Fig.4 Mesh stiffness of scissor gear comparing with normal gear

4.1齿侧间隙的影响

转速2 500 r/min、齿侧间隙20 μm时齿对Z1-Z2、Z1-Z3沿啮合线方向的无量纲相对位移δ1、δ2的时间历程、相图、Poincare截面、频谱如图5所示。由图5可知δ1、δ2均既存在大于一半齿隙又存在小于一半齿隙的现象，说明齿对Z1-Z2、Z1-Z3均处于单边冲击状态；相图为非椭圆闭合曲线，Poincare截面包含单一离散点，FFT频谱图的谱线为八个基频成倍数关系的离散分量，表明齿对Z1-Z2、Z1-Z3的响应为非简谐单周期响应。

图5　转速2 500 r/min、齿隙20 μm的响应 Fig.5 Responses at 2 500 r/min and backlash of 20 μm

转速2 500 r/min、齿侧间隙40 μm时δ1、δ2的时间历程、相图、Poincare截面、频谱如图6所示。由图6可知，齿对Z1-Z2、Z1-Z3均出现冲击，相平面图由相互缠绕和交叉但不重复不封闭的曲线组成，Poincare映射图为分布在一定区域的点集，FFT频谱图的谱线变为连续谱。以互信息法和G-P法确定时延和嵌入维，采用wolf法[12]计算得到的最大Lyapunov指数分别为0.000 333 63和0.001 455 1，均大于0，表明传动系统呈现混沌运动。

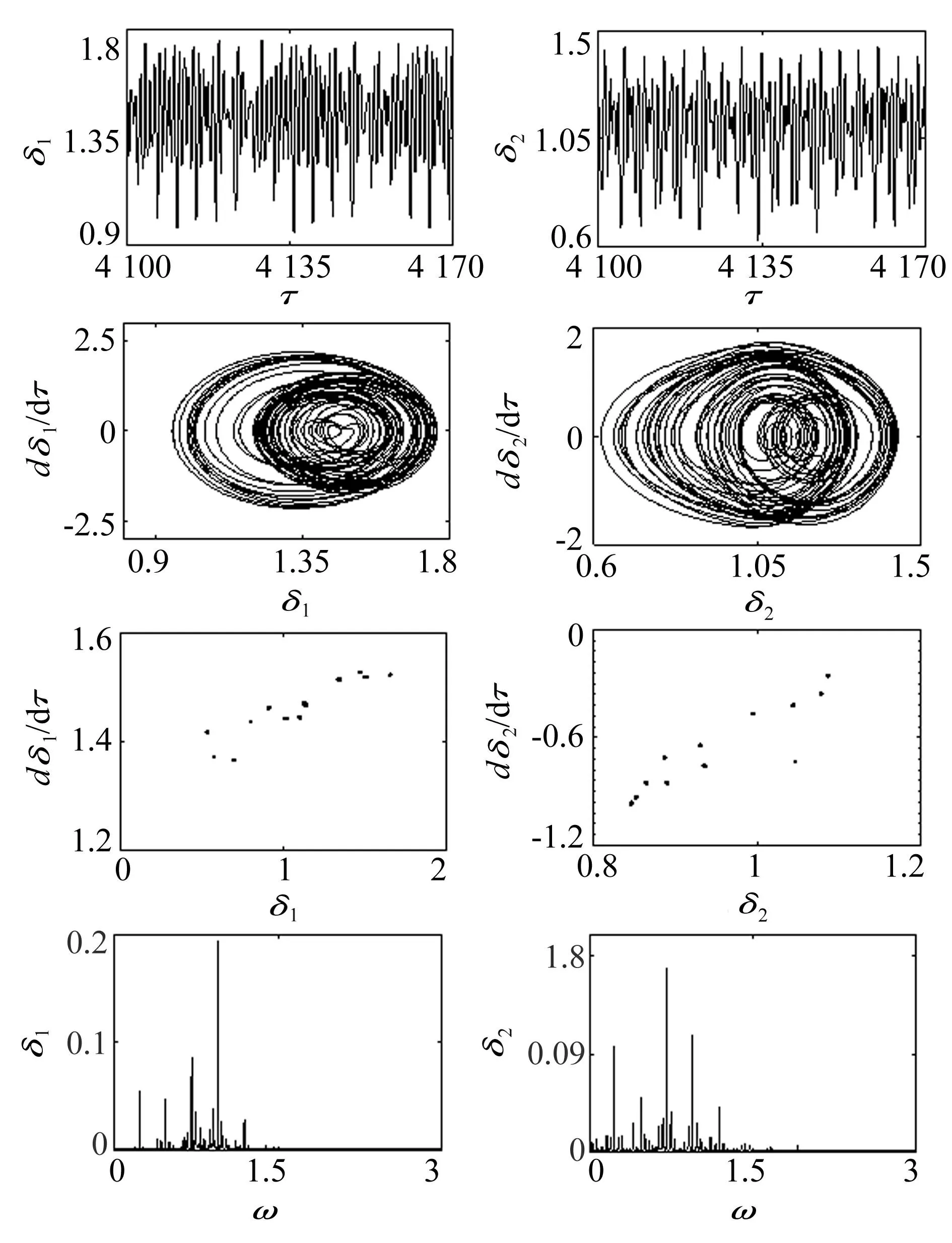
图6　转速2 500 r/min、齿隙40 μm的响应 Fig.6 Responses at 2 500 r/min and backlash of 40 μm

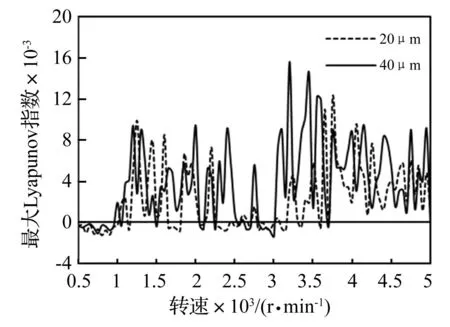
图7　最大Lyapunov指数与转速的关系 Fig.7 Variation of maximal lyapunov exponent with speed

图7所示为不同齿侧间隙时计算得到的齿对Z1-Z2、振动的最大Lyapunov指数随转速的变化。由图7可知，转速的变化对混沌的产生具有很大的影响。随转速的升高，最大Lyapunov指数由负值变为正值，即随着转速的升高系统逐渐进入混沌状态；且在中等转速时，混沌区域存在小于零的最大Lyapunov指数，说明在混沌参数区域存在周期窗口，在中等转速区间系统的非线性动力学行为对转速的变化更为敏感。同时可以看出，随着齿侧间隙的增大，混沌区间增大，混沌特性加强。

4.2扭簧刚度的影响

齿侧间隙取为20 μm，对扭簧刚度的影响进行分析。在其它参数不变的情况下，分别取转速为1 000 r/min、2 500 r/min，分析扭簧刚度在1.0×104～1.0×105N·m·rad-1区间变化时对传动系统动力学特性的影响。

转速1 000 r/min随扭簧刚度变化的分岔图和不同扭簧刚度时δ2的极大值与极小值如图8、图9所示。可以看出，随扭簧刚度的变化，系统出现了跳跃、分岔、混沌等非线性动力学特征，混沌与周期交替出现。在整个区间内，系统一直呈现冲击状态。当扭簧刚度在1.0×104～2.6×104N·m·rad-1之间时，冲击幅度基本保持不变，之后随着扭簧刚度的增加系统进入混沌运动状态，冲击幅度总体呈增大趋势；当扭簧刚度大于8.3×104N·m·rad-1时，系统退化为周期运动，冲击幅度略微减小。

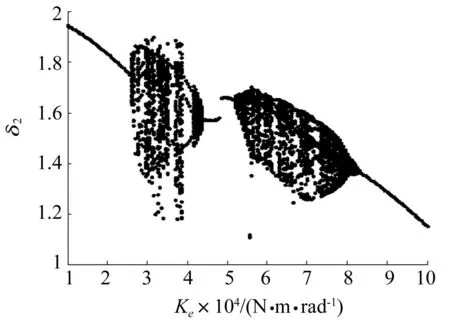
图8　转速1 000 r/min随扭簧刚度变化的分岔曲线 Fig.8 The bifurcation diagram depend on torsional stiffness of spring at 1 000 r/min

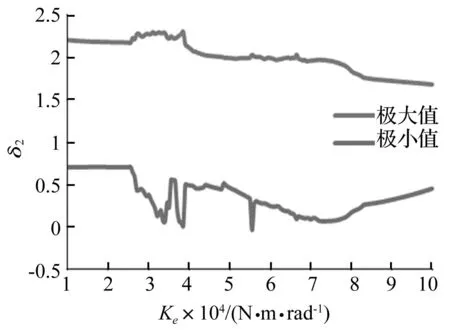
图9　转速1 000 r/min动态响应与扭簧刚度的关系 Fig.9 Relation between responses δ 2 and torsional stiffness of spring at 1 000 r/min

转速为2 500 r/min系统随扭簧刚度变化的分岔图如图10所示，不同扭簧刚度下沿啮合线方向的无量纲相对位移δ2的极大值与极小值如图11所示。可以看出，当扭簧刚度在1×104～3.2×104N·m·rad-1之间时，系统运动以周期运动为主，此区间内，冲击幅度基本保持不变，之后系统进入混沌运动状态，冲击幅度随扭簧刚度的增加变化明显；在4.9×104～5.0×104N·m·rad-1之间出现了短暂的周期运动，马上经倍周期分岔进入到混沌运动；在6.7×104N·m·rad-1附近冲击幅值发生跳跃；当扭簧刚度大于9.4×104N·m·rad-1时系统由混沌运动经2倍周期分岔退化为周期运动，冲击幅度减小。

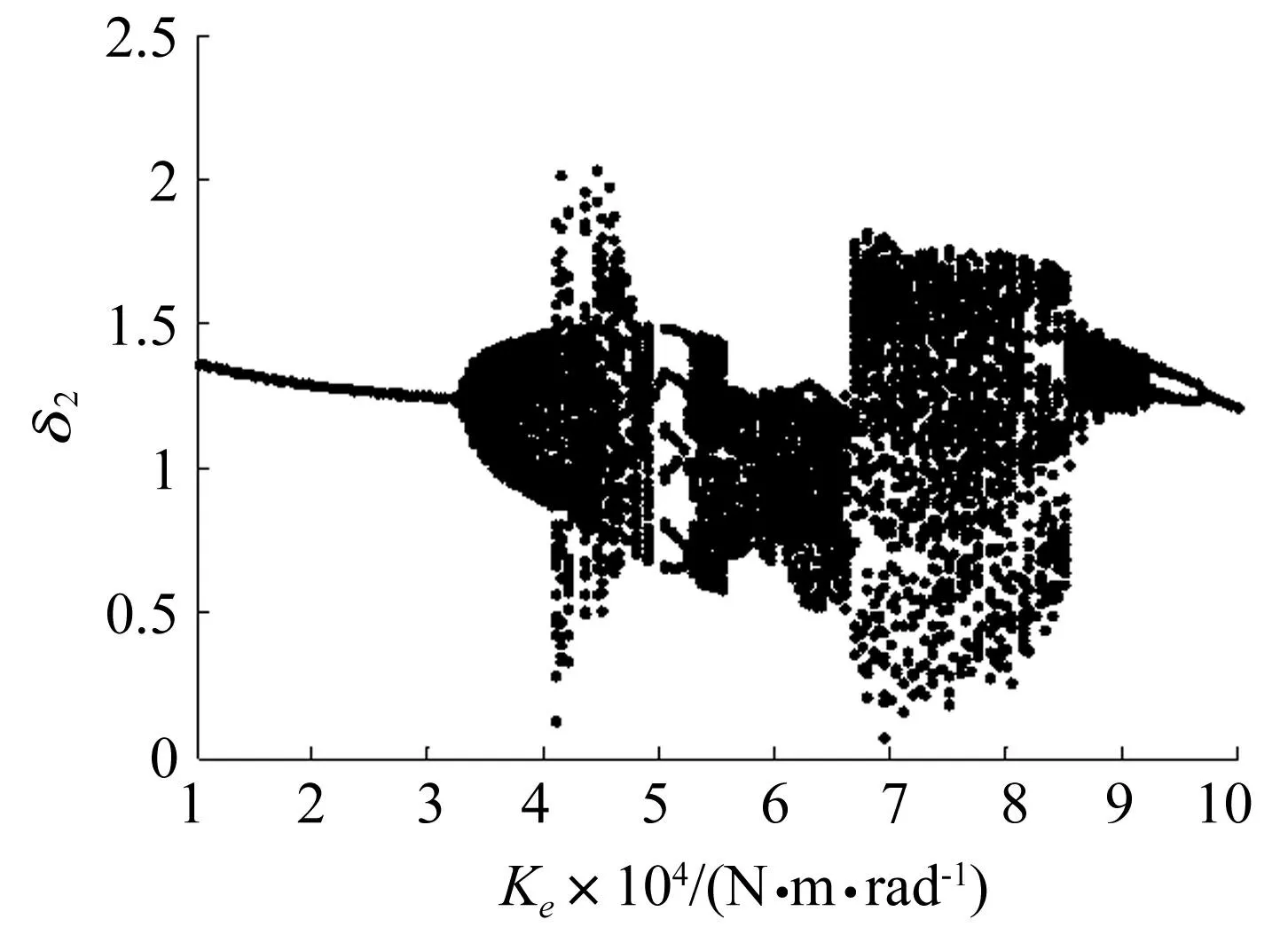
图10　转速2 500 r/min随扭簧刚度变化的分岔曲线 Fig.10 The bifurcation diagram depend on torsional stiffness of spring at 2 500 r/min

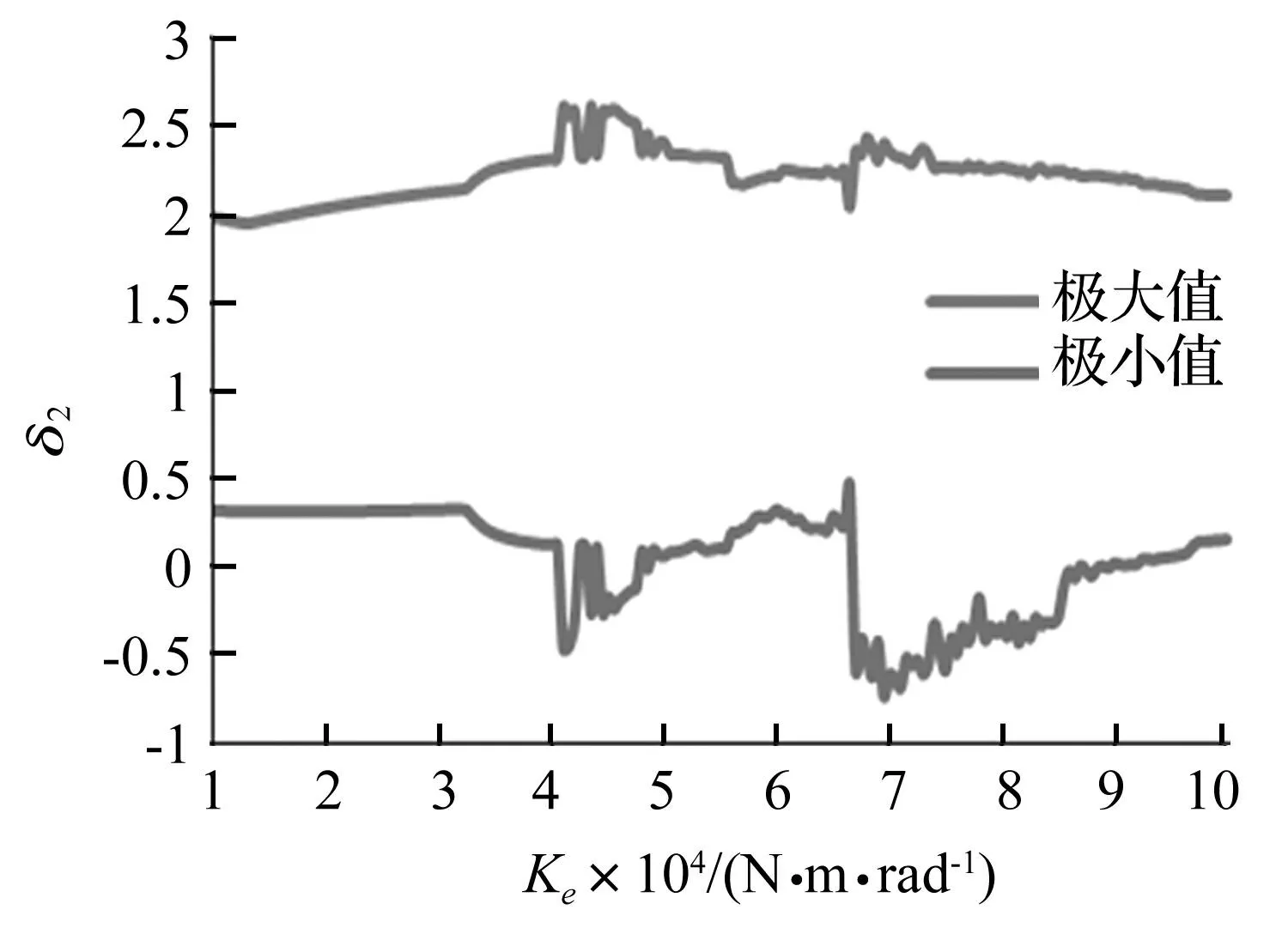
图11　转速2 500 r/min动态响应与扭簧刚度的关系 Fig.11 Relation between responses δ 2and torsional stiffness of spring at 2500r/min

结合图8～图11可知，扭簧刚度是影响系统非线性运动状态的重要因素，随扭簧刚度的变化，系统呈现出了丰富的非线性动力学特征，且不同转速下，系统动力学行为的变化规律不同；扭簧刚度对冲击现象的影响较小，扭簧刚度增大到一定值后反而会使冲击幅度增大，所以较小的扭簧刚度有利于消除冲击现象，但是扭簧刚度也不能过小，否则预变形量过大、超过屈服极限，将导致扭簧发生塑性变形。

4.3扭簧预紧力矩的影响

齿侧间隙为20 μm、扭簧刚度为5×104N·m·rad-1、转速分别为2 500 r/min、3 000 r/min时传动机构沿啮合线方向的无量纲相对位移δ1、δ2与加载扭簧预紧力矩的关系如图12所示。图12表明预紧力矩对固定齿轮和浮动齿轮的啮合状态均有重要影响，对浮动齿轮啮合状态的影响更加显著；预紧力矩较小时，浮动齿轮处于完全脱齿状态，此时只有固定齿轮与主动齿轮啮合，剪式齿轮成为普通齿轮；转速为3 000 r/min时，随预紧力矩的增加，冲击幅度逐渐减小，最终脱齿现象消失，进入正常啮合状态；转速为2 500 r/min时，随预紧力矩的增加沿啮合线方向的相对位移幅值增加，但系统始终处于正常啮合与瞬时脱齿之间，冲击现象一直存在。由此可知，加载扭簧的预紧力矩是影响剪式齿轮传动机构啮合状态的关键因素，合适的预紧力矩可以缓解或消除冲击现象的产生，但也不宜盲目加大预紧力矩，否则不但不能消除冲击现象，还会导致轮齿变形增大、齿间啮合力增加、齿面磨损加剧等。

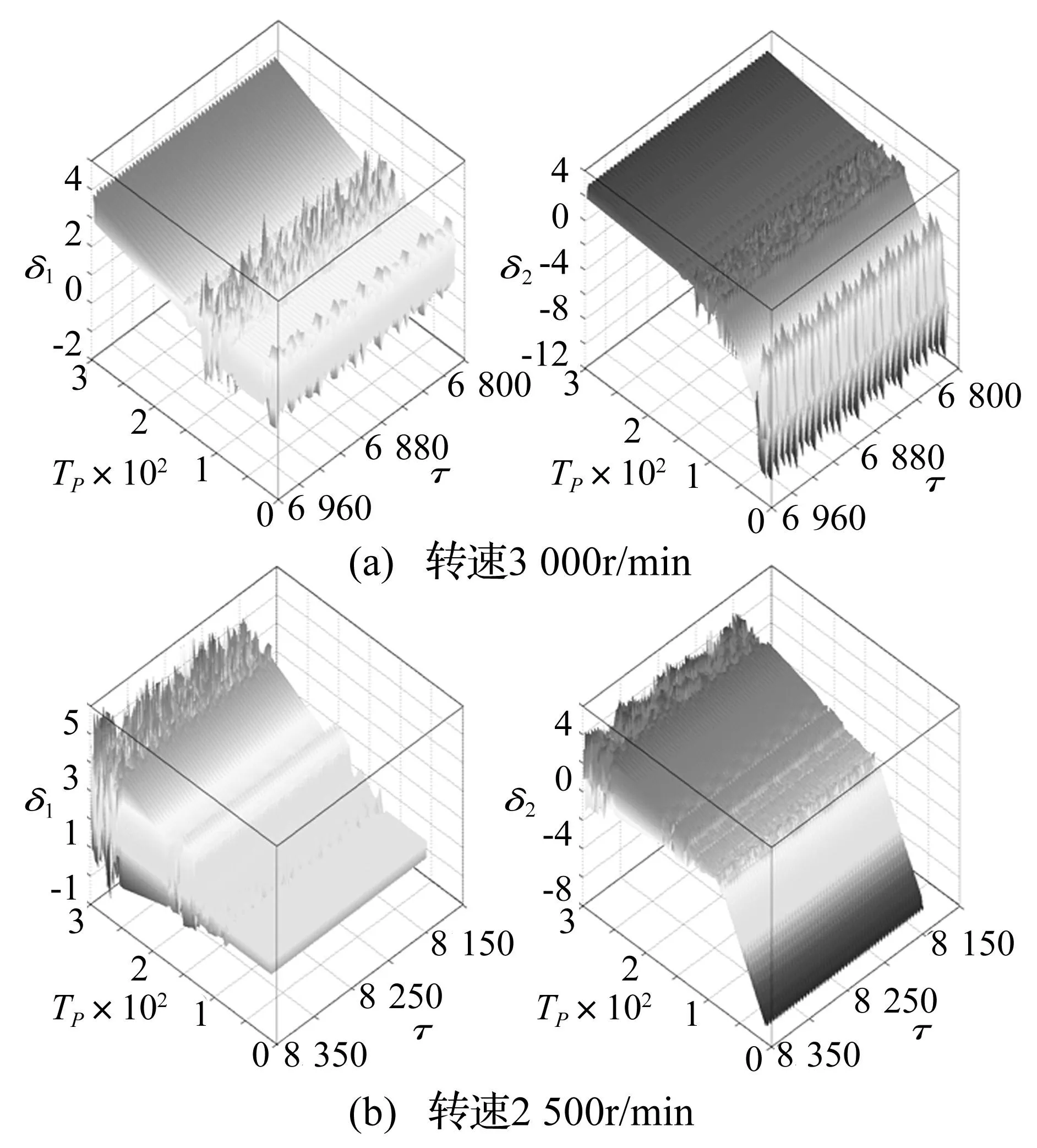
图12　动态响应与预紧力矩的关系 Fig.12 Relation between responses and preload of torsional spring

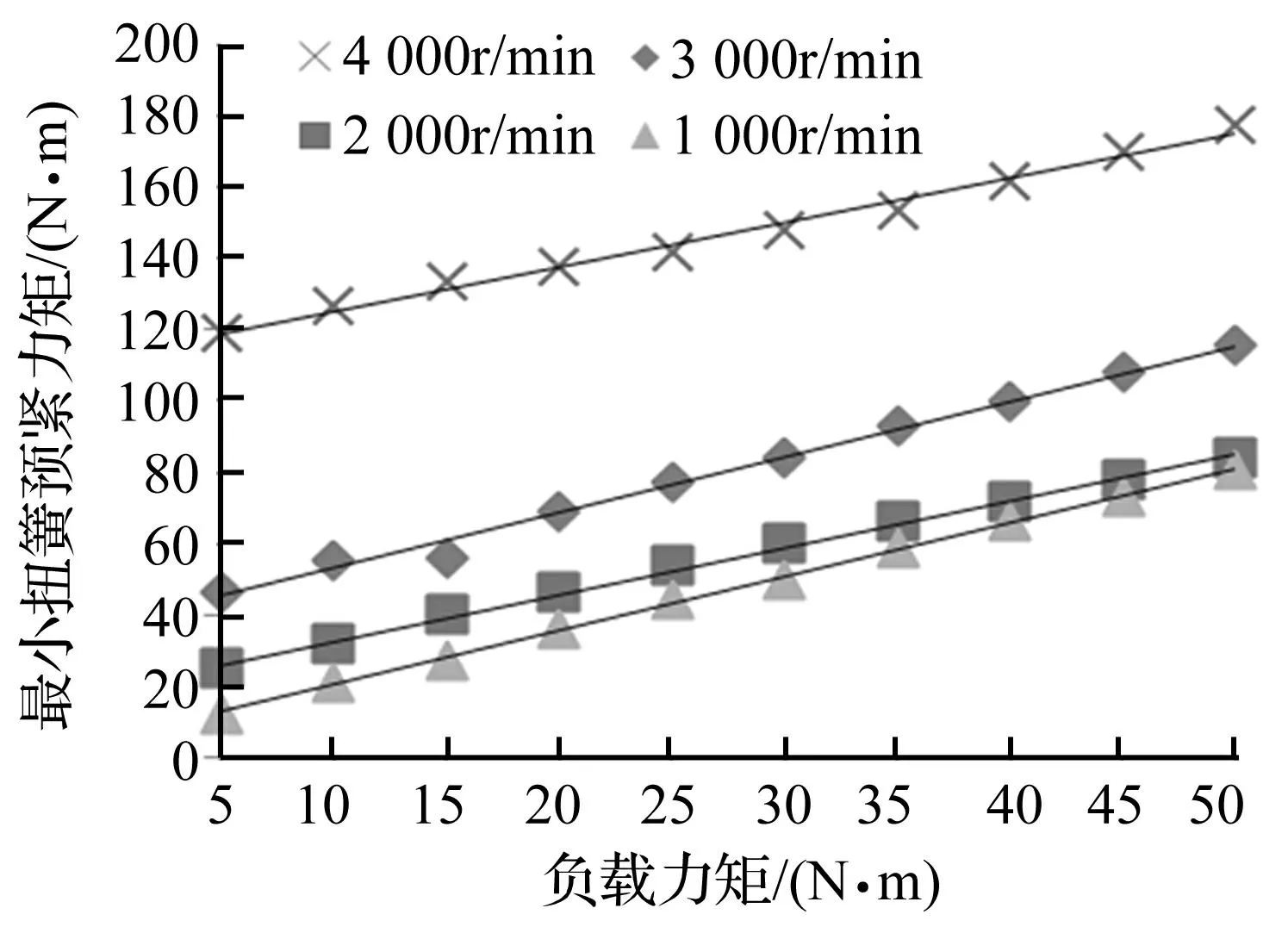
图13　不同转速时最小扭簧预紧力矩与负载的关系 Fig.13 Relation between minimum preload of torsional spring and drive torque at different speed

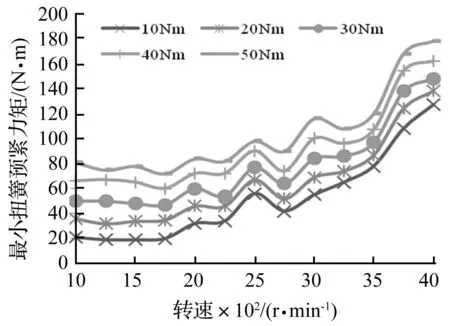
图14　不同负载时最小扭簧预紧力矩与转速的关系 Fig.14 Relation between minimum preload of torsional spring and speed at different drive torque

扭簧刚度取1.0×104N·m·rad-1、齿隙取20 μm，对基于啮合冲击[13]的最小扭簧预紧力矩Min_Tp的变化规律进行分析。图13给出了转速一定时Min_Tp与负载的关系，可以看出，Min_Tp随着负载的增加而近似线性增加，不同转速Min_Tp对负载变化的灵敏度略有不同。图14给出了负载一定时Min_Tp与转速的关系，可以看出，小于2 250 r/min的转速区间随转速升高Min_Tp变化较为平缓，Min_Tp约等于2倍负载力矩；在高转速区域转速对Min_Tp的影响显著，随转速的升高Min_Tp明显增加，Min_Tp等于(2～5)倍负载力矩。

5结论

(1)转速的变化对剪式齿轮传动系统混沌的产生有很大影响，随着转速的升高系统逐渐进入混沌状态；中等转速区间系统的非线性动力学行为对转速的变化更为敏感。

(2)齿隙间隙影响剪式齿轮传动系统动力学行为的复杂程度，随着齿侧间隙的增大，混沌区间增大，混沌特性加强。

(3)扭簧刚度是影响剪式齿轮传动系统非线性运动状态的重要因素，但对冲击现象的影响较小，较小的扭簧刚度更有利于消除冲击现象。

(4)加载扭簧的预紧力矩是影响剪式齿轮传动系统啮合状态的关键因素，合适的预紧力矩可以缓解或消除冲击现象的产生。最小预紧力矩的大小受负载力矩的影响且近似呈正比例关系。

参考文献

[1]高卫.弹簧消隙小模数齿轮传动链回差计算分析及工程应用[J].火控雷达技术,1999,28(4):31-34.

GAO Wei. Analysis of backlash in spring anti-backlash small modulus gear drive train and its engineering application [J]. Fire Control Radar Technology, 1999, 28(4): 31-34.

[2]石辉,杨锡和.双片齿轮用弹簧的弹性力计算[J].雷达与对抗, 2000(3):45-50.

SHI Hui, YANG Xi-he. Spring’s elastic force computation for double gear [J]. Radar & Ecm., 2000(3):45-50.

[3]董懿琼,杨雪春.无间隙齿轮在汽车发动机降噪中的应用尝试[J].南昌大学学报·工科版,2006,28(3):250-255.

DONG Yi-qiong, YANG Xue-chun. Experimental application of gapless gear pairs to noise reduction ofautomobile engine [J]. Journal of Nanchang University:Engineering & Technology, 2006, 28(3): 250-255.

[4]李国民.双片齿轮固有频率计算分析[J].电子机械工程, 2001(3): 11-12.

LI Guo-ming. Calculation and analysis of double gear’s inherentfrequency [J]. Electro-Mechanical Engineering, 2001(3): 11-12.

[5]Kwon Y S, Hwang H Y, Lee H R, et al. Rate loop control based on torque compensation in anti-backlash geared servo system [C]. American Control Conference, June 30-July 2,2004, Boston, MA, United Stated: Institute of Electrical and Electronics Engineers Inc, 2004: 3327-3332.

[6]Allan P M, Levy N M. The determination of minimum pre-load torque for anti-backlash gears in a positional servomechanism [J]. IEEE Transactions on Industrial Electronics and Control Instrumentation, 1980, 27: 1232-1239.

[7]杨政,尚建忠,罗自荣,等.扭簧加载双片齿轮消隙机构综合啮合刚度[J].机械工程学报,2013,49(1):23-30.

YANG Zheng, SHANG Jian-zhong, LUO Zi-rong, et al. Research on synthesis meshing stiffness of torsional spring-loaded double-gear anti-backlash mechanism [J]. Journal of Mechanical Engineering, 2013, 49(1): 23-30.

[8]Yang Zheng, Shang Jian-zhong, Luo Zi-rong. Effect analysis of friction and damping on anti-backlash gear based on dynamics model with time-varying mesh stiffness [J]. J. Cent. South Univ., 2013(20):3461-3470.

[9]日本机械学会.齿轮强度设计资料[M].李茹贞,赵清慧,译.北京:机械工业出版社, 1984:30-32.

[10]Benedict G H, Kelley B W. Instantaneous coefficients of gear tooth friction [J]. Transactions of the American Society of Lubrication Engineers, 1961, 4:59-70.

[11]李润方,王建军.齿轮系统动力学-振动、冲击、噪声[M].北京:科学出版社,1997.

[12]Wolf A, Swift J B, Swinney H L. Determining lyapunov exponents from a time series [J]. Physica D, 1985, 16:285-317.

[13]王峰，方宗德，李声晋.重合度对人字齿轮非线性系统振动特性的影响分析[J].振动与冲击,2014,33(3):18-22.

WANG Feng,FANG Zong-de,LI Sheng-jin.Effect of contact ratio on dynamic behavior of a double-helical gear nonlinear system[J].Journal of Vibration and Shock,2014,33(3):18-22.

第一作者段绵俊男，博士生，1982年生

第一作者唐晓慧男，硕士，1986年6月生

通信作者钱林方男，教授，博士生导师，1961年12月生