测控雷达布站与雷达精度试验航路设计研究∗

(中国人民解放军92941部队,辽宁葫芦岛125001)

0 引言

雷达精度试验是鉴定雷达性能指标的重要试验内容。雷达精度试验方法[1]主要依据雷达的精度指标、雷达测量数据特征及靶场具备的基本条件等,即根据靶场的场地、设备及试验技术条件,制定在接近实战条件下的外场试验方法。

精度试验一般采用比较法进行试验[2]。用选定的目标,按事先设计好的航路,作等速、水平、直线飞行。被鉴定雷达与靶场的测控设备按事先布局的位置进行布站,并在各自的引导设备引导下捕捉和跟踪目标,在同步信号的控制下,按设计好的录取间隔时间和数据总量,同步和连续地对目标进行测量和数据录取,并将各自测得的目标瞬时数据,按制定好的数据处理方案进行数据处理。

靶场的测控设备作为真值数据,对其精度的最低要求是:全航路的测量精度必须高于被鉴定雷达精度的3倍以上。对于雷达精度试验而言,目前靶场的测量设备有GPS相位差分、光测、雷测几种类型。光测设备受气象影响大,视场窄,捕捉目标困难,测量成功率低,作用范围小,而且随着距离的增加,位置精度下降,一般雷达精度试验不用。GPS载波相位差分定位技术的测量精度可达厘米级,为全天候测量技术,是雷达精度试验真值测量系统的首选,但是在某些试验中,加装GPS要对试验用飞行目标进行改装,困难很大,这时靶场一般采用测控雷达作为真值测量系统。但经过多次的实践发现,由于测控设备布站位置一般与所需鉴定雷达不同,数据经坐标转换后误差会放大,将其作为真值对被鉴定雷达精度会产生影响,不能盲目采用。本文主要探讨目标位置、靶场测控雷达和被鉴定雷达位置分布对测量精度误差的影响。

1 误差模型建立

雷达精度试验主要检测雷达距离精度、方位角精度和俯仰角精度是否满足指标要求[3]。一般雷达精度指标根据雷达体制和用途也略有差别,主要有系统误差μC、随机误差σC和最大误差(μC+3σC)[4]等。被鉴定雷达与测控雷达的坐标系一般均为北天东坐标系。处理精度时,需要把测控雷达测量参数(R,A,E)转换到以被鉴定雷达为坐标原点的坐标系中。

设测控雷达坐标系中的原点在以被鉴定雷达为坐标原点的北天东坐标系中的坐标为(a,b,c)。设任一点在测控雷达中坐标为(x,y,z),转到被鉴定雷达中为(x C,y C,z C)。

任一点用测控雷达(R,A,E)三参数表示为

转到被鉴定雷达中为

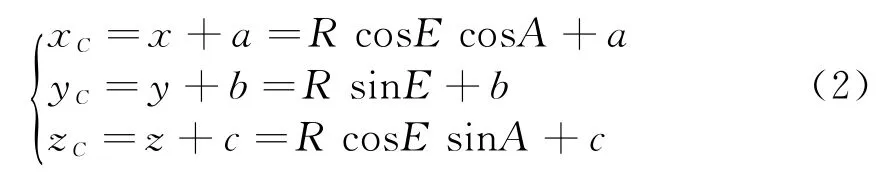
把测控雷达测量参数(R,A,E)转换到以被鉴定雷达为坐标原点的北天东坐标系中(R C,A C,E C),得到被鉴定雷达坐标中的参数(R C,A C,E C):

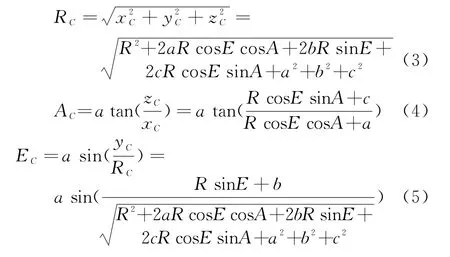
误差传递法[5]为:设函数y=f(x1,x2,…,x n),其中x1,x2,…,x n为具有均方根误差σx1,σx2,…,σxn、均值μx1,μx2,…,μxn的独立变量,函数y=f(x1,x2,…,x n)具有对每一个变量的连续偏导数。

则随机误差的精度分析模型为

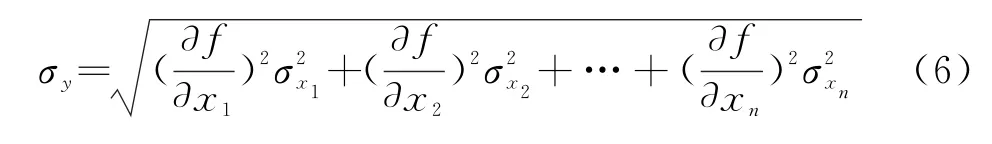
系统误差的精度分析模型为

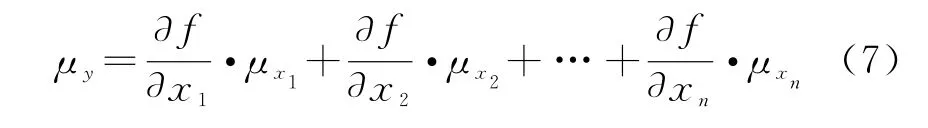
设μR,μA,μE为靶场测控雷达的距离系统误差、方位系统误差和俯仰系统误差;σR,σA,σE为靶场测控雷达的距离随机误差、方位随机误差和俯仰随机误差。

坐标转换后R C的系统误差(μRC)和随机误差(σRC)分别为

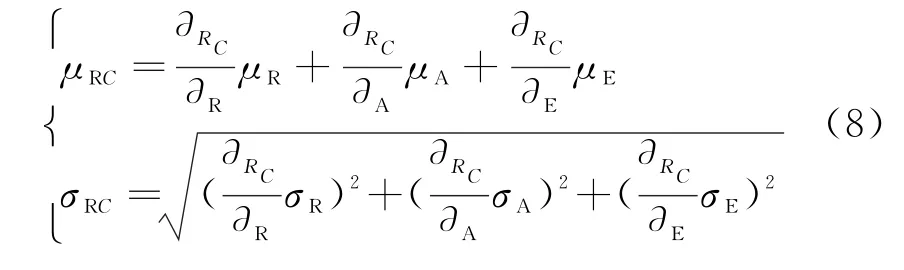
坐标转换后A C的系统误差(μAC)和随机误差(σAC)分别为

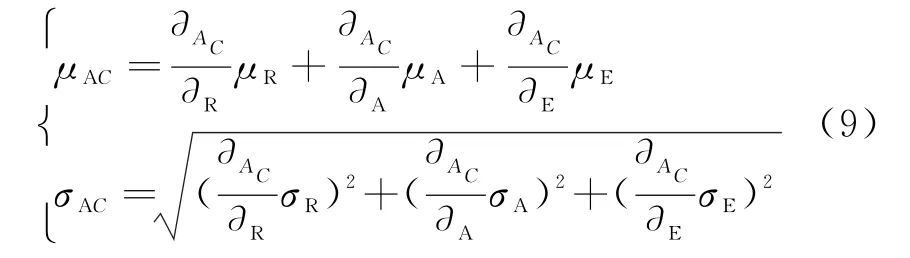
坐标转换后E C的系统误差(μEC)和随机误差(σEC)分别为

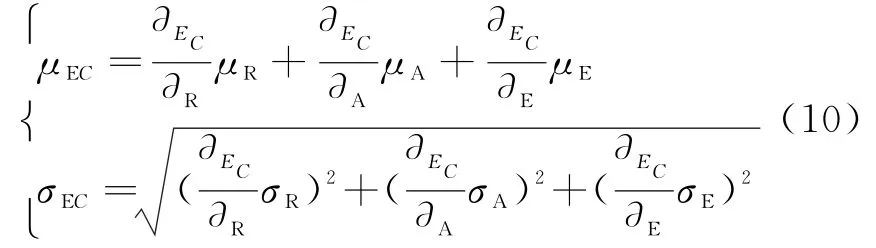
式(3)～(5)分别对(R,A,E)求偏导并代入式(8)～(10)即可求解R C,A C,E C的系统误差和随机误差。

2 仿真分析

在雷达精度试验方案设计时要考虑测控雷达、被鉴定雷达的位置,要设计目标的飞行航路。这3个因素的相对变化会带来测控雷达距离、方位角、俯仰角随机误差和系统误差变化。本文根据靶场试验的实际情况对测控雷达的精度误差与目标航路、靶场测控雷达、被鉴定雷达位置分布的影响分别进行分析。

设测控雷达与被鉴定雷达相距R C1、方位角A C1、俯仰角E C1。则在北天东坐标系中(a,b,c)分

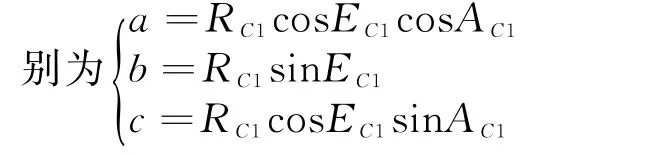
雷达精度试验时,目标沿规定航路由远及近飞入,测控雷达、被鉴定雷达和目标位置的关系如图1所示。

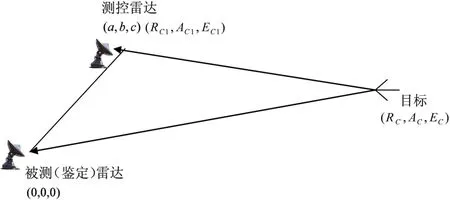
图1 雷达精度试验航路示意图

2.1 测控雷达精度分析

当被鉴定雷达、测控雷达、目标航路由于靶场地势的局限性均固定时(即a,b,c,A C均为定值),可根据函数测量误差理论,计算测控雷达的距离、方位角、俯仰角随机误差和系统误差经坐标转换后是否满足被鉴定雷达对真值精度的要求。如图1所示,设测控雷达距被鉴定雷达距离50 km,偏离被鉴定雷达方位50°,高度200 m,即a=38 302,b=32 139,c=200;目标航路为进入距离200 km (距被鉴定雷达),进入航向为250°,退出距离为4 km;设测控雷达距离、方位角和俯仰角精度随机误差分别为3 m,0.01°,0.01°,系统误差分别为5 m,0.02°,0.03°,可以看到测控雷达的距离、方位角、俯仰角精度误差在目标全航路的变化情况(其中总误差为系统误差与3倍的随机误差之和)。

以目标距被鉴定雷达距离为横坐标,从图2的仿真曲线上可看到在全航路上测控雷达的方位角、俯仰角、距离的系统误差精度与随机误差的变化。设被鉴定雷达的距离、方位角、俯仰角的精度指标:系统误差为50 m,0.3°,0.3°;随机误差为15 m,0.1°,0.1°。根据雷达精度试验数据处理原则,即真值精度必须大于被鉴定雷达精度3倍以上,则测控雷达测量目标数据可作为真值的可用区间段为:距离数据可用段16～113 km,方位角数据可用段11～200 km,俯仰角数据可用段12～200 km。因此在雷达精度试验的准备阶段,需要根据被鉴定雷达和测控雷达的相对位置和既定的目标航路,利用误差传递模型推算测控雷达测量的目标数据可作为真值使用的区间段,以此指导试验的开展。

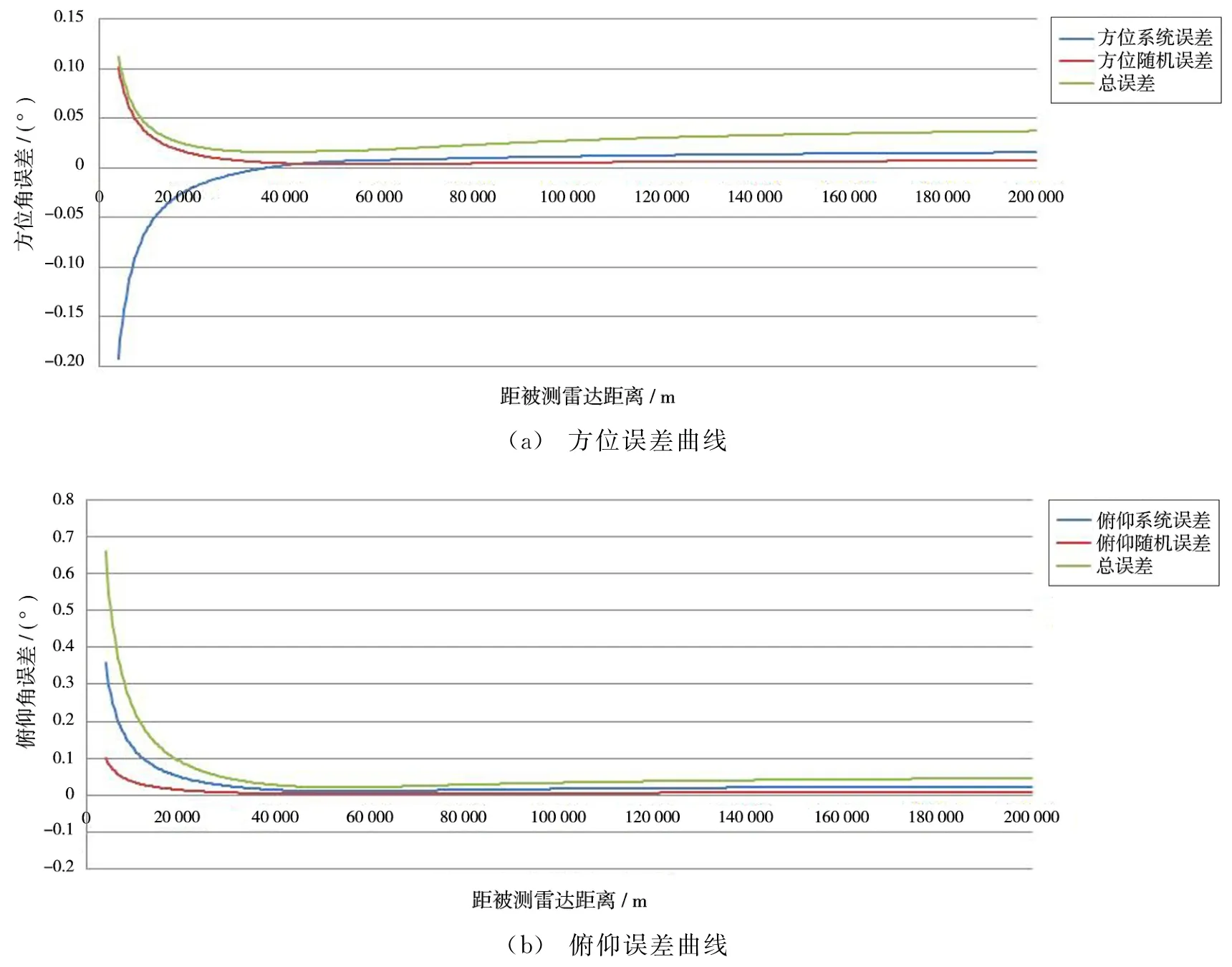
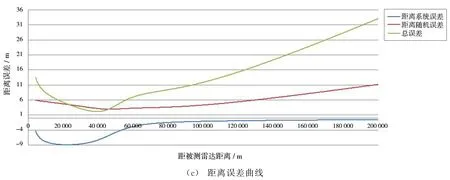
图2 全航路误差曲线图

仿真分析可以看到,当被鉴定雷达与测控雷达位置不一致时,测控雷达的方位角、俯仰角、距离精度均有传递误差,且随着目标与被鉴定雷达和测控雷达的相对位置变化而变化。对方位角、俯仰角精度来说,目标离被鉴定雷达与测控雷达距离越远,方位角和俯仰角真值精度误差越小,并趋于测控雷达本身的精度水平;随着目标距离越近,误差逐渐增大,但变化不明显。在目标相对测控雷达过航,即目标航向、目标与测控雷达的连线夹角约90°(在图2中约50 km处)时方位角和俯仰角误差迅速增大。通过原因分析,在目标相对测控雷达过航时,导致方位角和俯仰角系统误差形成的偏导数计算结果迅速变大,因此方位角和俯仰角误差迅速变大。

对距离精度来说,目标距被鉴定雷达越远,距离误差越大,随着目标的进入,距离精度逐渐减小,当目标相对测控雷达过航时,距离误差达到最小,随着目标距离的进入,误差逐渐增大。而在过航时,由于距离误差偏导数计算结果为最小值,因此距离误差此时最小。

因此在雷达精度试验时,若被鉴定雷达的方位角和俯仰角指标较高,则相应地对测控雷达精度的要求也非常高,当测控雷达精度达不到全航路使用要求时,可通过减小目标相对测控雷达过航距离达到延长测控雷达对目标的俯仰角和方位角测量数据可用的区间长度,主要措施是在航路规划过程中,合理规划目标飞行路线,尽量径向于测控雷达飞行,如可以沿固定径向航线往复飞行,减少转弯半径或在转弯过程中的试验数据不作为评定依据。

2.2 目标航路选择

当靶场测控雷达位置和被鉴定雷达位置均固定不变,但目标航路可调整(即R为定值,A C可变化)时,目标航路的调整对测控雷达传递误差的影响如图3所示。取A C分别为15°,20°,25°,其余参数不变。

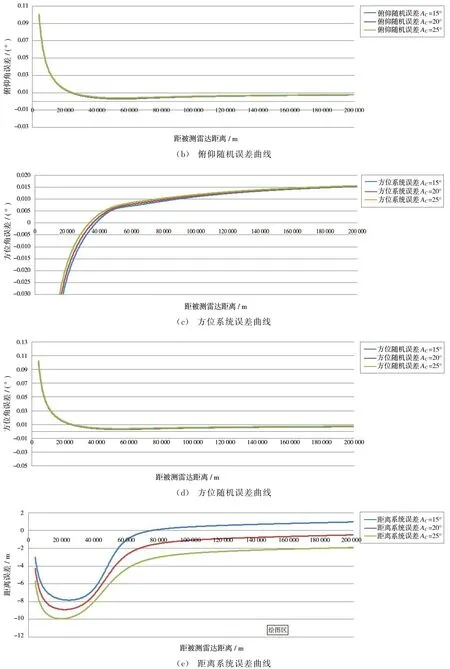
由图3可见,A C(目标航路)的变化对方位角和俯仰角误差精度影响不明显,对距离误差精度影响明显。仿真分析可见,随着A C的增大或减小,距离误差也随之增大或减小。通过计算分析,在A C值较小时,由式(8)可得,此时形成距离误差的各因子偏微分求导加权后值最小。

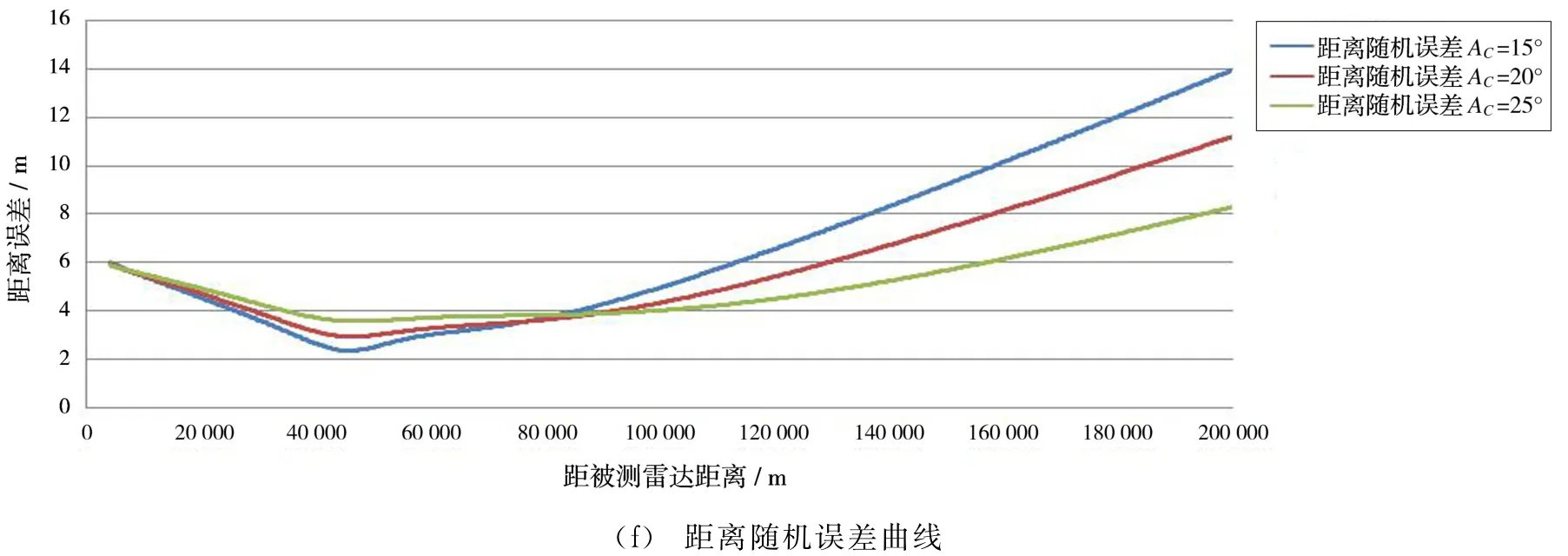
图3 俯仰角、方位角和距离误差曲线

因此,在对雷达距离精度要求较高试验方案设计时,若目标航路可调整,则尽量选用较小的A C值,以减少测控雷达距离精度误差。

3 结束语

本文对测控雷达布站位置引起的真值精度误差进行了分析与建模,并对测控雷达、被鉴定雷达和目标航路三个位置相对变化引起的测控雷达的距离、方位角、俯仰角随机误差精度和系统误差精度进行了仿真分析。结果表明,在雷达精度试验方案设计时,首先需要根据被鉴定雷达和测控雷达的相对位置和既定的目标航路,利用误差传递模型推算测控雷达测量的目标数据可作为真值使用的区间段。当测控雷达精度达不到全航路使用要求时,可通过减小目标相对测控雷达过航距离达到延长测控雷达对目标的俯仰角和方位角测量数据可用的区间长度。若目标航路可调整,则尽量选用较小的A C值,以减小测控雷达距离精度误差。得出的结论对今后雷达精度试验方案设计和结果评估工作有重要的实际意义。

[1]中国人民解放军总装备部军事训练教材编辑工作委员会.雷达试验[M].北京:国防工业出版社,2004: 147-148.

[2]姜来春.高精度测量雷达动态精度分析方法研究[J].电子科技,2014,27(7):51-53.

[3]杨琳,朱元昌,邸彦强,等.雷达动态精度试验误差统计分析方法改进[J].测控技术,2014,33(9):48-51, 55.

[4]张海成,杨江平,王晗中.大型跟踪测量雷达的卫星标定方法研究[J].雷达科学与技术,2014,12(5):470-472,481. ZHANG Haicheng,YANG Jiangping,WANG Hanzhong.Study on Satellite Calibration Method for Tracking and Instrumentation Radar[J].Radar Science and Technology,2014,12(5):470-472,481.(in Chinese)

[5]王春明.坐标转换误差传递模型的建立及靶场试验应用研究[J].信息技术与信息化,2013(6):109-112.