电磁盲区随波导内雷达发射角的变化特性∗

张 瑜,赵春丽

(1.河南师范大学电子与电气工程学院,河南新乡453007;

2.河南省高等学校电磁波特征信息探测重点学科开放实验室,河南新乡453007)

0 引言

蒸发波导是海洋大气环境中经常出现的一种特殊的表面波导,一般发生在海洋大气环境40 m高度以下的近海面低层大气中,能使雷达电磁波产生异常现象[1]。一方面可以使得电磁波实现超视距传播,扩大雷达的探测范围,另一方面也会形成新的雷达电磁盲区[2-3]。电磁波在蒸发波导传播需要满足一定的条件,它不仅与雷达发射源位置、雷达电磁波波长、蒸发波导的特征参数等有关,还与雷达发射角有关[4]。只有当发射角小于临界角时,雷达电磁波才能在蒸发波导中形成波导传播,从而实现视距探测。

目前,国外在大气波导传播方面的研究仍处于领先地位,如美国、俄罗斯、澳大利亚等国都已经建立了反映大气波导传播效应的预报系统[5]。国内对大气波导的研究主要集中在蒸发波导以及对雷达性能的影响等方面。要想真正利用蒸发波导环境实现雷达超视距探测,就必须首先搞清楚电磁波在该环境下的传播特征。我国虽然在这方面已经取得了一定的研究成果,但是关于电磁盲区随雷达发射角的变化情况还没有得到深入的研究。另外,在有蒸发波导情况下,当雷达发射角被限制在临界角范围内时,雷达电磁波会产生超视距传播现象,但不同的发射角产生的雷达盲区不同,从而在不同程度上影响雷达的探测性能。本文主要研究在临界角范围内,电磁盲区随雷达发射角的变化规律,为实际应用蒸发波导实现雷达超视距探测奠定基础。

1 雷达电磁盲区计算方法

目前,描述大气波导内的电磁波传播问题主要有两种方法。一种是抛物方程法,它是对电磁波波动方程,即亥姆霍兹方程的一种近似,可对沿近轴传播方向锥形区域内的电磁能量传播进行有效的模拟。目前抛物方程结合其他有效的数值算法可对远距离电磁波传播问题提供快速数值解[6]。另一种是射线描迹法,在频率很高情况下,电磁波传播可以用几何光学理论进行近似。射线描迹法是几何光学理论在对流层电波传播问题中的一种演化,跟踪这些射线路径不仅可以清晰地描绘出比较清晰的物理图像,而且可以对大气波导传播这种特有的现象进行形象的描述[7]。尽管这两种方法的机制不同,但是在描述大气波导内的电磁波传播都有较好的特点。

1.1 抛物方程法

由Maxwell方程可知,雷达电磁波的电场分量和磁场分量具有一定的对称性,即

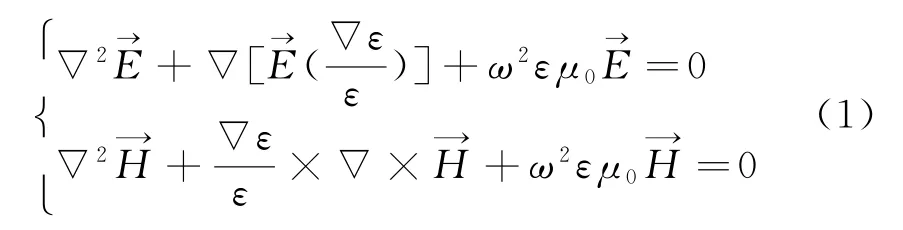
若只考虑地球表面水平极化的电偶极子辐射源情形,球坐标系下的非零场分量为H r,Hθ和Eϕ,则式(1)可化为标量形式:

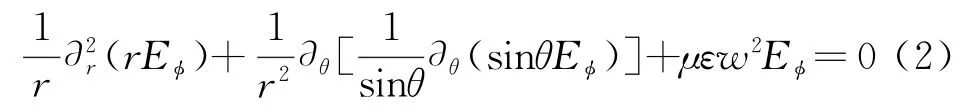
对式(2)进行推导,得到电磁波的抛物方程[8]为

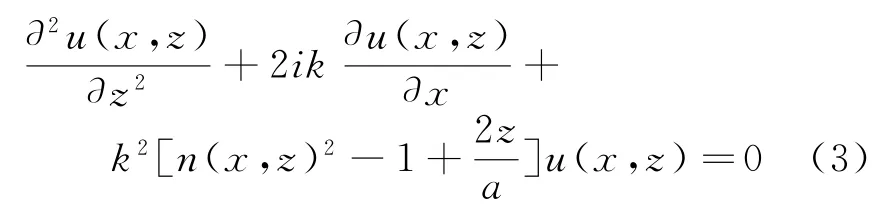
式中,u(x,z)为电场或磁场的强度,k为自由空间波数,a为地球平均半径,n(x,z)为高度z和距离x二维空间上的大气折射指数。

目前,步进傅里叶算法和有限差分法是求解抛物方程的两种常用数值解法。经比较发现,步进傅里叶算法具有较好的稳定性和有效性[6]。另外,结合初始场条件和边界条件可以很好地求解出蒸发波导中任意一点的电磁波场强值。

在式(3)中,若已知u(x0,z),则对其作傅里叶变换可得

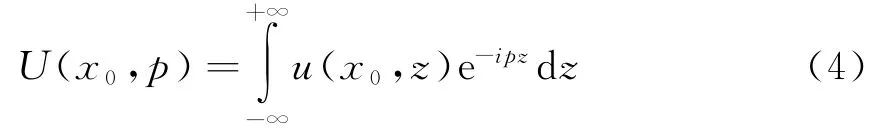
对于距离增加Δx的解为

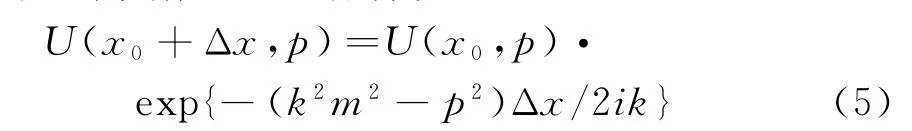
对式(5)进行傅里叶反变换可得

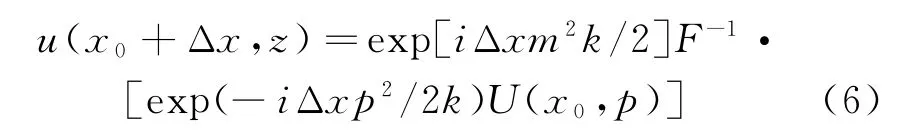
式中:Δx为水平方向距离间隔,即步长;p为变换中的变量,通常被称为垂直波数或空间频率。p= ksinθ,θ为雷达发射角,即雷达发射方向与水平面间的夹角,如图1所示。

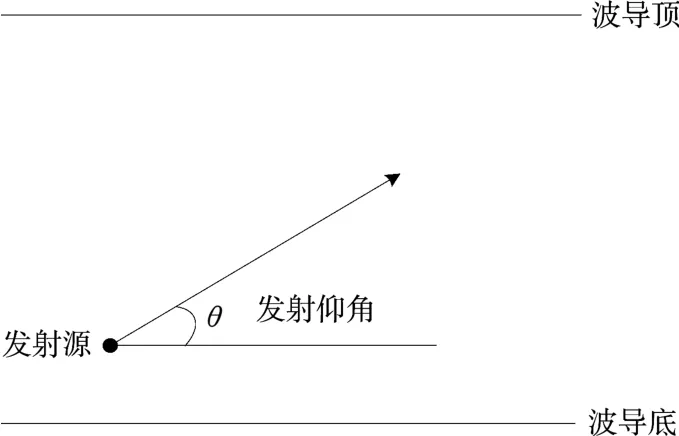
图1 雷达发射仰角示意图

使用步进傅里叶算法须从初始场开始计算,则须知道计算初始场的条件,如发射方式、远场方向图、天线高度。另外,在求解过程中还须对z空间进行截断[5]。

衰减损耗因子反映了大气折射、海平面反射和气体分子吸收等因素的影响,体现了实际环境导致的电波单程传播衰减程度,基于式(6)可得出电磁波在蒸发波导中的传播损耗为

在电磁盲区的计算中,首先在高度-距离二维空间上设定一定间隔的网格,利用式(7)计算出每一网格点上的电磁波传播损耗值后与限定的雷达接收门限值[6]进行比较,当某一网格点处电磁波传播损耗值小于雷达接收门限值时,选中该网格点。将全部网格逐一进行比较后,所有选中的网格点形成的区域则为雷达电磁波探测区域。相应地,所有未被选中的网格点所围成的区域则为无线电盲区。

1.2 射线描迹法

采用修正折射指数m=n(1+h/re),将球面等效成平地面,根据电磁波传播理论可知,大气高度h1和h2处对应的修正折射指数m1和m2与入射角θ1和θ2满足斯奈尔定律[5],即

在蒸发波导中,雷达的探测角度θ1,θ2都在零度附近,则可将式(8)进行泰勒二阶级数展开后变为

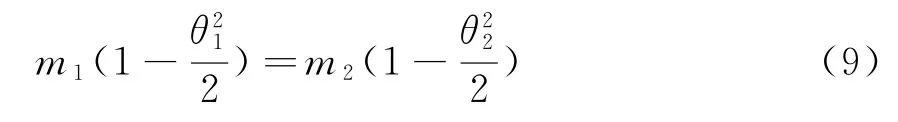
一般情况下,低层大气修正折射指数接近于1,则式(9)可简化为

若大气修正折射指数在h1和h2间随高度线性变化率为g,则结合式(10)可得

将式(11)写成微分形式为

另外,地面距离增量与高度步长的关系为

则结合式(12)与式(13)可得

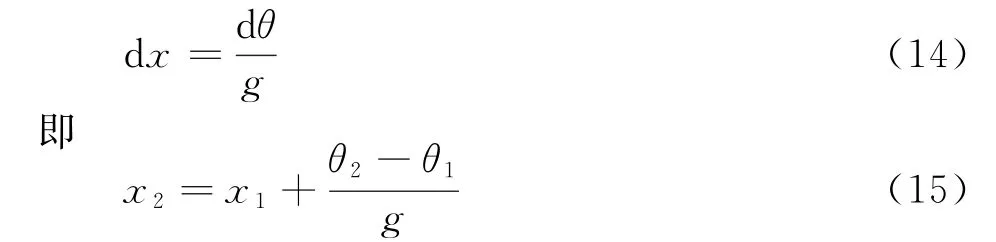
在已知大气修正折射率的垂直梯度值g、初始仰角θ1、初始高度h1和传播距离x2-x1的情况下,利用式(11)和式(15)就可以连续地确定电磁波射线的传播轨迹。

当发射仰角不同,电磁波单次跳跃的最大距离不同。每一种情况下,射线首次到达最高点处后会形成两个分支。一个分支凹向上传播,另一个分支凹向下在波导内以全跳方式绕地球连续传播。在射线到达的最高点以上及凹向上的分支以外形成一个完全没有射线可以到达的阴影区域,这个区域就是无线电盲区。

2 仿真分析

已知某型号雷达的频率为9 380 MHz,峰值功率为10 k W,脉冲宽度为0.3×10-6s,脉冲重复频率为600 Hz,天线增益为28 d B,系统损耗为3 d B,水平波束宽度为1.3°,天线转速为25 rad/min,噪声系数为14 d B,天线高度为25 m,波导内修正折射率梯度为-143 N/km,波导上方修正折射率梯度为117 N/km。

选择某海域蒸发波导实测参量的平均值,经计算雷达电磁波所对应的临界发射仰角为0.004 rad。利用抛物方程法得到的雷达电磁盲区分布图如图2所示。

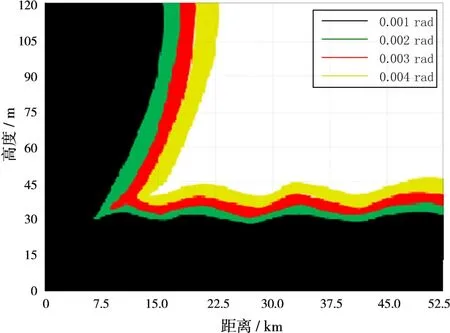
图2 基于抛物方程法得到的雷达电磁盲区分布图

由图2可知,在临界发射仰角内,随着雷达天线发射仰角的增大,通过抛物方程可知每一网格点上的电磁波传播损耗值相对变小。因雷达接收门限值是恒定不变的,则在电磁波传播损耗值小于雷达接收门限值这种情况下,所对应的网格点数增多,即雷达依一定探测概率和虚警概率可检测到更多的目标,也就是说雷达的可探测范围增大,因此所对应的电磁盲区范围变小。当发射仰角继续增大到临界角时,每一网格点上的电磁波传播损耗值相对更小,则对应的网格点数更多,因此在这种情况下,雷达探测范围将达到最大,此时所对应的雷达盲区范围将达到最小。

利用射线描迹法得到的雷达电磁盲区分布图如图3所示。

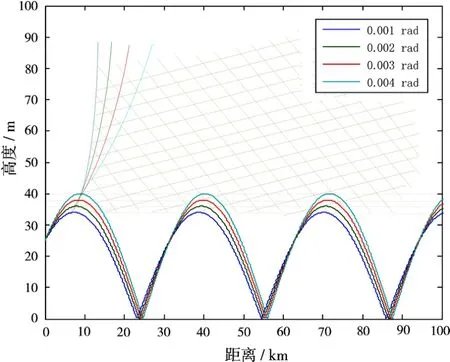
图3 基于射线描迹法得到的雷达电磁盲区分布图

由图3可知,在临界发射仰角内,随着雷达天线发射仰角的增大,使得雷达电磁波射线首次达到的峰值增大,且在峰值处产生的凹向上的这条分支逐渐向右平移,则在射线达到的峰值以上和凹向上的分支以外形成的阴影区域变小,即无线电盲区变小。当发射仰角逐渐增大到临界角时,峰值以上和凹向上的分支以外所形成的阴影区域达到最小,也就是说无线电盲区范围达到最小。

由图2和图3分析可知,抛物方程法和射线描迹法都能对电磁波传播轨迹进行预测,且能够准确给出电波覆盖区域、盲区范围。这两种方法得到的电磁盲区随雷达天线仰角的变化规律一致。

3 结束语

由本文可知,电磁波越接近临界角,盲区范围越小。另外,由于雷达天线发射仰角易于控制,因此在实际架设和使用雷达时,应尽可能保持雷达发射仰角接近临界仰角,从而增大探测范围,获取更多更可靠的目标信息。

电磁波在大气波导中传播不可避免地发生雷达盲区的现象,雷达盲区既是巡航导弹突防的最佳路径,又是防御的薄弱环节,最易遭敌飞机、导弹的突袭,因此如何充分地利用电磁盲区非常重要。这就需要我方一方面可以在战术上有效地利用攻击机或巡航导弹进行突防;另一方面也应采取适当的补救措施进行防御,比如可以用高空预警机进行补盲或者用多天线等技术。

[1]成印河,张玉生,赵振维,等.冬季南海北部近岸蒸发波导环境分析[J].电波科学学报,2013,28(4):697-703.

[2]董鹏曙,金加根,谢幼才,等.天线副瓣对雷达探测的影响研究[J].雷达科学与技术,2014,12(1):112-115. DONG Pengshu,JIN Jiagen,XIE Youcai,et al. Study on Influence of Antenna Sidelobes on Radar Detection[J].Radar Science and Technology,2014,12 (1):112-115.(in Chinese)

[3]康士峰,曹仲晴,王红光,等.基于目标函数的微波超视距雷达天线高度优化方法[J].电子与信息学报, 2014,36(7):1767-1770.

[4]胡荣旭,吴振森,张金鹏.中国近海蒸发波导反演中最佳雷达参数分析[J].电波科学学报,2015,30(4): 653-660.

[5]康士峰,张玉生,王红光.对流层大气波导[M].北京:科学出版社,2014.

[6]焦林,张永刚.大气波导条件下雷达电磁盲区的预报研究[J].西安电子科技大学学报,2007,34(6):989-994. JIAO Lin,ZHANG Yonggang.Prediction of the Electromagnetic Shadow Zone Under the Atmospheric Duct[J].Journal of Xidian University,2007,34(6): 989-994.(in Chinese)

[7]高超,周朋.基于射线追踪理论的超视距通信盲区分布研究[J].兵器装备工程学报,2016,37(1):132-135.

[8]KUTTLER J R,DOCKERY G D.Theoretical Description of Parabolic Approximation/Fourier Split-Step Method of Representing Electromagnetic Propagation in the Troposphere[J].Radio Science,1991, 26(2):381-393.

赵春丽女,1991年生,河南商丘人,河南师范大学电路与系统专业硕士研究生,主要从事大气波导探测与雷达超视距探测技术研究工作。