基于PRI变换的混叠LFM雷达信号分选∗

朱文贵1,刘 凯,韩嘉宾

(1.中国电子科技集团公司第五十一研究所,上海201802; 2.上海大学通信与信息工程学院,上海200072)

0 引言

现代战争是集海、陆、空、天、电子战为一体的多维的、非接触的、高科技的战阵。雷达与对抗作为现代战争的重要组成部分,必将随着电子技术的发展愈演愈烈[1]。由于现代电磁环境的复杂化,雷达脉冲信号在时域上的混叠越来越严重,如何从密集、混叠的雷达脉冲流中准确地分离出各部雷达脉冲序列是当前雷达信号分选的研究重点[2]。线性调频(Linear Frequency Modulation, LFM)作为最常见的脉冲压缩技术[2],其目的是解决雷达监测能力和距离分辨率之间的矛盾,被广泛应用在现代雷达技术中。因此,针对LFM雷达信号的分选也是当今雷达信号分选的热点。

在当前的雷达信号主分选方法中,利用到达时间(TOA)来估计脉冲重复间隔(PRI)是最常用的方法,现实工程应用中采用较多的方法有扩展关联法、累计差直方图(CDIF)法、序列差直方图(SDIF)法等。由于这些方法会带来二次以及高次谐波的问题,即在PRI整数倍的地方也会出现峰值,造成PRI检测不准确,因此PRI变化法以及众多改进的PRI变化[3]陆续被提出。当雷达脉冲混叠比较严重,致使脉冲信息丢失较多时,上述方法的分选效果会急剧下降,为了解决此问题,陈晓军等[4]提出盲源分离的方法,将目标源信号从混合信号中分离出来。童姗等[5]提出运用独立分量分析解决雷达信号分选中的未知混叠信号的问题,其根据输入源信号的统计特性,通过选择判据和优化算法将信号分解成若干个独立的源成分,完成混叠信号的分离。由于电磁环境的复杂化,基于脉间特征的雷达信号分选性能难以达到要求,因此有学者采用雷达信号的脉内特征[6]实现雷达分选,也取得了很大的突破。脉内特征相对于脉间特征,虽然具有普遍性、稳定性、唯一性和可测性等优势,但是针对绝大部分的脉内特征分选方法而言,其计算复杂度太大,造成不能实时地实现雷达信号的分选,故不能达到工程应用上的要求。

针对上述情况,本文提出了一种基于PRI变换的脉冲去混叠LFM雷达信号分选算法。通过对接收到的LFM雷达信号进行小波变换[7],估计脉冲信号的起始时刻和终止时刻,对混叠的脉冲信号而言,检测估计丢失脉冲的起始时刻和终止时刻,利用基于PRI变换法得到实现PRI的估计。

1 脉冲恢复

1.1 混叠信号模型

当两个脉冲交叠时,两个旧的脉冲合并成一个新的脉冲,其脉冲信息随着混叠而变化,致使原本的两个脉冲到达时刻演变成只有一个脉冲到达时刻,造成雷达脉冲的丢失,给雷达分选造成一定的困难。雷达混叠示意图如图1所示。

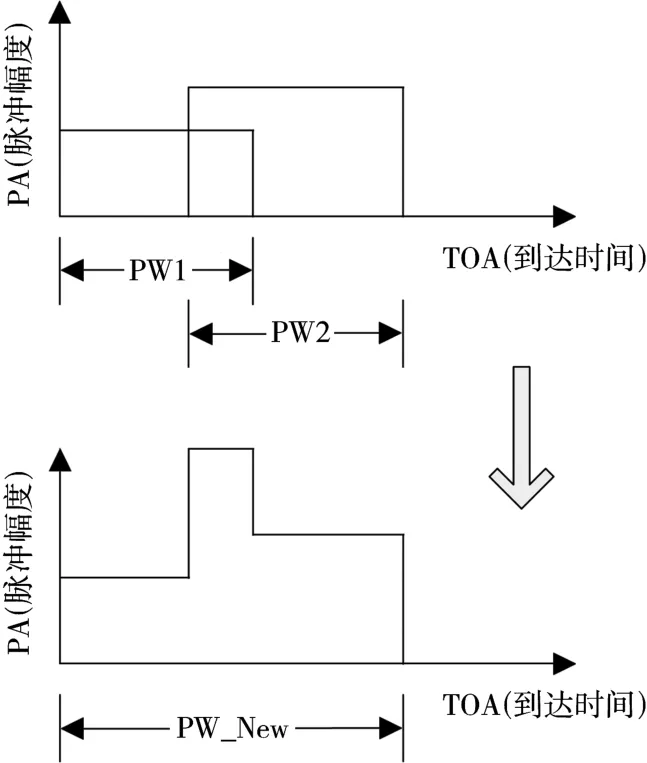
图1 脉冲混叠示意图

混叠LFM信号是由多个LFM信号叠加而成,其信号模型可以表示为

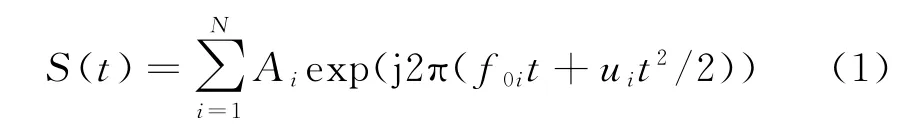
式中,A i为信号幅度,f0i为信号载频,u i为信号调制指数。由于混叠的原因,输出信号为一混合信号,其参数为混合后的参数,而非几个独立的LFM信号参数。

所提出算法解决的问题是如何通过混叠的脉冲信息还原出原始混叠LFM雷达的脉冲信息,实现还原丢失脉冲信息的LFM雷达信号分选。

1.2 信号小波时频分析

小波基的选取关系着信号时频特性的好坏,所以应选取时频域特性都比较好的小波函数, Morlet小波基具有较好的时频聚集性,且为渐近性信号。Morlet小波函数表达式为

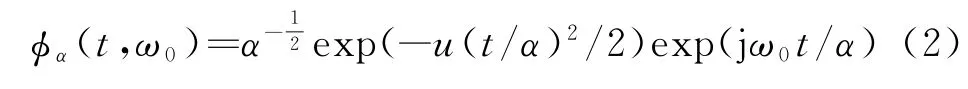
其傅里叶变换为

若信号的采样频率和小波的采样频率相同的话,小波尺度与频率之间的关系是α=f0/f x(α为伸缩尺度,f0为采样频率)。式(2)中,u为尺度加权因子,它决定了Morlet小波的窗口大小;ω0为小波变换的基频;α对应频率为ω0/α。由式(3)可得Morlet小波的中心频率在ω=ω0/α处。

对于任意采样信号s(n Ts)=Aexp(-jω1n T),则信号的Morlet小波变换定义为ω(α,n Ts),Ts为采样周期。

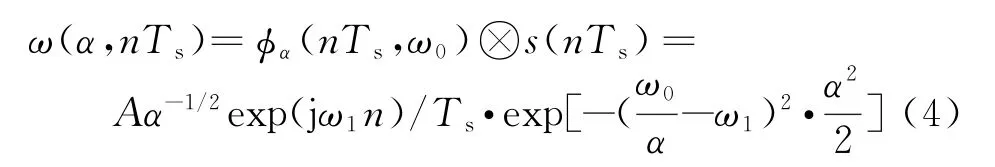
式中,⊗表示卷积。

由式(4)可得信号经小波变换后幅值的模为

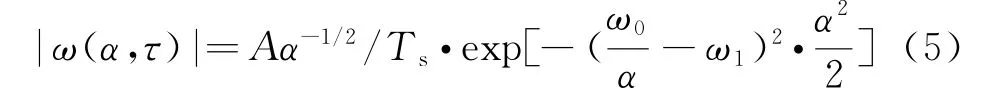
由式(5)可知,当ω0/α=ω1时,|ω(α,τ)|取得最大值。即函数|ω(α,τ)|在ω0/α=ω1处取得最大值,这表明信号在频率ω1上能量最集中。

1.3 混叠脉冲到达时间(TOA)估计

1.3.1 时频数据二值化

对LFM信号进行时频变换后,运用本文提出的算法就可以实现对丢失脉冲实现还原,还原丢失的信号信息。

对接收信号进行小波时频变换得到信号是信号的时频变换结果WT(α,n),同时采用等高线截取法对小波变换的数据进行截取,为了能够较好地反映信号的时频特性且受噪声影响程度较小,等高线阈值的选取影响着参数估计的好坏,本文选取等高线门限为

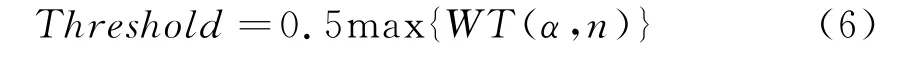
选取好合适的等高线阈值后,其等高线时频图如图2所示。

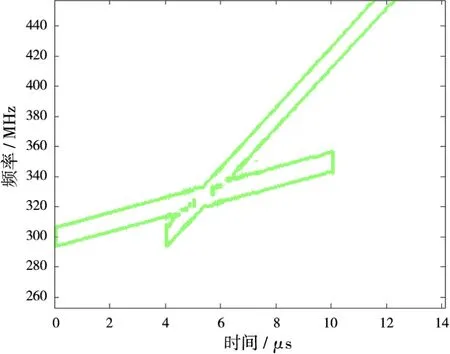
图2 混叠信号的时频等高线图

采用图像处理中的二值化思想,对时频变换数据WT(α,n)进行处理。如果WT(α,n)＞Threshold,则WT(α,n)=1;如果WT(α,n)＜Threshold,则WT(α,n)=0。作如上处理后得到一个新的时频二值矩阵,时频矩阵的二值化简化了数据处理的计算复杂度。

1.3.2 到达时间(T OA)估计

根据二值化后的时频数据,实现对混叠脉冲的到达时间进行分离。对于一个混叠的脉冲来说,其起始时刻和终止时刻的估计比较常规,也比较简单。如果满足

则WT(α,i)所对应的时刻t i即为起始时刻。同理,如果

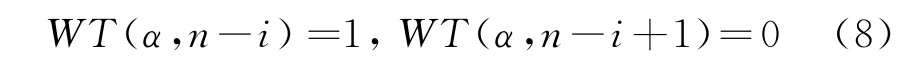
则WT(α,n-i)所对应的时刻t n-i即为终止时刻。但是要估计出由于混叠而造成脉冲丢失的起始时刻,按照这种方法并不能准确地检测并估计出其到达时间。本文提出频率位置差值法实现对混叠丢失信号的起始时刻估计。

由上述时频数据二值法可以得到WT(α,n)=1时频率所在位置α的值。由于本文根据能较好反映出信号特性以及受噪声影响小两个因素选取等高线阈值,故α的个数大于等于1。针对WT(α,n)=1处的α值,可以得到频率位置差值定义为

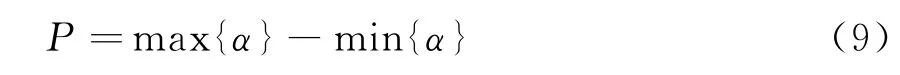
当第一次出现

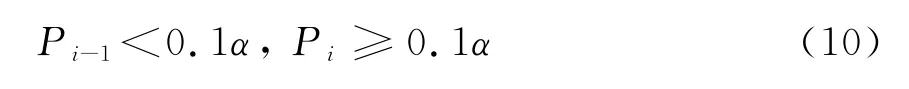
P i为第i个点时的频率位置差值,则WT(α,i)所对应的时刻t i为丢失脉冲的起始时刻。同理,当第一次出现

则WT(α,n-i)所对应的时刻t n-i为丢失脉冲的终止时刻。

估计出混叠信号各个脉冲的起始时刻和终止时刻就得到了脉冲的到达时间,利用PRI变换法对具有不同PRI的LFM雷达信号实现分选。

2 PRI变换法

2.1 PRI变换法原理

PRI变换法[5-7]是在周期信号自相关函数的基础上发展而来,为了解决自相关运算带来的子谐波,即PRI整数倍处出现峰值的问题。PRI变换法在信号自相关函数的基础上引入一个相位因子,几乎完全抑制了子谐波的出现,通过设置相应的门限,准确检测出超过门限的PRI值进行序列搜索,最终完成分选。

PRI变换法是将到达时间(T OA)作为每个脉冲的唯一变量,脉冲的TOA以脉冲的前沿时间为基准,设t n,n=0,1,2,…,N-1为脉冲估计的到达时间,N为采样脉冲数,则采样脉冲串模型化为单位冲激函数的和:

D(τ)表征了一种PRI谱图,在真实PRI处将出现峰值。PRI变换得到的D(τ)与信号自相关函数的区别在于前者引入一个相位因子exp[2πit n/(t n-t m)]。由于对信号作自相关运算,不仅仅在真实PRI处出现峰值,而且在PRI整数倍的地方也会出现峰值,出现谐波的现象;PRI变换由于引入相位因子,几乎完全抑制了子谐波的影响,能够准确地在真实PRI值处出现峰值。

2.2 检测门限

在一定的门限准则下,对PRI变换得到的D(τ)进行处理,得到真实的PRI值,根据得到的PRI值实现雷达信号的分选。其门限选择依据一般有观察时间原则、消除子谐波原则、消除噪声原则三种。

观察时间原则、消除子谐波原则都是基于真实脉冲个数的基础上而提出的。在整个采样时间T内,如果一列雷达脉冲信号的PRI为τk,则脉冲的个数为T/τk;由PRI变换原理可得知,|D(τ)|的涵义是指当前PRI脉冲信号的脉冲个数,因此,在理想情况下,|D(τ)|=T/τk。现实情况中,由于在采样时间T内,各列脉冲串不会同时出现,会有部分脉冲序列的脉冲丢失。同时由于子谐波的存在,会造成真实PRI值判断模糊。所以设定一定比例的脉冲数目为门限来判定脉冲串的存在与否(α为可调参数):

为了消除噪声对PRI变换影响,真实PRI值对应的PRI箱内的累计值必须大于噪声。因此,噪声消除原则表示如下:式中:γ为可调参数,一般γ≥3;ρ为脉冲密度;b k为第k个PRI箱的密度。

综合上述3种门限选取原则,可以设置门限为

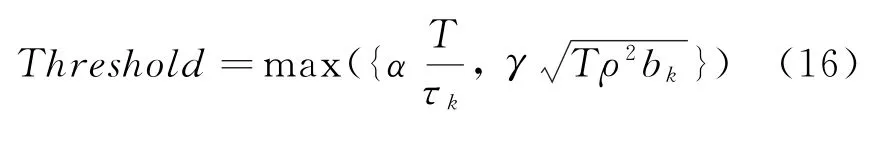
3 信号分选流程

综上所述,对于接收到的LFM雷达信号分选步骤为:

Step 1:运用式(2)～(5)对接收到的LFM雷达信号进行小波变换;

Step 2:采用式(6)截取等高线对时频等高线图进行二值化处理;

Step 3:运用式(7)、式(11)估计出丢失脉冲的起始时刻和终止时刻;

Step 4:得到所有脉冲序列的起始时刻,包括因混叠造成的丢失脉冲的起始时刻后,运用PRI变换法实现混叠LFM雷达信号的分选工作。

4 实验仿真结果

为了验证提出方法的有效性,本文采用5部LFM雷达辐射源信号作为分析对象。5部雷达共同的参数有:信号的采样率为1 GHz/s,带宽B为200 MHz,载频为300 MHz;其不同的参数有调制斜率k分别为10×1012,5×1012,20×1012,30× 1012和10×1012Hz/s;各部LFM雷达信号的起始时刻点分别为0,19,16,53和5μs;各部LFM雷达信号的脉冲重复间隔PRI分别为1,1.34,0.5, 1.77和2 ms;各部雷达的脉宽分别为10,8,15,12和10μs。5部LFM雷达信号分别产生100个脉冲信号,信噪比SNR为10 dB。

图3显示的是采用PRI变换法分别对原始混叠信号以及采用本文算法对混叠脉冲进行分离后的分选效果。PRI的门限可调值取0.6。图3(a)为直接对混叠脉冲信号进行PRI变换分选,从图中可以看出,由于信号混叠比较严重,造成丢失脉冲比较多,脉冲信息丢失的也随之增多,在一定的检测阈值下,只能分选出4种PRI的LFM雷达信号;图3(b)为经过本文算法对混叠雷达信号进行处理后的分选结果,其分选结果显示运用本文算法并结合PRI变换法能够正确地检测出不同LFM雷达信号的PRI值,进而检测出各部LFM雷达信号。由此得知,本文算法能够有效地恢复丢失脉冲的信息,恢复由于脉冲密度密集而造成脉冲混叠信号的到达时间。与传统的基于PRI变换法进行雷达信号分选相比,本文算法具有更佳的分选效果。

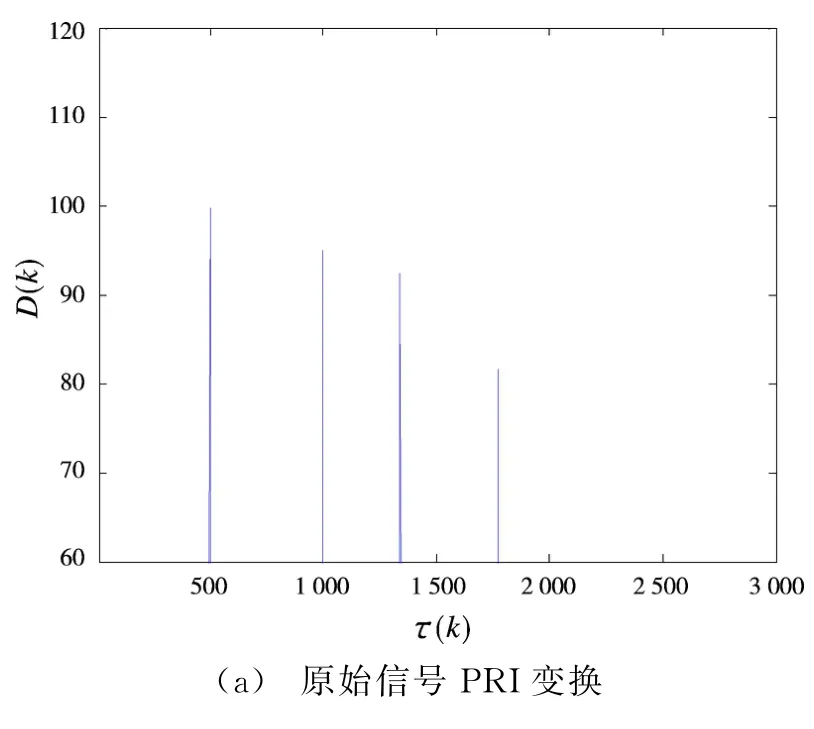
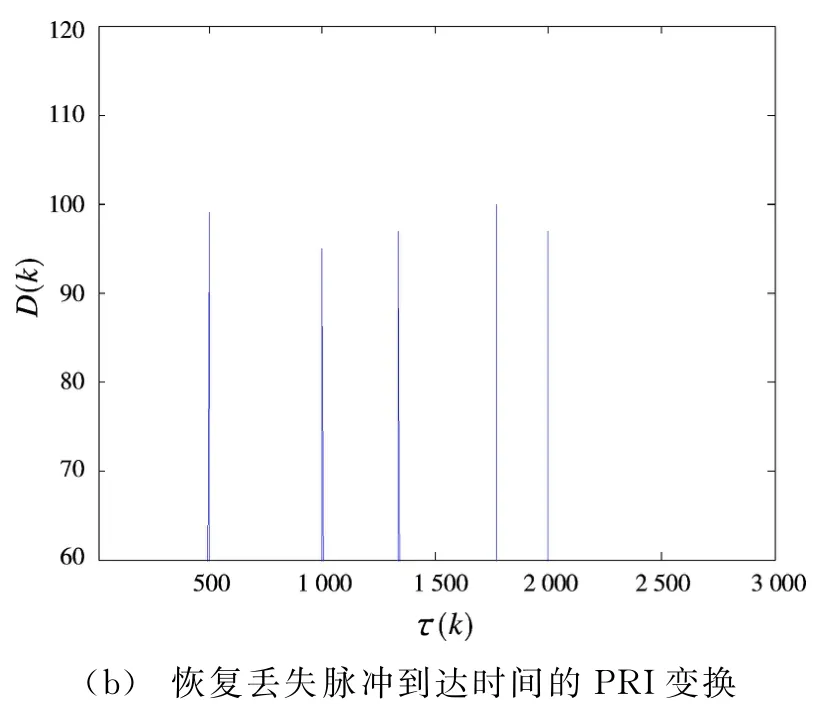
图3 原始信号和恢复丢失脉冲后基于PRI变换的分选效果

表1给出的是本文算法检测出的PRI值与真实值的比较结果。从表中可以看出,本文算法不仅能够完整地检测出各部LFM雷达信号的PRI值,而且其估计值和真实值的整体误差在1%左右。其结果表明,在一定的信噪比情况下,本文算法能够较准确地检测出各部LFM雷达信号的PRI值,具有一定的工程应用价值。

表1 估计PRI值和真实PRI值的比较和误差

5 结束语

雷达信号分选作为电子侦察的重要组成部分,其分选效果的好快直接主导着战争的结果。LFM信号由于采用脉冲压缩技术,被广泛应用于雷达中,故LFM雷达信号分选在当今雷达分选中有着相当大的研究意义。现代战争复杂的电磁环境造成雷达脉冲流密集且混叠较严重,针对雷达脉冲混叠而造成部分雷达脉冲信息丢失而影响雷达分选性能的问题,本文提出一种恢复因混叠而丢失的脉冲信息,还原各个雷达脉冲的到达时间(TOA),进而采用传统的PRI变换法进行LFM雷达信号分选。实验仿真结果表明,在一定的信噪比条件下,本文算法通过恢复丢失脉冲信息,能够检测出每部LFM雷达的PRI值,并且估计误差基本维持在1%左右,具有一定的工程应用价值。

[1]李益民,王丰华,黄知涛,等.反辐射导引头抗非相干三点源性能分析[J].系统工程与电子技术,2011,33 (3):500-505.

[2]康乃馨,何明浩,王冰切,等.基于压缩感知的多径LFM信号参数估计[J].雷达科学与技术,2016,14 (3):291-296. KANG Naixin,HE Minghao,WANG Bingqie,et al. Parameter Estimation of Multipath LFM Signal Based on Compressive Sensing[J].Radar Science and Technology,2016,14(3):291-296.(in Chinese)

[3]乔宏乐,王超,王鹏.基于PRI变换法的脉冲信号分选算法[J].火控雷达技术,2012,41(2):34-38.

[4]陈晓军,成昊,唐斌.基于ICA的雷达信号欠定盲分离算法[J].电子与信息学报,2010,32(4):919-924.

[5]童姗,张冰,朱志宇.基于FastICA算法和小波变换的雷达信号分选[J].现代电子技术,2013,36(19): 5-8.

[6]李一兵,葛娟,林云.基于熵特征和支持向量机的调制识别方法[J].系统工程与电子技术,2012,34(8): 1691-1695.

[7]黄宇,刘锋,王泽众,等.基于周期FRFT的多分量LFMCW雷达信号分离[J].航空学报,2013,34(4): 846-854.