基于M估计的抗野值单站无源定位方法∗
(火箭军工程大学,陕西西安710025)
0 引言
单站无源定位技术[1-2]是指利用一个观测平台上的单个或多个接收机,通过被动接收目标辐射源的辐射信息来对其进行定位和跟踪的技术,具有电磁隐蔽性好、设备相对独立、作用距离远和易于工程实现等优点。现有的单站无源定位方法主要有测向定位法、到达时间定位法、多普勒频率定位法、方位/到达时间定位法、相位差变化率定位法和多普勒频率变化率定位法等,用到的滤波算法主要有扩展卡尔曼滤波(Extended Kalman Filter,EKF)[3-4]、无迹卡尔曼滤波(Unscented Kalman Filter,UKF)[5-6]和容积卡尔曼滤波(Cubature Kalman Filter,CKF)[7-8]等。杨晓君等[9]在EKF算法的基础上,提出了基于相位差、相位差变化率和频率变化率的单站无源定位方法(PFRC),该方法具有较高的定位精度和较快的收敛速度。
上述大多数方法都是建立在观测信息准确的基础上。然而,在实际问题中,由于测量设备本身出现故障或者环境干扰、目标机动等的影响,观测数据不可避免会出现野值。统计学家根据大量数据指出,在生产实际和科学实验中,野值的出现约占观测总数的1%~10%[10]。野值的出现使得观测数据的可靠性和可用性下降,降低了定位精度,甚至无法定位。
目前,已有大量文献对野值存在时如何保持估计量的最优性进行了论述,但有关单站无源定位跟踪问题的研究中,涉及野值处理问题的文献较少。例如,文献[5,11-13]研究了野值存在时如何辨识并剔除的方法;文献[6,14-16]指出,错误的观测量主要通过新息对滤波精度产生影响,因而对新息进行修正能较好地保持滤波精度;文献[17]将野值剔除法与新息修正法相结合达到抗野值效果;文献[7,18]基于Bayes定理并结合归一化受污染正态模型,根据野值出现的后验概率来自适应调整新息的方差阵,以降低野值的影响。本文在单站无源定位PFRC方法基础上,提出了一种基于 M估计的抗野值单站无源定位方法,该方法通过建立新息的非线性函数作为权函数,对新息进行权值修正,较好地消除了野值分量的影响。
1 单站无源定位方法
1.1 单站无源定位模型
单站无源定位系统的状态方程和观测方程可表示为

式中:k是时刻;X(k+1)是目标状态向量,包含目标的位置、速度等信息;Z(k+1)是包含噪声的观测向量;f和h分别是非线性状态函数和非线性测量函数;D(k)是激励矩阵;U(k)为未知加速度;W(k+1)和V(k+1)分别是过程噪声和测量噪声,彼此独立且服从Gauss分布,它们的协方差矩阵分别为Q(k+1)和R(k+1)。
在PFRC方法中,测量向量包括相位差、相位差变化率、频率变化率。因此,非线性测量函数可表示为

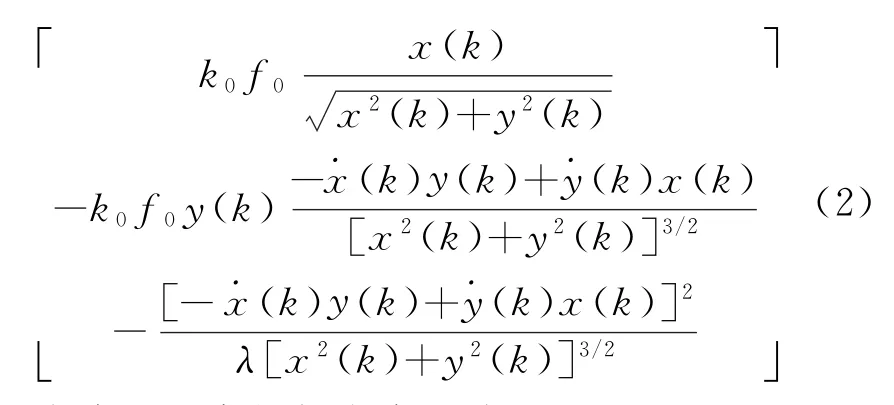
滤波过程中的新息定义为
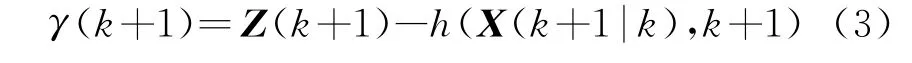
它隐含了当前最新观测值Z(k+1)的信息,是实际观测值与预测值(拟合值)之间的差,故又称为残差序列。
1.2 野值的影响分析
在单站无源定位理想模型中,当滤波达到稳态时,新息γ(k+1)应为零均值的独立正态同分布随机序列,在这种情况下,卡尔曼滤波器对状态的估计值可以达到很高的精度。但实际情况中,观测数据不可避免会出现野值。不妨假设k时刻出现野值,并把野值看作叠加于正常观测数据上的一个冲击分量,则观测方程变为

式中,Z(k+1)′为叠加野值分量后的观测值,B为冲击形式的野值分量。
则加入野值后得到的新息序列为

由此可见,野值分量的影响主要体现在新息序列上。在野值分量出现的时刻必须采取适当的措施对新息序列进行校正,才能消除野值对估值精度的影响。
在观测值中,野值的表现形式主要有以下两种[5]:
1)孤立型野值,表现为k时刻的观测数据为野值时,在k的某一个领域内的其他观测数据是正常的,即野值的出现是孤立的。
2)斑点型野值,表现为k,k+1,k+2,…,k+p时刻的观测值均严重偏离真值,即野值成片出现。
常用的野值处理方法有直接剔除法和新息修正法。直接剔除法能较彻底地消除野值分量的不良影响,但当大量孤立型野值出现,或者大片斑点型野值出现时,直接剔除受野值污染的观测值会导致数据缺失严重,仍然会降低定位精度,甚至使滤波器发散。而仅对新息进行平滑修正,虽能保留观测序列的完整性,但当野值分量值较大时,难以消除野值的不良影响。本文采用基于M估计法对新息进行权值修正,在考虑野值分量水平的情况下,将观测值分为正常观测值、不正常但可以利用观测值,以及不可利用观测值这三类,既能保留可利用的观测值,又可以较彻底地消除野值分量的影响。
2 M估计在单站无源定位中的应用
2.1 M估计的定义
抗差估计[19]或称稳健估计是指在粗差不可避免的情况下,选择适当的估计方法使估计量尽可能减少粗差的影响,得出正常模式下的最佳估值。抗差估计包括M估计、L估计和R估计。其中, M估计是经典的极大似然估计的推广,称为广义极大似然型估计。
传统的极大似然估计(MLE),其估计量T n= T n(x1,x2,…,x n)需满足

式中,f是随机变量(x1,x2,…,x n)的概率密度。
1964年Huber用函数ρ代替式(6)中的-lnf(·)使其广义化:

式中,ρ(·)称为极值函数。假设ρ(·)的导数为是待估参数,它包括定位参数和尺度参数,于是式(7)可以写为

式(7)和式(8)均可用于定义M估计,当ψ函数是ρ函数的导数时,式(7)和式(8)定义的M估计等价。
常用的ρ函数是对称的、凸的或在正半轴上非降的函数,而ψ函数常取成这种ρ函数的导数。当然,ψ函数也可根据需要适当选取。有一个ρ(或ψ)函数就定义一个M估计,因此M估计实际上是一类估计,故称为广义极大似然型估计。显然,经典的极大似然估计是M估计的特例。
2.2 单站无源定位中的M估计

式中,ρ(·)表示适当选择的凸函数,n表示观测向量维数,γ(k)i表示时刻k新息序列的第i个元素。式(8)定义的M估计则可表示为
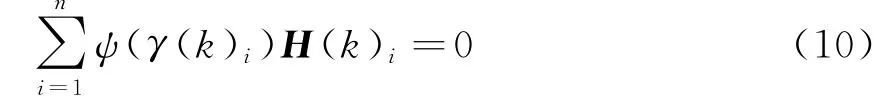
式中:ψ(·)也是适当选择的单调、正半轴非降函数;H(k)i是测量函数h(X(k),k)的偏导矩阵H(k)的第i行向量。令
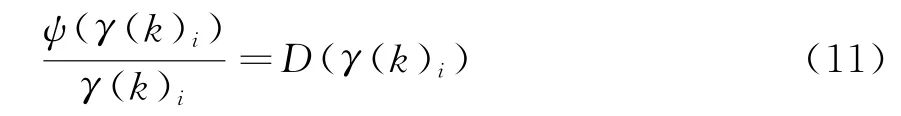
则式(10)可写成

式中,D(γ(k)i)可看成权函数。式(12)写成矩阵形式为
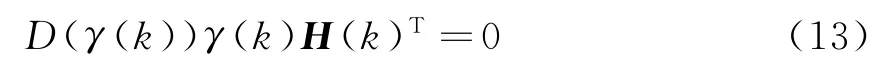
式中,D(γ(k))=diag[D(γ(k)1),D(γ(k)2),…,D(γ(k)n)]。
从式(11)可以看出,权函数D(γ(k)i)是新息序列的非线性函数。所以,M估计的实质是用权函数去修正新息原有的权,它实现抗差化的基本思想是:
1)对于正常观测值采取保权处理,即令D(γ(k)i)=1,此时,M估计退化为最小二乘估计。
2)对于非正常但又可以利用的观测值采取降权处理,即令D(γ(k)i)<1。
3)对于野值超过一定范围的、不可用的观测值,使其权为0,予以淘汰,即令D(γ(k)i)=0。
因此,抗差化的关键就在于建立恰当的权函数。本文中,权函数D(γ(k)i)由IGG法[19]确定:
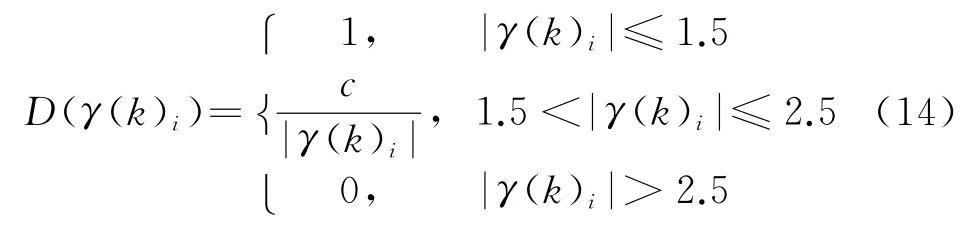
式中,c为一选定的常数。
2.3 基于M估计的单站无源定位方法
本文在文献[9]提出的PFRC方法基础上,通过建立新息的非线性函数作为权函数,对新息序列进行权值修正,实现了PFRC算法的抗野值能力。基于M估计的单站无源定位方法步骤如下:
1)时间更新
① 设定初始值
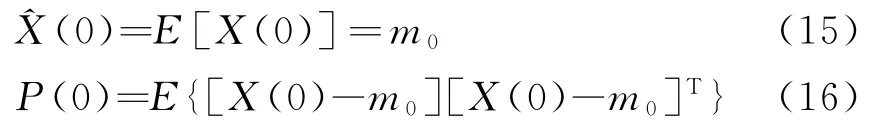
② 一步预测

③ 一步预测均方误差

④ 滤波增益
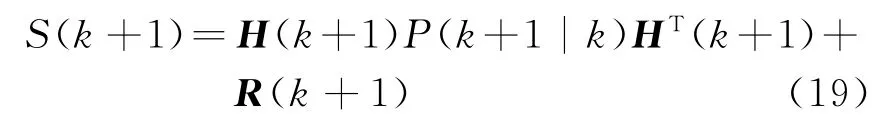
2)测量更新
① 计算测量新息
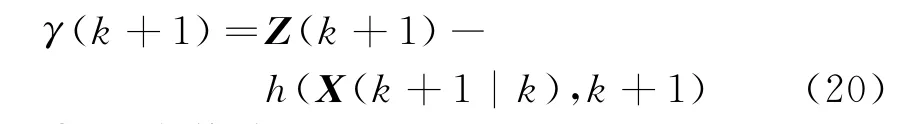
② 状态估计
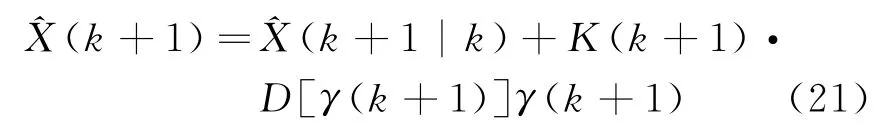
③ 估计均方误差
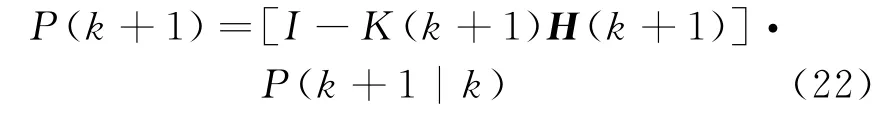
3 仿真实验
为了检验基于M估计的单站无源定位方法的抗野值能力,通过改变野值的水平和式(14)中常数c的值,分别针对孤立型野值和斑点型野值进行Monte-Carlo仿真实验。
不失一般性,仿真以二维单站无源定位情况为例,假设固定观测站位于坐标原点,目标辐射源作匀速直线运动,观测周期为Ts=1 ms,取1 500个观测点,初始状态X(0)=[200 m,549 m,-300 m/s,0 m/s],在观测时间内目标辐射源的频率保持f=200 M Hz不变。
本文采用相对定位误差(RPE)和相对速度误差(RVE)来描述单站无源定位的性能,其定义为

3.1 孤立型野值仿真实验
选取不同的常数c值,在第600个观测时刻,对相位差观测量添加大小不同的野值。图1和图2分别展示了c=0.1和c=1.5的情况下,野值的大小为B=2和B=10时的仿真结果。
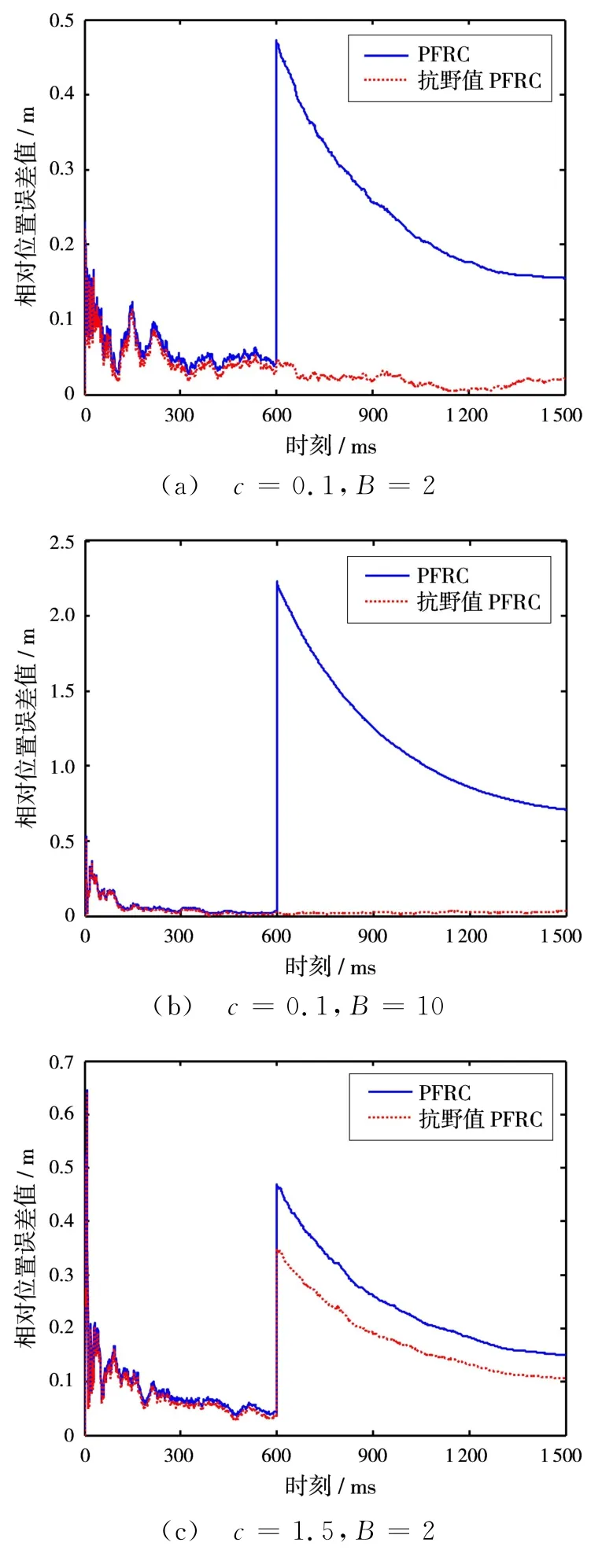
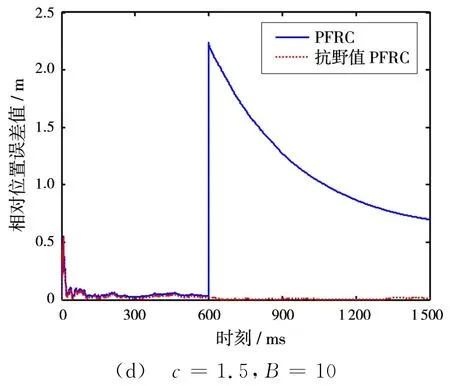
图1 基于100次Monte-Carlo实验的相对位置误差值
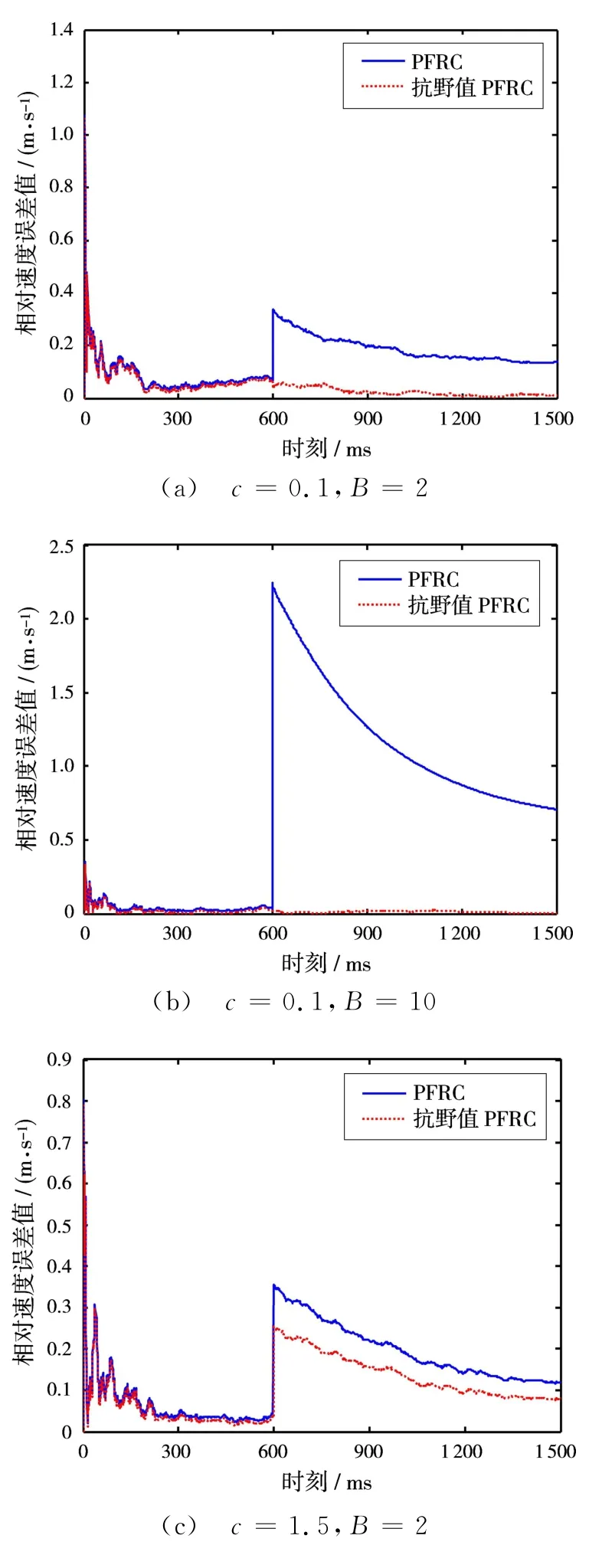
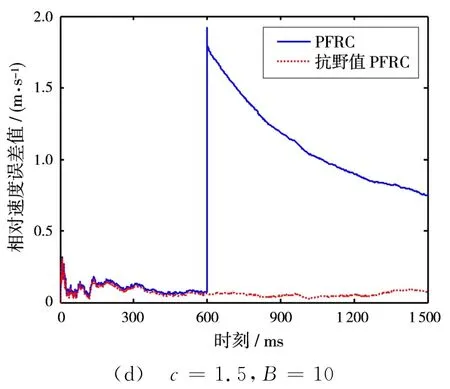
图2 基于100次Monte-Carlo实验的相对速度误差值
通过图1和图2可以看出:
1)当观测量中未出现野值时,两种算法的定位精度一样。
2)当观测量中存在单个野值的时候,PFRC方法的定位精度受到了比较严重的影响,这是由于观测新息突然增大,导致滤波增益也随之变大,使得估计结果较大地偏离了真实值;而基于M估计的抗野值PFRC方法,能根据新息变化自适应地调整权函数值,通过对新息的权值修正克服野值分量的影响。
3)当常数c取值越小时,抗野值PFRC方法的稳定性就越好,滤波系统也收敛得更快,表现出了较强的鲁棒性。
4)当野值分量越大时,抗野值PFRC方法的优越性体现得越明显。
3.2 斑点型野值仿真实验
选取常数c=0.1,从第600个观测时刻开始,连续添加大小为B=2的野值分量。图3和图4分别展示了连续5个时刻、10个时刻添加野值时的仿真结果。
通过图3和图4可以看出,当观测量连续出现野值时,PFRC方法的滤波精度受到很大影响,甚至导致滤波器发散;而基于 M 估计的抗野值PFRC方法保持了较好的稳定性,滤波器依旧可以收敛到正常状态,具有较强的鲁棒性。
4 结束语
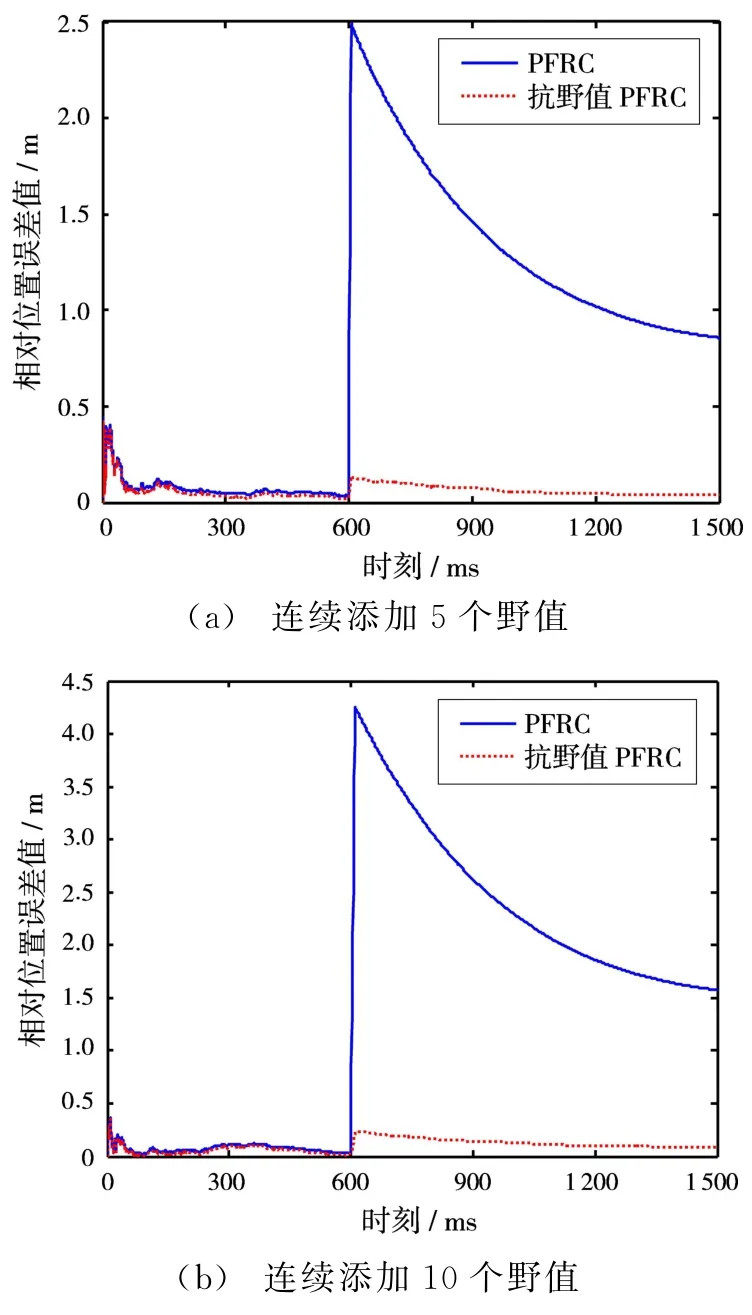
图3 基于100次Monte-Carlo实验的相对位置误差值
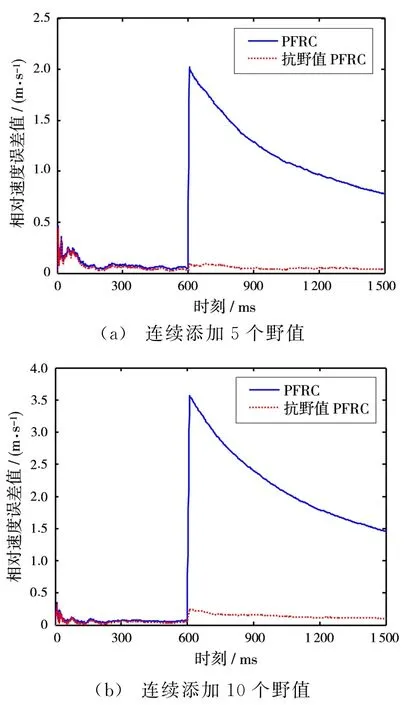
图4 基于100次Monte-Carlo实验的相对速度误差值
在实际情况中,单站无源定位过程中出现野值是不可避免的,野值的存在会影响定位的精度和系统的稳定性,以致严重失真和误判。本文通过建立新息的非线性函数作为权函数,对新息进行自适应权值修正,提出了一种新的基于M估计的抗野值单站无源定位方法。通过对孤立型野值和斑点型野值进行仿真实验,结果表明,本文的算法能很好地克服野值影响,具有较强的鲁棒性和较高的定位精度。并且当不存在野值时,该算法能保持原PFRC算法的精度。
以往在单站无源定位研究中,考虑到野值问题的文献较少,本文所提方法较好地解决了单站无源定位中的野值问题,具有一定的实用性。
[1]孙仲康,郭福成,冯道旺,等.单站无源定位跟踪技术[M].北京:国防工业出版社,2008.
[2]杨晓君,陆芳,郭金库,等.模糊单站无源定位方法[J].清华大学学报(自然科学版),2011,51(1):25-29.
[3]李炳荣,丁善荣,马强.扩展卡尔曼滤波在无源定位中的应用研究[J].中国电子科学研究院学报,2011,6 (6):622-625.
[4]孟祥飞.基于扩展卡尔曼滤波算法的无源定位效果分析[J].电子科技,2012,25(3):25-27.
[5]张怡,廉晶晶,黄文刚.抗野值性能的无迹卡尔曼滤波算法的研究[J].计算机工程与应用,2012,48(33): 153-156.
[6]张学峰,周超,刘文超.抗野值滑动平均-UKF算法在组合导航中的应用[J].数字技术与应用,2015(2): 133-134.
[7]霍光,李冬海,李晶.单站无源定位中的抗野值鲁棒CKF算法[J].雷达科学与技术,2013,11(4):419-423. HUO Guang,LI Donghai,LI Jing.An Outlier Rejecting Robust CKF Algorithm for Single Observer Passive Location[J].Radar Science and Technology, 2013,11(4):419-423.(in Chinese)
[8]霍光,李冬海.基于后向平滑容积卡尔曼滤波的单站无源定位算法[J].信号处理,2013,29(1):68-74.
[9]YANG X,LIU G,GUO J.A Single Observation Passive Location Algorithm Based on Phase-Difference and Doppler Frequency Rate of Change[C]∥2008 IEEE International Conference on Systems,Man and Cybernetics,Budapest,Hungary:IEEE,2008: 1309-1313.
[10]HUBER P J.Robust Statistics[M].New York:Wiley,1981.
[11]杨军玲.无源定位跟踪中野值的检测与剔除方法[J].电子科技,2016,29(6):51-53.
[12]卢元磊,何佳洲,安瑾.目标预测中的野值剔除方法研究[J].计算机与数字工程,2013,41(5):722-725.
[13]张强,孙红胜,胡泽明.目标跟踪中野值的判别与剔除方法[J].太赫兹科学与电子信息学报,2014,12 (2):256-259.
[14]武昱,曹鑫,钱克昌,等.一种鲁棒的Kalman滤波方法[J].计算机与数字工程,2013,41(5):716-718.
[15]戴文舒,陈新华,孙长瑜,等.等价权修正的Kalman抗野值滤波算法[J].应用声学,2013(5):409-412.
[16]朱占龙,单友东,杨翼,等.基于新息正交性自适应滤波的惯性/地磁组合导航方法[J].中国惯性技术学报,2015,23(1):66-70.
[17]李广军,李忠,崔继仁.新型抗野值的Kalman滤波器研究[J].计算机应用与软件,2013,30(1):136-138.
[18]贾浩正.抗野值的航迹数据Kalman滤波[J].测控技术,2014,33(9):26-28.
[19]周江文,黄幼才,杨元喜,等.抗差最小二乘法[M].武汉:华中理工大学出版社,1997.

