基于遗传算法的MIMO-SAR面阵优化∗

(电子科技大学电子工程学院,四川成都611731)

0 引言

MIMO-SAR(Multi-Input Multi-Output-SAR),即“将相参MIMO雷达置于运动平台之上,综合利用全部收发组合的回波数据进行相参成像”。MIMO-SAR雷达发射和接收天线合理的布阵设计能够提高系统性能、降低硬件成本,决定着MIMO-SAR成像模式、处理方法等。

常见的MIMO-SAR阵列可以分为:方位向一维线阵、距离向一维线阵、高度向一维线阵及混合阵四种类型[1-2]。MIMO-SAR天线一维线阵优化及天线综合理论已经获得了广泛而深入的研究,但这种MIMO-SAR一维线阵天线在很多实际场合中都存在局限性[2-3],尤其是较低的系统实时性。二维平面阵天线的MIMO-SAR由于在沿航迹方向和切航迹方向均布设天线阵元,满足三维雷达成像所必须的平面阵元,在不到一个合成孔径时间甚至几个脉冲重复时间内就可以获得高分辨率的雷达图像,从而确保了成像的实时性。因此,研究MIMO-SAR二维平面阵的布阵方式成为阵列构型设计的新课题。MIMO-SAR由于雷达平台处于运动之中,存在运动误差和平台抖动等问题,在优化过程中可以采用等效阵元的方式处理。在优化方法的选择上,遗传算法非常适用于非线性的优化问题,所以用于解决稀疏的一维线阵优化布阵问题已进行过不少的研究[4-9]。然而遗传算法可能会产生种群单调及早熟收敛,使得优化问题无法达到最优解[10]。

本文针对机载MIMO-SAR平面阵天线阵元优化问题,在发射接收天线孔径长度、最小阵元间距和阵元数目固定等约束条件下,以降低等效收发天线方向图旁瓣电平和主瓣宽度为优化目标,基于PCA原理建立了天线平面阵优化模型,提出了一种变异率和交叉率可调的改进遗传算法实现对平面收发阵元位置的优化。最后,设计了30发30收平面天线阵元构型,仿真结果表明了该平面阵元设计的有效性与优越性。

1 基于PCA原理的MIMO-SAR天线平面阵优化模型

对于机载的MIMO-SAR系统,阵列天线满足远场条件,可用PCA原理(发射和接收分置的天线阵元,可以由位于它们中心位置的一个收发共用的相位中心等效[6-7])将实际的M个发射阵元N个接收阵元等效为M×N个收发共用的阵元,克服分置天线建立天线方向图的困难。

图1中所示为M×N的平面阵,选取阵列左上角阵元为基准点,某平面波信号s(t)以入射方向(θ,φ)到达天线阵元,其中θ和φ分别表示入射信号的俯仰角和方位角。则信号入射到第k个阵元上引起与参考阵元间的时延[4,10]为

式中,(xk,yk,0)为第k个阵元在空间中的位置坐标,c为光速。

当每个等效阵元权值都有ωk=1时,由时延τk可得水平放置的阵列方向图为

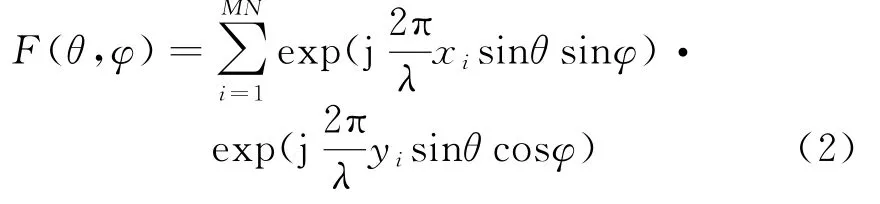
式中,(xi,yi,0)为第i个阵元的位置坐标,λ为入射波形的波长。由式(2)可知,平面阵的方向图是关于俯仰角与方位角的二元函数。

图1 等效虚拟阵元平面结构

设散射点在该坐标系下的俯仰角为θ0,目标方位角为φ0,根据式(2)得到MN个等效阵元面阵的方向图[7]为

天线阵列方向图的峰值旁瓣比、主瓣宽度关系到MIMO-SAR成像的优劣,一般来说,高的峰值旁瓣比与窄的主瓣宽度可以得到聚焦效果好的雷达图像。因此,雷达天线阵列的优化目的就是得到高的峰值旁瓣比与窄的主瓣宽度。

设机载MIMO-SAR天线发射阵元个数为M,接收阵元数目为N,雷达发射波长为λ,阵列布阵范围为L×H的矩形平面,满足远场条件。根据式(3)以峰值旁瓣比倒数与主瓣宽度最小为优化目标,建立雷达面阵的一种优化模型为

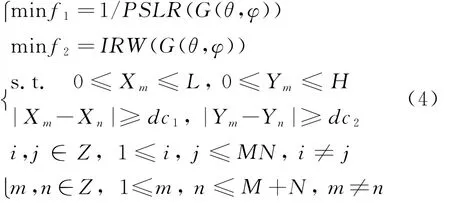
式中,PSLR为天线方向图的峰值旁瓣比,IRW为方向图的主瓣宽度,(xi,yi,0)为第i个等效虚拟阵元的位置坐标,(Xm,Ym,0)为实际发射或接收阵元位置坐标,dc1为实际收发阵元横坐标最小间隔,dc2为实际收发阵元纵坐标最小间隔。

式(4)中峰值旁瓣比PSLR是指式(3)中等效阵元方向图主瓣高度与最大旁瓣比,以分贝(dB)表示;主瓣宽度IRW是指归一化后的方向图主瓣在3 dB的脉冲宽度。

2 基于遗传算法的MIMO-SAR天线平面阵优化

由式(4)的模型可知,优化过程中,由于发射阵列和接收阵列的位置不定,且各阵元间隔不等,因此,该雷达的阵列优化问题是一个多重非线性全局优化问题。遗传算法(GA)与随机搜索和模拟退火等全局优化方法相比,不仅优化效率高,而且收敛速度快得多[6]。GA优化中,从一群试验解(个体)中选出一些较优的解,在适应度函数的选择压力之下朝最优解进化,而不是随机地在解空间中产生解,因此遗传算法具有更快的收敛速度[10]。与此同时,GA算法利用变异和交叉操作,不断产生新解,又在一定程度上保证了解的随机性。可以说GA算法折中了随机搜索法的鲁棒性和局部最优化技术的快速收敛特性[5,10]。遗传算法作为一种搜索工具和优化方法,在阵列天线设计等电磁学问题中得到广泛应用。虽然遗传算法具有较强的全局搜索能力,但是同时杂交选择使得部分适应度低的个体失去了遗传进化的机会,这实际上降低了GA的多样性,可能会引起早熟提前收敛,无法获得最优解。本文的多约束稀布阵优化是基于一种改进的遗传算法,可以有效地遏制算法的早熟。

2.1 平面阵元初始位置编码

GA求解的问题为雷达天线实际N收M发阵元的位置坐标,编码采用实数编码的方式。在阵列的优化模型式(4)中,由于任意两个阵元位置坐标的间隔满足|Xm-Xn|≥dc1,|Ym-Yn|≥dc2,m≠n,这里dc1和dc2由工程人员实际给出,因此在编码的过程中,将整个布阵范围L等分为间隔为dc1的小段,将H等分为间隔为dc2的小段,对每一小段的端点横纵坐标进行实数编码。这样,将每个实际N收M发阵元位置取值在等分小段的端点上,保证了阵元之间的最小间隔。同时,为了保证MN个等效虚拟阵列的长度,以得到雷达成像高分辨率,将矩形布阵范围的4个端点固定布设2发2收阵元,如图2所示。

图2 MIMO-SAR天线收发阵元位置示意图

图2 中,黑色圆点表示接收阵元,黑色方框表示发射阵元,横虚线之间的间距为dc2,竖虚线之间的间距为dc1,可见各阵元之间满足最小间距的约束。

2.2 适应度函数及阵元选择操作

由式(4)可知,阵列优化模型是一个含有两个优化目标的多目标非线性优化问题。对于该问题常采用权重系数变换法,取f1与f2的优化权重系数都为1,则评价阵元位置优劣的适应度函数可由阵列方向图的峰值旁瓣比和主瓣宽度一起构成:

式中,XT,YT,XR,YR分别是发射阵元和接收阵元的横纵坐标,G(θ,φ)maxsl为归一化后虚拟等效阵元天线方向图的第一旁瓣峰值,Δφ0.5,Δθ0.5分别为方位向和俯仰向主瓣半波功率宽度,归一化的天线方向图G(θ,φ)由实际发射和接收阵元位置决定。本文以最大旁瓣电平和主瓣宽度之和为遗传算法的优化函数,这里的适应度函数值为负。

本文采用遗传算法中常见的轮盘赌选择法,所有的选择是从当前种群(全部收发阵元组成的阵列群)中根据个体的适应度值与整个种群中个体(单个阵元位置)适应度函数值的比例,适应度绝对值高的被选中的可能性就越大。群体中旁瓣水平好并且主瓣窄的个体被选择的概率高;而旁瓣水平较差或主瓣宽的个体被选择的概率就低。

2.3 阵元位置交叉和变异操作

交叉和变异操作是遗传算法的核心,同时也是产生新的阵元位置的主要手段。交叉又称重组,是按较大的概率从阵列群中选择两个阵元,交换编码后的两个阵元的某个或某些码位。GA算法的交叉主要有单点交叉、两点交叉和多点交叉。遗传算法也引入了变异算子来产生新的阵元位置,遗传算法中所谓的变异运算是指,将编码后的单个阵元上的某个或某些码位用其他阵元的相应码位替换,从而形成一个新的阵元个体。

因此,交叉概率Pc和变异概率Pm的选择对于整个算法的运算效率及收敛性有很大的影响。标准的遗传算法中,交叉概率和变异概率都是常数,当算法进入局部收敛的时候,按照不变的交叉和变异概率,有时候很难跳出局部解,所得解的方差较小,产生早熟提前收敛现象,从而无法获得最优的阵元位置。本文提出了一种交叉率和变异率可变的计算公式,可以在一定程度上遏制这种早熟现象。

本文引入早熟的标志量δ,假设第i次迭代过程中,种群中最优个体适应度函数为fopt(i),所有个体适应度均值为

式中,f(n,i)为第i次迭代种群中第n个个体的适应度值,K为种群规模,G为迭代次数。将所有个体适应度大于fav(i)的个体再次求均值得到f av′(i)。令

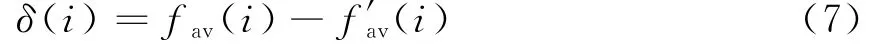
当种群的适应度方差减小即δ(i)增大时,迭代有可能进入到局部最优,发生早熟现象。现将交叉率和变异率设为δ(i)的函数,所设计的概率应为δ(i)的增函数,即随着种群有可能进入早熟,加大交叉和变异概率产生更多新解,使其跳出早熟。因此,交叉概率Pc和变异概率Pm可以进行如下设计:

式中:k1和k2属于0到1间的数,一般说来,交叉概率较大而变异概率较小,因此给定参考值k1=0.2,k2=0.1;w1和w2为调整权值,用于调整指数项的权重,给定参考值w1=1,w2=2。这些参数的参考值,只是根据多次仿真实验经验所得,对于具体的优化问题还需要依据目标函数值进行多次调整,以得到最佳结果。

2.4 平面阵元优化模型求解步骤

基于改进的遗传算法收发阵元位置优化流程如下:

(1)给定种群(收发阵列群)规模K,进化迭代次数G,根据本文的初始阵元编码方式建立初始的收发阵列群;

(2)计算阵列群的适应度值,计算阵元位置交叉概率Pc和阵元位置变异概率Pm;

(3)判断优化准则(适应度函数的门限值,可跟实际情况设定)是否满足,若已满足则转向第(6)步,否则继续;

(4)选择优势个体(适应度函数值高的阵元位置),进行交叉和变异操作;

(5)计算更新后的阵列群的适应度函数值,判断连续10次迭代的适应度值是否不变,若不变则转向第(6)步,否则转向第(4)步;

(6)输出最佳的收发阵元位置,阵列优化过程结束。

具体流程图如图3所示。

图3 改进遗传算法流程图

3 仿真实验分析

仿真采用矩形的平面稀布布阵方式,发射阵元数M=30,接收阵元数N=30,机载MIMO-SAR工作载频为fc=10 GHz,布阵范围为L=99.5λ,H=99.5λ,阵元间最小间隔dc1=雷达采用前视的工作方式,假设前视角为45°,目标的波达方向θ0=45°,φ0=60°,利用遗传算法求解阵列优化模型。

本文先采用标准的遗传算法优化阵列,然后采用本文中所述的改进遗传算法进行阵列优化,比较两种算法的优劣。

标准的遗传算法基本参数为:初始种群数为100,选择概率为0.9,交叉概率为0.8,变异概率为0.01,终止代数为200。

本文改进遗传算法的基本参数为:初始种群数为100,选择概率为0.9,交叉变异概率参数k1=0.2,k2=0.1,w1=2,w2=2,终止代数为200。

图4为采用标准的遗传算法和文中改进遗传算法分别进行优化布阵过程中适应度函数收敛曲线。

图4 适应度函数收敛曲线

由图4可见,标准的遗传算法结果种群收敛至-19.014 8 dB,而采用文中改进之后的遗传算法优化结果收敛至-20.419 8 d B。在第60代时,采用标准的遗传算法优化结果陷入早熟,而改进的遗传算法可以跳出早熟,寻找更优解。这说明这种改进方法是可行的并且能够有效防止种群早熟收敛。

采用文中改进遗传算法得到优化后的30收30发阵元位置如图5所示。

图5中,黑点表示发射阵元的位置,星点表示接收阵元的位置。从图5可以看出,阵元是稀布的,阵元间距满足最小间隔0.015 m的要求,并且布阵范围4个顶点分布着2发2收阵元,以得到最长的等效阵列。

利用PCA原理得到的等效虚拟30×30收发共用阵元位置如图6所示。

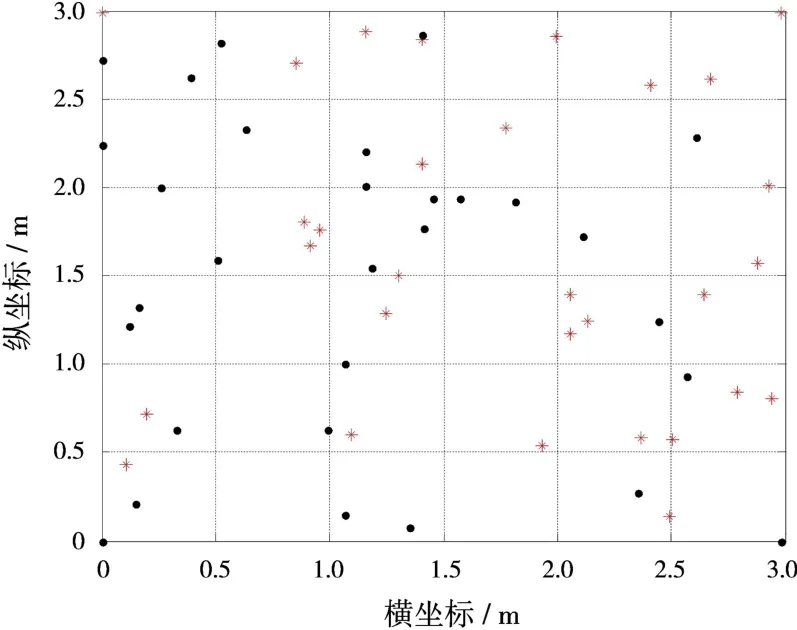
图5 优化后发射和接收阵元位置

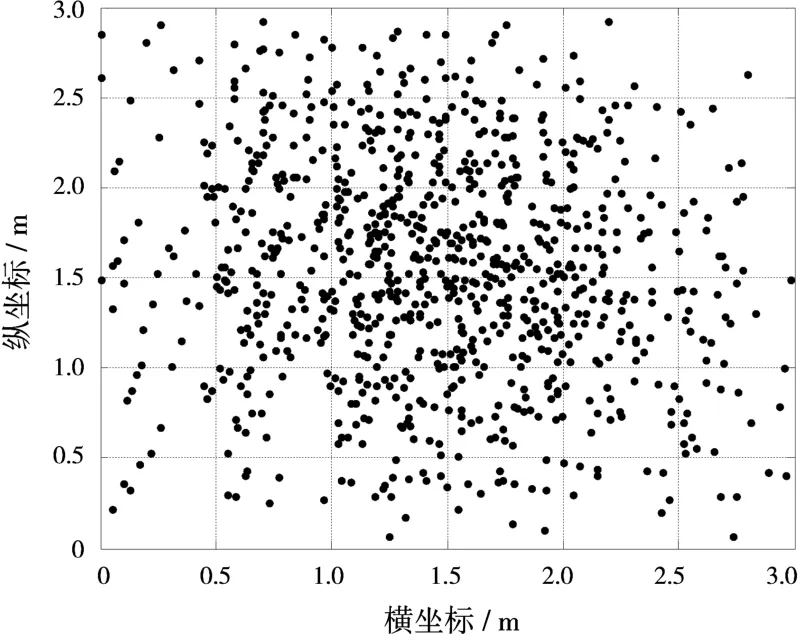
图6 等效虚拟收发共用阵元位置

经过文中改进遗传算法优化后的等效虚拟阵元收发天线方向图如图7所示。

由图7(a)可见,由俯仰向看去最优布阵可以将峰值旁瓣比控制在-20.29 dB,主瓣宽度为0.8°;由图7(b)可见,由方位向看去最优布阵可以将峰值旁瓣比控制在-21.23 dB,主瓣宽度为0.9°。将方位向和俯仰向方向图联合求平均,得到优化后的稀布平面阵主瓣为0.85°,峰值旁瓣比为-20.76 d B。

为了比较所提此种平面布阵方式的优劣,本文根据MIMO-SAR线阵常见布阵方式[3],扩展出了MIMO-SAR平面阵的几种布阵方式,并分析了各种阵列方式的优劣。本文扩展出的4种布阵阵型(布阵范围均为仿真实验所述的L×H)如下:

(1)利用本文方法得到的等效阵元数目为900的稀布平面阵A;

(3)等效阵元数目为900,阵元位置10次随机分布中最优的平面阵C;

(4)等效阵元数目为900,阵元间隔为2λ的均匀稀疏平面阵D。

不同的平面阵布阵方式的天线方向图如图8所示,不同布阵方式所得到的最优峰值旁瓣比与主瓣宽度如表1所示。

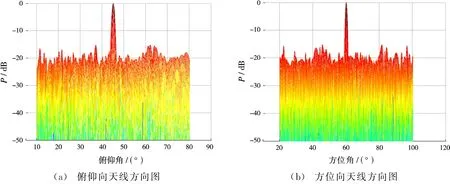
图7 改进遗传算法优化后的等效阵列方向图

联合图7、图8和表1可以看出,布阵形式A可以得到很好的峰值旁瓣比和主瓣水平,并且无栅瓣;相较于满阵形式B,采用布阵A的方式可以节省更多的阵元,节省了成本,提高了效率;相较于布阵C,采用布阵A的方式可以得到更好的旁瓣和主瓣;相较于布阵D,采用布阵A的方式可以获得更低的旁瓣水平,并且无栅瓣。此种比较结果同时表明本文所提改进的遗传算法进行MIMO-SAR平面阵优化的可行性与有效性。

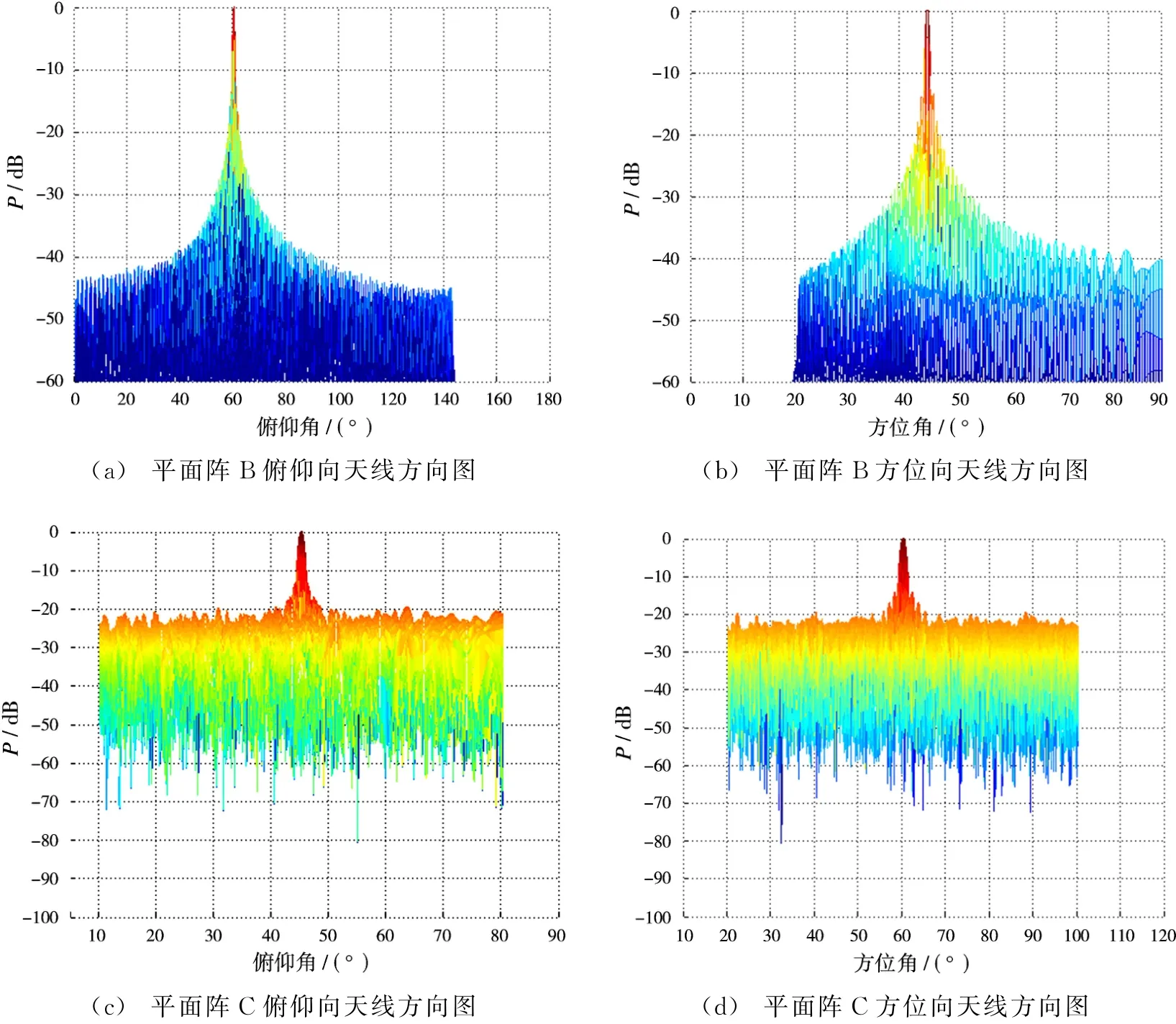
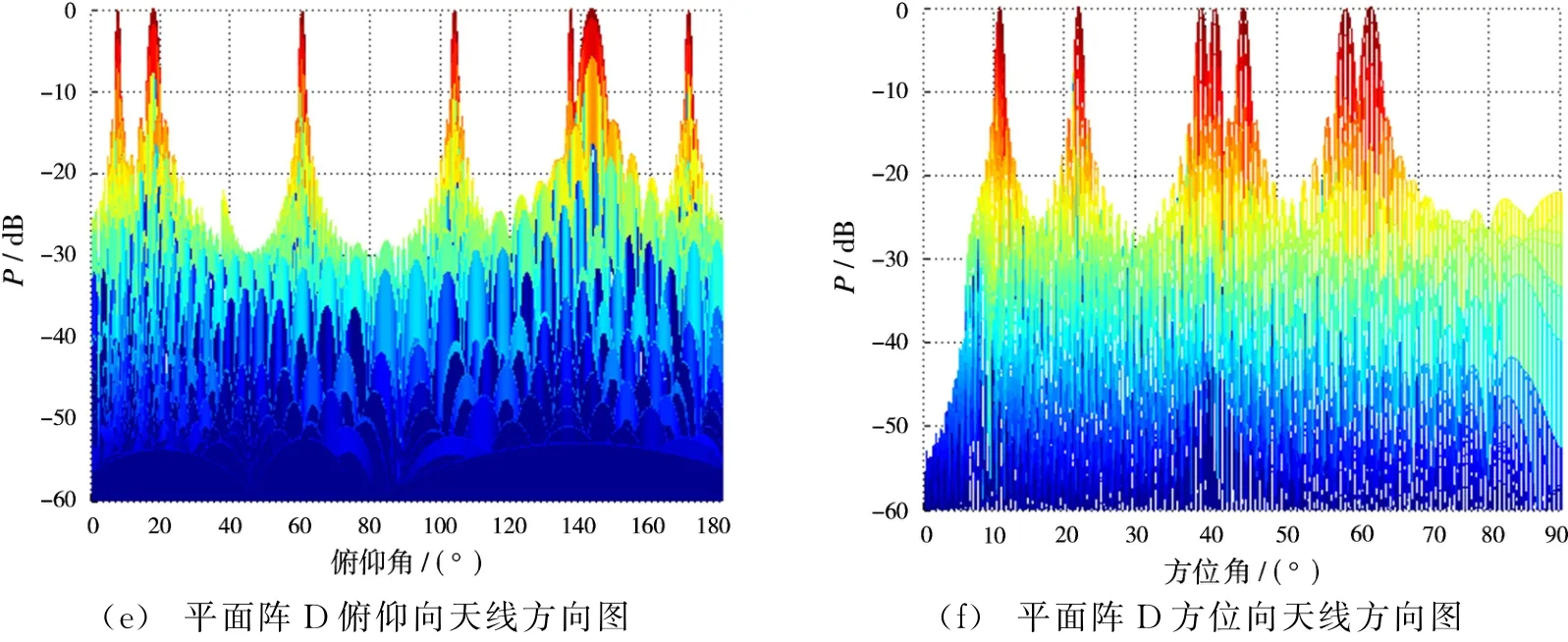
图8 各种布阵方式阵列方向图比较

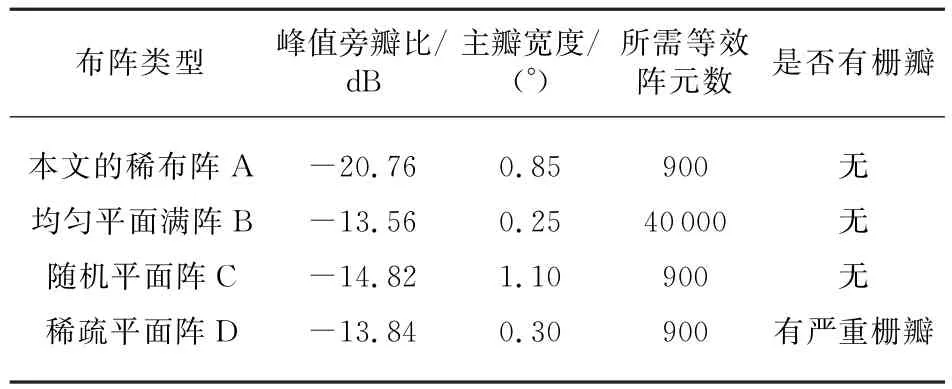
表1 不同布阵方式的旁瓣与主瓣值

4 结束语

MIMO-SAR系统的平面阵优化要同时考虑发射、接收阵列对合成等效虚拟阵列的影响,且实际工程设计中,在一定约束条件下,要保证天线阵列低的旁瓣电平和窄的主瓣宽度;另一方面,在阵列优化模型求解中,传统的遗传算法局部搜索能力差,可能早熟收敛。针对上述问题,本文基于天线相位中心近似原理建立了一种阵列方向图的优化模型;提出了一种变异率和交叉率可调的遗传算法,可以有效地防止早熟收敛;在目前常见线阵布阵方式的基础之上,扩展了几种MIMO-SAR平面阵的布阵方式,并与本文布阵方式进行对比。结果表明,此种改进的遗传方法可以在阵元数、最小阵元间距给定,以及布阵范围给定的情况下,得到较窄的主瓣及较好的旁瓣水平,为MIMO-SAR三维成像及目标检测与识别提供方便。同时,采用这种阵元最小间距约束的稀布平面阵形式,需要的阵元数目大大减少,从而有效地降低了天线系统的成本与计算量,更适合工程设计的需要。

[1]WANG W Q,CAI J Y.Ground Moving Target Indication by MIMO SAR with Multi-Antenna in Azimuth[C]∥IEEE International Geoscience and Remote Sensing Symposium,Vancouver,BC:IEEE,2011:1662-1665.

[2]周伟,刘永祥,黎湘,等.MIMO-SAR技术发展概况及应用浅析[J].雷达学报,2014,3(1):10-15.

[3]MOREIRA A,PRATS-IRAOLA P,YOUNIS M,et al.A Tutorial on Synthetic Aperture Radar[J].IEEE Geoscience and Remote Sensing Magazine,2013,1(1):6-43.

[4]AHMAD F,AMIN M G,YOON Y S.Multi-Input Multi-Output Synthetic Aperture Radar Technology for Urban Area Surveillance[C]∥3rd International Asia-Pacific Conference on Synthetic Aperture Radar,Seoul:IEEE,2011:1-4.

[5]和洁,冯大政,李晓明.基于多重混合遗传算法的MIMO雷达天线布阵优化[J].微波学报,2010,26(4):55-60.

[6]方红.基于遗传算法的MIMO发射接收阵列联合优化研究[J].计算机工程与设计,2013,34(5):1812-1816.

[7]陈客松,何子述.平面稀布天线阵列的优化算法[J].电波科学学报,2009,24(2):193-198,205.

[8]和洁,冯大政,孟超,等.采用遗传算法的MIMO雷达L型阵列稀布优化[J].电讯技术,2015,55(8):872-878.

[9]赵振波,张刚,李相平.基于遗传算法的弹载SAR弹道优化设计[J].雷达科学与技术,2012,10(3):257-261.

ZH AO Zhenbo,ZH ANG Gang,LI Xiangping.Trajectory Design and Optimization for Missile-Borne SAR Based on Genetic Algorithm[J].Radar Science and Technology,2012,10(3):257-261.(in Chinese)

[10]王小平,曹立明.遗传算法:理论、应用与软件实现[M].西安:西安交通大学出版社,2002:108-109.