单/双基地雷达超低空探测研究∗
(军械工程学院电子与光学工程系,河北石家庄050003)
0 引言
近年来,随着空战装备技术的发展和空袭战术的改进,现代战场上巡航导弹、武装直升机等超低空(高度在10~300 m之间)目标越来越多。这些目标飞行高度低、航线隐蔽,在地球曲率和地形起伏的遮挡,以及强地杂波的掩盖下非常难以被发现。超低空突防在实施对敌打击时的优势在近几十年的多次战争中被广泛应用,对战场要地防空提出了新的考验[1]。
双基地雷达由于收发分置,在对低空目标探测时具有单基地雷达无法比拟的优点[2-3]。根据Babinet原理,目标的前向散射雷达截面积(Radar Cross Section,RCS)与目标的表面形状和涂覆材料无关,而完全由入射场和目标的轮廓决定,当双基地角到达180°时,目标的RCS达到最大值。因此,双基地雷达对低空目标的探测优势主要是利用目标的前向散射区。然而,随着双基地角的增大,目标的距离估计精度会迅速降低,当双基地角接近180°时,双基地雷达基本丧失对目标的定位能力,可以认为是无效的探测区域。文献[4-5]分析了双基地雷达对金属椭球体的低空探测能力。文献[6]基于经验公式分析了双基地雷达对隐身目标的探测范围。文献[7-9]对临近空间双基地雷达的探测范围进行了分析,这种配置下超低空区域的双基地角相对较小,不利于对超低空目标的探测,同时在临近空间配置大功率的发射机会有极大的成本和被发现的概率。文献[10-11]分别对压制干扰下的空地双基地雷达探测范围和基于旋翼无人机的空地双基地雷达的空间同步进行了研究。以上文献均没有考虑双基地角临近180°时的无效探测区域,双基地低空探测分析并不完善。
本文仿真分析了距离探测精度随双基地角的变化关系,综合考虑了双基地角临近180°的无效探测区域,以及目标位于不同双基地角下的RCS等因素,对单基地雷达、地基双基地雷达和空地双基地雷达在超低空区域对巡航导弹等弱目标的探测能力进行了对比分析。结果表明,地基双基地雷达的探测盲区主要分布在超低空区域,而空地双基地雷达将探测盲区转移到了低空和中低空区域,对超低空弱目标的探测能力远大于单基地雷达和地基双基地雷达,用空地双基地雷达作为现役单基地雷达的超低空补盲雷达有极大的应用价值。
1 单/双基地雷达探测范围分析
1.1 单基地雷达探测范围分析
在不考虑方向图传播因子的情况下,单基地雷达方程为

式中:Gt为发射天线增益,Gr为接收天线增益,对于单基地雷达,通常Gt=Gr;σ(αT)为与波束入射角相关的目标雷达截面积函数,αT为入射波束与水平面的夹角;Ls为损耗因子,Ls>1;Pt为发射的峰值功率;PRmin为接收的最小可检测信号功率。

式中:M为脉冲积累个数,当使用单个脉冲回波进行检测时M=1;Pcr为宽带接收机的脉冲压缩比,Pcr=Pw×Bn(即时宽带宽积);k为玻耳兹曼常数,k=1.38×10-23J/K;T0为标准室温,一般取290 K;Bn为接收机的噪声带宽,一般由中放决定。
由式(1)可得,不同距离下单基地雷达接收到的信号能量为
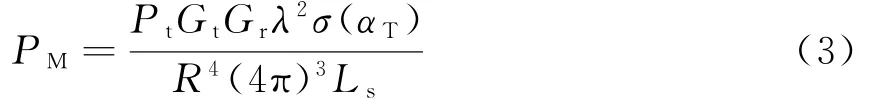
雷达若能发现目标,需要满足

1.2 双基地雷达探测范围分析
在不考虑方向图传播因子的情况下,双基地雷达的雷达方程不同于单基地雷达,为
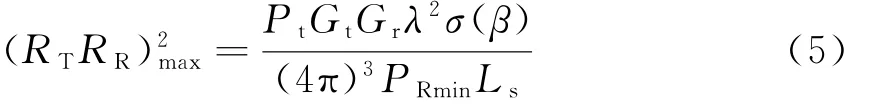
式中,RT为目标到发射机的距离,RR为目标到接收机的距离,σB(β)为与双基地角相关的目标雷达截面积函数,其他参数定义与单基地雷达方程相同。
由式(5)可得,不同双基距离积下接收机收到的信号功率为

若双基地雷达接收机的最小可检测功率与单基地雷达相同,则双基地雷达发现目标需满足

为分析单/双基地雷达在不同高度下的探测范围,以单基地雷达为原点建立XOZ二维直角坐标。X轴表示地面,Z轴表示与地面的高度,对第一象限内的整个区域进行网格划分,dx表示X轴的划分间隔,dz表示Z轴划分间隔,如图1所示。
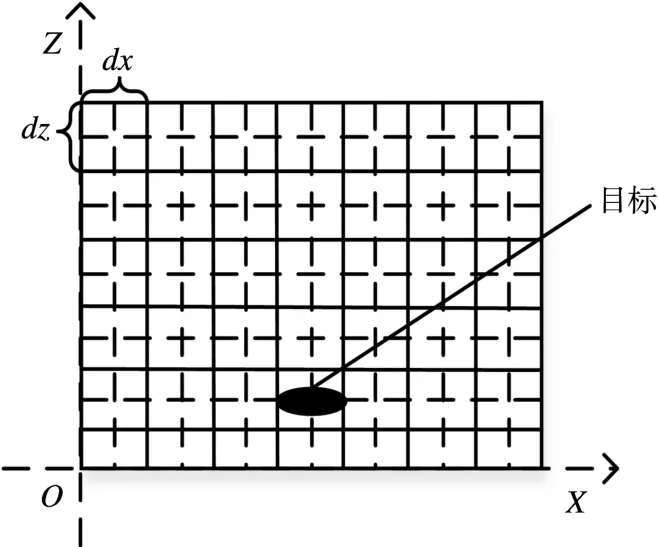
图1 探测空域网格划分
单基地雷达部署在(0,0)位置,则任意位置的目标(xi,zi)到雷达距离为

对于空地双基地雷达,发射机部署在(H,0)位置,接收机部署在(L0,0)位置,基线距离L=,可得
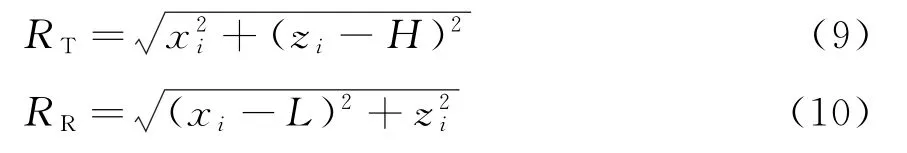
分析单/双基地雷达的探测范围时,根据式(4)和式(7)计算图1中划分的每个网格中心点处的目标是否可以被检测到。若能被检测到,则认为整个网格内的区域均为可探测范围,令发射机的高度H=0即可得到地基双基地雷达的探测范围。
2 目标的单/双基地雷达截面积分析
进行超低空突防的目标主要为巡航导弹,为了便于分析,以细长金属椭球体的RCS来近似替代巡航导弹的RCS,一般巡航导弹的尺寸远大于雷达发射电磁波的波长,在不考虑表面涂覆材料的影响时,导弹的RCS一般处于光学区。椭球体处于不同位置时,其相对于雷达的视线角是变化的,记水平放置的椭球体的视线角与水平面的夹角为α,用标准物理光学近似法来分析细长金属椭球体的单基地RCS如下[12]:
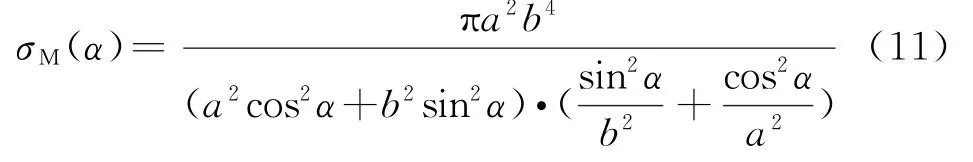
式中,a为椭球体的长轴长,b为短轴长。
文献[6]通过分析得出了双基地雷达截面积与单基地雷达截面积的经验公式,为
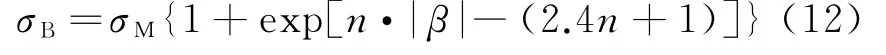
式中:σB为双基地雷达截面积;σM为单基地雷达截面积;n为经验参数,一般取7~10;β为双基地角,单位为rad。
椭球体尺寸a=5 m,b=0.5 m,根据式(11)和式(12),图2(a)给出了该椭球体不同入射角下的单基地RCS,图2(b)给出了入射角为30°,n=8情况下,该椭球体不同双基地角下的RCS。从图2(b)可以看出,在双基地角大于135°时,椭球体的RCS随双基地角的增大而迅速增加。
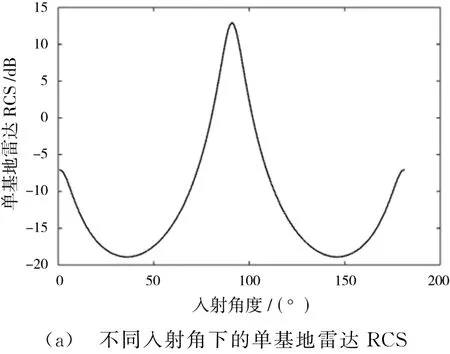
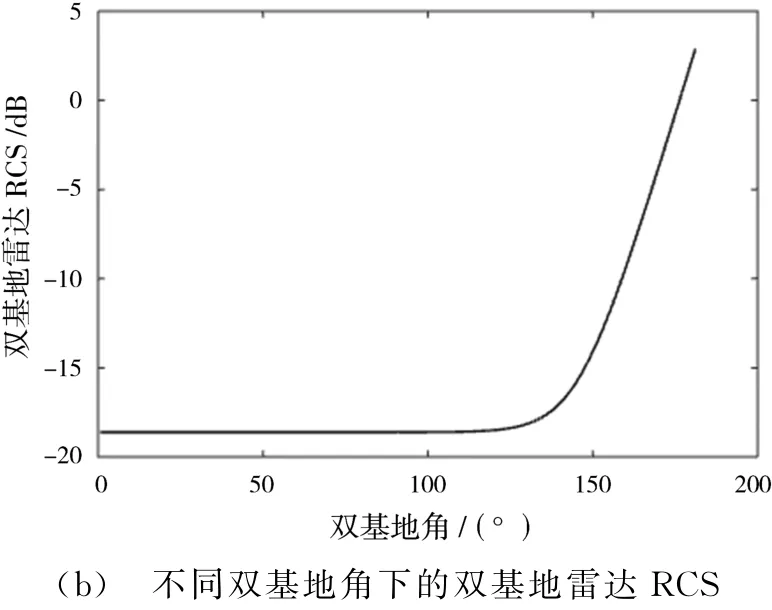
图2 单/双基地雷达RCS分布
3 距离探测精度分析
通常在双基地平面中采用距离和-角度方法进行目标测距,得到接收站到目标距离RR表达式[13]为
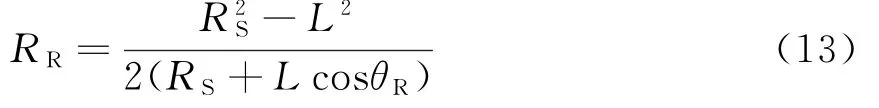
式中,RS为发射站-目标-接收站距离和,L为发射站-接收站基线长,θR为双基地平面上的目标视角。
在空地双基地雷达中,如图3所示,发射站的高度为H,其与接收站的倾角为θT,目标到发射站的距离为RT,目标到接收站的距离为RR,β为目标的双基地角,RS,θR和L的定义同式(13)。
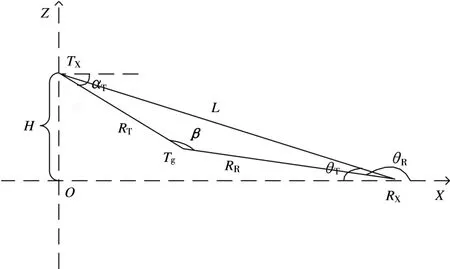
图3 空地双基地几何示意图
以接收站中心,将空地双基地配置逆时针旋转θT为地基双基地配置,根据式(13),在空地双基地雷达中,接收站到目标距离RR表达式为
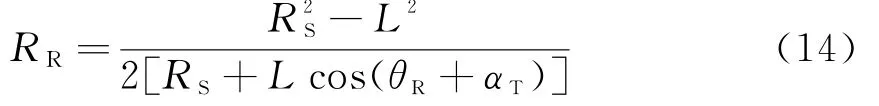
目标的双基地角

RR的测量误差主要是由Rs,θR,θT和L的测量误差导致的,根据误差理论,均方根误差表达式如式(16)所示:
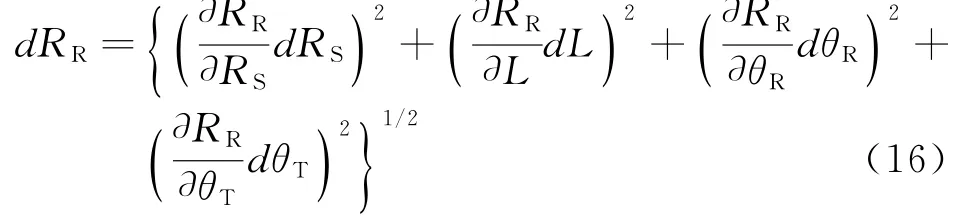
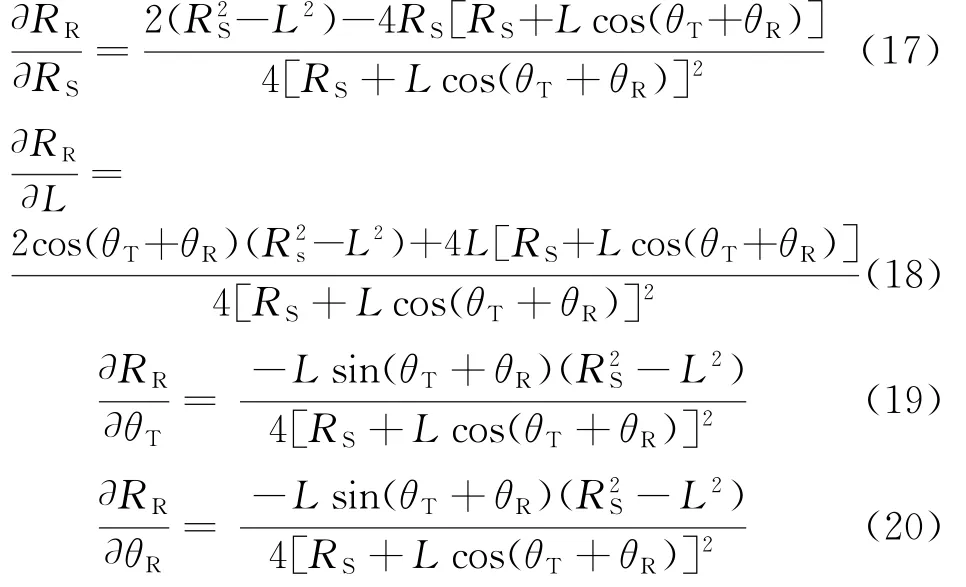
4 仿真分析
仿真1:不同配置单/双基地雷达对巡航导弹的低空探测范围分析
以长轴长5 m、短轴长0.5 m的金属椭球体目标为例进行分析,地基双基地雷达的基线距离L=20 km,空地双基地雷达发射机高度H=2 km,发射机和接收机的水平距离L=20 km。探测空域的网格划分如图2所示,dx=50 m,dz=5 m,整个空域范围的水平距离为25 km,高度为1 000 m。不同配置的雷达发射天线增益和接收天线增益均为30 dB,损耗因子为10 d B,发射机功率为100 W,脉压增益为10 dB,脉冲积累个数为10,接收机最小可检测信号功率为10-13W。根据式(4)和式(7)得不同配置单/双基地雷达对巡航导弹的探测范围,如图4所示。
从图4可以看出,双基地雷达(包括地基双基地雷达和空地双基地雷达)在对1 000 m以下的低空区域进行探测时有明显的优势,地基双基地雷达对水平距离距发射机较近的区域有更强的探测能力,但在远区低空区域,空地双基地具有和地基双基地雷达同样强的探测能力。

图4 不同配置下的单/双基地雷达对巡航导弹的探测范围
仿真2:双基地雷达距离探测精度仿真分析
双基地的距离探测精度与双基地角之间的关系与双基地配置无关,因此仿真采用的双基地雷达配置同仿真1中的地基双基地雷达,仿真时,根据式(17)和式(20)分别分析在距离和估计误差和目标角度估计误差影响下,双基地雷达距离探测误差斜率同双基地角的变化关系,如图5所示。图5(a)的误差斜率表示1 m的距离和测量误差所产生的目标距离估计误差,图5(b)的误差斜率表示0.1°的角度估计误差所产生的目标距离估计误差。
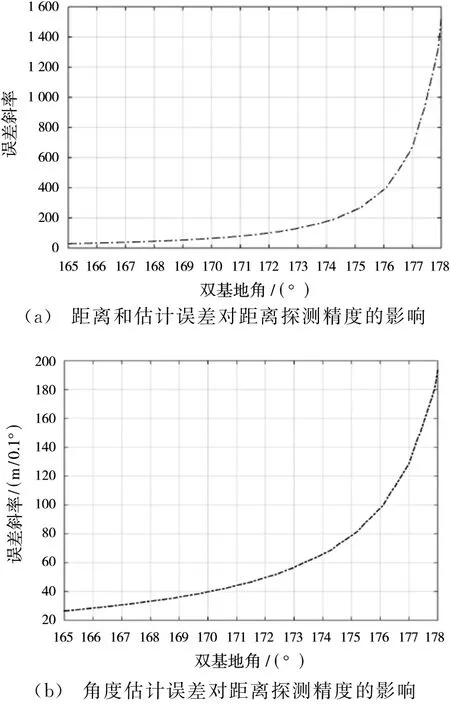
图5 双基地雷达距离探测精度与双基地角的关系
基线测量精度、距离和测量精度对双基地距离探测精度的影响是在同一数量级的且误差斜率同双基地角的变化趋势一致,因此只需分析其中一个即可。图5(a)和图5(b)表明,当双基地角大于174°时,距离和误差和角度估计误差对双基地雷达的测距误差影响成指数型增长;当双基地角大于174°时,双基地雷达几乎失去对目标的距离测量能力。因此,双基地角大于174°的区域可以认为是无效的探测区域。
仿真3:不同配置单/双基地雷达有效探测区域仿真分析
根据仿真2分析,双基地雷达的有效探测区域应为双基地角小于174°的区域且在双基地雷达的视距范围内。单/双基地雷达的配置方式同仿真1,根据式(15)计算这两种双基地配置对应的双基地角等值线,如图6所示。图7在仿真2基础上考虑了双基地雷达的探测盲区,给出了不同配置的单/双基地雷达在300 m以下超低空区域的有效探测范围。
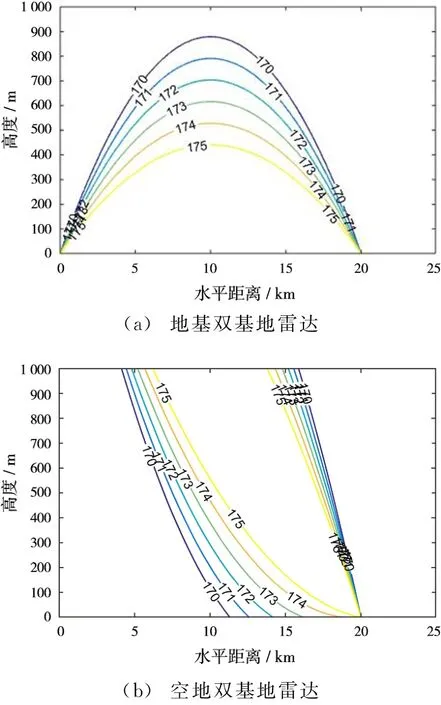
图6 双基地雷达等双基地角曲线分布
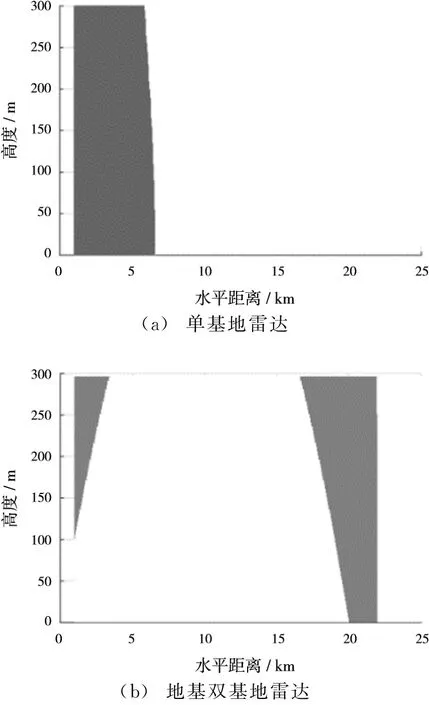
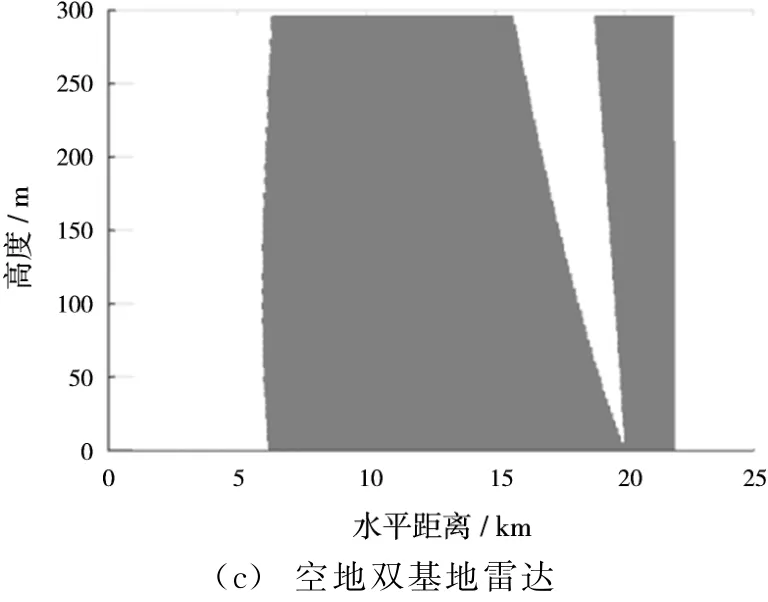
图7 不同配置单/双基地雷达有效探测区域
从图7可以看出,在相同的功率和收发天线增益条件下单基地雷达对巡航导弹的低空探测距离相对较近,普通的地基双基地雷达对300 m以下的超低空区域存在极大的盲区,在此区域内普通双基地雷达基本无法确定目标的具体位置,空地双基地雷达随着空域高度的降低有效的探测区域越来越大,因此对采用地形匹配制导的巡航导弹具有更强的探测能力。从单基地雷达和空地双基地雷达的有效探测区域来看,在接近发射机的距离空地双基地雷达存在盲区,而单基地雷达在这一区域内有较好的探测能力,因此空地双基地雷达可以作为普通单基地雷达的超低空补盲雷达,从而增大对巡航导弹等进行超低空突防目标的探测能力。
5 结束语
理论分析和仿真结果表明,弱目标在大双基地角下RCS会显著升高,双基地雷达对低空区域弱目标的探测能力要明显强于单基地雷达,然而当双基地角接近180°时,目标的距离探测精度会迅速降低。对比单基地雷达、地基双基地雷达和空地双基地雷达的有效探测区可以发现,空地双基地雷达对于低空、超低空区域探测有着普通雷达难以比拟的优势。空地双基地雷达发射平台具有较好的机动性,可根据战场需求灵活地调整空地双基地配置,从而使空地双基地雷达发挥更大的作用,下一步将对不同配置下的空地双基地雷达对超低空区域的探测范围进行研究。
[1]马井军,马维军,赵明波,等.低空/超低空突防及其雷达对抗措施[J].国防科技,2011(3):26-35.
[2]杨振起,张永顺,骆永军.双(多)基地雷达系统[M].北京:国防工业出版社,1998.
[3]李晓东.连续波扩频双/多基地雷达[J].电光系统,2000,92(2):35-39.
[4]张小宽,甄蜀春,钞刚.单/双基地雷达的低空探测性能研究[J].系统工程与电子技术,2003,25(12):1478-1480.
ZHANG Xiaokuan,ZHEN Shuchun,CHAO Gang.Research on the Low-Altitude Detection Performance of Monostatic and Bistatic Radars[J].Systems Engineering and Electronics,2003,25(12):1478-1480.(in Chinese)
[5]张小宽,甄蜀春,于庆国.双基地雷达的探测范围分析[J].弹箭与制导学报,2003,23(1):196-198.
[6]吴小坡,时家明,莫正攀,等.双基地雷达对隐身目标探测区域的计算[J].现代防御技术,2012,40(4):124-127.
[7]门向生,田新华,宫健.临近空间双基雷达探测隐身目标性能研究[J].电光与控制,2009,16(5):43-46.
[8]陈长兴,王博,牛德志,等.临近空间双基地雷达抗低空突防能力分析[J].现代电子技术,2011,34(23):1-3.
[9]王博,陈长兴,牛德智,等.临近空间双基地雷达探测性能分析[J].实验室研究与探索,2013,32(4):67-70.
[10]刘琪,孙仲康.空地双基地系统的探测范围分析[J].国防科技大学学报,1997,19(5):14-17.
[11]马彦恒,宋瑶,董健.空地双基地雷达空间同步研究[J].雷达科学与技术,2015,13(1):65-69.
MA Yanheng,SONG Yao,DONG Jian.Research on Spatial Synchronization in Air-Ground Bistatic Radar[J].Radar Science and Technology,2015,13(1):65-69.(in Chinese)
[12]郭文彦,吕长荣,张敬东.细长椭球导体雷达散射截面的分析计算[J].哈尔滨工业大学学报,1990(5):37-40.
[13]宁晋炜.双基地雷达定位精度和空间同步方法研究[D].西安:西安电子科技大学,2011.

