主动段弹道跟踪与关机点估计算法研究∗

钮俊清,任清安

(1.中国电子科技集团公司第三十八研究所,安徽合肥230088;2.孔径阵列与空间探测安徽省重点实验室,安徽合肥230088;3.智能情报处理重点实验室,安徽合肥230088)

0 引言

反导预警和防御已成为世界各国争相研究的热点,弹道导弹在主动段飞行时,由于真假弹头还未释放,多弹头还未分离,因此避开了识别真假弹头的难题,这对提高拦截成功率具有一定优势[1-3]。因此,导弹的主动段跟踪和关机点的估计在整个反导防御体系中显得至关重要。

通常针对弹道导弹主动段探测和跟踪的装备主要有反导预警卫星和前置地基雷达,而采用前置地基雷达跟踪弹道导弹主动段具有一定的战略意义,能获得较高的跟踪精度,同时也大大扩展了作战的空间[1,3]。

对于非合作目标,在无先验信息情况下对导弹主动段进行准确建模是非常困难的。文献[4]中采用了简单线性模型,而实际上导弹主动段的跟踪是典型非线性跟踪问题,线性化的误差会导致跟踪精度大幅下降。文献[3,5]提出了重力转弯模型,但不能准确地反映目标在主动段的运动特征,由于主动段受力情况非常复杂,通常无法建立精确的运动模型,这也导致跟踪的精度难以保证。文献[6]依据导弹推力主要由火箭发动机和燃料类型决定,使用导弹推力加速度模板的方法,这能体现导弹的运动特性,但基于模板的方法需要较多的先验信息,对于非合作的弹道导弹跟踪性能一般。

为解决上述问题,本文提出一种新的变结构多模型的方法用于弹道导弹主动段跟踪,该方法具有以下的优势:采用多模型的结构,更加适合复杂的主动段跟踪问题,特别是含多级助推段的导弹。采用UKF非线性滤波方法,与传统基于EKF的跟踪算法相比,它具有更好的跟踪精度。仿真结果显示本文的方法明显地提高了跟踪的精度,同时具有一定的关机点估计能力。

1 主动段跟踪模型描述

1.1 主动段运动模型

典型的弹道导弹飞行通常分为3个阶段:主动段、自由段和再入段,其中主动段运动尤为复杂,且不同弹型导弹的主动段差别较大。由于导弹的关机点时间和抛射角的不同,即使同一种导弹的飞行弹道都可能不同。通常主动段认为是从导弹离开发射台到关机点为止的一段弹道。在主动段,弹道导弹基本上都处于爬升状态,同时由于发动机和控制系统一直工作,在该段的飞行特点是:作用在导弹上的力有发动机推力、空气阻力、地球引力,以及地球自转所产生的外在力[7-9]。导弹在主动段飞行的时间一般在几十至几百秒范围内,在关机点之后进入自由段。

假定弹道导弹的位置X和速度V为

通过上述对弹道导弹的受力分析,在地心地固坐标系(ECEF)下建立弹道导弹主动段的运动方程:

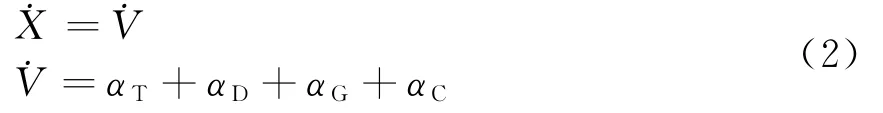
式中,弹道目标的加速度主要分为4项[2,5]:推进力αT,空气阻力αD,地心引力αG,地球自转引起的外在力αC。

1.1.1 推进力产生的加速度

弹道导弹主动段通常包含多级助推段,推进力产生的加速度可建模为

式中,αiT,Fi和Wi分别表示导弹在第i级助推段时,导弹所受推进力产生的加速度、推进力的大小和导弹整体载荷的重量。上述3个参数均为时变参数,且各级的推进力差别较大,无先验信息条件下通常很难精确建模。

导弹在关机点后进入自由段飞行,此时导弹不再受助推力的影响,即αT=0。

1.1.2 空气阻力产生的加速度

空气阻力作用于目标速度V的相反方向,其大小表示为

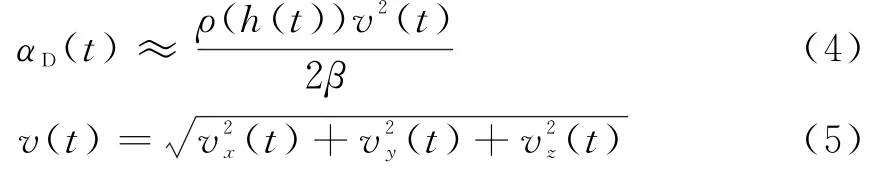
式中,v(t)为目标在时刻t时的速度,h(t)为目标在时刻t时的海拔高度。鉴于地球为不规则的椭球,目标的海拔高度需要转换到大地坐标系(WGS84)中计算,ρ(h)是空气密度函数:

式中,ρ0=1.22 kg/m3,k=0.141 41×10-3m-1。β为目标的弹道系数,近似为常量。

1.1.3 地心引力产生的加速度

地心引力从弹道目标指向地球的球体中心,一般可以忽略目标本身的质量,则依据牛顿的万有引力定律得到

式中,μG=3.985325×1014Nm2kg-1为万有引力常量,rt为在时刻t目标到地心的距离。

1.1.4 外在力产生的加速度

外在力由科氏力加速度和离心力加速度组成:

式中,¯ω为地球自转角速度矢量,¯ω=[0,0,ω]′,ω为地球自转速度。

1.1.5 弹道导弹主动段的运动模型

弹道导弹主动段的运动模型:

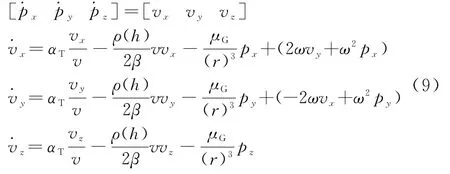
当弹道导弹在自由段飞行时,无助推力αT=0;同时,空气阻力近似为零。

1.2 地基雷达量测模型

弹道导弹防御系统中大型地基相控阵雷达的量测模型,通常在雷达阵面坐标系(RFC)下建模,如图1所示。RFC坐标系的原点为雷达阵面中心O,一般认为雷达站心重合,Z轴为阵面的法线指向,X轴为水平面与阵面的交线,Y轴沿阵面向上。A0为正北与阵面法线投影的夹角,E0为阵面法线与水平面的夹角。

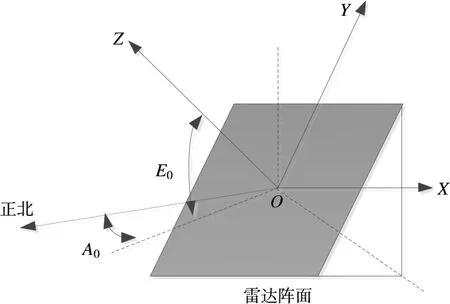
图1 雷达阵面坐标系

RFC可旋转得到雷达站心的东北天(ENU)坐标系,从ENU坐标系到RFC坐标系的转换矩阵为

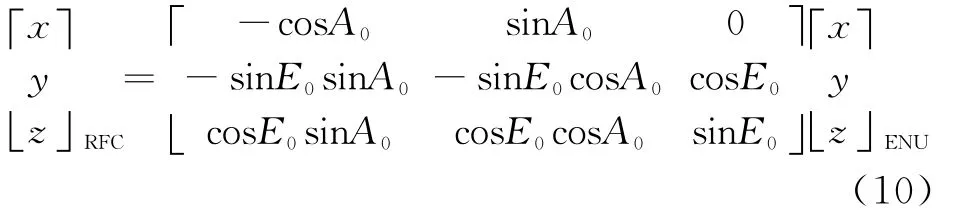
数据在以RFC的极坐标系下获得的距离r,方位α,仰角β。设[x,y,z]为RFC的直角坐标系下的 坐 标,[̇x,̇y,̇z]分 别 为 沿 各 坐 标 方 向 的 速 度 。雷达的量测模型为

式中,h(X)定义为

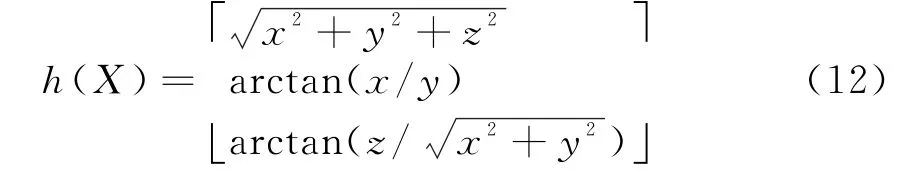
假定雷达量测数据的噪声为δ,其中距离、方位和俯仰的噪声方差分别为σr,σα和σβ。

2 主动段跟踪算法

2.1 算法描述

由于弹道导弹在主动段所受推进力的不同,典型的导弹飞行经历了一级助推段(二级和三级助推段)到自由段的过程,即在任一未知时刻它的运动模型具有不确定性[3,7]。在目标跟踪领域中多模型方法用于解决目标运动模型不确定性是最有效的方法之一[10-11]。

将导弹主动段跟踪的问题建模为一个混合估计过程,该问题描述为下列的运动方程和量测方程:

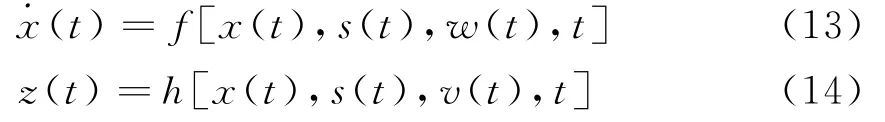
x为目标的状态,一般是连续变化的。s为系统运动模型的状态,与传统单模型目标跟踪的状态空间方程不同的是,目标当前运动模型s是不断变化的;它的变化类似于一个阶梯式的跳变的轨迹,即模型可保持不变,或跳变到其他模式。z为系统的量测。w,v分别为过程和量测噪声。目标运动模型的集合称为目标模型的空间,表示为S。将系统的运动模型s建模为一个马尔可夫链时,运动模型的转换概率矩阵可建模为

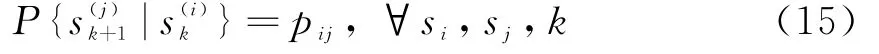
因此,本文提出了一种基于变结构多模型的弹道导弹主动段跟踪方法。该方法基于变结构模型集,模型集包含多种模型:针对主动段推进力的复杂性,设计了多个主动段的模型,将推进力大小建模为不同级别;一个自由段运动模型,其推进力大小为零(如图2所示)。鉴于弹道导弹的运动方程和量测方程均为非线性方程,从滤波性能和工程实际应用的角度综合考虑,非线性滤波算法采用性价比较高的不敏滤波(UKF)算法[12-14]。

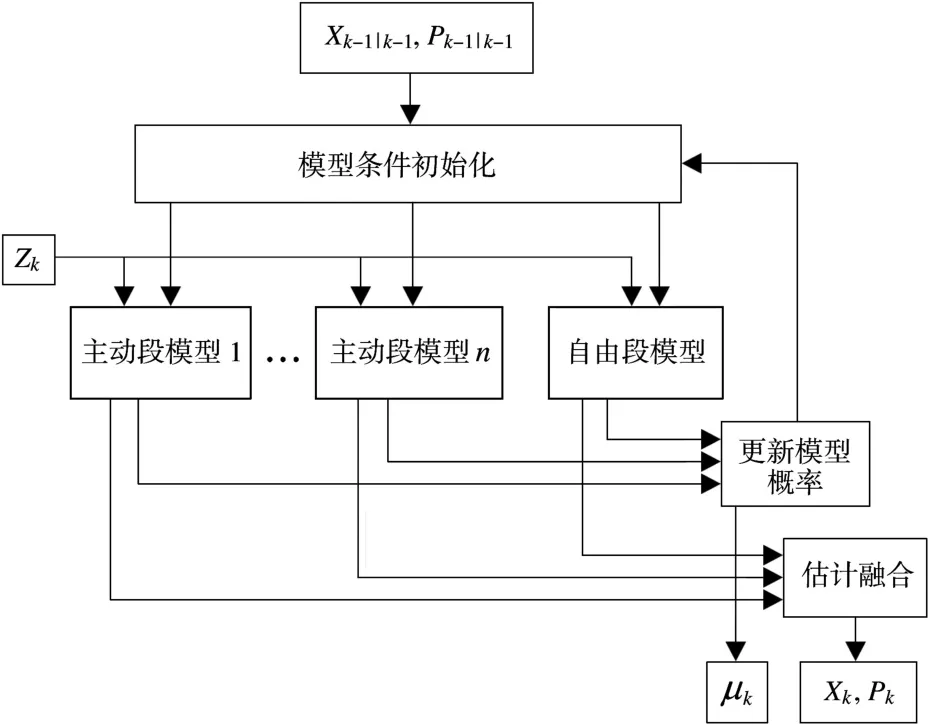
图2 弹道导弹主动段跟踪方法结构图

2.2 计算步骤

变结构多模型方法基于时变的模型集合,即跟踪系统根据模型的概率动态选择系统的跟踪模型。当判别导弹在主动段飞行时,目标具有推进力,模型集包含多个主动段模型和自由段模型;当判别导弹进入自由段后,将模型集中主动段模型删除。这种新的方法更适用于弹道导弹主动段的跟踪,它在跟踪精度和计算性能上都具有一定的优势。任一时刻,选定模型集后模型间的交互采用交互多模型(IM M)算法进行迭代滤波。

滤波算法的主要步骤包括:

第一步:模型条件初始化。

(1)计算模型混合概率

式中,πij为马尔可夫模型转移概率,给出了k-1时刻由模型Mjk-1到k时刻由模型Mik-1的转移概率,μik-1为k-1时刻模型Mik-1的概率,其中¯cj=

(2)按模型混合概率进行状态与协方差的初始化

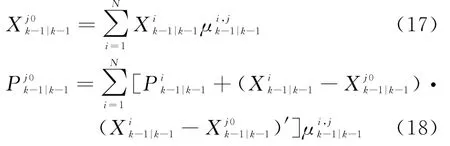
第二步:多模型采用卡尔曼的预测与更新。

(1)状态方程预测

(2)量测方程更新

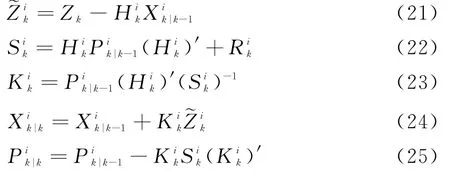
第三步:计算各模型的概率。

式中,c为归一化常数:

式中,Λik为在Gauss条件下的似然函数:

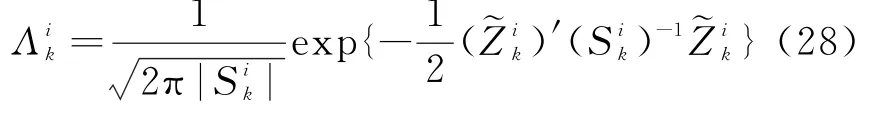
第四步:多模型进行状态估计融合。

计算k时刻,系统融合后的状态和误差协方差阵:

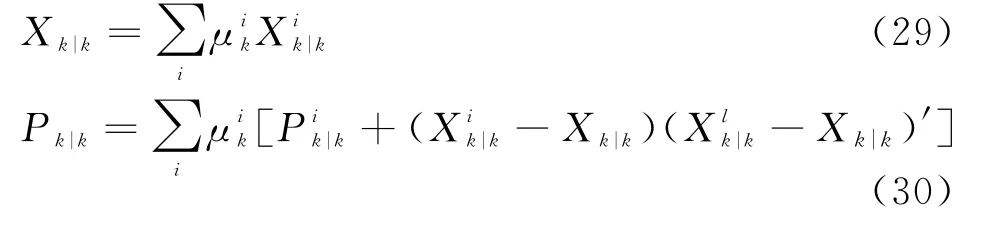
滤波器的输出是多个滤波器估计结果的加权平均值。

3 仿真分析

实验采用Matlab软件进行仿真,仿真产生的弹道导弹飞行轨迹经过坐标转换后,对飞行轨迹数据加入雷达量测噪声,雷达距离量测精度为100 m,方位和俯仰的量测精度均为0.1°,跟踪数据率为1 Hz,发现概率为1。采用蒙特卡罗仿真(独立运行100次)方法进行对比分析。

3.1 仿真场景1

仿真一级助推段的弹道导弹,其参数如下:飞行射程约为4 000 km,飞行时间为1 154 s,飞行最大高度为789.45 km,弹道系数为6 116;雷达站位置距发射点距离为195 km,关机点时间为80.25 s;假设跟踪时间为0～200 s,雷达站距跟踪第一点距离为195 km。

图3显示了导弹飞行时间与高度的变化,图4为导弹飞行时间与其加速度的变化,可以看出导弹在关机点前后加速度产生突变。算法在主动段跟踪时,本文算法中各跟踪模型的概率变化如图5所示。当弹道导弹处于主动段飞行时,即时间小于80 s时,主动段模型的概率最大,近似于1。当弹道导弹处于自由段飞行时,即时间大于80 s时,自由段模型的概率最大,近似于1。图5中的黑色虚线清晰地划分出飞行阶段的转换时刻,也即目标关机时刻的估计值。

图3 导弹高度随飞行时间的变化

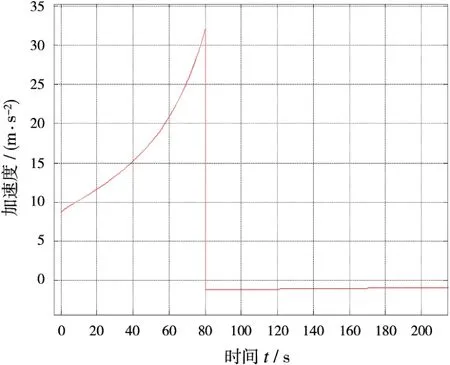
图4 导弹加速度随时间的变化

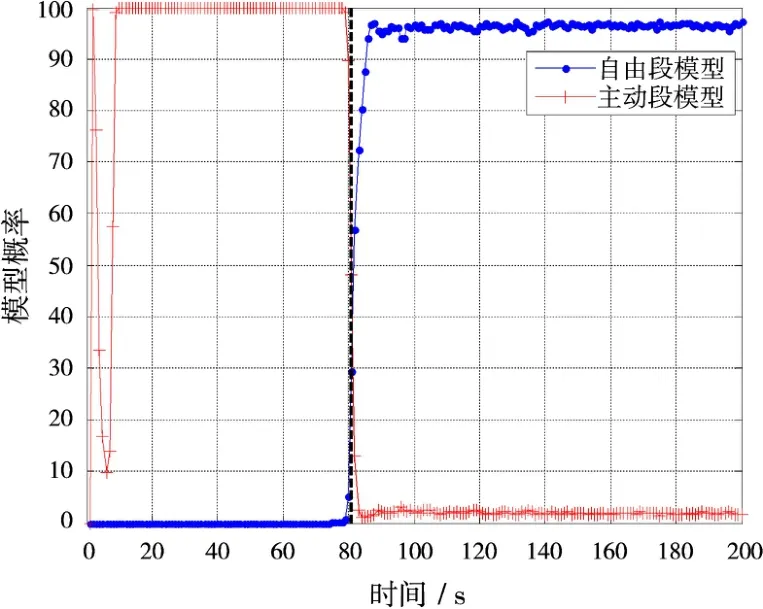
图5 算法中各模型的概率的变化

从表1可以看出,本文算法滤波后估计的位置误差是测量误差的27.9%;与单模型的EKF算法相比较,位置误差是EKF误差的32.6%,速度误差是EKF误差的21.1%。

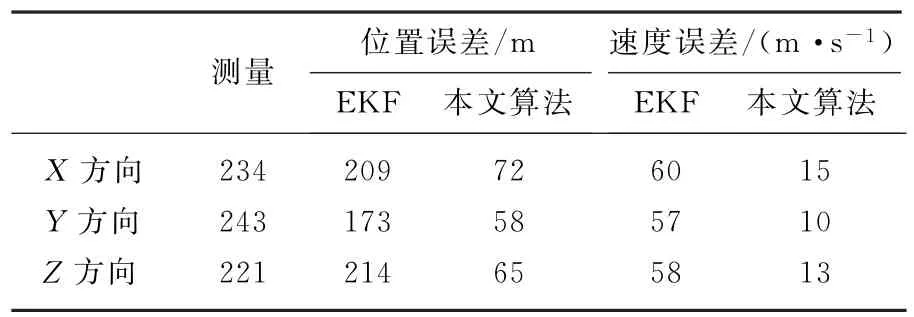
表1 主动段跟踪的均方根误差对比

3.2 仿真场景2

仿真含二级助推段的弹道导弹,其参数如下:飞行射程约为4 060 km,飞行时间为1 278 s,飞行最大高度为1 023 km,弹道系数为6 116;雷达站位置距发射点距离为195 km,一次助推关机点时间为41.129 s,二次助推关机点时间为183.829 s;假设跟踪时间为0～240 s,雷达站距跟踪第一点距离为195 km。

图6显示了弹道导弹加速度随时间变化的曲线。通过图7中模型概率的变化可以看出,本文的方法可以精确地估计出弹道导弹各级助推段关机点的时刻,一级关机时刻41 s,二级关机时刻184 s,可看出方法对目标关机时刻的估计精确到秒量级。

图6 导弹加速度随时间的变化

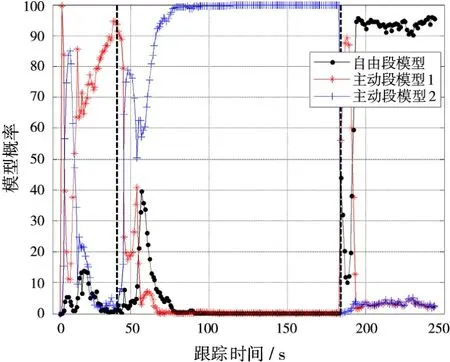
图7 算法中各模型的概率的变化

4 结束语

对弹道导弹主动段跟踪,并进行拦截,这是反导防御体系中前置地基雷达需要完成的最重要工作。目前,现有的导弹主动段跟踪方法在建模和跟踪性能上存在一些不足,本文提出一种新的可变结构多模型的导弹主动段跟踪方法,该方法具有以下的优势:1)针对传统基于单模型的方法,本文方法采用变结构多模型,对导弹主动段运动模型具有更好的性能;2)采用UKF非线性滤波方法,与传统的EKF跟踪算法会引入线性化的误差,它具有更好的滤波精度;3)通过模型集中模型概率的变化,可精确估计出导弹目标在主动段中各级助推段关机的时间。通过仿真实验看出,本文的方法明显提高了跟踪的精度,尤其是可精确估计导弹关机的时间,这对于估计导弹的关机点参数,以及之后自由段的精密跟踪具有非常重要的意义。今后的工作重点在于对本文方法进行工程应用和实际验证,并对算法的计算性能进行优化。

[1]BLACKMAN S,POPOLI R.Design and Analysis of Modern Tracking Systems[M].Norwood,MA:Artech House,1999.

[2]ZARCHAN P.Tactical and Strategic Missile Guidance[M].3rd ed.Reston,VA:AIAA,1997.

[3]LI X R,JILKOV V P.Survey of Maneuvering Target Tracking.Part II:Motion Models of Ballistic and Space Targets[J].IEEE Trans on Aerospace and Electronic Systems,2010,46(1):96-119.

[4]EASTHOPE P F,HEYS N W.A Multiple-Model Target-Oriented Tracking System[C]∥Signal and Data Processing of Small Target,Bellingham,WA:SPIE,1994:624-635.

[5]FARRELL W J.Interacting Multiple Model Filter for Tactical Ballistic Missile Tracking[J].IEEE Trans on Aerospace and Electronic Systems,2008,44(2):418-426.

[6]张涛,安玮,周一宇,等.基于推力加速度模板的主动段弹道跟踪方法[J].宇航学报,2006,27(3):385-389.

[7]钮俊清,单奇.多级助推段弹道导弹的轨迹仿真[J].雷达科学与技术,2011,9(2):144-149.

NIU Junqing,SHAN Qi.Trajectory Simulation of Ballistic Missile with Multi-Stage Boosters[J].Radar Science and Technology,2011,9(2):144-149.(in Chinese)

[8]BENAVOLI A,CHISCI L,FARINA A.Tracking of a Ballistic Missile with A-Priori Information[J].IEEE Trans on Aerospace and Electronic Systems,2007,43(3):1000-1016.

[9]钮俊清,单奇,任清安,等.跟踪弹道导弹全阶段的可变多模型方法[J].雷达科学与技术,2011,9(3):224-231.

NIU Junqing,SHAN Qi,REN Qingan,et al.A New Algorithm with Variable-Structure Multiple Model for Tracking Ballistic Missile at Entire Flight Stages[J].Radar Science and Technology,2011,9(3):224-231.(in Chinese)

[10]LI X R,JILKOV V P.Survey of Maneuvering Target Tracking.Part V:Multiple-Model Methods[J].IEEE Trans on Aerospace and Electronic Systems,2005,41(4):1255-1321.

[11]MAZOR E,AVERBUCH A,BAT-SHALOM Y,et al.Interacting Multiple Model Methods in Target Tracking:A Survey[J].IEEE Trans on Aerospace and Electronic Systems,1998,34(1):103-123.

[12]FARINA A,RISTIC B,BENVENUTI D.Tracking a Ballistic Target:Comparison of Several Nonlinear Filters[J].IEEE Trans on Aerospace and Electronic Systems,2002,38(3):854-867.

[13]JULIER S J,UHLMANN J K,DURRANTWHYTE H F.A New Approach for Filtering Nonlinear Systems[C]∥1995 American Control Conference,Seattle,WA:IEEE,1995:1628-1632.

[14]JULIER S J,UHLMANN J K.Unscented Filtering and Nonlinear Estimation[J].Proceedings of the IEEE,2004,92(3):401-422.